
第三节四叉树 假定一个平面图形是黑白的二值图形, 即组成图形象素阵列的仅有黑色象素值1,白 色象素值0,设表现图形的象素阵列由2n×2” 个象素组成。 表示该图形的四叉树结构可以如下形成: 图形显然包括2nX2的正方形中,这个正方 形是四叉树的根结点。 若图形整个地占据这个正方形,则图形 就用该正方形表示,否则将该正方形均分为 四个小正方形,每个小正方形边长为原正方 形边长的一半.它们是根结点的四个子结点, 可编号为0,1,2,3
第三节 四叉树 假定一个平面图形是黑白的二值图形, 即组成图形象素阵列的仅有黑色象素值1,白 色象素值0,设表现图形的象素阵列由2 n×2 n 个象素组成。 表示该图形的四叉树结构可以如下形成: 图形显然包括2 n×2 n的正方形中,这个正方 形是四叉树的根结点。 若图形整个地占据这个正方形,则图形 就用该正方形表示,否则将该正方形均分为 四个小正方形,每个小正方形边长为原正方 形边长的一半.它们是根结点的四个子结点, 可编号为0,1,2,3

再考查每个小正方形,若整个被图 形占据,则标记相应结点为1,可称为黑 结点。若整个与图形不相交,则标记相 应结点为0,可称为白结点。 若不是上述两情形,即与图形部分 相交,则称相应结点是灰结点并将其一 分为四。当再分生成小正方形边长达到 一个象素单位时,再分终止,此时一般 应将仍是灰结点的改为黑结点,如此形 成了平面图形的四叉树表示
再考查每个小正方形,若整个被图 形占据,则标记相应结点为1,可称为黑 结点。若整个与图形不相交,则标记相 应结点为0,可称为白结点。 若不是上述两情形,即与图形部分 相交,则称相应结点是灰结点并将其一 分为四。当再分生成小正方形边长达到 一个象素单位时,再分终止,此时一般 应将仍是灰结点的改为黑结点,如此形 成了平面图形的四叉树表示
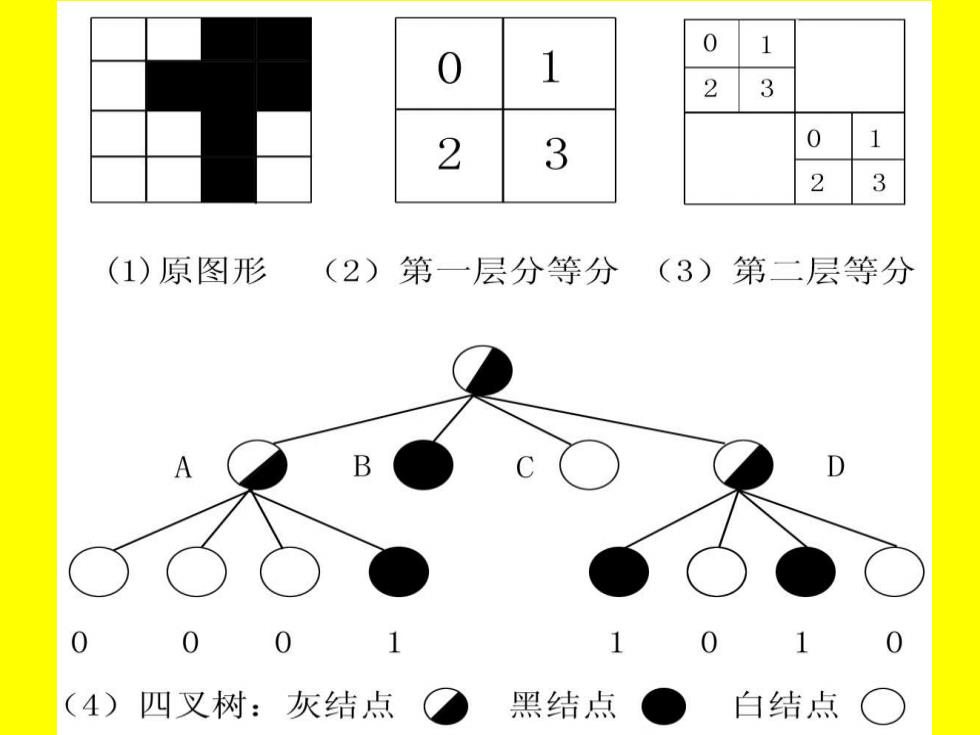
0 2 3 2 3 0 2 3 (1)原图形 (2)第一层分等分 (3)第二层等分 1 1 (4)四叉树:灰结点 黑结点 白结点

四叉树的存储结构,即规则方式、线 性方式和一对四方式,相应的四叉树也就 称为规则四叉树、线性四叉树和一对四式 四叉树。 规则四叉树是用五个字段的记录来表 示树中的每个结点,其中一个用来描述结 点的特性,即是灰、黑、白三类结点中的 哪一种。其余四个用于存放指向四个子结 点的指针。 线性四叉树以某一预先确定的次序遍 历四叉树形成一个线性表结构 RA'abcdBCD'efgh。其中R表示根,字母 右上角加'表示是灰结点
四叉树的存储结构,即规则方式、线 性方式和一对四方式,相应的四叉树也就 称为规则四叉树、线性四叉树和一对四式 四叉树。 规则四叉树是用五个字段的记录来表 示树中的每个结点,其中一个用来描述结 点的特性,即是灰、黑、白三类结点中的 哪一种。其余四个用于存放指向四个子结 点的指针。 线性四叉树以某一预先确定的次序遍 历四叉树形成一个线性表结构 。 RA’abcdBCD’efgh。其中R表示根,字母 右上角加’表示是灰结点

一对四式四叉树的存储结构每个结 点有五个字段,其中四个字段用来描述该 结点的四个子结点的状态,另一个结点存 放指向子结点记录存放处的指针。四个子 结点对应的记录是依次连续存放的。 0 1 2 3
一对四式四叉树的存储结构 每个结 点有五个字段,其中四个字段用来描述该 结点的四个子结点的状态,另一个结点存 放指向子结点记录存放处的指针。四个子 结点对应的记录是依次连续存放的

灰 黑 白灰 灰 黑 白 灰 R 白 白 白 灰 白 白 白 灰 A 黑 白黑白 D 黑 白 黑 白 为节省存贮空间,有两个途径可以采取。 一个是增加计算量;另一个途径是在记录中 再增加一个字节,一分为四,每个子结点对应2 位,表示它的子结点在指针指向区域中的偏移
为节省存贮空间,有两个途径可以采取。 一个是增加计算量;另一个途径是在记录中 再增加一个字节,一分为四,每个子结点对应2 位,表示它的子结点在指针指向区域中的偏移

第四节三维几何模型 ·几何元素 形体的模型主要指的就是包含图形信 息所形成的模型。 形体本身的构造有一定的层次性,低 层部分组合构成上一层部分,而上一层部 分组合又可以构成更高一层的部分,依此 类推可形成多层结构。其中,每一层中的 部分,我们把它有称为几何元素
第四节 三维几何模型 • 几何元素 形体的模型主要指的就是包含图形信 息所形成的模型。 形体本身的构造有一定的层次性,低 层部分组合构成上一层部分,而上一层部 分组合又可以构成更高一层的部分,依此 类推可形成多层结构。其中,每一层中的 部分,我们把它有称为几何元素

点 它是0维几何元素,有端点、交点、切 点、孤立点等形式。 曲线、曲面的应用中会涉及到三种类型 的点: 型值点相应曲线、曲面必然经过的点。 控制点相应曲线、曲面不一定经过的点,仅 用于确定位置和形状。 插值点在型值点之间插入的一系列点,用于 提高曲线曲面的输出精度
点 它是0维几何元素,有端点、交点、切 点、孤立点等形式。 曲线、曲面的应用中会涉及到三种类型 的点: 型值点 相应曲线、曲面必然经过的点。 控制点 相应曲线、曲面不一定经过的点,仅 用于确定位置和形状。 插值点 在型值点之间插入的一系列点,用于 提高曲线曲面的输出精度

不同的空间中点的表示方式 一维空间中用一元组{t}表示; 二维空间中用二元组{x,y或{x(t),y(t)} 表示; 三维空间中用三元组{x,y,z}或 {x(t),y(t),z(t)}表示; 点是几何造型中的最基本的元素,曲线、 曲面和其它形体都可以用有序的点集描述。 用计算机存储、管理、输出形体的实质 就是对点集及其连接关系的处理
不同的空间中点的表示方式 一维空间中用一元组{t}表示; 二维空间中用二元组{x,y}或{x(t),y(t)} 表示; 三维空间中用三元组{x,y,z}或 {x(t),y(t),z(t)}表示; 点是几何造型中的最基本的元素,曲线、 曲面和其它形体都可以用有序的点集描述。 用计算机存储、管理、输出形体的实质 就是对点集及其连接关系的处理

边 边是一维几何元素,是两个邻面(正则形 体)或多个邻面(非正则形体)的交界。边分 直线边和曲线边。直线边由起点和终点两端点 确定;曲线边由一系列型值点或控制点表示, 也可以用显示、隐式方程描述。 环 环是有序有向边(直线段或曲线段)组 成的面的封闭边界。环中的边不能相交,相邻 两条边共享一个端点。环有内外之分,确定面 的最大外边界的环称之为外环,通常其边按逆 时针方向排序。而把确定面中内孔或凸台边界 的环称之为内环,其边相应外环排序方向相反, 通常按顺时针方向排序
边 边是一维几何元素,是两个邻面(正则形 体)或多个邻面(非正则形体)的交界。边分 直线边和曲线边。直线边由起点和终点两端点 确定;曲线边由一系列型值点或控制点表示, 也可以用显示、隐式方程描述。 环 环是有序有向边(直线段或曲线段)组 成的面的封闭边界。环中的边不能相交,相邻 两条边共享一个端点。环有内外之分,确定面 的最大外边界的环称之为外环,通常其边按逆 时针方向排序。而把确定面中内孔或凸台边界 的环称之为内环,其边相应外环排序方向相反, 通常按顺时针方向排序