
上述结果对任意的成立,令0,可写 出四个B样条函数: 0,40-61-3 N1,4u)(3u3-6u2+4) N2,4合-33323u+1) N,4=63
上述结果对任意的i成立,令i=0,可写 出四个B样条函数: 3 u 6 1 (u) 3,4 N 3 u 1 ) 2 3 u 3 ( 3 u 6 1 (u) 2,4 N 4 ) 2 6 u 3 (3u 6 1 (u) 1,4 N 3 ( 1 u ) 6 1 (u) 0,4 N = = − + + + = − + = −

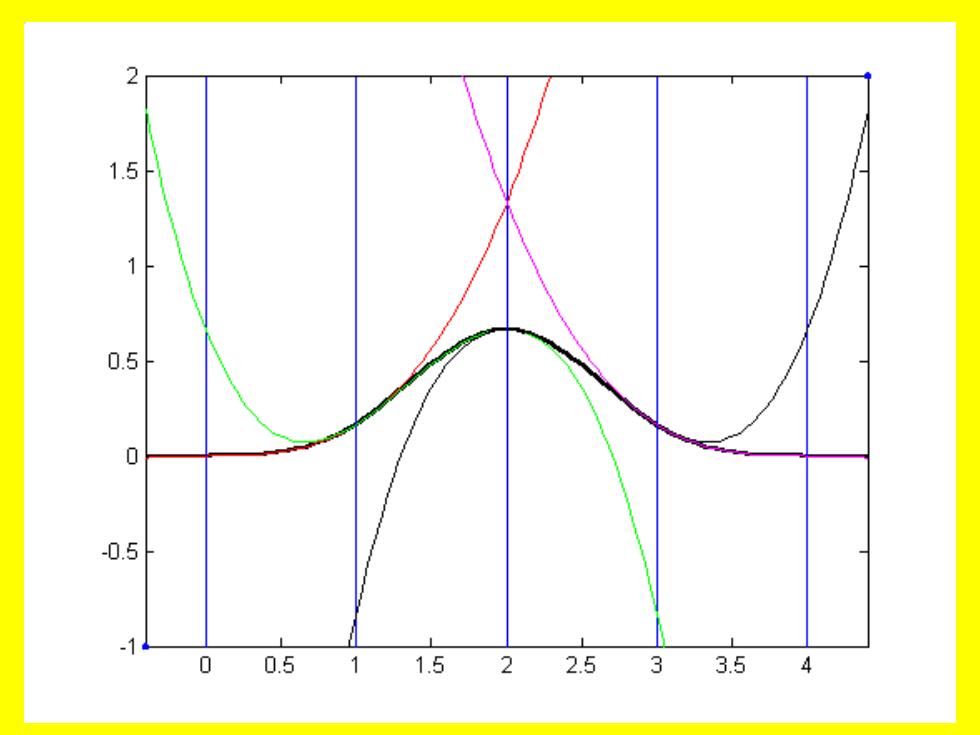
由节点向量(0,1,2,3,4)所确 定的均匀B样条基函数W:4()曲线 (=0,1,2,3)。图所示的B样条 基函数W4()由四条三次多项式 曲线片拼接而成。当节点在区间 [uu4k小上B样条曲线基函数Wk() 大于0,而在其它区间上则为0, 并且W,k()在节点(upu+1, u+k)处是连续的
由节点向量(0,1,2,3,4)所确 定的均匀B样条基函数Ni,4(u)曲线 (i=0,1,2,3)。图所示的B样条 基函数Ni,4(u)由四条三次多项式 曲线片拼接而成。当节点在区间 [ui ,ui+k ]上B样条曲线基函数Ni,k (u) 大于0,而在其它区间上则为0, 并且Ni,k (u)在节点(ui , ui+1,…, ui+k)处是连续的
2 1.5 0.5 0 -0.5 0 0.5 1 1.5 22.5 3 3.5

设给出t1个控制点Po,P1,) Pn2 则所确定的4阶3次等距B样条 曲线是: P(0=0:@ ∑N.(u)P j= 0≤u≤1,i=0,1,…,n-3
设给出n+1个控制点P0,P1,…, Pn,则所确定的4阶3次等距B样条 曲线是: 0 u 1 ,i 0,1, ,n 3 N (u) P , 3 j 0 (u) i P(u) Q j,4 i j = − = = = +
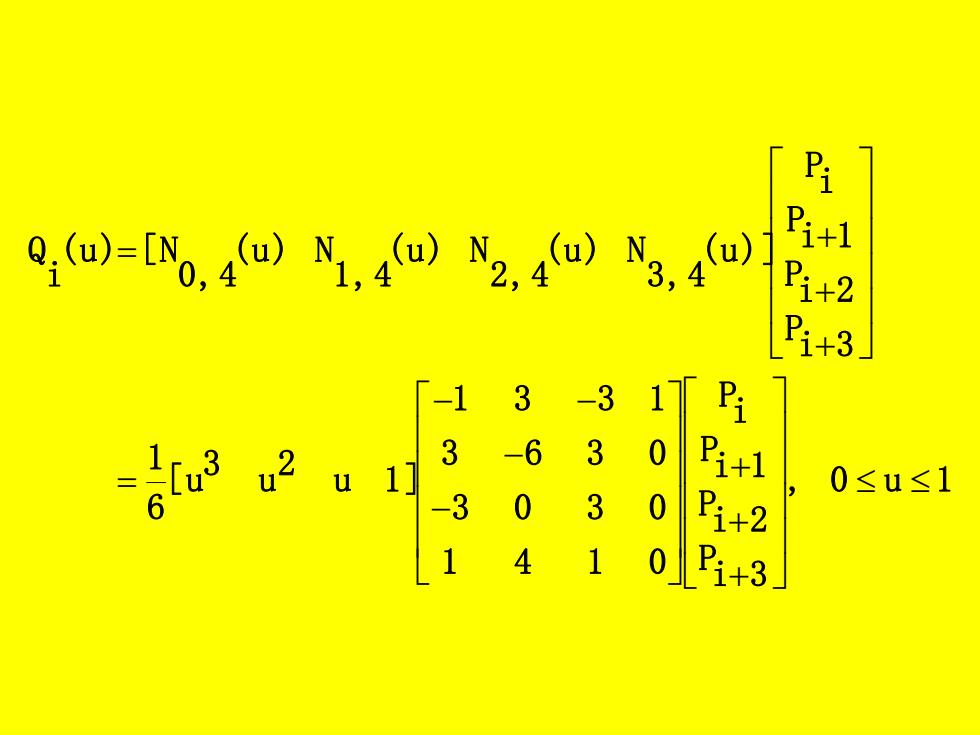
0:6a)=[%,4@)N,40N2,4@)N3,4@ i+ +2 B+ -1 3 -3 1 -6 3 0 -3 Pi+1 0 0≤u≤1 0 Pi+2 L1410+3
, 0 u 1 i 3 P i 2 P i 1 P i P 1 4 1 0 3 0 3 0 3 6 3 0 1 3 3 1 u 1 ] 2 u 3 [ u 6 1 i 3 P i 2 P i 1 P i P (u)] 3,4 (u) N 2,4 (u) N 1,4 (u) N 0,4 (u) [ N i Q + + + − − − − = + + + =
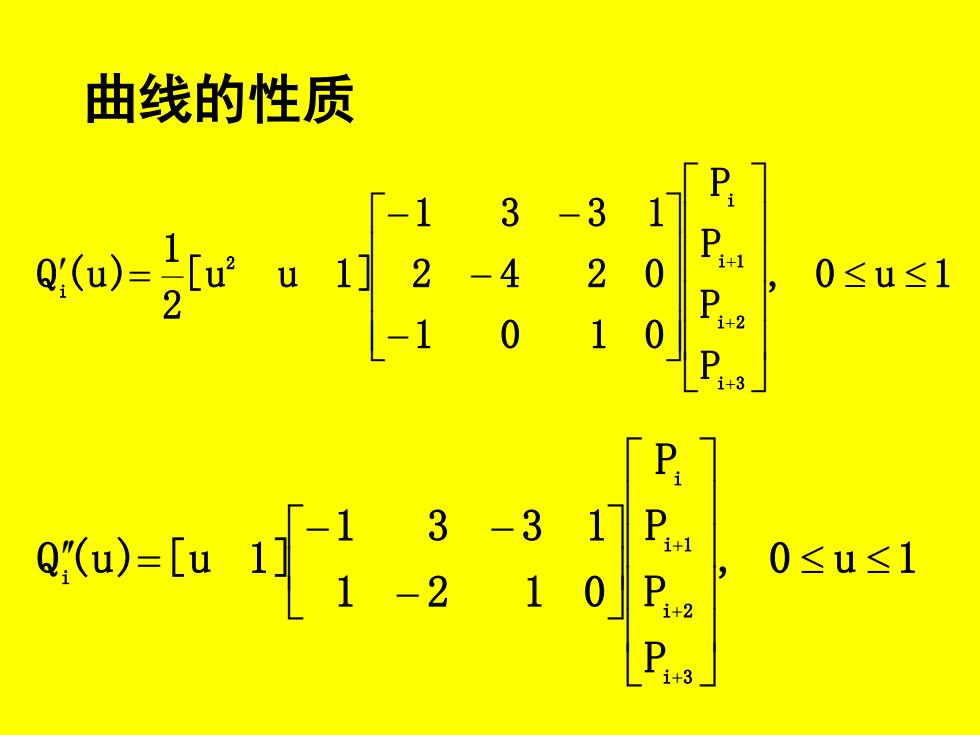
曲线的性质 日 3 -3 17 2 0≤u≤1 010 ca-6 P 0≤u≤1 D i+3
曲线的性质 , 0 u 1 P P P P 0 0 1 1 2 3 0 4 3 1 2 1 [ u u 1 ] 2 1 Q (u) i 3 i 2 i 1 i 2 i − − − − = + + + , 0 u 1 P P P P 0 1 1 3 2 3 1 1 Q (u) [ u 1 ] i 3 i 2 i 1 i i − − − = + + +
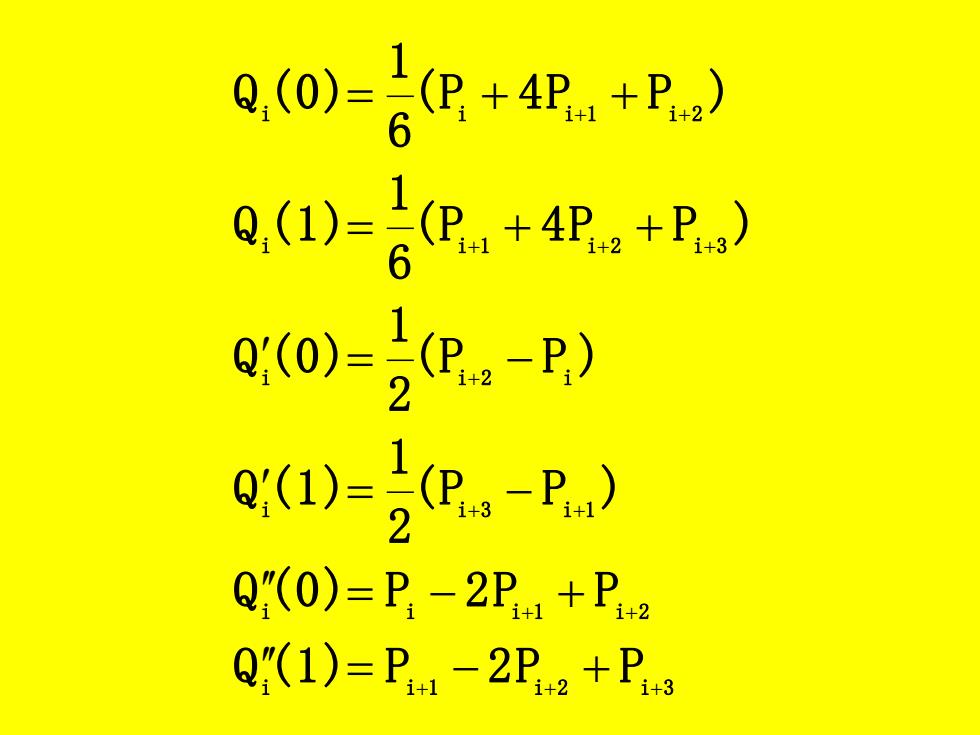
0o=6把+4e,+P,) Q,(1)=(P,+4P+Ps) Q(o)=2(P.-P) 2 Q(1)=(-P) 2 Q(0)=P-2P1+P2 Q(1)=P1-2P2+Pg
i i 1 i 2 i 3 i i i 1 i 2 i i 3 i 1 i i 2 i i i 1 i 2 i 3 i i i 1 i 2 Q (1) P 2 P P Q (0) P 2 P P ( P P ) 2 1 Q (1) ( P P ) 2 1 Q (0) ( P 4 P P ) 6 1 Q (1) ( P 4 P P ) 6 1 Q (0) + + + + + + + + + + + + + = − + = − + = − = − = + + = + +
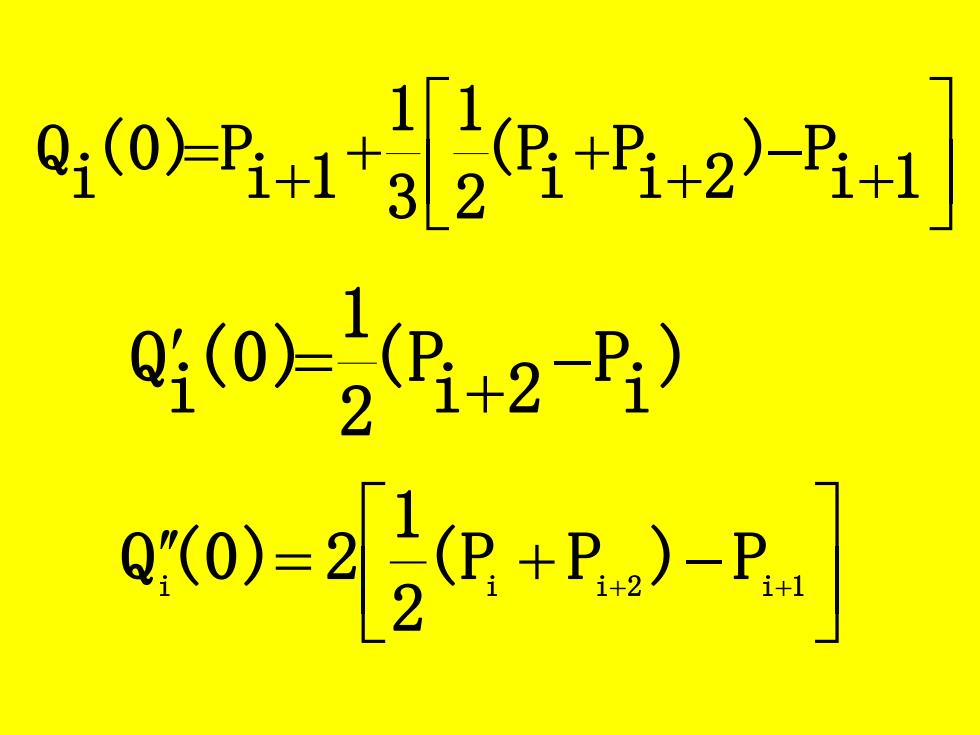
0《@-生1+24+2-+1 g4o-42 o=2+R)-e]
+ − + + + + = i 1 ) P i 2 P i ( P 2 1 3 1 i 1 (0) P i Q i = ( Pi + Pi+2 )− Pi+1 2 1 Q (0) 2 ) i P i 2 ( P 2 1 (0) i Q − + =
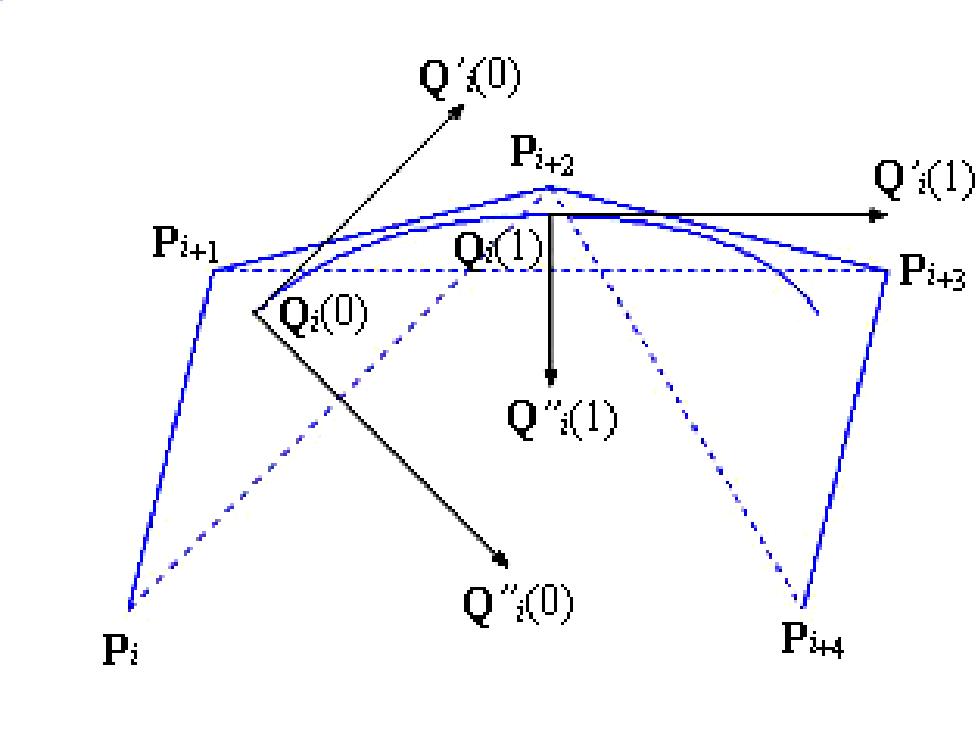
Q0) P:+3 Q〔1) Pi+3 Q(1) Q0) P Pi4

P,P+13P2,P4确定的一段曲线的 起点的位置向量、切线向量及二阶导向量, 事实上都只与△PP4P2有关,而终点处各 量只与△PP42P3,有关。如果考虑接下 去的一段曲线,即P1,P2,P3,P4确定 的一段,在其起点,上述各量就只与 P+P2P有关,并恰好是前一段曲线终点 处的上述各量,自然是对应相等的。这就证 明了曲线在拚接处是连续的,一阶和二阶导 数也是连续的。因此知道4阶3次等距B样条 曲线:虽然分段确定,但各段拚接处有直到 二阶导数的连续性,整条曲线是光滑的
Pi,Pi+1,Pi+2,Pi+3确定的一段曲线的 起点的位置向量、切线向量及二阶导向量, 事实上都只与ΔPi Pi+1Pi+2有关,而终点处各 量只与ΔPi+1Pi+2Pi+3,有关。如果考虑接下 去的一段曲线,即Pi+1,Pi+2,Pi+3,Pi+4确定 的一段,在其起点,上述各量就只与 Pi+1Pi+2Pi+3有关,并恰好是前一段曲线终点 处的上述各量,自然是对应相等的。这就证 明了曲线在拚接处是连续的,一阶和二阶导 数也是连续的。因此知道4阶3次等距B样条 曲线:虽然分段确定,但各段拚接处有直到 二阶导数的连续性,整条曲线是光滑的