吉林大学：《计算机图形学》课程电子教案（PPT课件）第四章 曲线和曲面 第四节 Bezier曲线和曲面

指定四个角点以及在这些 点上的切向量和扭曲向量后， 求解曲面的表达式。 已知角点位置向量00,10 以及在这两点关于u的切向量 O0,和01，可以用Hermite插值 公式来指定一条边界线：

指定四个角点以及在这些 点上的切向量和扭曲向量后， 求解曲面的表达式。 已知角点位置向量00，10 以及在这两点关于u的切向量 00u和01u，可以用Hermite插值 公式来指定一条u边界线：

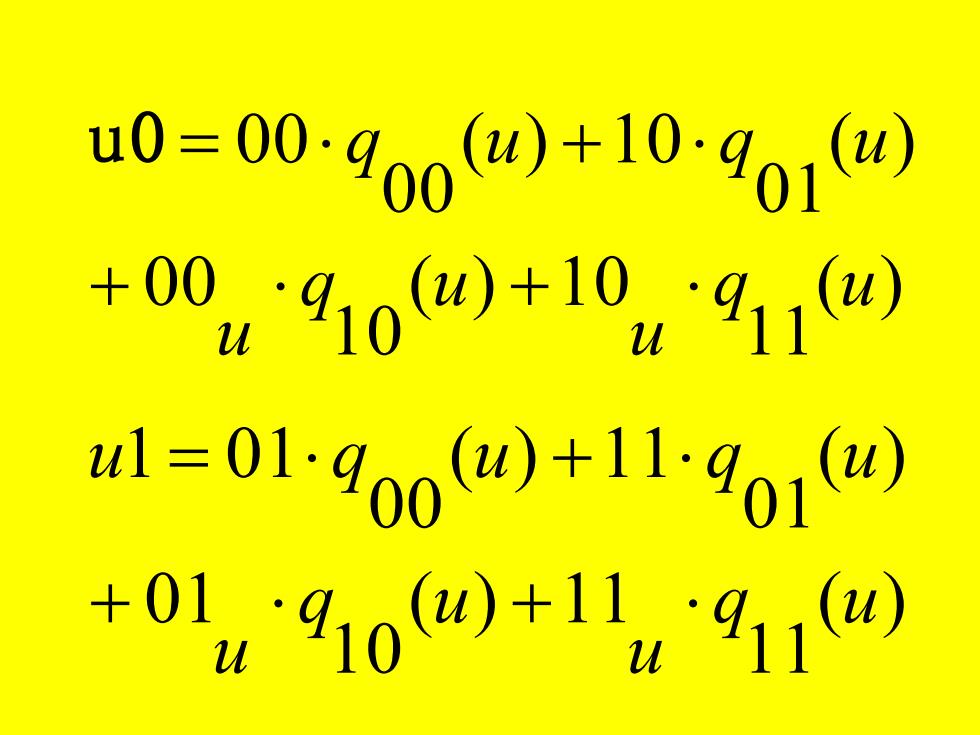
a0=00~400am+10-901（0） +00u9100）+104911（m U w1=01~900④)+11901w） +0149100+1l4911@

( ) 11 ( ) 10 10 00 ( ) 01 ( ) 10 00 00 q u u q u u q u q u +  +  u 0 =  +  ( ) 11 ( ) 11 10 01 ( ) 01 ( ) 11 00 1 01 q u u q u u u q u q u +  +  =  + 

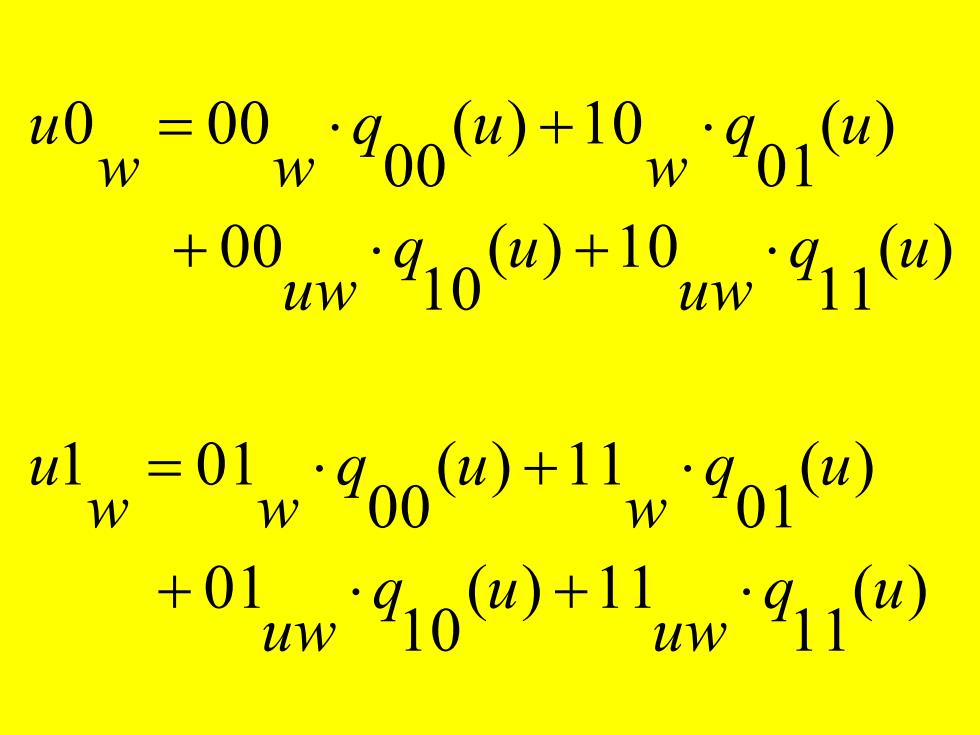
u0 =00w900四）+10w9010 W +00u910@）+10w910 nl.=01w400 W W 四+1lw901四 +0l4w910a+1l4w910

( ) 1 1 ( ) 1 1 1 0 0 1 ( ) 0 1 ( ) 1 1 0 0 1 0 1 ( ) 1 1 ( ) 1 0 1 0 0 0 ( ) 0 1 ( ) 1 0 0 0 0 0 0 q u uw q u uw q u w q u w w u q u uw q u uw q u w q u w w u +  +  =  +  +  +  =  + 

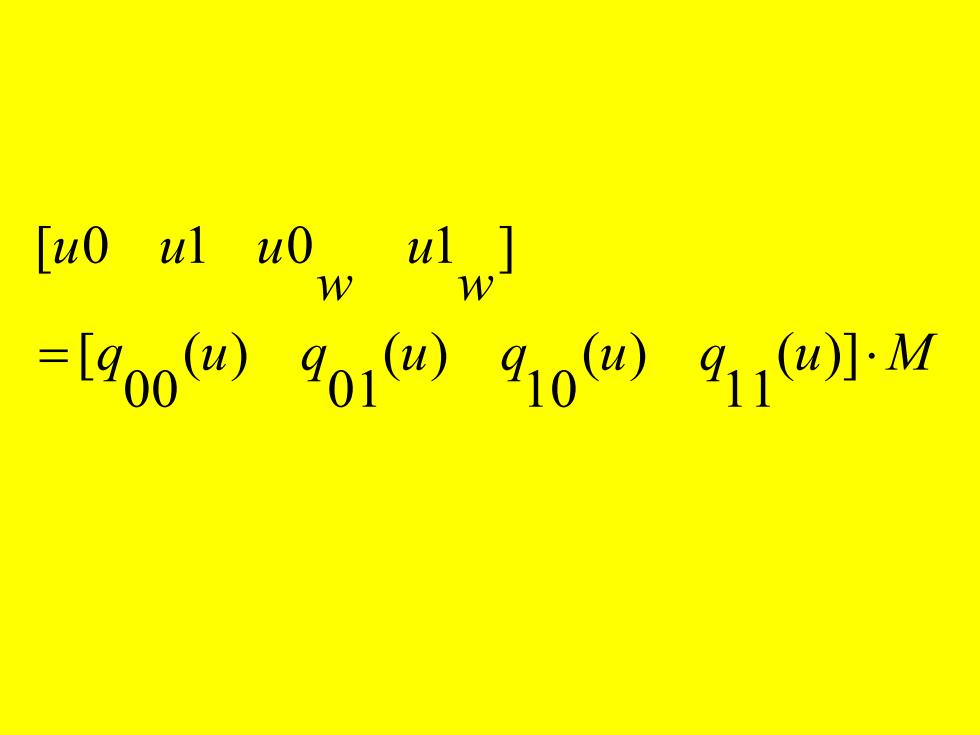
[uO ul uO ul W W =[900四）9o1(）9100）411w]1M

q u q u q u q u M w u w u u u = ( )] 11 ( ) 10 ( ) 01 ( ) 00 [ [ 0 1 0 1 ]

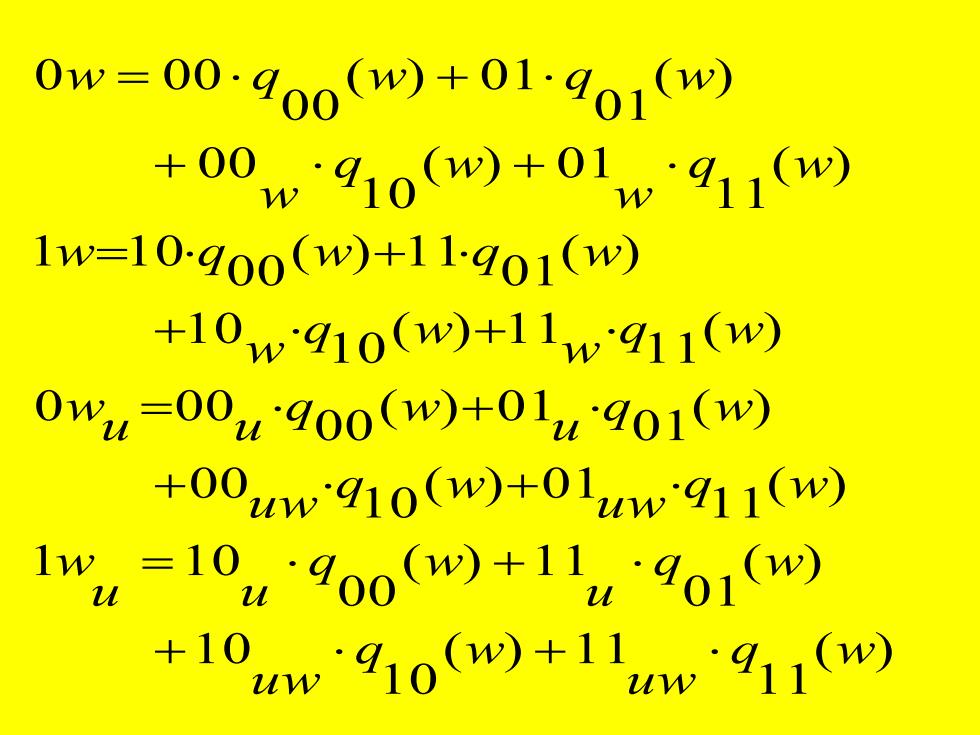
0w=00.900(w)+01~401(w +00w910w+01w911w) 1w=10-900(w)+11·901(w) +10w910(w)+11w911(w) 0wu=00u900(w+01u901(w) +00zuw910(w)+01uw911(w) 1w4=10u·go0w）+114901w +104w910w)+1uw911w)

( ) 1 1 ( ) 1 1 1 0 1 0 ( ) 0 1 ( ) 1 1 0 0 1 1 0 ( ) 1 1 ( ) 0 1 1 0 0 0 ( ) 0 1 ( ) 0 1 0 0 0 0 0 ( ) 1 1 ( ) 1 1 1 0 1 0 ( ) 0 1 ( ) 1 1 0 0 1 1 0 ( ) 1 1 ( ) 0 1 1 0 0 0 ( ) 0 1 ( ) 0 1 0 0 0 0 0 q w uw q w uw q w u q w u u w q w uw q w uw q w u q w u u w q w w q w w w q w q w q w w q w w w q w q w +  +  =  +  +  +  =  +  +  +  =  +  +  +  =  + 

=M. 将上两式代入前式，就可以得到：

            =                ( ) 11 ( ) 10 ( ) 01 ( ) 00 1 0 1 0 q w q w q w q w M u w u w w w 将上两式代入前式，就可以得到：

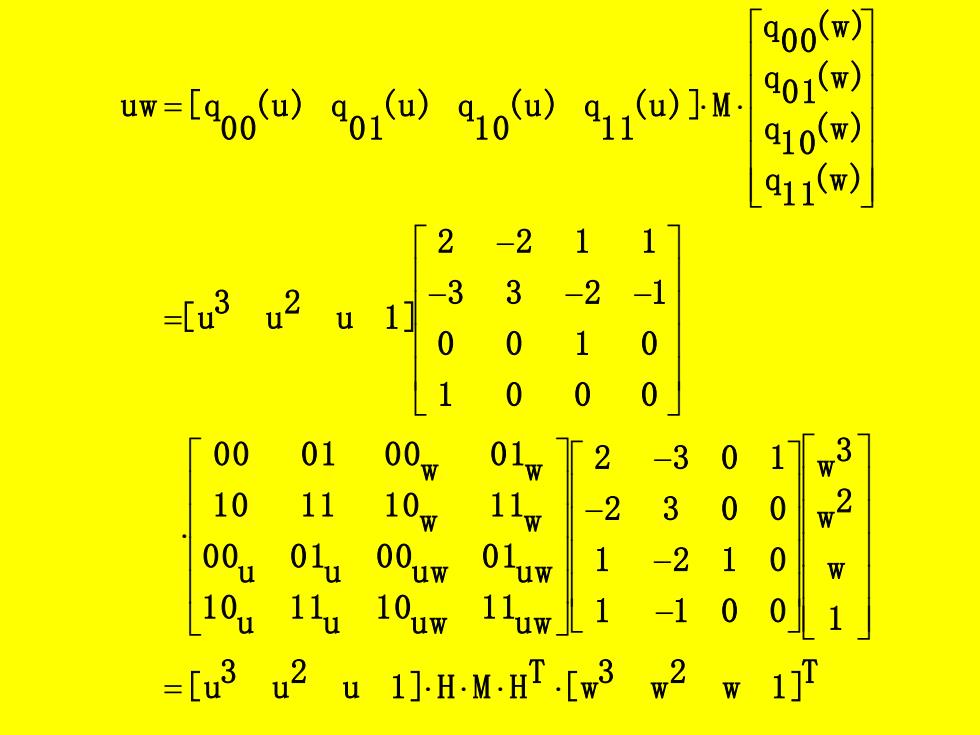
00m） um=[0uW91@）910o)9110)]-M 01(w) g10w) 911) 2 -2 1 1 -[u3 u2 u1 -3 3 -2 -1 0 0 0 0 0 0 60004 01 00 01w 2 -3 1 3 10w 11w -2 0 2 0 1 1Ouw 11u 0 1 =-[u3 u 1]-HMH.[w3 w2 7171

T w 1 ] 2 w 3 [ w T u 1 ] H M H 2 u 3 [ u 1 w 2 w 3 w 1 1 0 0 1 2 1 0 2 3 0 0 2 3 0 1 u w 1 1 u w 1 0 u 1 1 u 1 0 u w 0 1 u w 0 0 u 0 1 u 0 0 w 1 1 w 1 0 1 1 1 0 w 0 1 w 0 0 0 1 0 0 1 0 0 0 0 0 1 0 3 3 2 1 2 2 1 1 u 1 ] 2 u 3 [ u (w) 1 1 q (w) 1 0 q (w) 0 1 q (w) 0 0 q (u)] M 1 1 (u) q 1 0 (u) q 0 1 (u) q 0 0 u w [ q =                               − − − −                          − − − − =               =  

给出四个角点以及在该角点上的切向量和扭 曲向量来构造Coons曲面表达式。设在平面上有 四点PoP1,P2,P3,它们的位置向量分别为(0， 0,0),(0,0.75,0),(0.75,0,0),(0.75, 0.75,0)。该四点的切向量、跨界切向量和扭 曲向量，定义在关于角点的信息矩阵仲： 0 3 4

给出四个角点以及在该角点上的切向量和扭 曲向量来构造Coons曲面表达式。设在平面上有 四点P0，Pl，P2，P3，它们的位置向量分别为(0， 0，0)，(0，0.75，0)，(0.75，0，0)，(0.75， 0.75，0)。该四点的切向量、跨界切向量和扭 曲向量，定义在关于角点的信息矩阵M中：             − − − − − =  1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 4 3 x M

3 0 M 4 3 M Z 4

            − − =              − − − − =  0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 4 3 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 4 3 z M y M

3-3 0 0 7「3 x(u,w)=[u3 u2 u 4.53.750.75 0 1 w2 00.75-0.750.75 00.75-0.75 0 1 0 0 0 w3 y(u,m）-[u3u2u1 -0.750.75 -0.75 2 0 0.75-0.75 0.75 W 00 0.75 1 0 0 0 0 03 z(u,)=[u3u2u1 -0.750.75 0 u∈[0,1]，w∈[0,1 0 0.75-0.750 1.5-2.250.75 0 1

u [0,1],w [0,1] 1 w 2 w 3 w 1.5 2.25 0.75 0 0 0.75 0.75 0 0 0.75 0.75 0 0 0 0 0 u 1 ] 2 u 3 z(u,w ) [ u 1 w 2 w 3 w 0 0 0.75 0 0 0.75 0.75 0.75 0 0.75 0.75 0.75 0 0 0 0 u 1 ] 2 u 3 y(u,w ) [ u 1 w 2 w 3 w 0 0.75 0.75 0 0 0.75 0.75 0.75 4.5 3.75 0.75 0 3 3 0 0 u 1 ] 2 u 3 x(u,w ) [ u                             − − − =                           − − − =                           − − − − =