
若给出空间若干点的坐标 (x1,y1,z1),(x2,y2,z2),.(xn,ynzn), 注意这里没有要求这些点共面或围成了凸 多边形,都可以求出通过或接近这些点的 一个平面方程Ax+By+Cz+D=0: 是6y-y%+2 2i=1 B-,是么-+ 21=1
若给出空间若干点的坐标 (x1,y1,z1),(x2,y2,z2),….(xn,yn,zn), 注意这里没有要求这些点共面或围成了凸 多边形,都可以求出通过或接近这些点的 一个平面方程Ax+By+Cz+D=0: = = − + n i 1 ) j z i )(z j y i ( y 2 1 A = = − + n i 1 ) j x i )(x j z i ( z 2 1 B

1 C= (81-x)(y1+y时 211 D=-Ax1-By1-Cz1 式中若i=n,则j=1,否则j=i+1 平面方程的求交 A x+B y+C z+D=0 A2x+B2y+C2Z+D2=0
= = − + n i 1 ) j y i )(y j x i ( x 2 1 C D=-Ax1-By1-Cz1 式中若i=n,则j=1,否则j=i+1 平面方程的求交 A1 x+B1 y+C1 z+D1=0 A2 x+B2 y+C2 z+D2=0

A1 B1_C1 两平面重合或平行, A2 B2 一般算没有交点 分别对每个多边形表面各边相应 的线段,计算它与另一个多边形表面所 在平面的交点。注意这里是求线段与 平面的交点,即交点在线段延长线上时 算不相交。假定两个多边形表面都是 凸的,故共可以交出四个交点
2 C 1 C 2 B 1 B 2 A 1 A = = 两平面重合或平行, 一般算没有交点 分别对每个多边形表面各边相应 的线段,计算它与另一个多边形表面所 在平面的交点。注意这里是求线段与 平面的交点,即交点在线段延长线上时 算不相交。假定两个多边形表面都是 凸的,故共可以交出四个交点

线段与平面的交点计算 空间线段两个端点的坐标(x1,y1,z1)和 X2,y2,z2)给出,平面方程Ax+By+Cz+D=0。 x=x1+(x2-x1)t y=y1+(y2-y1)t z=z1+(z2-z1)t
线段与平面的交点计算 空间线段两个端点的坐标(x1,y1,z1)和 x2,y2,z2)给出,平面方程Ax +By+Cz+D=0。 = + − = + − = + − ) t 1 z 2 ( z 1 z z ) t 1 y 2 ( y 1 y y ) t 1 x 2 ( x 1 x x

代入平面方程,得: A(K1+(X2-x1)t)+B(y1+(y2-y1))+C(21+(亿2-Z)t)+D=0 整理得到: [A(X2-X)+B(y2-y+C(ZZ-(Ax+By+Cz+D) 于是知道,若 A(K2-X1+B(y2-y1+C(z2-z1)=0 则所给线段在平面上或与平面平行,没有唯一确 定的交点。否则,交点对应的参数可以求出: AX1+By1+CZ1+D A(x2x1)+B(y2y1)+C(z2z1)
代入平面方程,得: A(x1+(x2 -x1 )t)+B(y1+(y2 -y1 )t)+C(z1+(z2 -zl )t)+D=0 整理得到: [A(x2 -x1 )+B(y2 -y1 )+C(z2 -zl )]t=-(Ax1+By1+Cz1+D) 于是知道,若 A(x2 -x1 )+B(y2 -y1 )+C(z2 -z1 )=0 则所给线段在平面上或与平面平行,没有唯一确 定的交点。否则,交点对应的参数t可以求出: A(x2-x1) B(y2-y1) C(z2-z1) D 1 C z 1 B y 1 A x t + + + + + = −

第三节平面中的凸壳算法 凸壳包含一个平面点集的最小凸区域 凸区域指要求区域内任意两点的连 线仍在该区域内。 设S是平面上n个点的集合,则S的凸 壳是一个凸多边形,它包含所有n点且面 积最小。事实上求点集$的凸壳就是要在 S中选出壳上的点并排出围成凸多边形的 次序
第三节 平面中的凸壳算法 凸壳 包含一个平面点集的最小凸区域 凸区域指要求区域内任意两点的连 线仍在该区域内。 设S是平面上n个点的集合,则S的凸 壳是一个凸多边形,它包含所有n点且面 积最小。事实上求点集S的凸壳就是要在 S中选出壳上的点并排出围成凸多边形的 次序

Graham扫描算法 处理的思路是设想有一内点0并且不 妨设想0就是坐标原点,这时点集$中所有各 点相对轴0X有一个倾角。所有各点按倾角 递增排序后,如果某一点不是壳上顶点,则 它必然在两个壳顶点与点0形成的三角形内 部。 Grahamj扫描的实质是围绕已经按"倾 角"排序的各顶点进行一次扫描,在扫描过 程中消去在凸壳内部的点,留下以希望次序 排列的壳顶点
• Graham扫描算法 处理的思路是设想有一内点O并且不 妨设想O就是坐标原点,这时点集S中所有各 点相对轴OX有一个倾角。所有各点按倾角 递增排序后,如果某一点不是壳上顶点,则 它必然在两个壳顶点与点O形成的三角形内 部。 Graham扫描的实质是围绕已经按"倾 角"排序的各顶点进行一次扫描,在扫描过 程中消去在凸壳内部的点,留下以希望次序 排列的壳顶点
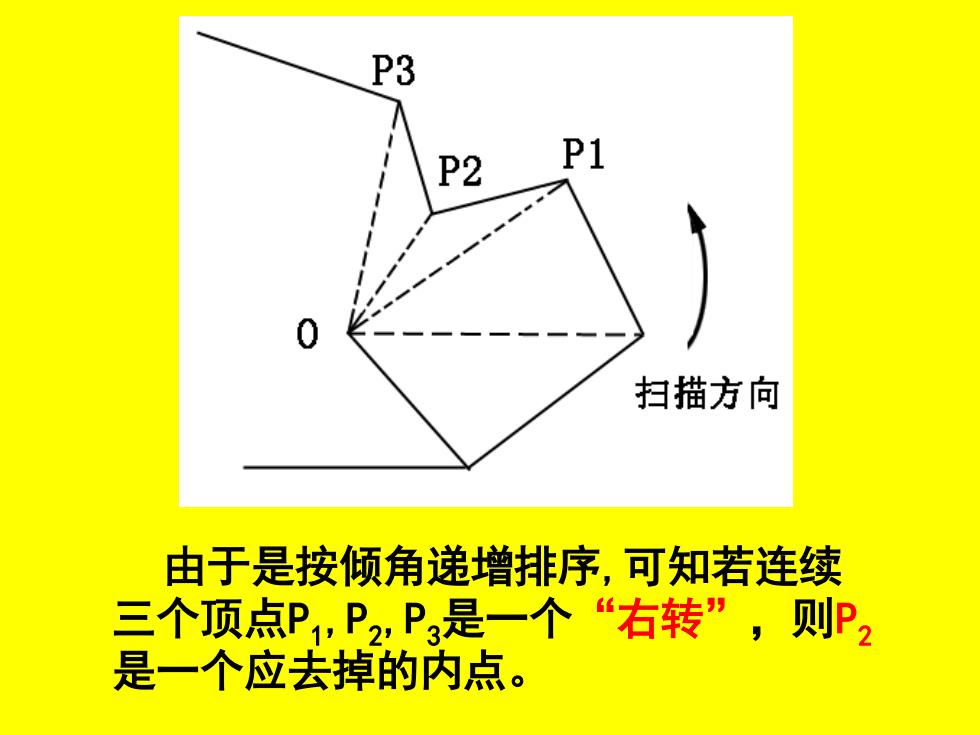
P3 P1 扫描方向 由于是按倾角递增排序,可知若连续 三个顶点P1,P2,P是一个“右转”,则P2 是一个应去掉的内点
由于是按倾角递增排序,可知若连续 三个顶点P1 ,P2 ,P3是一个“右转”,则P2 是一个应去掉的内点

对给出的三点P1,P2,P3,设它们的 坐标是(x1,y),(x2,y2),(x3,y),这时要 判断三点在P,处形成一个右转还是左转, 可以计算下面的行列式 X1 y1 △= X2 2 X3 寸3 其中△给出的是带有正负号的三角形PP,P3面 积的2倍,因此若△>0,则P1,P2,P3是左转;△<0, 则是右转;△=0,则三点共线
对给出的三点P1 ,P2 , P3 ,设它们的 坐标是(x1 ,y1 ),(x2 ,y2 ),(x3 ,y3 ),这时要 判断三点在P2处形成一个右转还是左转, 可以计算下面的行列式 1 3 y 3 x 1 2 y 2 x 1 1 y 1 x Δ= 其中△给出的是带有正负号的三角形P1 P2 P3面 积的2倍,因此若△>0,则P1 ,P2 ,P3是左转; △ <0, 则是右转; △ =0,则三点共线

实现此算法可选点集$中x坐标最小 的点为内点0,设想过0有一条向右的射线, 对其余各点,相对该射线计算倾角然后再 排序。 Graham扫描算法 1.〔倾角排序)选出输入点集$中x坐标最小的 点,若这样的点不唯一则再由其中选出y坐标最 小的点,设为0。设想有一条从0向右的射线0X, 对点集中其余每一点P,计算倾角P0X,再按倾角 排序,得点序列Q=0,Q2,Q3,Qn; 2.〔准备扫描)v←Q1;
实现此算法可选点集S中x坐标最小 的点为内点O,设想过O有一条向右的射线, 对其余各点,相对该射线计算倾角然后再 排序。 Graham扫描算法 1.〔倾角排序〕选出输入点集S中x坐标最小的 点,若这样的点不唯一则再由其中选出y坐标最 小的点,设为O。设想有一条从O向右的射线OX, 对点集中其余每一点P,计算倾角POX,再按倾角 排序,得点序列Q1 =O,Q2 ,Q3…,Qn ; 2.〔准备扫描〕v←Q1 ;