
第三节Coonsl曲面 P(u,w)=(x(u,w),r(u,w),z(u,w)) 0≤u≤1,0≤w≤1 OP(u,w) uw P(u,w) 0W= u Ou 02P(u,w).. 00=P(0,0). W Buow
第三节 Coons曲面 0 1,0 1 P( , ) ( ( , ), ( , ), ( , )) = u w u w x u w y u w z u w 0 0 P(0,0) P( , ) 2 P( , ) P( , ) = = = = u w u w uw uw u u w u uw u w uw
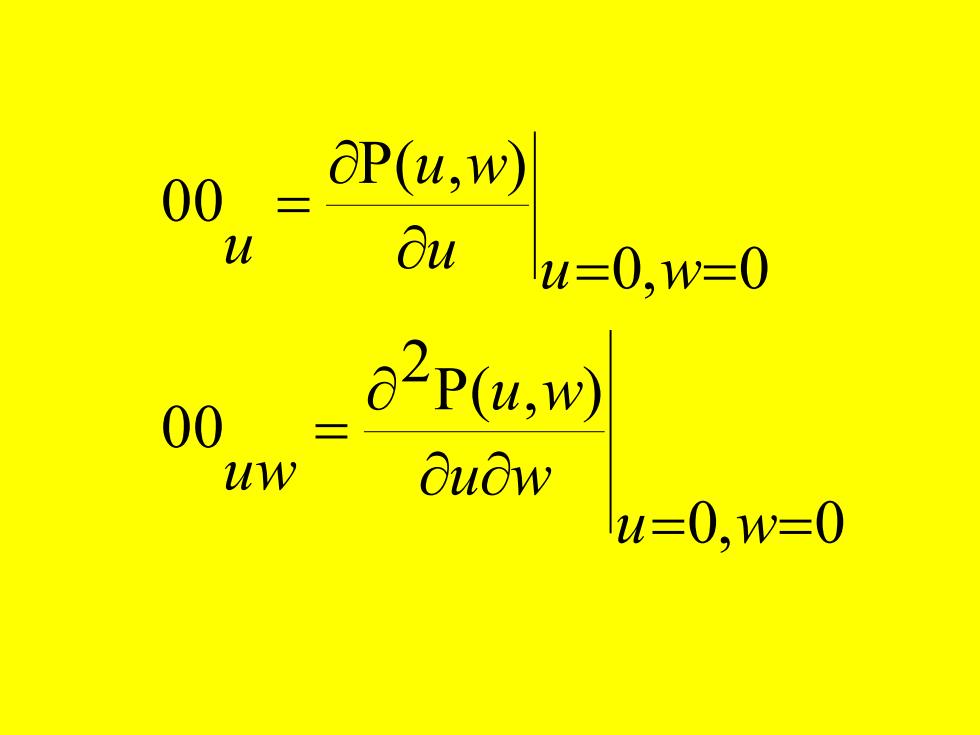
00 OP(u,w) u ∂u u=0,w=0 00 62P(u,w) uw ∂uaw u=0,w=0
0, 0 P( , ) 2 0 0 0, 0 P( , ) 0 0 = = = = = = u w u w u w uw u u w u w u

uw表示了曲面片的方程 0m,1M,0,1表示四条边界曲线 0,表示在边界线0上的点沿u向的一阶 偏导数向量,称边界线的切向量 0表示边界线0上的点沿向的一阶偏 导数向量,称边界线的跨界切向量。 u 1地au分别表示曲面片uw关于 和的二阶偏导数向量,于是0m表示 边界线0上的二阶切向量,0mw表示边 界线0上的二阶跨界切向量
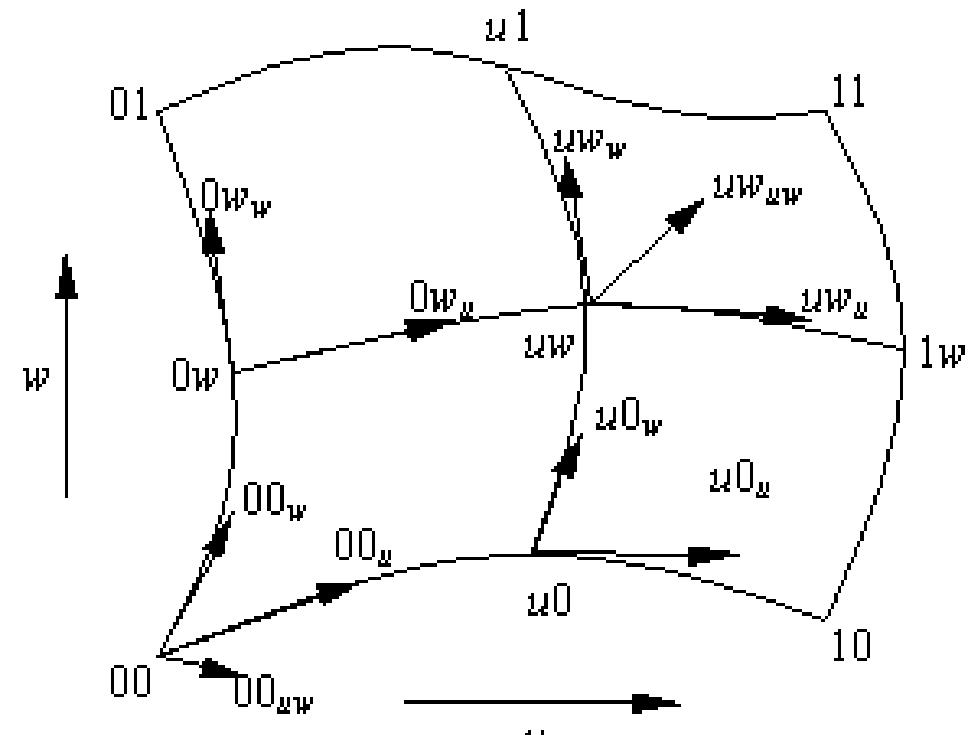
uw表示了曲面片的方程 0w,1w,u0,u1表示四条边界曲线 u0u表示在边界线u0上的点沿u向的一阶 偏导数向量,称边界线的切向量 u0w表示边界线u0上的点沿w向的一阶偏 导数向量,称边界线的跨界切向量。 uwuu ,uwuw,uwww分别表示曲面片uw关于 u和w的二阶偏导数向量,于是u0uu表示 边界线u0上的二阶切向量,u0ww表示边 界线u0上的二阶跨界切向量

umm为曲面片P在点(u,の处的扭 曲向量。特别,用00,01,10,11 分别表示曲面片四个角点时,00 01g10:11就分别表示在四 角点的扭曲向量
uwuw为曲面片P在点(u,w)处的扭 曲向量。特别,用00,01,10,11 分别表示曲面片四个角点时,00uw, 01uw,10uw,11uw就分别表示在四个 角点的扭曲向量
1u1 11 11HΨ1W LW Ow 11w 1 10w 00u 1μ0 10 00

构造具有指定边界曲线的曲面片 Coons?给出的一个解法是:寻找 两个混合函数f()和f(),它们 是连续的,并且满足f(0)=1 f6(1)=0,.f(0)=0,f(1)=1 ,且 f6(t)+f(t)=1,0≤t≤1。 利用这样的混合函数,通过四条 边界构造曲面片,并通过叠加修正 曲面片,产生满足用户需要的曲面
构造具有指定边界曲线的曲面片 Coons给出的一个解法是:寻找 两个混合函数f0 (t)和f1 (t),它们 是连续的 , 并 且 满 足 f0 (0)=1 , f0 (1)=0 , f1 (0)=0 , f1 (1)=1 , 且 f0 (t)+f1 (t)=1,0≤t≤1。 利用这样的混合函数,通过四条 边界构造曲面片,并通过叠加修正 曲面片,产生满足用户需要的曲面

若给定四条边界曲线0,1,0W, 1W且0≤≤1,0≤≤1 在向进行线性插值,得到直纹面为: P,w)=0w.0w+f(0)-1w 其中/(ω+才(0=1,0≤u≤1
若给定四条边界曲线u0,u1,0w, 1w,且0≤u≤1,0≤w≤1 在u向进行线性插值,得到直纹面为: ( ) 1,0 1 1 ( ) 0 ( ) 1 1 ( ) 0 0 ( , ) 1 P + = = + f u f u u u w f u w f u w 其中

在M向进行线性插值,得到 直纹面为 P(uw)=o(w)u0+(w)ul 其中f0(w)+f()=1,0≤w≤1 若把这两张直纹面叠加可得 到一张新曲面P。(w,W:
在w向进行线性插值,得到 直纹面为: ( ) 1,0 1 1 ( ) 0 ( ) 1 1 ( ) 0 0 ( , ) 2 P + = = + f w f w w u w f w u f w u 其中 若把这两张直纹面叠加可得 到一张新曲面Ps (u,w):

P.(u,w)=P(u,w)+P,(u,w) =f(u).0w+f(u)·lw +f(w)·u0+f(w)ul 其中f,(w)+f,(u)=1,0≤w≤1 其中f(w)+f(w)=1,0≤w≤1 P。(山,励上的任意一点,其位移矢量包含两 个部分,一部分是由于线性插值而产生的位 移,另一部分是由于边界曲线而产生的位移
( ) ( ) 1,0 1 ( ) ( ) 1,0 1 ( ) 0 ( ) 1 ( ) 0 ( ) 1 P ( , ) P ( , ) P ( , ) 0 1 0 1 0 1 0 1 1 2 + = + = + + = + = + f w f w w f u f u u f w u f w u f u w f u w s u w u w u w 其中 其中 Ps (u,w)上的任意一点,其位移矢量包含两 个部分,一部分是由于线性插值而产生的位 移,另一部分是由于边界曲线而产生的位移

为消除P(山,の中由于线性插值而产生 的位移,需要构造一个新的曲面P3(u,吻 P3a,w=0w[U00)-00+fw)-10 +fw[f0.01+/w)11叮 =f0(w)fo()-00+f0(w)f()10 +(w)u)01+(w)(u)-11 其中f(0+f(0=1,0≤u≤1, w+fw=1,0≤w≤1
( ) 1,0 1 1 ( ) 0 ( ) 1,0 1 1 ( ) 0 ( ) 1 1 1 ( ) 1 ( ) 0 1 0 ( ) 1 ( ) 1 0 1 ( ) 0 ( ) 0 0 0 ( ) 0 ( ) 1 1] 1 ( ) 0 1 0 ( )[ 1 ( ) 1 0] 1 ( ) 0 0 0 ( )[ 0 ( , ) 3 P + = + = + + = + + + = + f w f w w f u f u u f w f u f w f u f w f u f w f u f w f u f u u w f w f u f u 其中 , 为消除Ps (u,w)中由于线性插值而产生 的位移,需要构造一个新的曲面P3 (u,w)