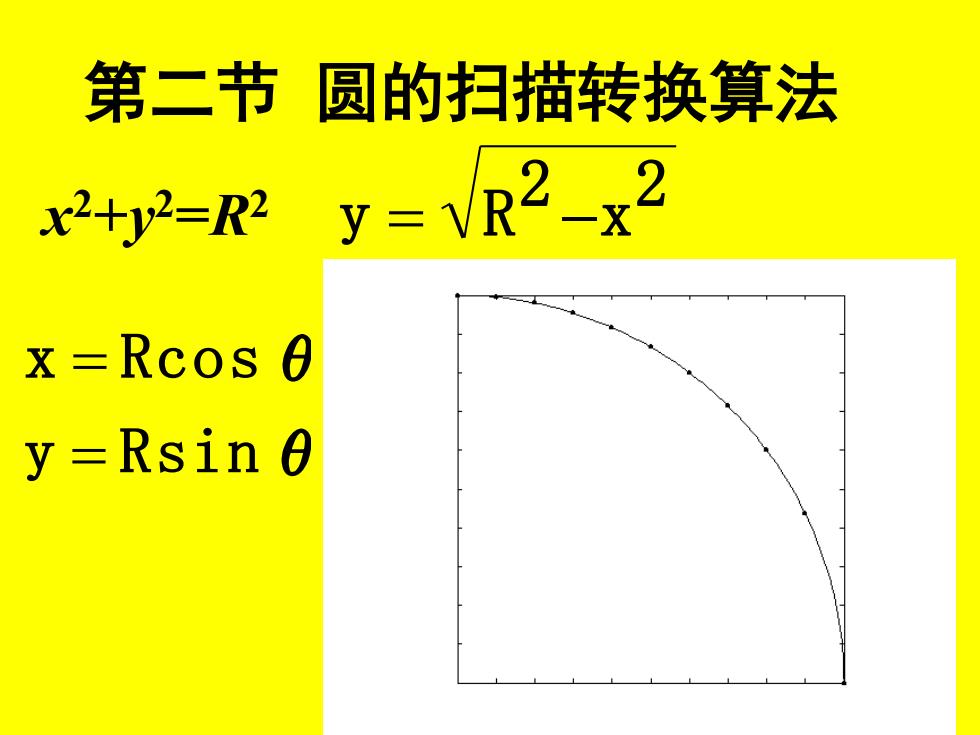
第二节圆的扫描转换算法 2+2-R2y=VR2-x2 x=Rcos 0 y=Rsin 0
第二节 圆的扫描转换算法 x 2+y 2=R2 2 x 2 y = R − y Rsinθ x Rcosθ = =

(x,y) (x,y) (y,x) (y.x) 了45 (y,) (y-x) (x,y) (,y)

Bresenhami画圆算法 在0≤X≤y的18圆周上,象素坐 标x值单调增加,y值单调减少。 设第步已确定(xy)是要画 圆上的象素点,看第+1步象素点 (X+1y+1)应如何确定。下一个象 素点只能是(+-)或者(+))中 的一个
Bresenham画圆算法 在0≤x≤y的1/8圆周上,象素坐 标x值单调增加,y值单调减少。 设第i步已确定(xi ,yi)是要画 圆上的象素点,看第i+1步象素点 (xi+1,yi+1)应如何确定。下一个象 素点只能是 或者 中 的一个 ( 1, ) i i ( +1, −1) x + y i i x y

dH=(x1+1)2+y子-R2 dD=R2-(x1+1)2-(y1-1)2
2 1 ) i ( y 2 1 ) i ( x 2 R D d 2 R 2 i y 2 1 ) i ( x H d = − + − − = + + −

D:=d-d 精确圆弧是③,则d4>0和d>0.若p,0,d。≤0,必有p>0。 得出结论:p做判别量,p,<O选H点为下 一个象素点,当p,≥0时,选D点为下一个象 素点
pi = dH −dD 精确圆弧是③,则dH >0和dD >0.若pi 0,必有pi 0,dD≤0,必有pi >0。 得出结论: pi做判别量, pi <0选H点为下 一个象素点,当pi≥0时,选D点为下一个象 素点

从P;计算+打 P:=2(¥+1)2+2y2-2y-2R2+1 P+1乃:=201- -i+1+》+4x;+6 当p,≥0时,应选D点,即选y+1=yi一 P+1=p+4(x,-y:)+10
从 p i 计算 i+1 p 1 2 2 2 2 2 2 = 2( +1) + − − R + i y i y i x i p ) 4 6 1 2 2 1 2( 1 + + + + − − + − = + i x i y i y i y i y i p i p 当pi≥0时,应选D点,即选 1 1 = − + i y i y pi+1 = pi + 4(xi − yi ) +10

当p,<O时,应选H,即选 i+1=yi P+1=P:+4x,+6 画圆的起始点是(0,B, 即0,y=R,代入前式,令=1, 就得到: 6=3-55
当pi <0时,应选H,即选 i y i y = +1 pi+1 = pi + 4xi + 6 画圆的起始点是(0,R), 即x1 =0,y1 =R,代入前式,令i=1, 就得到: R i p =3−2

void BresenhamCircle(int R) int x,y,p; x=0;y=R; p=3-2*R; for(;x=0) & p+=4*(X-y)+10; y-9 }
void BresenhamCircle(int R) { int x,y,p; x=0; y=R; p=3-2*R; for(;x=0) { p+=4*(x-y)+10; y--; }

else {p+=4*x+6 只需修改语句SetPixel(x,y),画 八个对称的点,就可以画出全部圆周 。若加一个平移,就可以画出圆心在 任意位置的圆周
else { p+=4*x+6; } } } 只需修改语句SetPixel(x,y),画 八个对称的点,就可以画出全部圆周 。若加一个平移,就可以画出圆心在 任意位置的圆周

第三节 区域填充算法 区域是指光栅网格上的一组象素。 区域填充是把某确定的象素值送入 到区域内部的所有象素中。 区域填充方法分为两大类。 区域由多边形围成,区域由多边形 的顶点序列来定义;另一类方法是通 过象素的值来定义区域的内部,相应 的技术称为是以象素为基础的
第三节 区域填充算法 区域是指光栅网格上的一组象素。 区域填充是把某确定的象素值送入 到区域内部的所有象素中。 区域填充方法分为两大类。 区域由多边形围成,区域由多边形 的顶点序列来定义;另一类方法是通 过象素的值来定义区域的内部,相应 的技术称为是以象素为基础的