
第一章 1.2直线的投影
第一章 1.2直线的投影
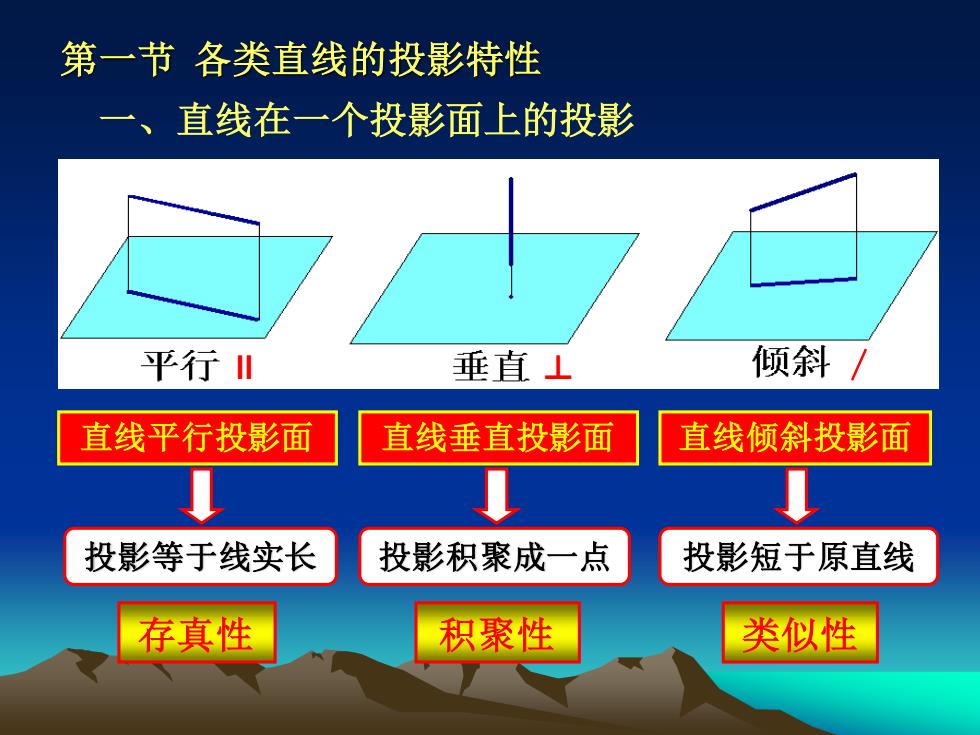
第一节各类直线的投影特性 直线在一个投影面上的投影 平行川 垂直⊥ 倾斜 直线平行投影面 直线垂直投影面 直线倾斜投影面 投影等于线实长 投影积聚成一点 投影短于原直线 存真性 积聚性 类似性
第一节 各类直线的投影特性 一、直线在一个投影面上的投影 直线平行投影面 积聚性 直线垂直投影面 存真性 直线倾斜投影面 类似性 投影等于线实长 投影积聚成一点 投影短于原直线 ∥ ⊥ /
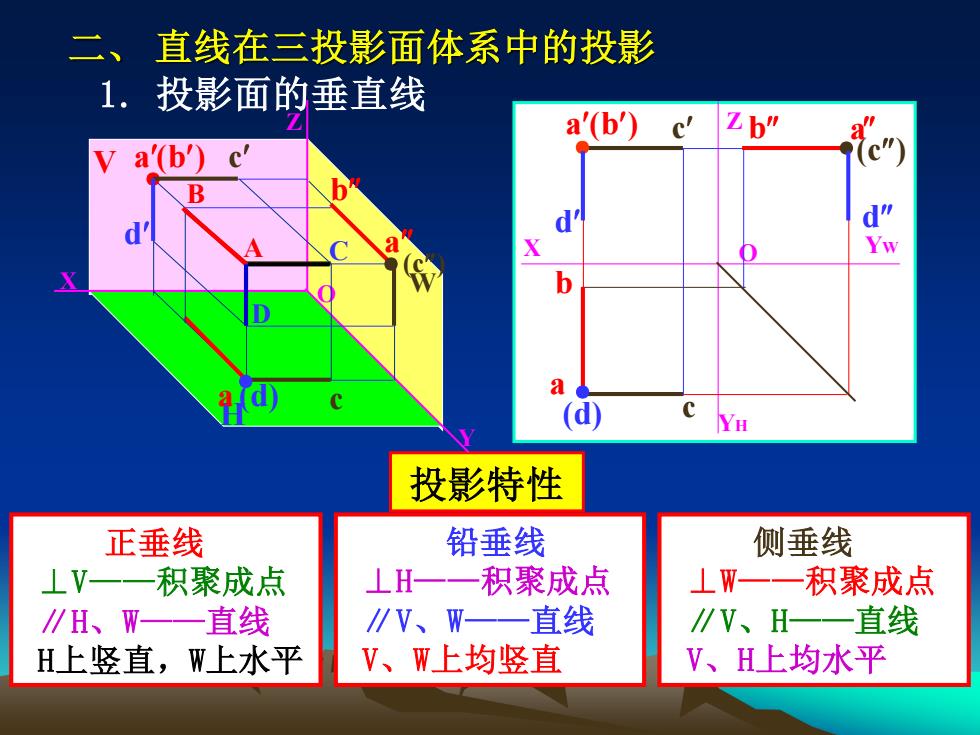
二、直线在三投影面体系中的投影 1.投影面的垂直线 a'(b')c Z b" a(b') c B d" Yw b 投影特性 正垂线 铅垂线 侧垂线 ⊥V- 积聚成点 ⊥H一一积聚成点 ⊥W一一积聚成点 ∥H、W一一直线 ∥V、W—一直线 ∥V、H一一直线 H上竖直,W上水平 V、W上均竖直 V、H上均水平
二、 直线在三投影面体系中的投影 1. 投影面的垂直线 正垂线 ⊥V——积聚成点 ∥H、W——直线 H上竖直,W上水平 投影特性 铅垂线 ⊥H——积聚成点 ∥V、W——直线 V、W上均竖直 侧垂线 ⊥W——积聚成点 ∥V、H——直线 V、H上均水平 X Y Z O V H W A a a (b) B C (c) a (d) ● ● ● D c c d b Z X YH O YW a (b) b a b (c) (d) c c ● ● a ● d d
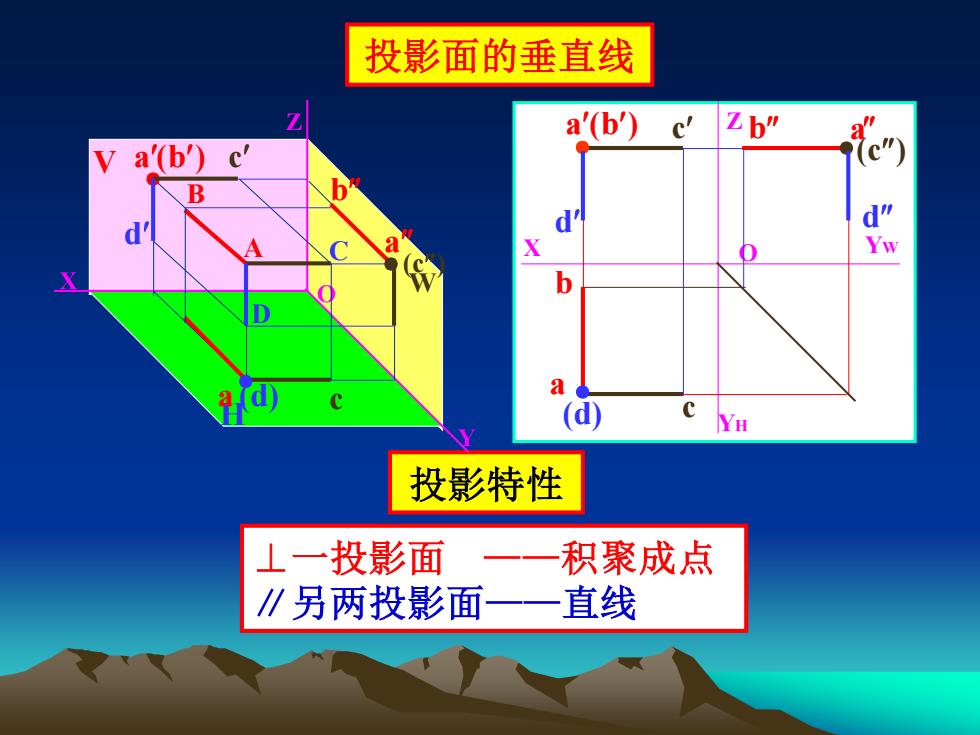
投影面的垂直线 a'(b) c Z b" a(b') B d" Yw b (d) YH 投影特性 ⊥一投影面 积聚成点 ∥另两投影面 直线
投影面的垂直线 ⊥一投影面 ——积聚成点 ∥另两投影面——直线 投影特性 X Y Z O V H W A a a (b) B C (c) a (d) ● ● ● D c c d b Z X YH O YW a (b) b a b (c) (d) c c ● ● a ● d d
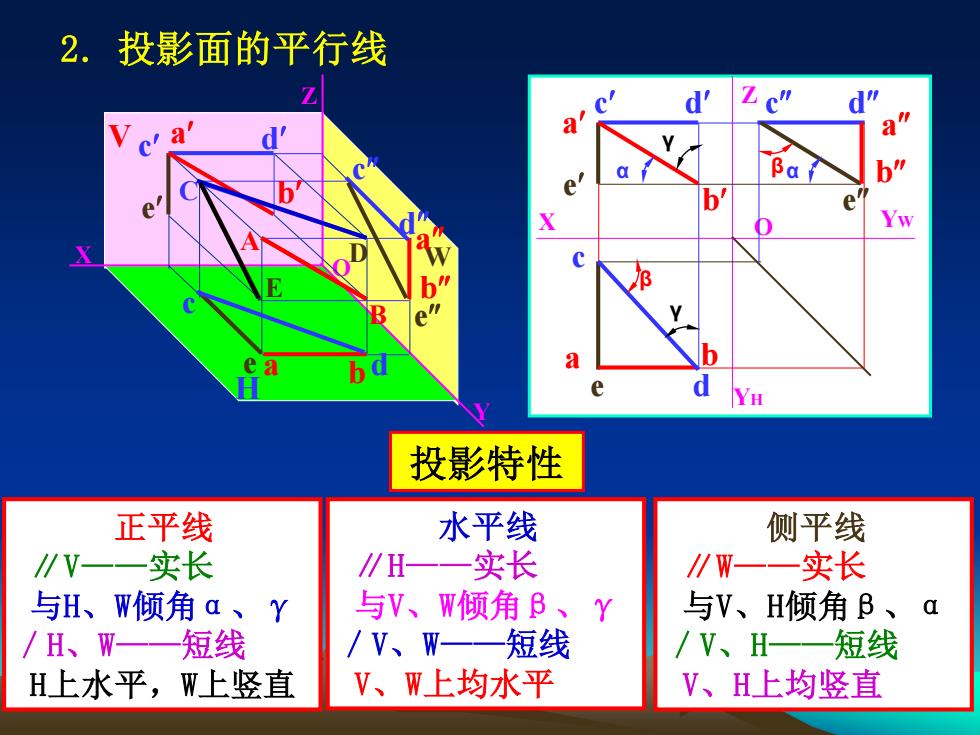
2.投影面的平行线 d' d a Yw a e YH 投影特性 正平线 水平线 侧平线 ∥V- 一实长 ∥H一一实长 ∥W一一实长 与H、W倾角a、Y 与V、W倾角B、Y 与V、H倾角B、 a /H、W一 短线 /V、W一一短线 /V、H一一短线 H上水平,W上竖直 V、W上均水平 V、H上均竖直
2. 投影面的平行线 投影特性 正平线 ∥V——实长 与H、W倾角α、γ /H、W——短线 H上水平,W上竖直 水平线 ∥H——实长 与V、W倾角β、γ /V、W——短线 V、W上均水平 侧平线 ∥W——实长 与V、H倾角β、α /V、H——短线 V、H上均竖直 X Y Z O V H W A a a a B C d c e D d b e c Z X YH O YW a b c c a e b d d a c e d b e E c d b b e β γ β γ α α
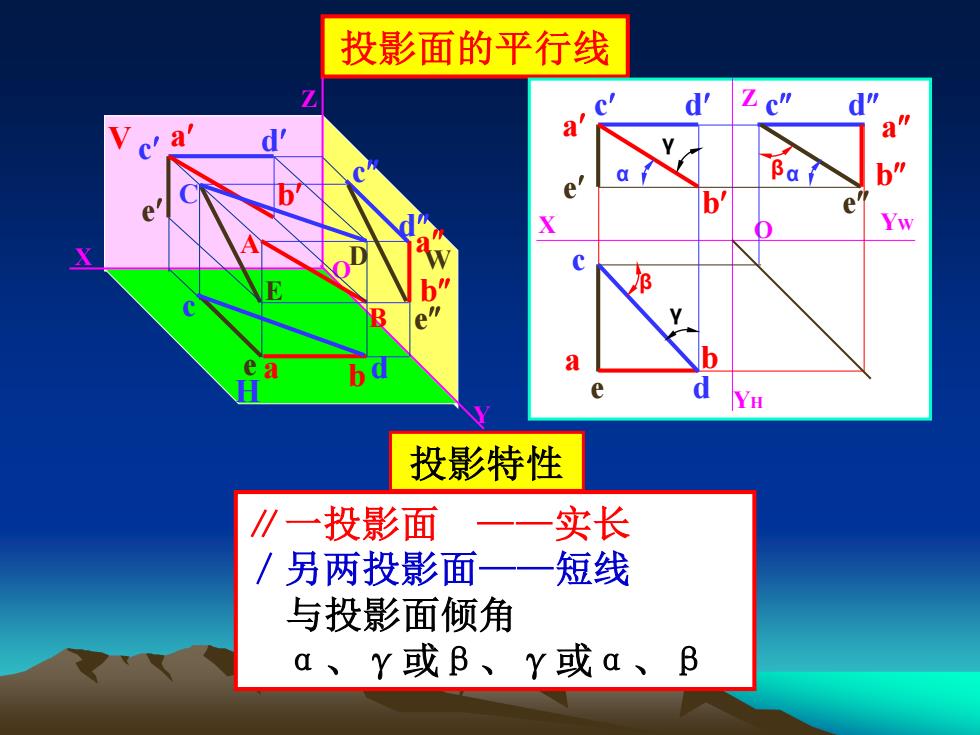
投影面的平行线 d' c a b" D Yw ba a e YH 投影特性 ∥一投影面 一一实长 /另两投影面 一一 短线 与投影面倾角 a、Y或B、Y或a、B
投影面的平行线 投影特性 ∥一投影面 ——实长 /另两投影面——短线 与投影面倾角 α、γ或β、γ或α、β X Y Z O V H W A a a a B C d c e D d b e c Z X YH O YW a b c c a e b d d a c e d b e E c d b b e β γ β γ α α
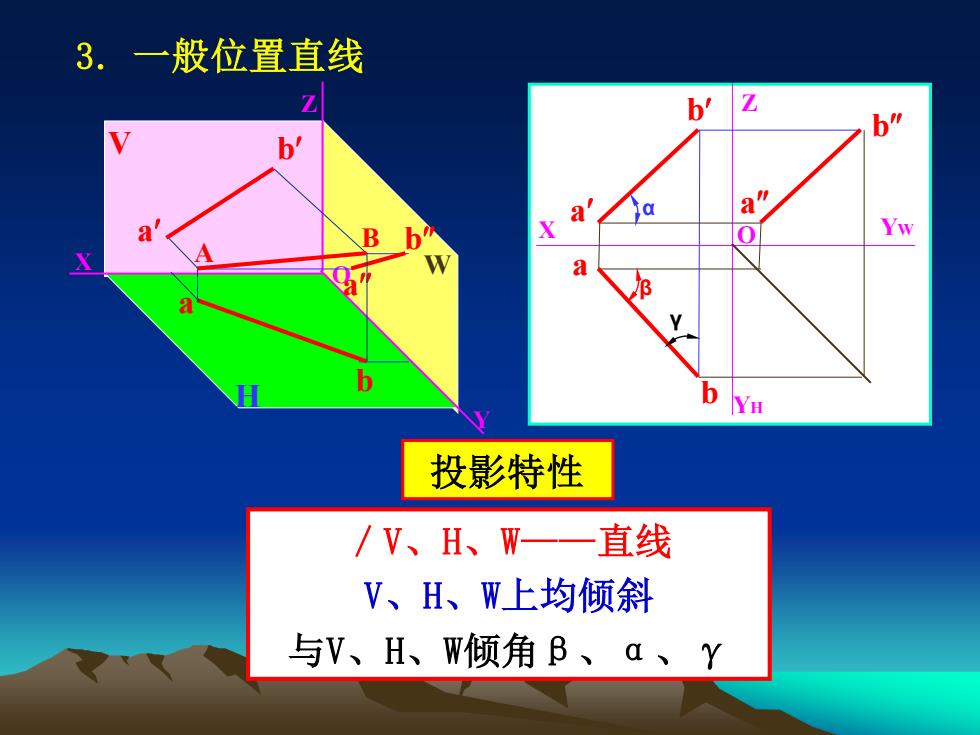
3.一般位置直线 b' Z b" b' B Yw a b YH 投影特性 /V、H、W一一直线 V、H、W上均倾斜 与V、H、W倾角B、a、Y
3. 一般位置直线 投影特性 /V、H、W——直线 V、H、W上均倾斜 与V、H、W倾角β、α、γ X Y Z O V H W a a a B A b b b Z X YH O YW a b a b a b β γ α
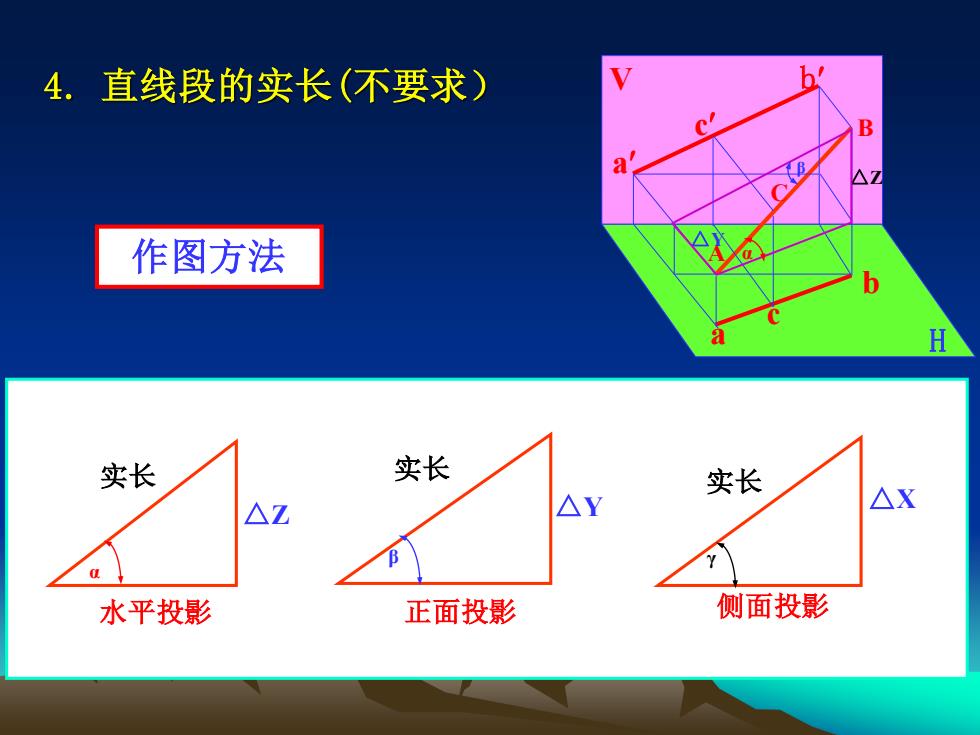
4.直线段的实长(不要求) B 作图方法 H 实长 实长 实长 △Z △Y △X 水平投影 正面投影 侧面投影
A B C V H b c c b a a △Z △Y α β α 实长 △Z 水平投影 实长 γ △X 侧面投影 实长 β △Y 正面投影 4. 直线段的实长(不要求) 作图方法

例1已知AB的实长及其一个投影,求作其另一投影。 a b' ◆过b'以为半径画弧 ◆过a'作a'b'垂线 0 交圆弧于a得△y ◆过a、b'分别作 水平线和垂线 y ◆量取△y 求点b ◆连接a、b
例1 已知AB的实长及其一个投影,求作其另一投影。 b a1 ◆过b以l为半径画弧 a a b X O l l Δy Δy ● ● ◆过a作a b垂线 交圆弧于a1得Δy ◆过a、b分别作 水平线和垂线 ◆量取Δy 求点b ◆连接a、b

第二节直线上的点 投影特性 B 从属性 若点在直线上 其投影必在直线的同面投影上 且符合点的投影规律 若一投影不在直线同名投影上一一点必不在直线上 定比性(定比定理) 点所分割的两线段长度之比=其投影长度之比 AC ac a'c' a CB cb c'b' c"b
第二节 直线上的点 ◆ 从属性 投影特性 若点在直线上 其投影必在直线的同面投影上 且符合点的投影规律 ◆ 定比性(定比定理) 点所分割的两线段长度之比 = 其投影长度之比 c b a c c b a c cb ac CB AC = = = A B C V H b c c b a a ● ● ● 若一投影不在直线同名投影上——点必不在直线上