北京化工大学：《现代工程图学》课程教学资源（PPT课件）第一章 1.1 点的投影

第一章 1.1点的投影

第一章 1.1点的投影

第一节点的投影 、点在一个投影面上的投影 空间点A、投影面P 过空间点A的投射线 与投影面P产生的交点 点A在P面上的投影a 个投影面上的投影 B:B2 不能确定点的空间位置 采用多面投影

A P P b 空间点 A 、投影面 P B1 B2 ● B3 ● ● 一个投影面上的投影 第一节 点的投影 ●a 过空间点A 的投射线 与投影面 P 产生的交点 ——点 A 在 P 面上的投影 a′ 采用多面投影 一、点在一个投影面上的投影 不能确定点的空间位置 ● ●

二、点在两个投影面上的投影 投影面 ◆ 正立投影面 正面或V面 ◆水平投影面一一 水平面或H面 投影轴 0X轴 一一V、H面的交线 两投影面互相垂直

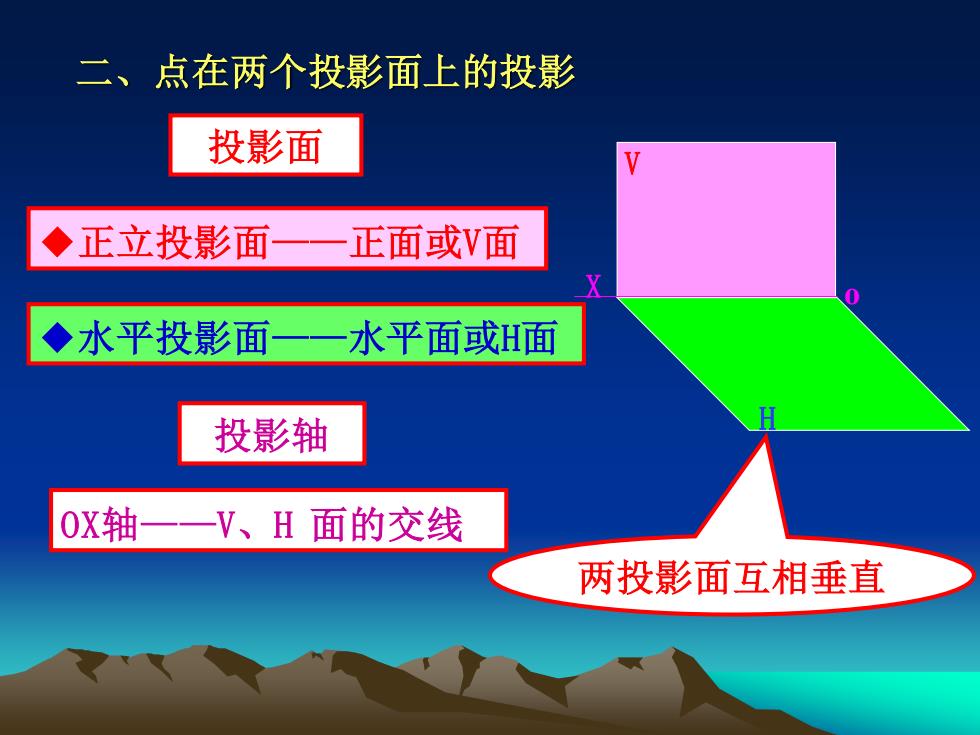
投影面 ◆正立投影面——正面或V面 ◆水平投影面——水平面或H面 H V X o 投影轴 OX轴——V、H 面的交线 两投影面互相垂直 二、点在两个投影面上的投影

点A在两个投影面上的投影 空间点A 过点A的射线 与两投影面的交点 a. a' 点A的正面投影 a一一点A的水平投影 H 过a、a'作0X垂线 交0X于ax 空间点一—大写字母 投影 一小写字母

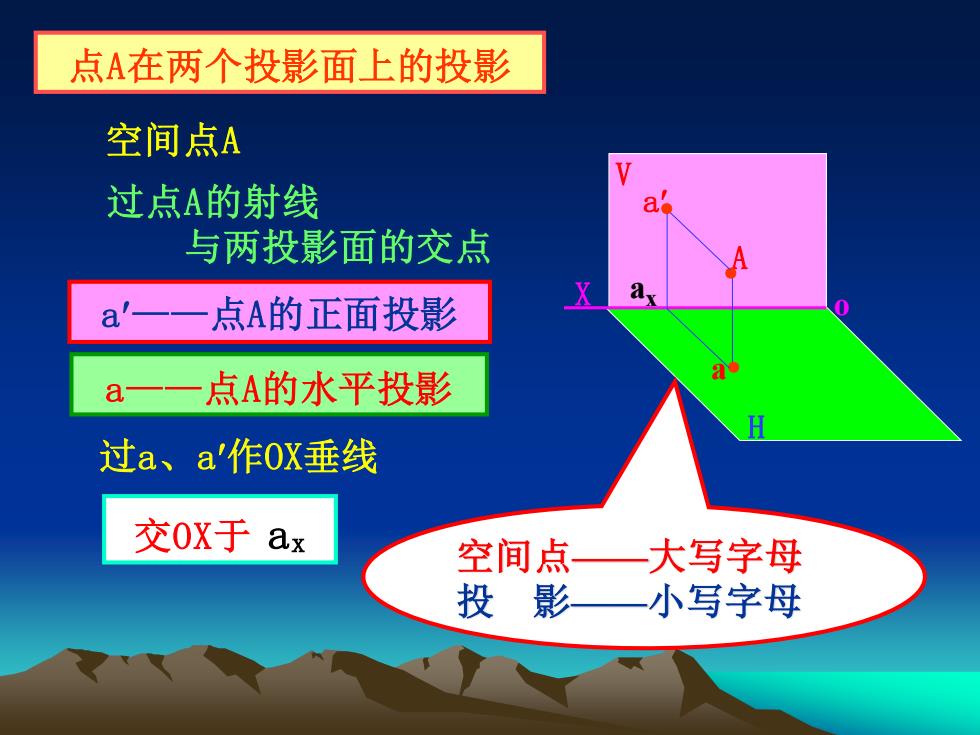
H V o X 点A在两个投影面上的投影 a——点A的正面投影 a——点A的水平投影 空间点——大写字母 投 影——小写字母 a● A● 空间点A 过点A的射线 与两投影面的交点 ax a ● 过a、a作OX垂线 交OX于 ax

投影面展开 不动 ax 0 ax H 向下翻

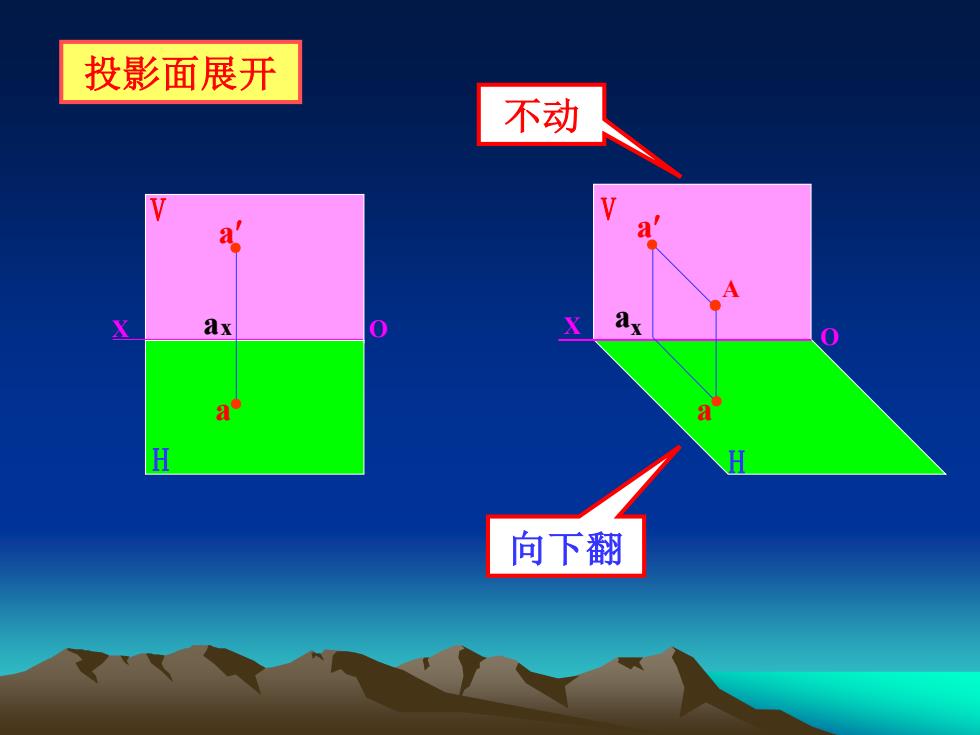
V H 投影面展开 X O X V H a a ax A ● ● O ● a ● a x ● a 向下翻 不动

X a 投影规律 ★a'a⊥0X轴 ★ aax Aa'=A到V面的距离 a'ax= Aa=A到H面的距离

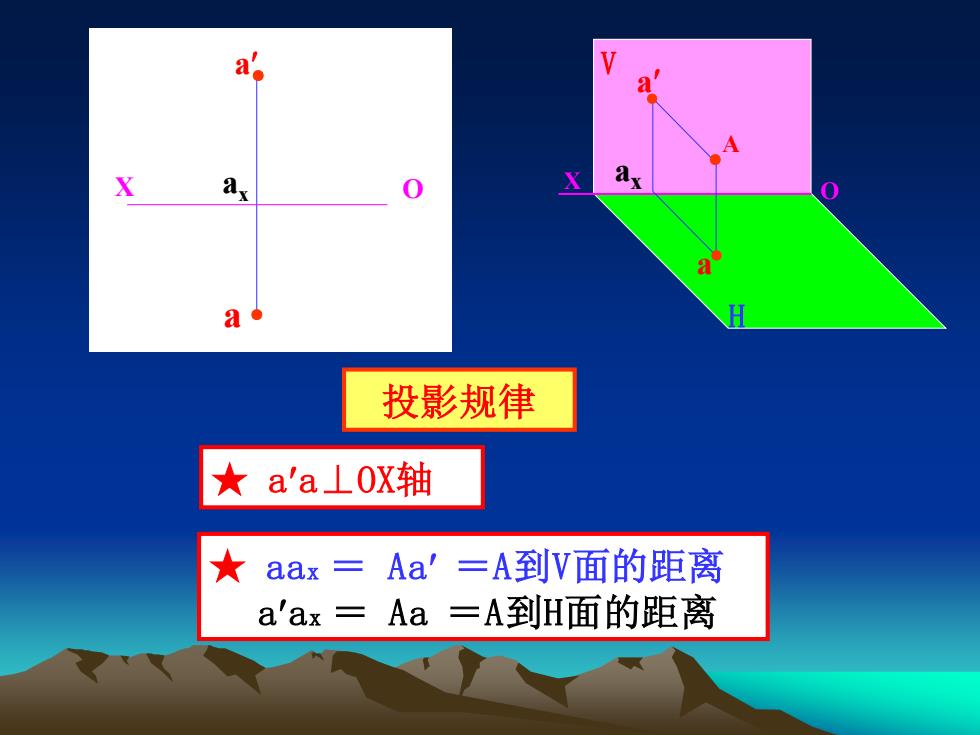
投影规律 ★ aa⊥OX轴 ★ aax ＝ Aa ＝A到V面的距离 aax ＝ Aa ＝A到H面的距离 ● X O a ax a ● X V H a a ax A ● ● O ●

三、投影面体系的建立 确定点的空间位置 三投影面体系 投影面 V一正立投影面（正面或V面） H一水平投影面（水平面或H面） W 侧立投影面（侧面或W面） 投影轴 OX轴一V、H面的交线 0Y轴一H、W面的交线 0Z轴一V、W面的交线 三投影面互相垂直

三、 投影面体系的建立 确定点的空间位置 三投影面体系 投影面 V V—正立投影面（正面或V面） H H—水平投影面（水平面或H面） W W—侧立投影面（侧面或W面） 三投影面互相垂直 投影轴 o X OX轴—V、H 面的交线 Y OY轴—H、W 面的交线 Z OZ轴—V、W 面的交线

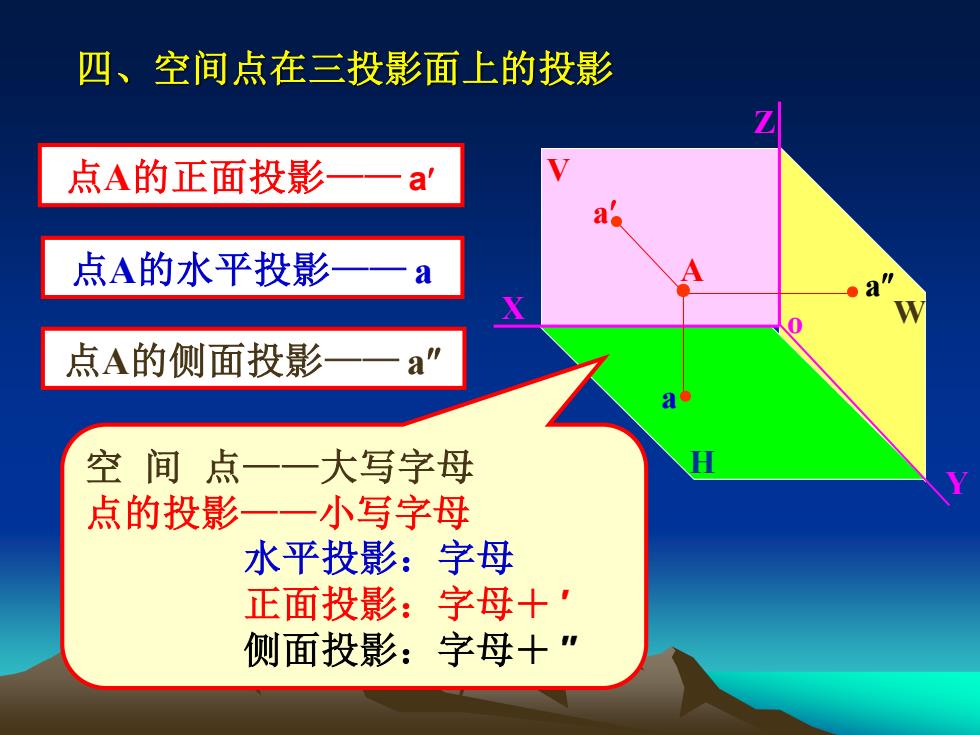
四、空间点在三投影面上的投影 点A的正面投影 a 点A的水平投影 a 点A的侧面投影 空间点一一大写字母 点的投影 小写字母 水平投影：字母 正面投影：字母十' 侧面投影：字母十

W H V o X Z Y 四、空间点在三投影面上的投影 点A的正面投影—— a 点A的水平投影—— a 点A的侧面投影—— a ● a a● a ● A ● 空 间 点——大写字母 点的投影——小写字母 水平投影：字母 正面投影：字母＋ ′ 侧面投影：字母＋ ″

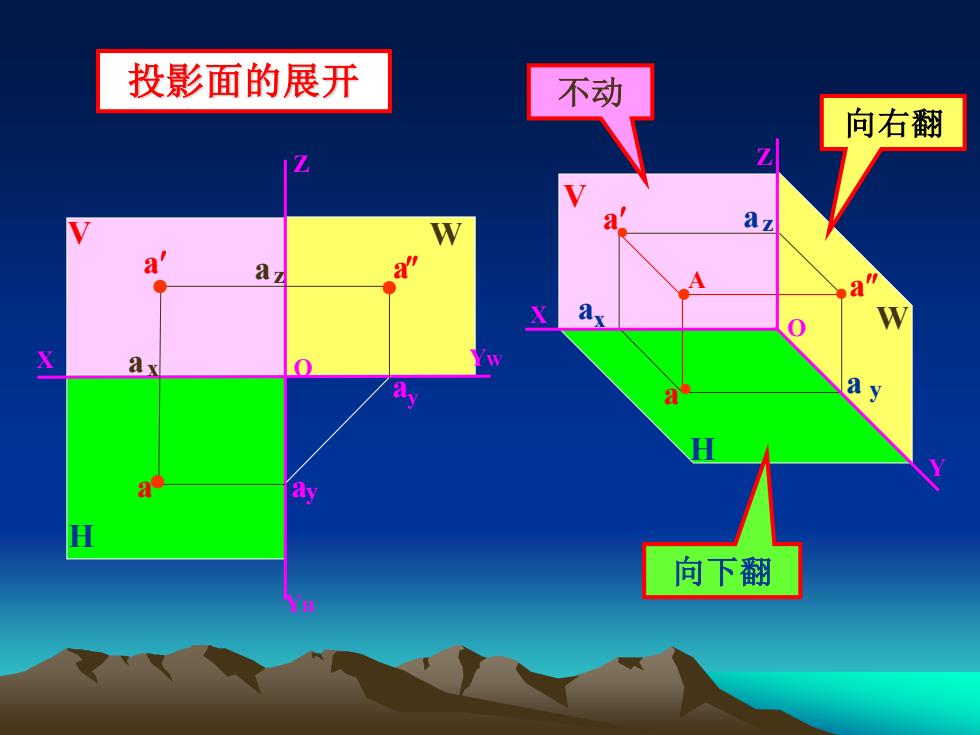
投影面的展开 不动 向右翻 az a a 向下翻

投影面的展开 V W H ● ● ● ● X Y Z O V H W A a a  a  a x a z a y 向右翻 向下翻 不动 a a Z aa  y a y a X Y H Y W O  ●● z a● x

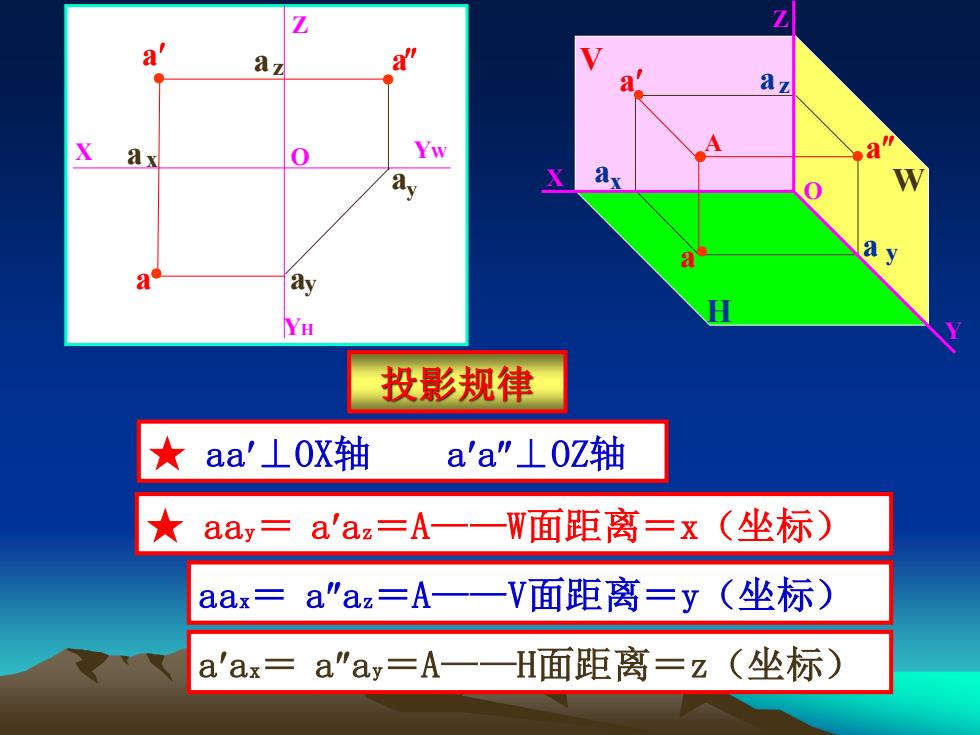
Z az a" az X ax Yw 》y a y YH 投影规律 ★ aa'⊥0X轴 a'a"⊥0z轴 ★ aay=a'az=A 一一W面距离=x（坐标) aax=a"az=A一一V面距离=y（坐标) a'ax-a"ay=A- 一一H面距离=z(坐标)

● ● ● ● X Y Z O V H W A a a a ax az a y a a Z a a y a y a X YH O YW  ● ● z a ● x 投影规律 ★ aa⊥OX轴 aa⊥OZ轴 ★ aay＝ aaz＝A——W面距离＝x（坐标） aax＝ aaz＝A——V面距离＝y（坐标） aax＝ aay＝A——H面距离＝z（坐标）