北京化工大学：《现代工程图学》课程教学资源（PPT课件）第一章 1.4 直线与平面的相对位置

第一章 1.4直线与平面 的相对位置

第一章 1.4直线与平面 的相对位置

第一节平行问题 平行 直线与平面 平面与平面 →、 直线与平面平行 定理 直线平行平面上的某一直线 则必平行该平面

第一节 平行问题 平行 一、直线与平面平行 直线与平面 平面与平面 定 理 直线平行平面上的某一直线 则必平行该平面

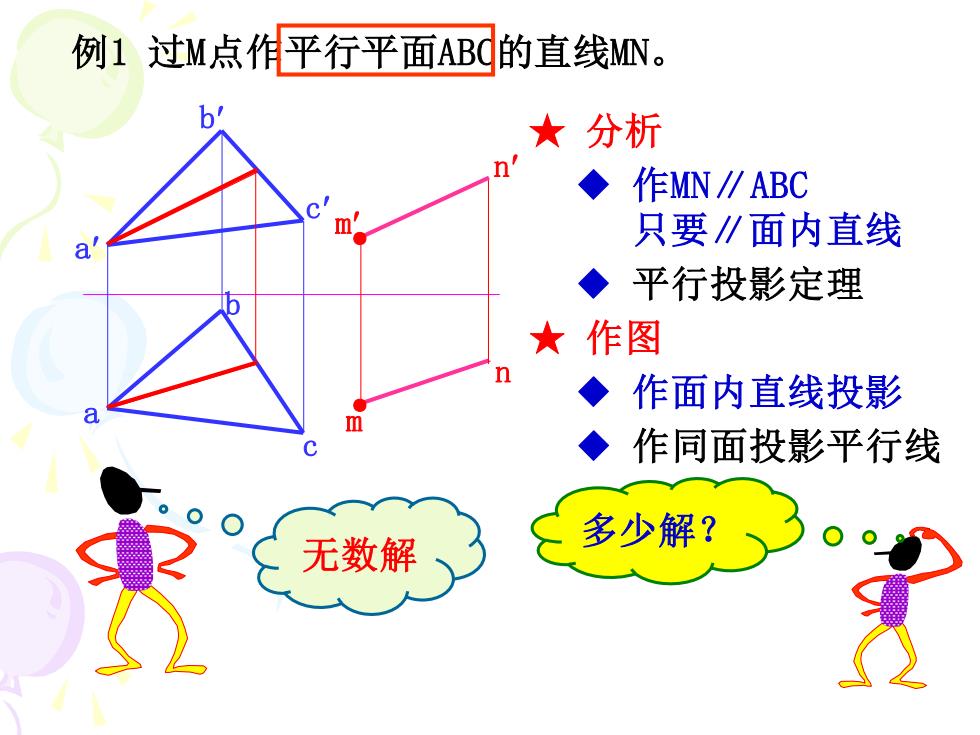
例1过M点作平行平面ABd的直线MN。 b ★分析 ◆作MN∥ABC m 只要∥面内直线 a ◆平行投影定理 ★作图 ◆ 作面内直线投影 a ◆作同面投影平行线 多少解？ 无数解

例1 过M点作平行平面ABC的直线MN。 ★ 分析 ◆ 作MN∥ABC 只要∥面内直线 n ● ● a c b m a b c m n ◆ 平行投影定理 ★ 作图 ◆ 作面内直线投影 ◆ 作同面投影平行线 无数解 多少解？

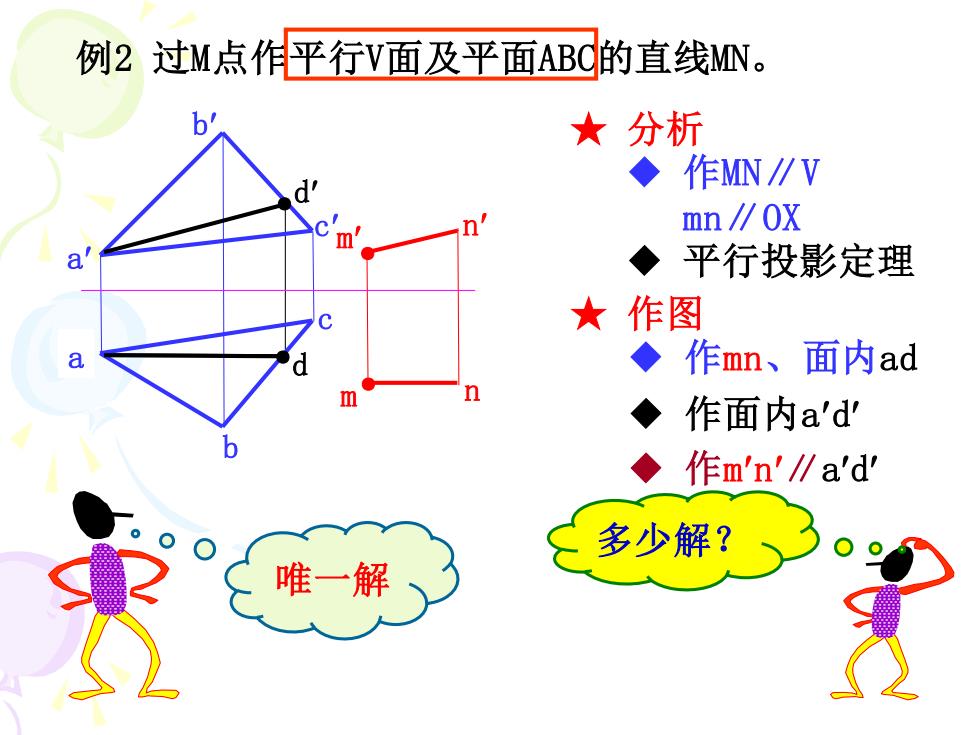
例2过M点作平行V面及平面ABd的直线MN。 b ★分析 ◆作MN∥V n mn∥0X ◆平行投影定理 ★作图 a ◆作mn、i 面内ad m n ◆ 作面内a'd' ◆ 作m'n'∥a'd 多少解？ 唯一解

例2 过M点作平行V面及平面ABC的直线MN。 ★ 分析 ◆ 作MN∥V mn∥OX ◆ 平行投影定理 ★ 作图 ◆ 作mn、面内ad ◆ 作面内ad 唯一解 多少解？ n c n ● ● b a m a b c m ◆ 作mn∥ad ● d ●d

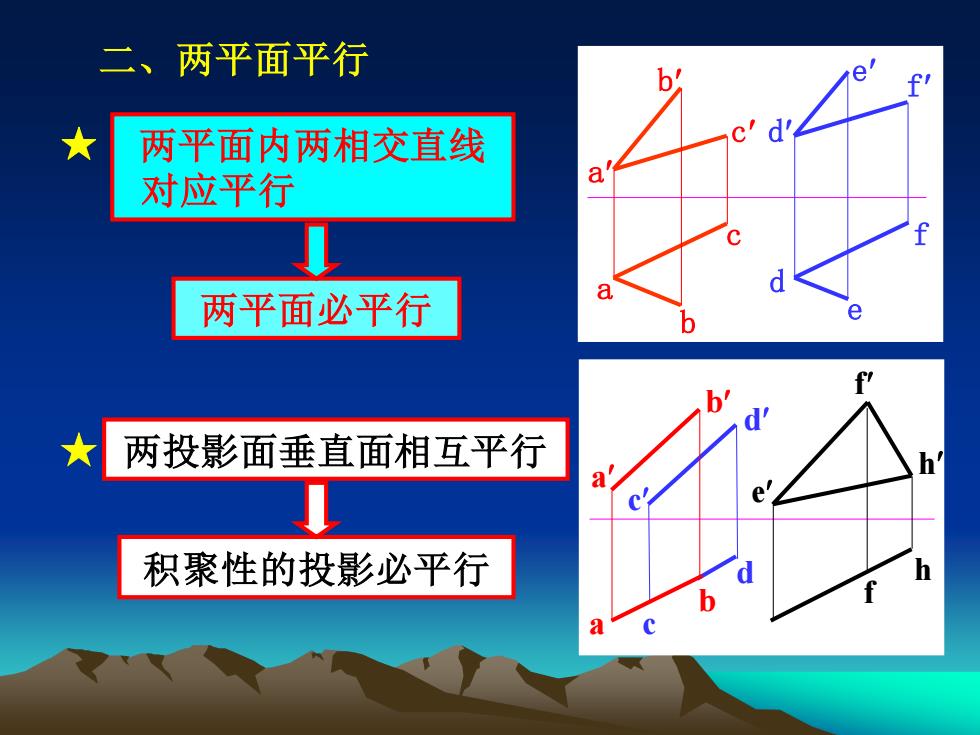
二、两平面平行 b ★ 两平面内两相交直线 对应平行 a 两平面必平行 8 d fr b' 两投影面垂直面相互平行 h 积聚性的投影必平行 b f

二、两平面平行 c b f  d e a a b c d e f h a b c d e f h a b c d e f ★ 两平面内两相交直线 对应平行 ★ 两投影面垂直面相互平行 两平面必平行 积聚性的投影必平行

例3平面ABC与DEF相互平行，完成平面DEF的投影。习题集 P30,26 2 b d 0 2 a ★过d作线∥12一 求e ★过a'作a'1'∥e'f'一一作al 女过e作线∥al 一 求f ★过1'作1'2'∥de'一一作12 ★连接de、ef

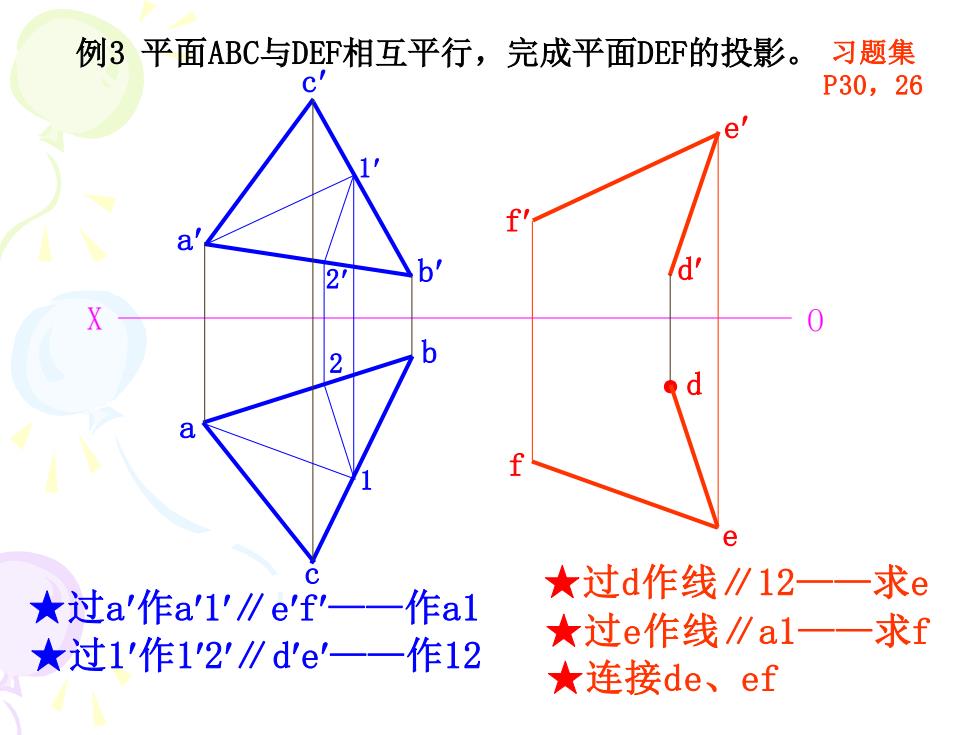
例3 平面ABC与DEF相互平行，完成平面DEF的投影。 X O a ● d b b c f a e d c e f 2 1 2 1 ★过a作a1∥ef——作a1 ★过1作12∥de——作12 ★过d作线∥12——求e ★过e作线∥a1——求f ★连接de、ef 习题集 P30，26

例4已知平面P（AB∥CD)平行三角形EFG, 习题集 试完成平面P的投影。 P30,25 ◆过e'作c'd'平行线 交f'g于1' 6 ◆求作1，连接1e ◆连接cb' 过e'作c'b平行线 g 交f'g于2 0 ◆求作2，连接2e g ◆过a作1e平行线 2 过b'作垂线求b b ◆过b作2e平行线 过c'作垂线求c d ◆过c作ab平行线 过d'作垂线求d ◆加粗ab、cd

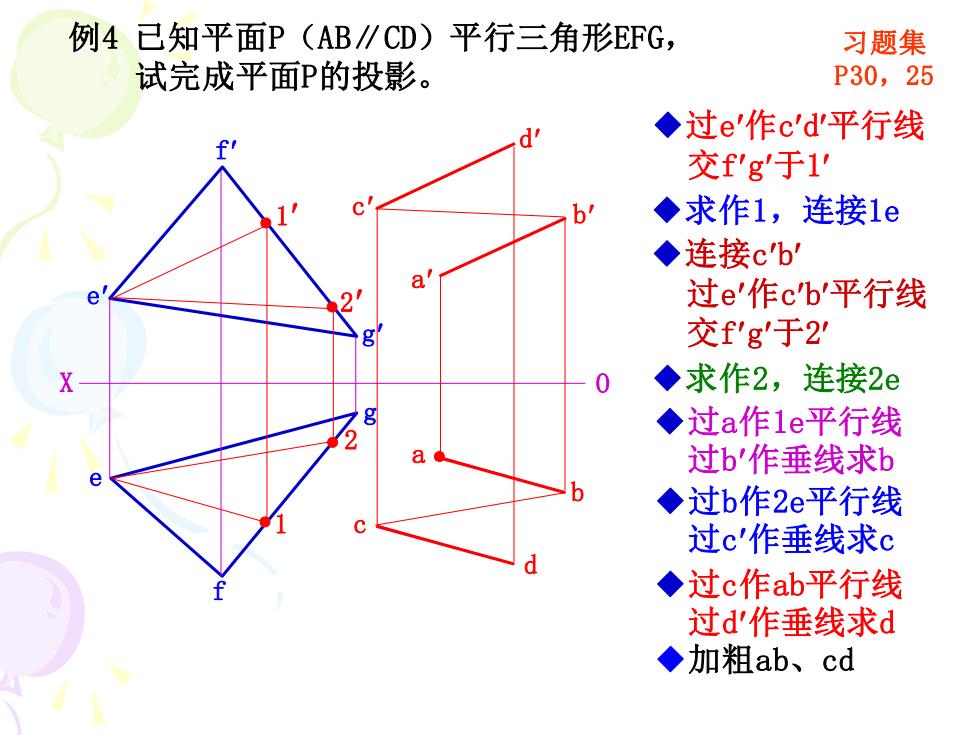
f e e b ● X O g g f d a c a 例4 已知平面P（AB∥CD）平行三角形EFG， 试完成平面P的投影。 习题集 P30，25 ● ● ◆过e作cd平行线 交fg于1 ◆过a作1e平行线 过b作垂线求b ◆加粗ab、cd b d c ● ● 1 2 1 2 ◆求作1，连接1e ◆连接cb 过e作cb平行线 交fg于2 ◆求作2，连接2e ◆过b作2e平行线 过c作垂线求c ◆过c作ab平行线 过d作垂线求d

第二节相交问题 相交 直线与平面 平面与平面 直线与平面相交 交点一一直线与平面的共有点 ★求直线与平面的交点 重点 ★判断可见性

第二节 相交问题 相交 直线与平面 平面与平面 一、直线与平面相交 交点——直线与平面的共有点 重点 ★ 求直线与平面的交点 ★ 判断可见性

1.至少其一处特殊位置 例5求直线MN与平面ABC的交点K,并判断可见性。 ★分析 b ◆abc一一直线 ABC⊥H面 铅垂面 ◆mn与之交点一一k 1'(2 ★求交点 ◆作k' ◆判断可见性 k'n'可见 m 2 kn在前 ★判断可见性 b k 根据重影点判断 a 1k(面)在前 2k(线)在后 2k'不可见

例5 求直线MN与平面ABC的交点K，并判断可见性。 ★ 分析 ◆ abc——直线 ABC⊥H面——铅垂面 ◆ mn与之交点——k ★ 求交点 ◆ 作k ◆ 判断可见性 kn在前——kn可见 b b a m c n c n a m k 1(2) k ● 2 ● 1 ● ● ★ 判断可见性 ——根据重影点判断 1k（面）在前 2k（线）在后 2k不可见 ● 1. 至少其一处特殊位置

例6求直线MN与平面ABC的交点K,并判断可见性。 ★分析 m ◆m(n) 点 MN⊥H面 铅垂线 ◆k也在此点 ★求交点 a 1'(2） n ◆作k ★判断可见性 ◆取点I、 Ⅱ的1'、2 m(n)2 I在面，在前 一一可见 C Ⅱ在线，在后 一一不可见 a k2不可见 另一判断方法K以下一一 面在前，可见 K以上一一 线在前，可见

例6 求直线MN与平面ABC的交点K，并判断可见性。 ★ 分析 ◆ m(n)——点 MN⊥H面——铅垂线 ◆ k也在此点 ★ 求交点 ◆ 作k ★ 判断可见性 ◆ 取点Ⅰ、Ⅱ的1 、2 Ⅰ在面，在前——可见 Ⅱ在线，在后——不可见 k b m(n)● m n c b a a c 1(2) k ● ●2 1 ● ● k2不可见 K以下——面在前，可见 K以上——线在前，可见 另一判断方法