
第二章 曲面立体的截切
第二章 曲面立体的截切
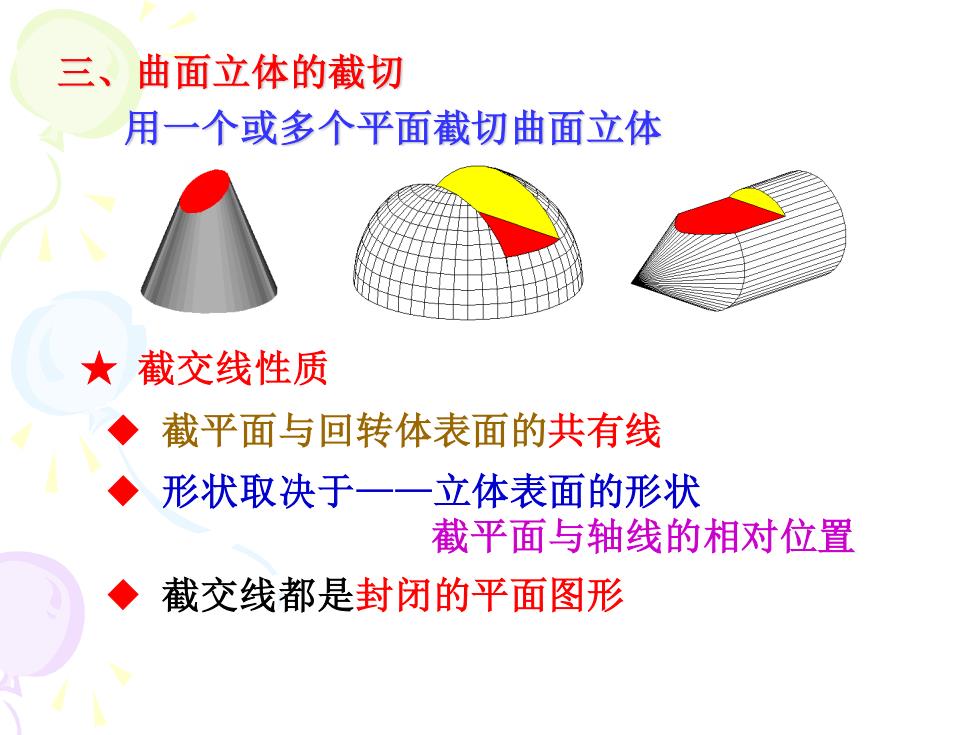
三、曲面立体的截切 用一个或多个平面截切曲面立体 ★截交线性质 截平面与回转体表面的共有线 形状取决于一一 立体表面的形状 截平面与轴线的相对位置 截交线都是封闭的平面图形
三、曲面立体的截切 ◆ 截平面与回转体表面的共有线 ◆ 形状取决于——立体表面的形状 截平面与轴线的相对位置 ◆ 截交线都是封闭的平面图形 ★ 截交线性质 用一个或多个平面截切曲面立体
大求截交线的步骤 确定截交线形状 分析回转体的形状 截平面与回转体轴线的相对位置 分析截平面与投影面的相对位置 明确截交线的投影特性 画出截交线的投影 找出截交线已知投影 回求作线上点的投影 预见未知投影 ◎判断可见性 光滑连接各点 截交线的投影为非圆曲线时 △找特殊点 △补充中间点
◆ 分析回转体的形状 截平面与回转体轴线的相对位置 ◆ 分析截平面与投影面的相对位置 明确截交线的投影特性 ◆ 画出截交线的投影 ★ 求截交线的步骤 截交线的投影为非圆曲线时 △ 找特殊点 ◎ 光滑连接各点 ◎ 判断可见性 确定截交线形状 找出截交线已知投影 预见未知投影 △ 补充中间点 ◎ 求作线上点的投影
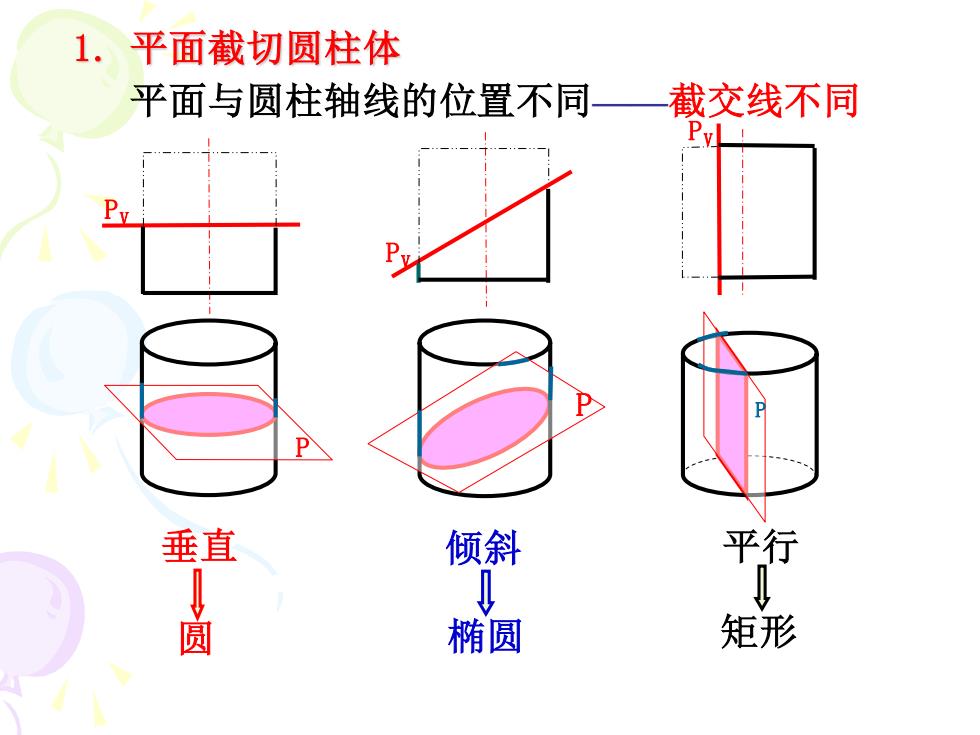
1.平面截切圆柱体 平面与圆柱轴线的位置不同 截交线不同 Pvl 垂直 倾斜 平行 圆 椭圆 矩形
1. 平面截切圆柱体 平面与圆柱轴线的位置不同——截交线不同 垂直 倾斜 平行 PV P PV P PV P 圆 椭圆 矩形
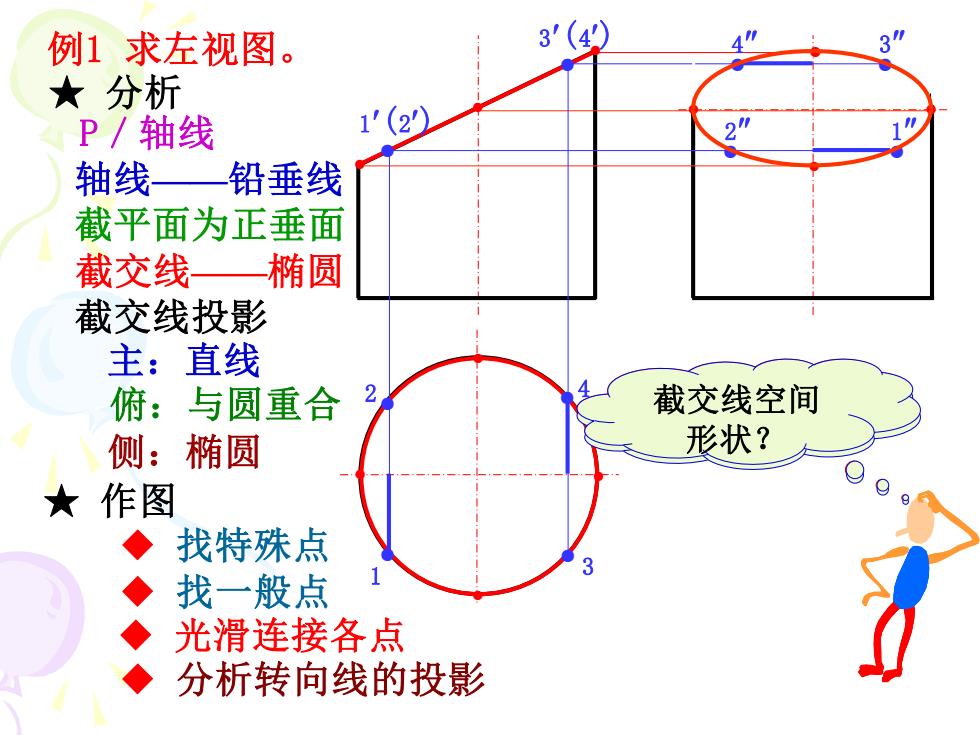
例1求左视图。 3'(4) ★分析 P/轴线 1'(2) 22 轴线 铅垂线 截平面为正垂面 截交线 —椭圆 截交线投影 主:直线 俯: 与圆重合 2 截交线空间 侧:椭圆 形状? ★ 作图 ◆ 找特殊点 2 ◆ 找一般点 ◆ 光滑连接各点 ◆ 分析转向线的投影
● ● ● 例1 求左视图。 ◆ 找特殊点 ◆ 光滑连接各点 ◆ 分析转向线的投影 P/轴线 轴线——铅垂线 截平面为正垂面 主:直线 俯:与圆重合 侧:椭圆 ★ 分析 ★ 作图 截交线投影 ● ● ● ● ● ● ● 截交线——椭圆 侧面形状? 已知投影? 截交线空间 形状? ◆ 找一般点 ● 2 ● 1(2) ● 1 2● ● 1 ● 3(4) ●4 ● 3 ● ● 3 ● 4
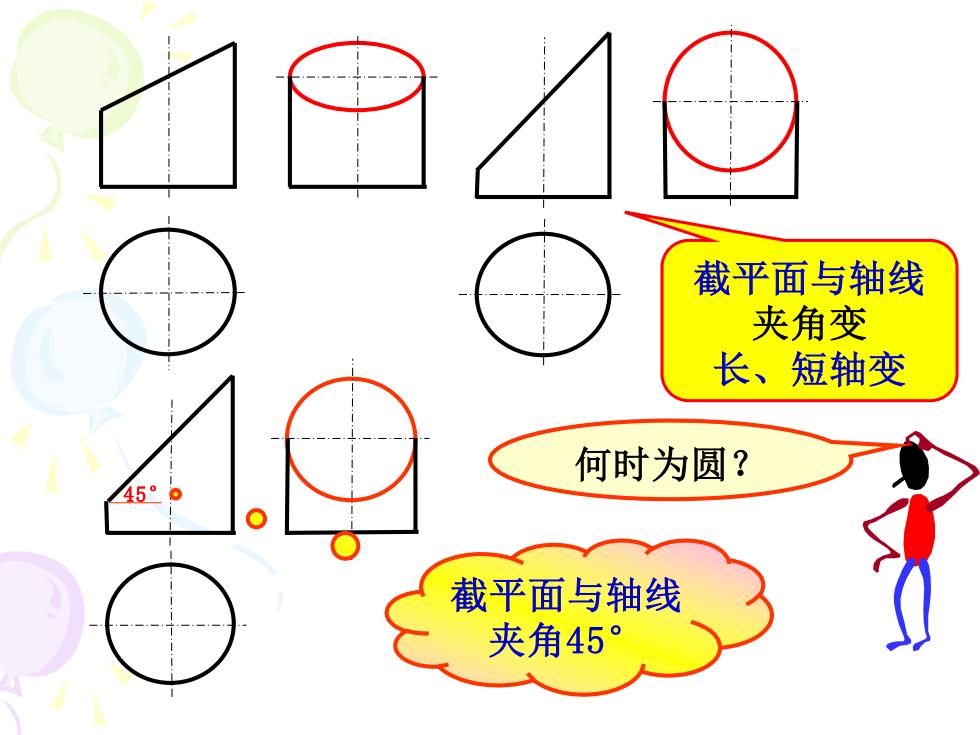
截平面与轴线 夹角变 长、短轴变 何时为圆? 截平面与轴线 夹角45°
截平面与轴线 夹角变 长、短轴变 45° 何时为圆? 截平面与轴线 夹角45°
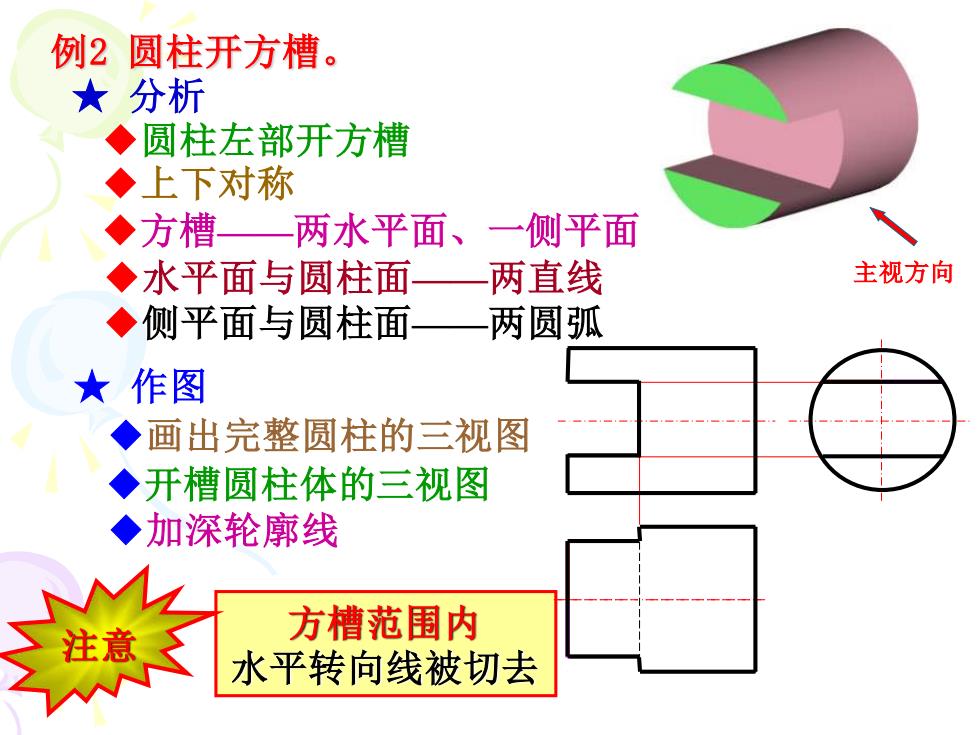
例2圆柱开方槽。 ★分析 ◆圆柱左部开方槽 ◆上下对称 ◆方槽 两水平面、一侧平面 ◆水平面与圆柱面 两直线 主视方向 ◆侧平面与圆柱面 两圆弧 ★作图 ◆画出完整圆柱的三视图 ◆开槽圆柱体的三视图 ◆加深轮廓线 注意 方槽范围内 水平转向线被切去
例2 圆柱开方槽。 ★ 分析 ◆圆柱左部开方槽 ◆上下对称 ◆方槽——两水平面、一侧平面 ◆水平面与圆柱面——两直线 ◆侧平面与圆柱面——两圆弧 ★ 作图 主视方向 ◆画出完整圆柱的三视图 ◆开槽圆柱体的三视图 方槽范围内 水平转向线被切去 ◆加深轮廓线 注意
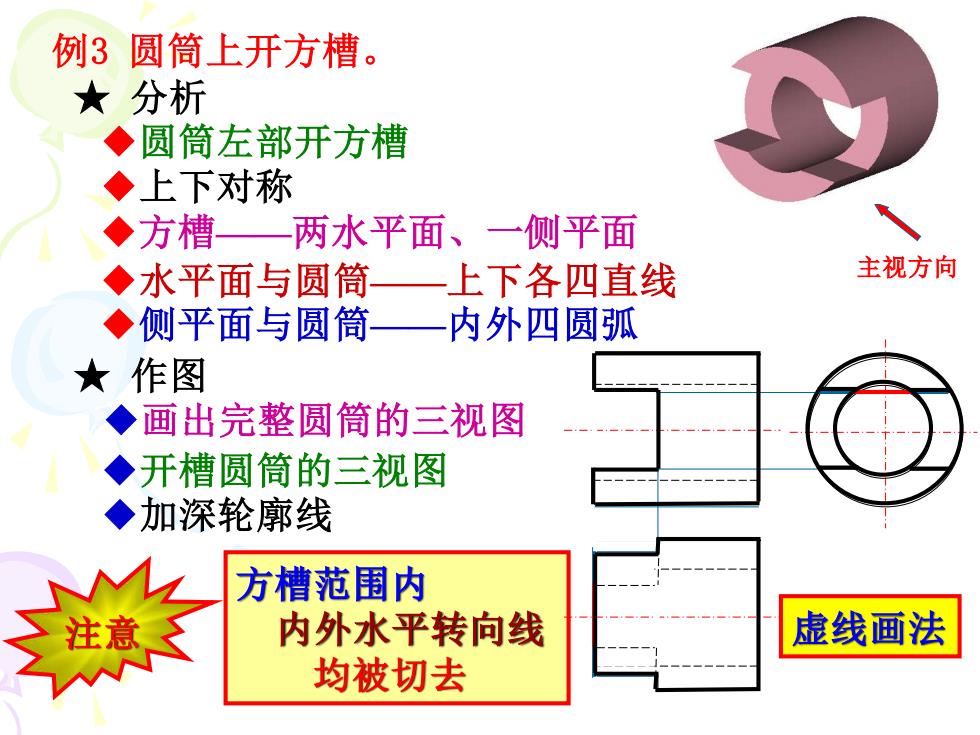
例3圆筒上开方槽。 女分析 ◆圆筒左部开方槽 ◆上下对称 ◆方槽— 两水平面、一侧平面 ◆水平面与圆筒一上下各四直线 主视方向 ◆侧平面与圆筒一内外四圆弧 ★作图 ◆画出完整圆筒的三视图 ◆开槽圆筒的三视图 ◆加深轮廓线 方槽范围内 内外水平转向线 虚线画法 均被切去
例3 圆筒上开方槽。 ★ 分析 ◆圆筒左部开方槽 ◆上下对称 ◆方槽——两水平面、一侧平面 ◆水平面与圆筒——上下各四直线 ◆侧平面与圆筒——内外四圆弧 ★ 作图 ◆画出完整圆筒的三视图 ◆开槽圆筒的三视图 ◆加深轮廓线 主视方向 虚线画法 方槽范围内 内外水平转向线 均被切去 注意
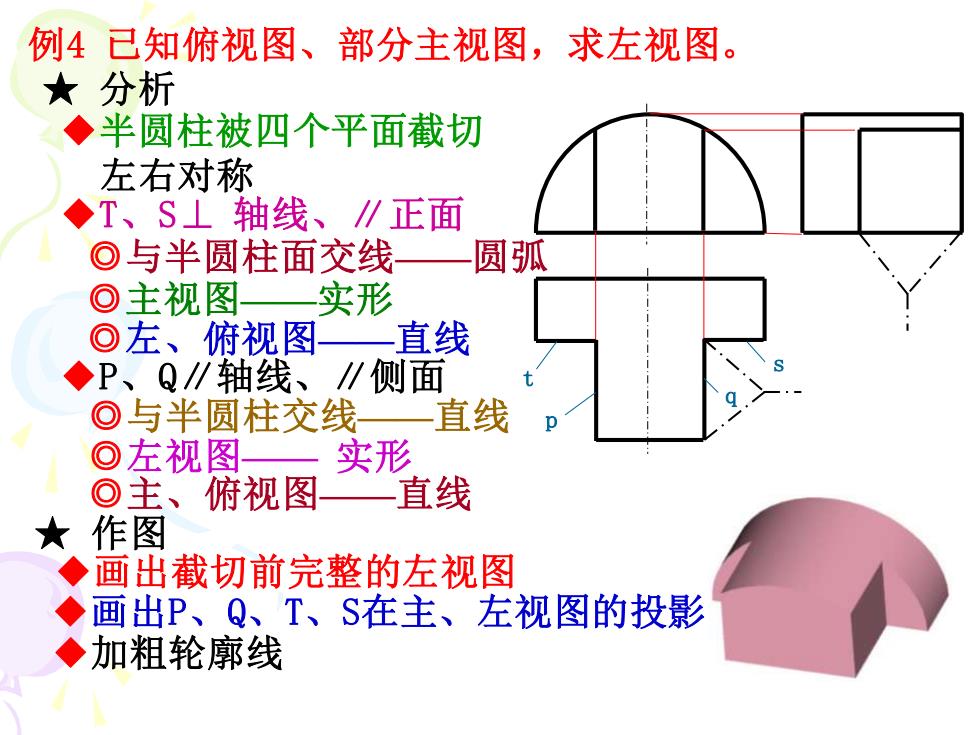
例4已知俯视图、部分主视图,求左视图。 ★分析 ◆ 半圆柱被四个平面截切 左右对称 ◆T、S⊥轴线、∥正面 ◎与半圆柱面交线 圆弧 回主视图 实形 回左、俯视图 直线 ◆P、Q∥轴线、 ∥侧 ⊙与半圆柱交线 一直线 ⊙左视图 实形 ©主、俯视图 直线 ★ 作图 ◆ 画出截切前完整的左视图 ◆ 画出P、Q、T、S在主、左视图的投影 加粗轮廓线 ●
例4 已知俯视图、部分主视图,求左视图。 ★ 分析 ◆半圆柱被四个平面截切 左右对称 ◆T、S⊥ 轴线、∥正面 ◎与半圆柱面交线——圆弧 ◎主视图——实形 ◎左、俯视图——直线 ◆P、Q∥轴线、∥侧面 ◎与半圆柱交线——直线 ◎左视图—— 实形 ◎主、俯视图——直线 ★ 作图 ◆画出截切前完整的左视图 ◆画出P、Q、T、S在主、左视图的投影 ◆加粗轮廓线 t p q s
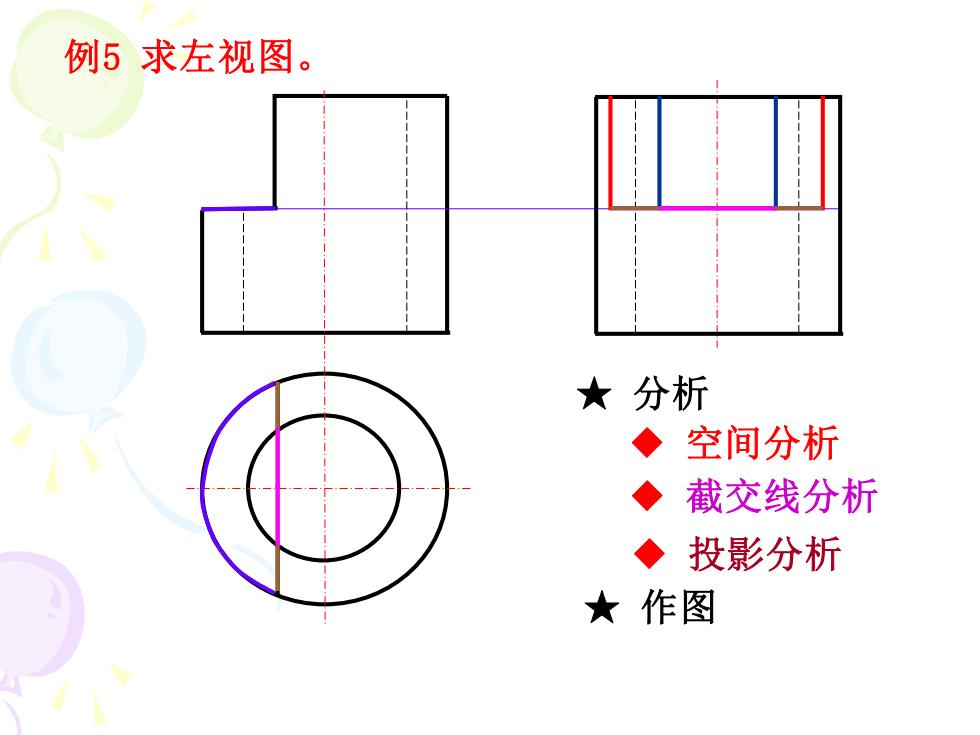
例5求左视图。 ★分析 ◆空间分析 ◆截交线分析 ◆投影分析 ★作图
例5 求左视图。 ◆ 空间分析 ◆ 截交线分析 ◆ 投影分析 ★ 分析 ★ 作图