
第二章 立体与立体表面交线 相贯线的画法
第二章 立体与立体表面交线 相贯线的画法
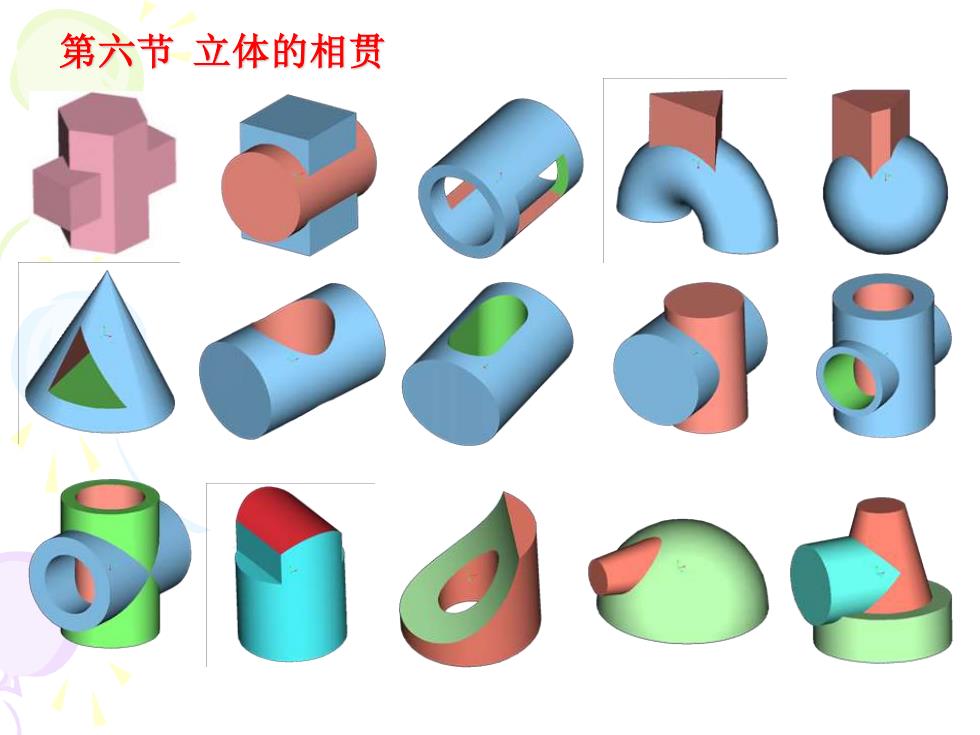
第六节立体的相贯
第六节 立体的相贯
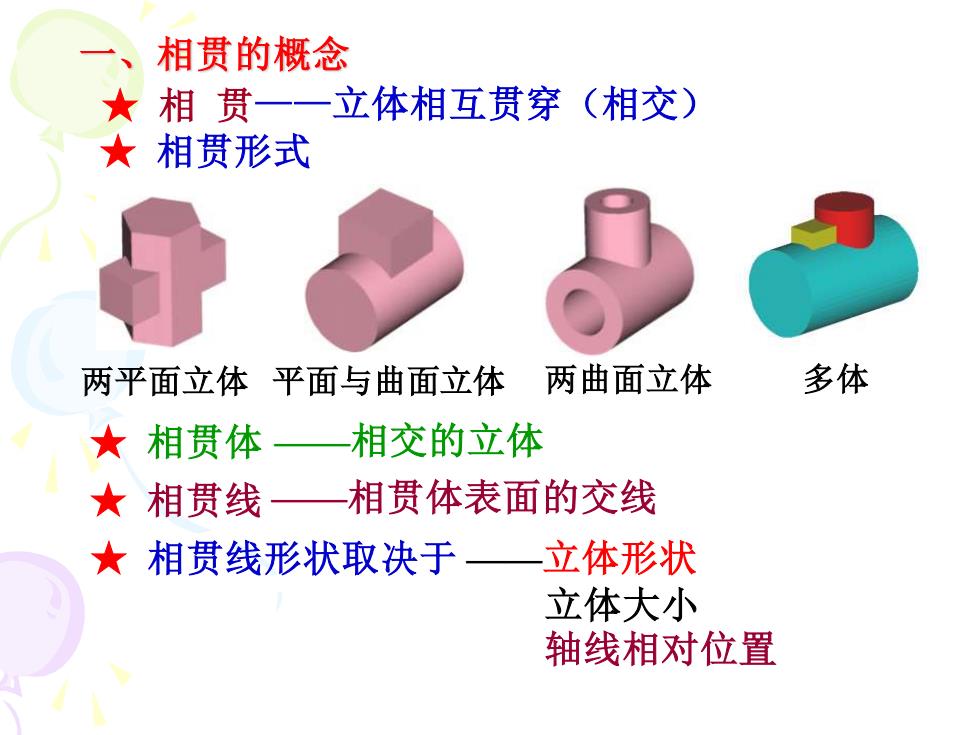
一、相贯的概念 ★相贯一一立体相互贯穿(相交) ★相贯形式 两平面立体平面与曲面立体 两曲面立体 多体 ★相贯体 相交的立体 女相贯线—相贯体表面的交线 ★相贯线形状取决于 一立体形状 立体大小 轴线相对位置
★ 相贯体 ——相交的立体 ★ 相贯线 ——相贯体表面的交线 ★ 相贯线形状取决于 ——立体形状 立体大小 轴线相对位置 一、相贯的概念 两平面立体 平面与曲面立体 两曲面立体 多体 ★ 相 贯——立体相互贯穿(相交) ★ 相贯形式

★相贯线主要性质 ◆表面性一一于立体表面 ◆ 封闭性一一封闭空间折线或曲线 ◆共有性 立体表面共有点的集合(共有线) 画相贯线的实质 求相贯体表面若干共有点的投影
★ 相贯线主要性质 ◆ 表面性——于立体表面 ◆ 封闭性——封闭空间折线或曲线 ◆ 共有性——立体表面共有点的集合(共有线) 画相贯线的实质 求相贯体表面若干共有点的投影

二、平面立体与平面立体相贯 习题集 P41,17 例1已知主、俯视图,求作侧视图。 ★五棱柱开三角形孔 ★求相贯线 ★加深 关键 求棱线与侧棱面的交点
二、平面立体与平面立体相贯 例1 已知主、俯视图,求作侧视图。 ● ● ★ 五棱柱开三角形孔 ★ 求相贯线 ★ 加深 关键——求棱线与侧棱面的交点 习题集 P41,17
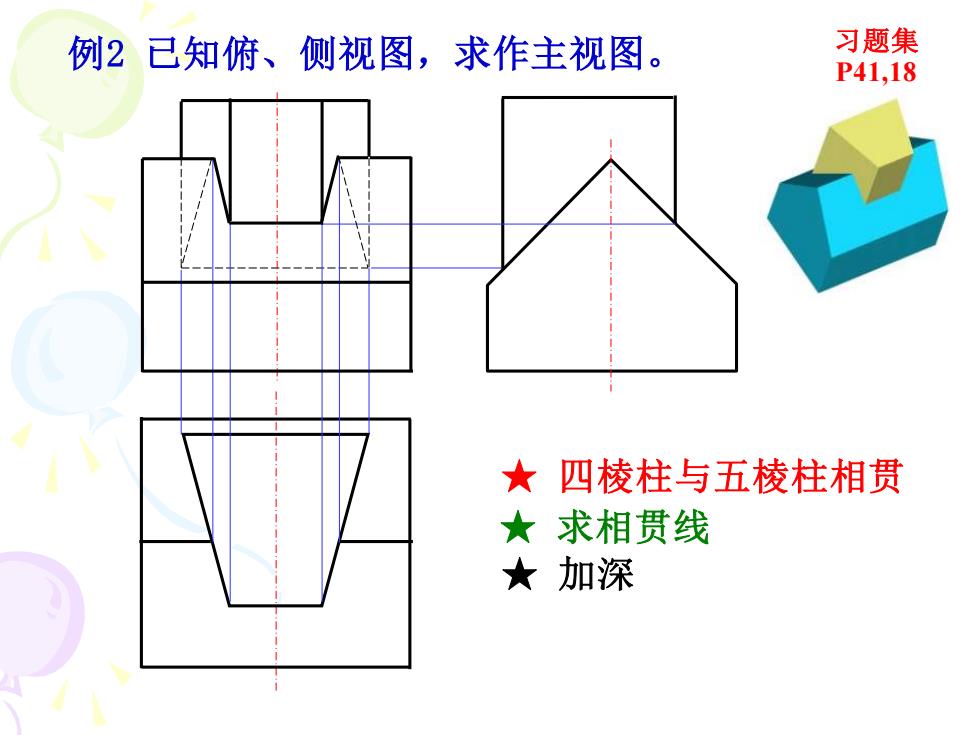
例2已知俯、侧视图,求作主视图。 习题集 P41,18 ★四棱柱与五棱柱相贯 ★求相贯线 ★加深
例2 已知俯、侧视图,求作主视图。 ★ 四棱柱与五棱柱相贯 ★ 求相贯线 ★ 加深 习题集 P41,18
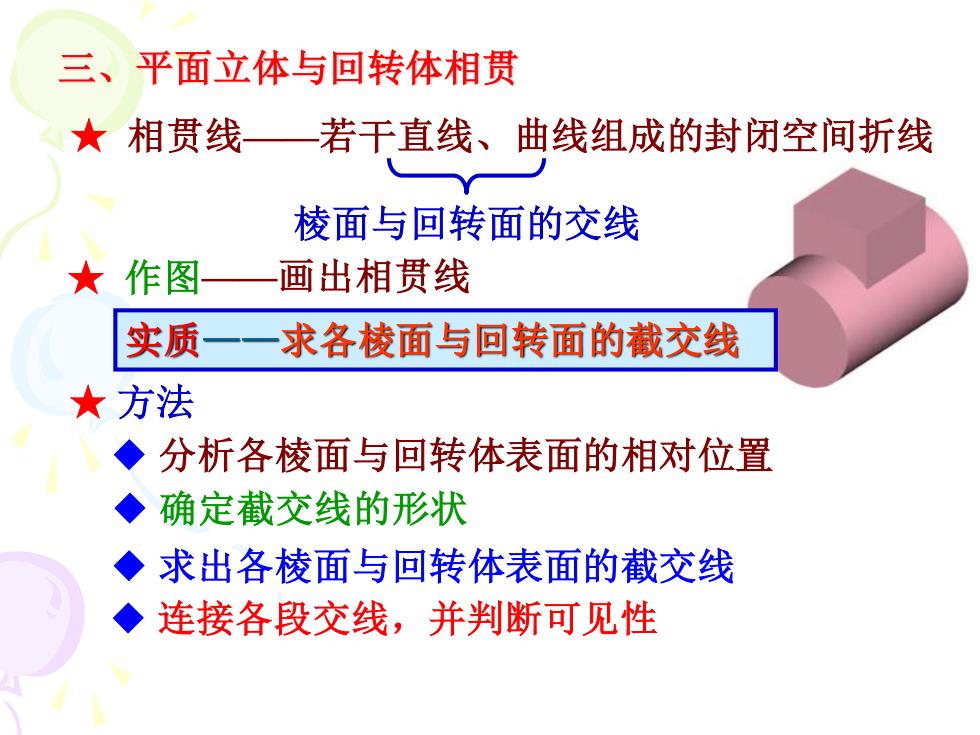
三、平面立体与回转体相贯 ★相贯线— 若干直线、曲线组成的封闭空间折线 棱面与回转面的交线 ★作图 画出相贯线 实质 求各棱面与回转面的截交线 ★方法 ◆分析各棱面与回转体表面的相对位置 ◆确定截交线的形状 ◆求出各棱面与回转体表面的截交线 ◆ 连接各段交线,并判断可见性
★ 相贯线——若干直线、曲线组成的封闭空间折线 ★ 作图 ◆ 分析各棱面与回转体表面的相对位置 ◆ 求出各棱面与回转体表面的截交线 ◆ 连接各段交线,并判断可见性 实质——求各棱面与回转面的截交线 三、平面立体与回转体相贯 ——画出相贯线 ★ 方法 ◆ 确定截交线的形状 棱面与回转面的交线

例3四棱柱与圆柱相交, 已知俯、左视图,作主视图。 ★分析 ◆相贯线一四柱面与圆柱面的交线 回前后柱面∥圆柱轴线→直线段 ©左右柱面⊥圆柱轴线→圆弧 ⊙侧投影—圆弧 主视方向 回水平投影 矩形 前后柱面∥V面→实形 ★作图 ◆主视图 与俯视图 长对正 与左视图 高平齐 前后棱面的投影
主视方向 例3 四棱柱与圆柱相交,已知俯、左视图,作主视图。 ★ 分析 ◆相贯线——四柱面与圆柱面的交线 ◎前后柱面∥圆柱轴线 ◎左右柱面⊥圆柱轴线 ◆ 前后柱面∥V面 →实形 ★ 作图 ◆主视图 与左视图——高平齐 与俯视图——长对正 前后棱面的投影 ◎侧投影——圆弧 ◎水平投影——矩形 →直线段 →圆弧
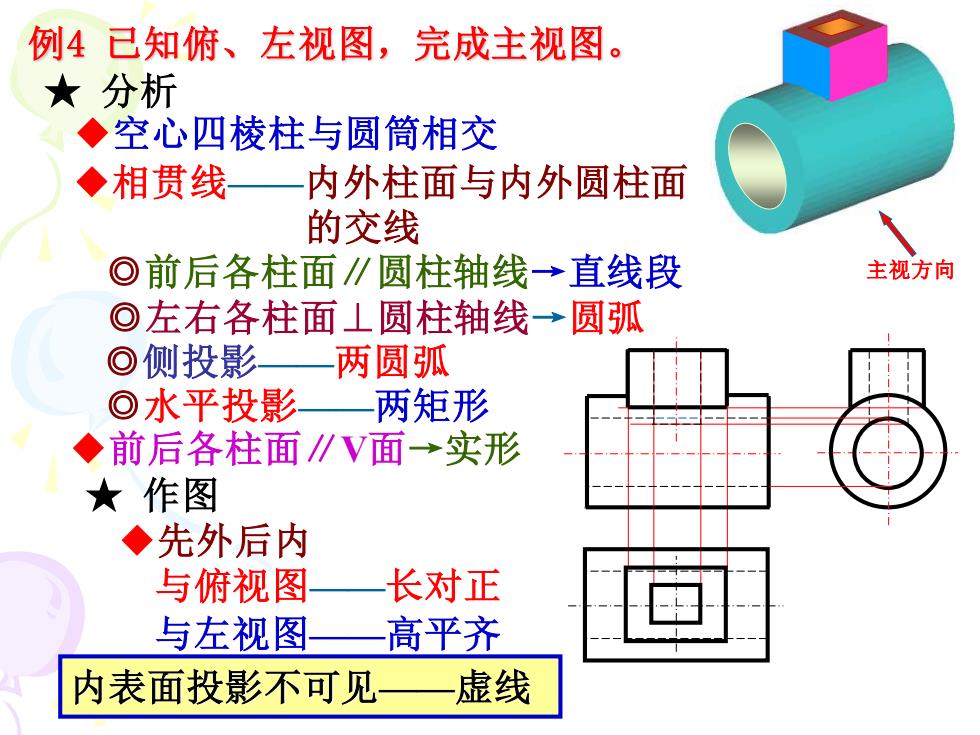
例4已知俯、左视图,完成主视图。 ★分析 ◆空心四棱柱与圆筒相交 ◆相贯线— 内外柱面与内外圆柱面 的交线 ◎前后各柱面∥圆柱轴线→直线段 主视方向 ©左右各柱面⊥圆柱轴线→圆弧 O侧投影 两圆弧 ⊙水平投影 两矩形 ◆前后各柱面∥V面→实形 ★作图 ◆先外后内 与俯视图 长对正 与左视图 高平齐 内表面投影不可见 虚线
★ 分析 ◆相贯线——内外柱面与内外圆柱面 的交线 ◎前后各柱面∥圆柱轴线→直线段 ◎左右各柱面⊥圆柱轴线→圆弧 ◆前后各柱面∥V面→实形 ★ 作图 ◆先外后内 与左视图——高平齐 与俯视图——长对正 内表面投影不可见——虚线 例4 已知俯、左视图,完成主视图。 ◆空心四棱柱与圆筒相交 ◎侧投影——两圆弧 ◎水平投影——两矩形 主视方向
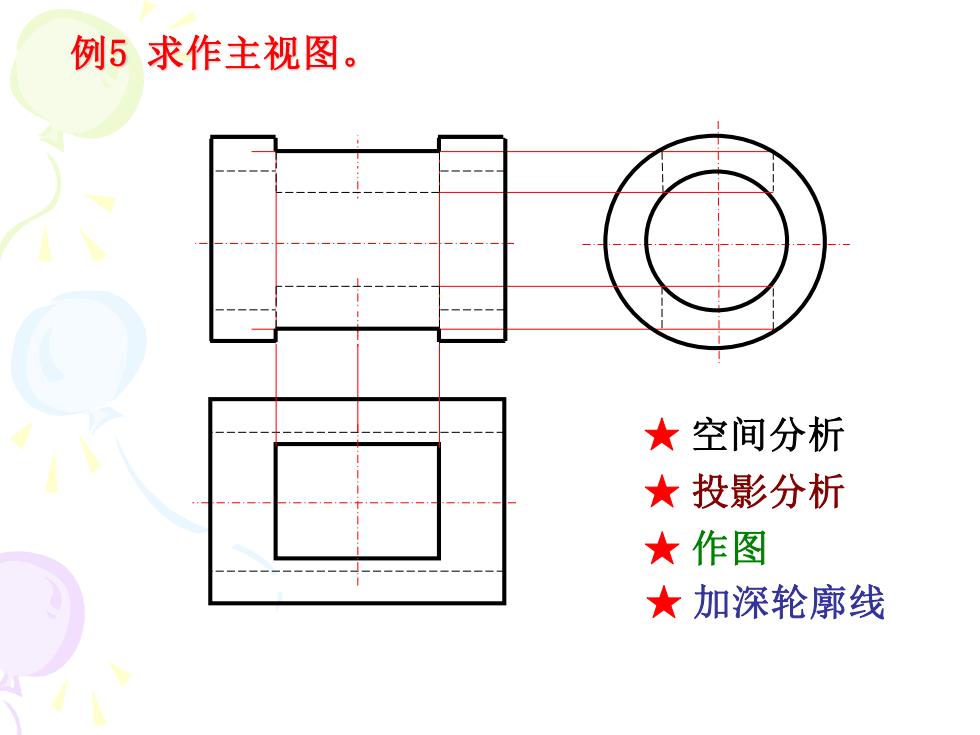
例5求作主视图。 女空间分析 ★投影分析 ★作图 ★加深轮廓线
例5 求作主视图。 ★ 空间分析 ★ 投影分析 ★ 作图 ★ 加深轮廓线