天津科技大学：《无机化学与分析化学》课程教学资源（教案讲义）第二章 化学反应的一般原理

第二章化学反应的一般原理 第二章化学反应的一般原理 一、 教学基本要求 了解体系、环境、状态、状态函数、热力学能、热、功：理解热力学第一定律 2.热化学 熟悉恒容反应热、恒压反应热、焓、标准摩尔反应焓变、标准摩尔生成焓等基本概 念；掌握盖斯定律的应用、热化学反应方程式的正确书写、掌握由标准摩尔生成焓计算标准 摩尔反应焓变的方法。 3.化学反应的方向 熟悉熵、吉布斯函数的概念。掌握标准摩尔反应熵变及标准摩尔反应吉布斯函数变 的计算方法。会用△G判定反应方向。 4.化学平衡及其移动 熟悉化学平衡的概念及实验平衡常数：掌握标准平衡常数及其有关计算；掌握多重平 衡规则；掌握化学平衡移动的规律。（浓度、压力、温度、催化剂等对平衡的影响） 5.化学反应速率 解化学反应速率的概念，理解化学反应速率方程表达式和反应级数的概念：理解阿仑 尼乌斯公式及其应用，比如求和速率常数：理解碰撞理论、过渡态理论及浓度、温度、催 化剂对反应速率的影响。 二、学时安排 教学内容 学时 1.基本概念和术语 1学时 2.热化学 2学时 3.化学反应的方向 2学时 4.化学平衡及其移动 2学时 5.化学反应速率 2学时 三、教学内容 §2-1，基本概念和术语 一、体系和环境 体系一 一人为选取一定种类，一定数量的物质作为研究的对象，这一部分物质或空间叫做 体系或系 环境 与体系有密切联系的一部分物质或空间。 二、状态和状态函数 1、状本 由一系列表征系统性质的宏观物理量（如T、P、V等）所确定下来的系统的存在形式称 系统的状态 一个体系的状态是由它的一系列物理量来确定的。这些物理量我们称之为体系的宏观性

第二章 化学反应的一般原理 8 第二章 化学反应的一般原理 一、 教学基本要求 1．基本概念和术语 初步了解体系、环境、状态、状态函数、热力学能、热、功；理解热力学第一定律。 2．热化学 熟悉恒容反应热、恒压反应热、焓、标准摩尔反应焓变、标准摩尔生成焓等基本概 念；掌握盖斯定律的应用、热化学反应方程式的正确书写、掌握由标准摩尔生成焓计算标准 摩尔反应焓变的方法。 3．化学反应的方向 熟悉熵、吉布斯函数的概念。掌握标准摩尔反应熵变及标准摩尔反应吉布斯函数变 的计算方法。会用ΔG 判定反应方向。 4．化学平衡及其移动 熟悉化学平衡的概念及实验平衡常数；掌握标准平衡常数及其有关计算；掌握多重平 衡规则；掌握化学平衡移动的规律。（浓度、压力、温度、催化剂等对平衡的影响） 5．化学反应速率 解化学反应速率的概念，理解化学反应速率方程表达式和反应级数的概念；理解阿仑 尼乌斯公式及其应用，比如求 Ea 和速率常数；理解碰撞理论、过渡态理论及浓度、温度、催 化剂对反应速率的影响。 二、学时安排 教 学 内 容 学 时 1．基本概念和术语 1 学时 2．热化学 2 学时 3．化学反应的方向 2 学时 4．化学平衡及其移动 2 学时 5．化学反应速率 2 学时 三、教学内容 §2-1，基本概念和术语 一、体系和环境 体系——人为选取一定种类，一定数量的物质作为研究的对象，这一部分物质或空间叫做 体系或系统。 环境——与体系有密切联系的一部分物质或空间。 二、状态和状态函数 1、 状态 由一系列表征系统性质的宏观物理量（如 T、P、V 等）所确定下来的系统的存在形式称 系统的状态。 一个体系的状态是由它的一系列物理量来确定的。这些物理量我们称之为体系的宏观性

第二章化学反应的一般原理 9 质。可分为容量性质和强度性质。 容量性质：与物质的数量有关，具有加合性。如m、V、n、Cr(热容量) 强度性质：与物质的数量无关，不具有加合性。如T、P、P、C(比热) 当体系的宏观性质都有确定值时， 我们称其处于 一定的状态 ,体系的任何一个性质发生变化 时，体系的状态即改变。但状态改变时，不一定所有的性质都改变。 2、状态函数 凡能决定体系状态的一切宏观性质（物理量）都叫做状态函数。 特点： <>体系的一些状态函数是相互联系、相互制约的。因此确定了几个状态函数，其它的 状态函数也随之而定。如PV=nRT 任何状态函数的变化值，只决定于体系的始态和终态。而与变化的途径无关。 10℃ 1) △ 30℃ (2)△ 冷却 500 (3) 冷却 4 0℃ 如：一杯水经①、②、③三个不同的途径，由10℃变成30℃，虽途径不同但△T=30℃ -10℃=20℃ 定换言之：如果一个物理量的变化值，只与体系的始末状态有关而与变化的途径无关，它 状态函数的这一特性，使研究得以简化。可不考虑其复杂的中间过程，直接求出状态函 数的变化量。 二、 热和功 热和功是系统发生状态变化时与环境进行能量交换的两种形式 热(Q):由于温度不同而造成的能量的传递。 功(W):除热之外，所有其他形式的能量传递。 「体积功 非体积功 *Q和W不是状态函数 Q和W是体系发生变化时能量的传递形式。只有在体系发生变化时才显示出来。不是体 系所具有的性质。他们除与体系状态有关外还与变化的具体途径有关。 *Q和W的符号 「体系吸热为“+” 环境对体系做功为“+” Q 体系放热为“一” 体系对环境做功为“” 三、热力学能与热力学第一定律 i.热力学能(U) 定义：体系内部能量的总和，（包括分子的动能、势能、键能、核能等）不包括体系整体

第二章 化学反应的一般原理 9 质。可分为容量性质和强度性质。 容量性质：与物质的数量有关，具有加合性。如 m、V、n、Cr(热容量)。 强度性质：与物质的数量无关，不具有加合性。如 T、P、ρ、C（比热） 当体系的宏观性质都有确定值时，我们称其处于一定的状态。体系的任何一个性质发生变化 时，体系的状态即改变。但状态改变时，不一定所有的性质都改变。 2、 状态函数 凡能决定体系状态的一切宏观性质（物理量）都叫做状态函数。 特点： 体系的一些状态函数是相互联系、相互制约的。因此确定了几个状态函数，其它的 状态函数也随之而定。如 PV=nRT 任何状态函数的变化值，只决定于体系的始态和终态。而与变化的途径无关。 10℃ (1 ) △ 30℃ （2） △ 冷却 50℃ （3） 冷却 △ 0℃ 如：一杯水经①、②、③三个不同的途径，由 10℃变成 30℃，虽途径不同但△T=30℃ －10℃=20℃ 换言之：如果一个物理量的变化值，只与体系的始末状态有关而与变化的途径无关，它 一定是个状态函数。 状态函数的这一特性，使研究得以简化。可不考虑其复杂的中间过程，直接求出状态函 数的变化量。 二、 热和功 热和功是系统发生状态变化时与环境进行能量交换的两种形式。 热（Q）：由于温度不同而造成的能量的传递。 功（W）：除热之外，所有其他形式的能量传递。    非体积功 体积功 * Q 和 W 不是状态函数 Q 和 W 是体系发生变化时能量的传递形式。只有在体系发生变化时才显示出来。不是体 系所具有的性质。他们除与体系状态有关外还与变化的具体途径有关。 * Q 和 W 的符号 Q    + 体系放热为“—” 体系吸热为“ ” W    − + 体系对环境做功为“ ” 环境对体系做功为“ ” 三、 热力学能与热力学第一定律 i.热力学能（U） 定义：体系内部能量的总和，（包括分子的动能、势能、键能、核能等）不包括体系整体

第二章化学反应的一般原理 10 运动的动能和体系整体处于外力场中具有的位能。 热力学能是状态函数，一定的状态下有一定的U值，同一体系、同一状态时，不可能有 不同的U值。而不同体系或同一体系不同状态时则可能有相同的U值。 U的绝对数值是不可求的，只能测出反应前后U的变化值△U △U=U一U U、P、V均为状态函数，“H也是状态函数 ∴格的变化量△H只与始态与终态有关，与途径无关。 △H=H悠一H# 在恒压不作非体积功的条件下，Q=△H ,U的绝对值不可测，H的绝对值也不可测，但可以通过恒压反应热求出：△H=QP 烙是体系的容量性质，具有加合性。 焓变：：△H=QP.△H与Qp的符号相同，吸热为“+”，放热为“ 反应的△H受温度的影响比较小，故可用298K下的△H代替其它温度下的△H。 ·.·AU=O+WO=AIJ-W 在恒压及不做非体积功的条件下：Q=△U十P△V=△H 在反应物和生成物都是周态和液态时，反应的△V很小，P△V可以忽略 ,故△H≈△U 在有气体参与的反应中，P△V=△nRT,则△H=△U+△nRT(△n为气体摩尔数的变化量.)

第二章 化学反应的一般原理 10 运动的动能和体系整体处于外力场中具有的位能。 热力学能是状态函数，一定的状态下有一定的 U 值，同一体系、同一状态时，不可能有 不同的 U 值。而不同体系或同一体系不同状态时则可能有相同的 U 值。 U 的绝对数值是不可求的，只能测出反应前后 U 的变化值ΔU。 ΔU=U 终－U 始 U 为容量性质，具有加合性，采用能量单位：J 或 kJ。 ii. 热力学第一定律（能量守恒定律） 定律：在任何过程中，能量不会自生自灭，只能从一种形式转化为另一种形式。转化过程中， 能量的总值不变。 数学表达式：ΔU－（Q＋W）=0 即：ΔU=Q＋W §2-2 热化学 一、化学反应的热效应（反应热） 定义：系统发生化学变化时，当系统不作非体积功，并使体系终态温度恢复到始态温度， 则在这一过程中放出或吸收的热量称为该反应的反应热。 1．恒容反应热 在不作非体积功的情况下，恒容过程的 V 终=V 始 即ΔV=0 体积功 W=PΔV=0 则ΔU=QV 即：恒容过程中体系所吸收的能量 QV 全部用来增加体系的内能。 2．恒压反应热 恒压过程通常是在敞口容器中进行的。P 终=P 始=P 外 由于体系只做体积功，∴W=－PΔV，则ΔU=QP－PΔV 3．体系的焓与反应的焓变 焓：在恒压和不作非体积功的条件下，由能量守恒定律， ΔU= QP－PΔV QP=ΔU＋PΔV=U2－U1＋P(V2－V1)=( U2＋P V2)－(U1＋P V1) 两括号中的内容相同，且均为状态函数(状态 2－状态 1 )，因此人为定义出一个新的状态 函数焓（H）。 定义：H=U+PV ∵U、P、V 均为状态函数，∴H 也是状态函数。 ∴焓的变化量ΔH 只与始态与终态有关，与途径无关。 ΔH=H 终－H 始 在恒压不作非体积功的条件下，QP=ΔH ∵U 的绝对值不可测，∴H 的绝对值也不可测，但可以通过恒压反应热求出：ΔH= QP 焓是体系的容量性质，具有加合性。 焓变：∵ΔH= QP ∴ΔH 与 Qp 的符号相同，吸热为“+”，放热为“—”。 反应的ΔH 受温度的影响比较小，故可用 298K 下的ΔH 代替其它温度下的ΔH。 ∵ΔU= Q+W Q=ΔU—W 在恒压及不做非体积功的条件下：QP=ΔU＋PΔV=ΔH 在反应物和生成物都是固态和液态时，反应的ΔV 很小，PΔV 可以忽略，故ΔH≈ΔU 在有气体参与的反应中，PΔV=△nRT，则ΔH=ΔU＋△nRT （△n 为气体摩尔数的变化量。）

第二章化学反应的一般原理 例21在256100,11帝完全烧尿孩 解 恒正进行的，》下以该反应的 △g= 1,R=8314JKo 298.150 A=人H△GR7 367-11831429815101T 364 上面所讲的两个关系式：△U=Qy:AH=Q 热不是状态函数，但由于Qv对应△U,QP对应△H。所以在这两种特殊情况下，Qy、QP 只与始态和终态有关。与变化的途径无关。 二、盖斯定律 反应的热效应可以由实验测得，但化学反应成千上万，逐一测定很困难。而且有些热效 应实际上很难 不能测出。 如：(1)C(石墨)+02(g)-→C02(g)△，Hm1=-393.5kJ·mol厂1 (2)C(石墨)+102(g)-→C0g) △Hm2 在第二个反应进行的过程中，总会有一部分CO2生成，所以实际上△Hm2不能准确测出 因此在1840 俄国化学家 盖斯在大量试验的基础上得出了著名的热化学 盖斯定律 定律：在整个过程处于恒容或恒压情况时，化学反应的热效应只与始、终状态有关，而与变 化的途径无关。 另一种说法：在恒容或恒压条件下，一个化学反应无论是一步完成，还是分成几步完成， 其总反应的反应热等与各步反应热之和。 上面所讲的第2个反应，则可根据盖斯定律求出。 写出相关的第三个反应式：C0g)+0:g)一一C0:g) △H3=-283.0kJ·mol1 C(石墨) 02 4→C02(g) △H △H3 cog)+02(g) (1)C(石墨)+02(g)-→C02(g) 一) (2)C0(g)+502(g)-→C02(g) (3)C(石墨)十02(g→C0(g) 即：反应(1)=反应(2)+反应(3) 反应(2)=反应(1)一反应(3)则AH=△H1-△H △H2=-393.5-(-283.0)=-110.5kJ·mol1 ∴热化学方程式也和代数方程式一样可以进行加减运算或乘以系数，而其反应的热效应也应 进行相应的运算

第二章 化学反应的一般原理 11 上面所讲的两个关系式：ΔU=QV ；ΔH= QP 热不是状态函数，但由于 QV 对应ΔU，QP 对应ΔH。所以在这两种特殊情况下，QV 、QP 只与始态和终态有关。与变化的途径无关。 二、盖斯定律 反应的热效应可以由实验测得，但化学反应成千上万，逐一测定很困难。而且有些热效 应实际上很难或不能测出。 如：（1）C（石墨）＋O2 (g)－→CO2(g) ΔrHm1=－393.5kJ·mol－1 (2 ) C (石墨)＋ 2 1 O2 (g)—→CO(g) ΔrHm2 在第二个反应进行的过程中，总会有一部分 CO2 生成，所以实际上ΔrHm2 不能准确测出。 因此在 1840 年，俄国化学家盖斯在大量试验的基础上得出了著名的热化学定律—盖斯定律。 定律：在整个过程处于恒容或恒压情况时，化学反应的热效应只与始、终状态有关，而与变 化的途径无关。 另一种说法：在恒容或恒压条件下，一个化学反应无论是一步完成，还是分成几步完成， 其总反应的反应热等与各步反应热之和。 上面所讲的第 2 个反应，则可根据盖斯定律求出。 写出相关的第三个反应式：CO(g)＋ 2 1 O2 (g) —→CO2(g) ΔH3=－283.0kJ·mol－1 C（石墨） ＋ O2 ⎯⎯H1→ CO2(g) ΔH2 ΔH3 CO(g)＋ 2 1 O2 (g) （1）C（石墨）＋O2 (g)－→CO2(g) —） （2）CO(g)＋ 2 1 O2 (g) —→CO2(g) （3） C (石墨)＋ 2 1 O2 (g)—→CO(g) 即：反应（1）=反应（2）＋反应（3） 反应（2）=反应（1）－反应（3）则ΔH2=ΔH1－ΔH3 ΔH2=－393.5－（－283.0）=－110.5 kJ·mol－1 ∴热化学方程式也和代数方程式一样可以进行加减运算或乘以系数，而其反应的热效应也应 进行相应的运算

第二章化学反应的一般原理 12 三、标准摩尔反应焓变 1、摩尔反应焓变（△rHm) 个反应的反应格变，其大小与反应进度ξ有关 △rHm的定义：某化学反应按所给定的化学计量方程式反应，当反应进度=lmol时的 反应焓变称为摩尔反应焓变。 即：△rHm=△，H J·mol或kJ·mol 下标中r为反应(reaction)的意思，m为反应进度lmol之意， 2、物质的标准态和标准摩尔焓变。△rH。 p°：100kPac°：1mol1L1T:298.15K 在标准态时反应的摩尔焓变称为反应的标准摩尔焓变△H 3、热化学反应方程式 表示化学反应与其热效应关系的化学方程式称为热化学反应方程式。在化学反应式后用 △rH。表示反应的热效应。（指恒压下的反应热） 要求： )应注明物质的聚集状态，5、1、g,固体有多种晶型时还应注明晶型。如：石墨和金刚 石，聚集状态不同，△rH不同。 2)应正确写出化学反应计量式，即同一反应，其反应式计量系数不同时，△rH“也不同（见 书P19(4式、(5)式) 3)注明反应温度，标准态(298.15K时)不需注明。 4.标准摩尔生成焓（△rH) 标准生成焓：在标准状态下，由稳定单质生成1mol纯物质时反应的摩尔焓变，成为该 物质的标准摩尔生成焓△rH:。下标f为生成反应(formation)的意思。即在标准状态下， 种特定反应（生成反应）的产物只有一种，而且产物的计量系数为1时，反应的标准摩尔焓 由定义可以得出：稳定单质的△H=0 如△H"C(石墨)=0 △rHC(金刚石)=189kJ·mol1白磷：△rH=0 书后附录三中列出各物质及水合离子的△H a)由△rH计算△rH:利用书后△cH数据可简化反应热的计算： 例：计算反应3C0(g)+Fe2O3(s)→2Fe+3C02(g)的△rH(298)

第二章 化学反应的一般原理 12 三、标准摩尔反应焓变 1、摩尔反应焓变（△rHm） 一个反应的反应焓变，其大小与反应进度 ξ 有关。 ΔrHm 的定义：某化学反应按所给定的化学计量方程式反应，当反应进度 ξ=1mol 时的 反应焓变称为摩尔反应焓变。 即：ΔrHm=  r H J·mol－1 或 kJ·mol－1 下标中 r 为反应（reaction）的意思，m 为反应进度 1mol 之意。 2、物质的标准态和标准摩尔焓变。Δr  H m p  ：100kPa  c ：1mol·L －1 T：298.15K 在标准态时反应的摩尔焓变称为反应的标准摩尔焓变 Δr  H m 3、热化学反应方程式 表示化学反应与其热效应关系的化学方程式称为热化学反应方程式。在化学反应式后用 Δr  H m 表示反应的热效应。（指恒压下的反应热） 要求： 1) 应注明物质的聚集状态，s、l、g，固体有多种晶型时还应注明晶型。如：石墨和金刚 石，聚集状态不同，Δr  H m 不同。 2) 应正确写出化学反应计量式，即同一反应，其反应式计量系数不同时，Δr  H m 也不同（见 书 P19 (4) 式、（5）式） 3) 注明反应温度，标准态（298.15K 时）不需注明。 4．标准摩尔生成焓（Δf  H m ） 标准生成焓：在标准状态下，由稳定单质生成 1mol 纯物质时反应的摩尔焓变，成为该 物质的标准摩尔生成焓 Δf  H m 。下标 f 为生成反应（formation）的意思。即在标准状态下，一 种特定反应（生成反应）的产物只有一种，而且产物的计量系数为 1 时，反应的标准摩尔焓 变。 由定义可以得出：稳定单质的 Δf  H m =0 如 Δf  H m C（石墨）=0 Δf  H m C（金刚石）=1.89 kJ·mol－1 白磷：Δf  H m =0 书后附录三中列出各物质及水合离子的 Δf  H m a) 由 Δf  H m 计算 Δr  H m ：利用书后 Δf  H m 数据可简化反应热的计算： 例：计算反应 3CO(g)＋Fe2O3(s) ⎯` → 2Fe＋3CO2(g)的 Δr  H m (298)

第二章化学反应的一般原理 解：对于任何一个反应均可写成如下的循环： 3C0(g)+ Fe2O3(s) 成→ 2Fe+3C02(g) Ar H (ve) 3△rH(CO) △rHA(Fe2O3) 3ArH (CO2) 3Cs)+302(g)+2Fe(s) 由盖斯定律，按循环方向有： 3ArH(C0)+△rH(Fe2O3)+△rH=2△rH(Fe)+3ArH8(CO2) 整理：△rH=△rH(FC)+3△rH(CO2)-3△rH:(CO)-△rH。(Fe2O3) 查书后附录找出各物质的△H即可求出反应的△rH:。 由于各反应式均可写出上述循环，故总结出通式： ArH=∑ya·4yHR(B) 由于反应物的化学计量系数为负值，可以写成 △rH=∑y,4H(产物)-∑y,·4H(反应物 利用上述通式计算时应注意： 1、要考虑反应式中各物质的聚集状态，如：△H(H2O,1)≠△H(HzO,g) 2、书后表中所给的数值均为生成1mol物质时的△rH,计算时要乘以相应的系数

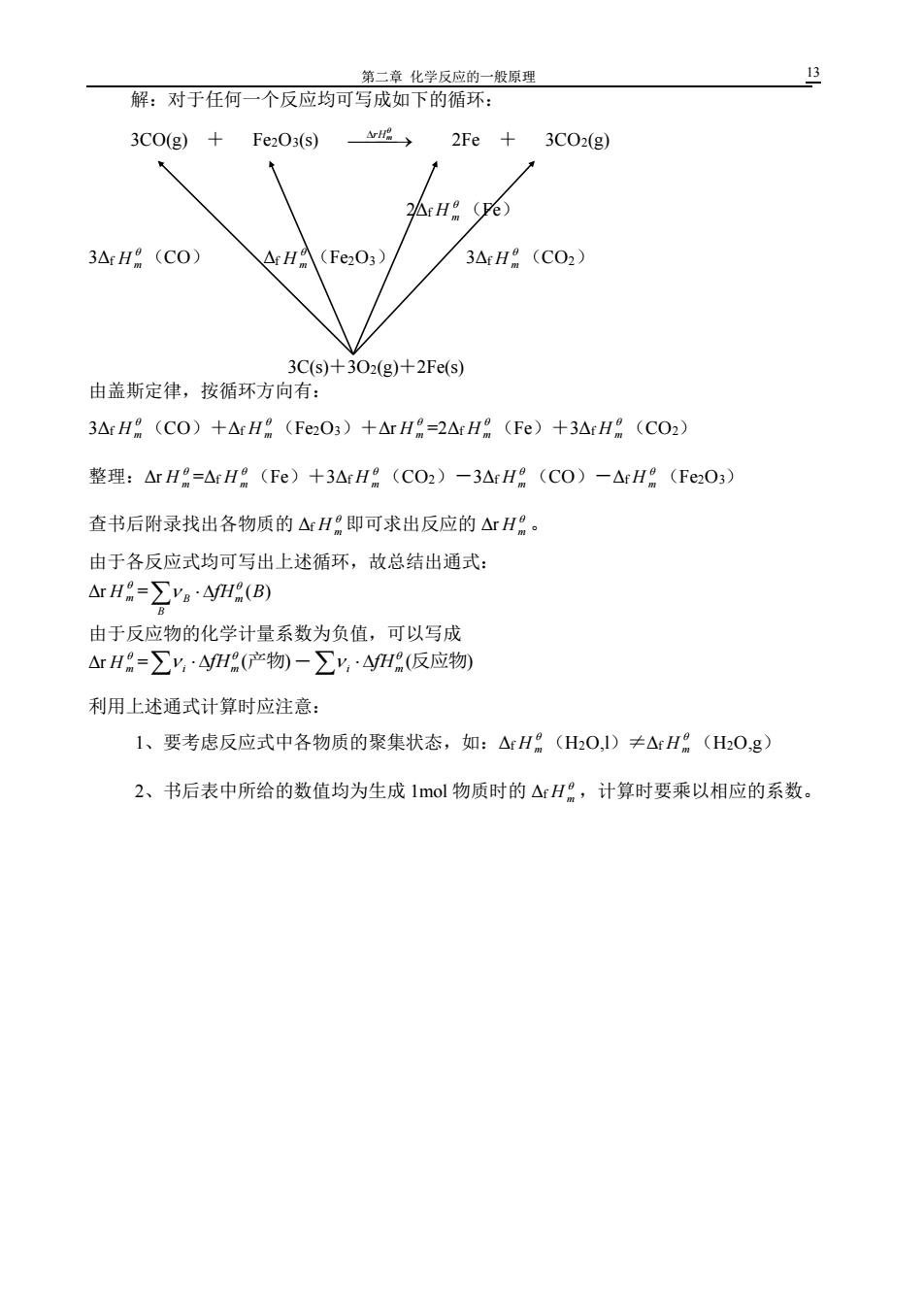
第二章 化学反应的一般原理 13 解：对于任何一个反应均可写成如下的循环： 3CO(g) ＋ Fe2O3(s) ⎯ ⎯→  rHm 2Fe ＋ 3CO2(g) 2Δf  H m （Fe） 3Δf  H m （CO） Δf  H m （Fe2O3） 3Δf  H m （CO2） 3C(s)＋3O2(g)＋2Fe(s) 由盖斯定律，按循环方向有： 3Δf  H m （CO）＋Δf  H m （Fe2O3）＋Δr  H m =2Δf  H m （Fe）＋3Δf  H m （CO2） 整理：Δr  H m =Δf  H m （Fe）＋3Δf  H m （CO2）－3Δf  H m （CO）－Δf  H m （Fe2O3） 查书后附录找出各物质的 Δf  H m 即可求出反应的 Δr  H m 。 由于各反应式均可写出上述循环，故总结出通式： Δr  H m =  B B fHm (B)   由于反应物的化学计量系数为负值，可以写成 Δr  H m =  (产物)   i m fH －  (反应物)   i m fH 利用上述通式计算时应注意： 1、要考虑反应式中各物质的聚集状态，如：Δf  H m （H2O,l）≠Δf  H m （H2O,g） 2、书后表中所给的数值均为生成 1mol 物质时的 Δf  H m ，计算时要乘以相应的系数

50 §23化学反应的方向 、化学反应的自发性 1、自发反应（或过程）：在一定条件下，不需要任何外力做功，就能自动进行的反应或 物理过程，称为自发反应式或自发过程。 如：水的流动、电流、0℃以下水的结冰。0℃以上冰的熔化，金属的生锈、及一些化学 反应，如：Zn十CuS04←→Cu十ZnS04 2、自发过程的推动力及限度 过程 自发方向 推动力 自发过程的最大 限度 水清 高水位低水位 △h △h-0 电流 高由位，低由位 气流 高气压一低气压 热传导 高温→低温 △T=0 化学反应 高自由焓→低自△G △G=0 由焓 结论： )自发变化的逆过程是非自发的 2)自发变化和非自发变化都是可能进行的，自发变化能自动进行，非自发变化需借 助一定方式的外部作用才能发生（如水泵、电解等）。 3)自发变化的最大限度是体系的平衡状态， 3、焓变与自发反应 自然界倾向于能量降低，如高位能→低位能、高温→低温，均属于能量降低，体系的能 量越低越稳定。 如：铁的生锈：3Fe(s)+202(g→Fe304(s) △rH2=-1118.4kJ·mol1 但单以能量降低为判据又不能解释如下事实：

第二章 化学反应的一般原理 14 §2-3 化学反应的方向 一、化学反应的自发性 1、自发反应（或过程）：在一定条件下，不需要任何外力做功，就能自动进行的反应或 物理过程，称为自发反应式或自发过程。 如：水的流动、电流、0℃以下水的结冰。0℃以上冰的熔化，金属的生锈、及一些化学 反应，如 ：Zn＋CuSO4 ⎯→ Cu＋ZnSO4 2、自发过程的推动力及限度 过程 自发方向 推动力 自 发 过程 的 最 大 限度 水流 高水位→低水位 Δh Δh=0 电流 高电位→低电位 ΔV ΔV=0 气流 高气压→低气压 Δp Δp=0 热传导 高温→低温 ΔT ΔT=0 化学反应 高 自 由焓 → 低 自 由焓 ΔG ΔG=0 结论： 1) 自发变化的逆过程是非自发的。 2) 自发变化和非自发变化都是可能进行的，自发变化能自动进行，非自发变化需借 助一定方式的外部作用才能发生（如水泵、电解等）。 3) 自发变化的最大限度是体系的平衡状态， 3、 焓变与自发反应 自然界倾向于能量降低，如高位能→低位能、高温→低温，均属于能量降低，体系的能 量越低越稳定。 如：铁的生锈：3Fe(s)＋2O2(g)—→Fe3O4（s） Δr  H m =－1118.4kJ·mol－1 但单以能量降低为判据又不能解释如下事实：

第二章化学反应的一般原理 H20S25C→H200 △rHR>0 KNO3(S)→K++NO △rH=35kJ·mol N205(g)→2N02(g)+，02(g) △rH2=56.7kJ·mol 还有些反应的自发性与温度有关。 如：CaC0ss)→Ca0(s)+C02(g) 此反应常温下不自发，而在850℃以上时，则能自发进行。 由此可见：用△H。S°B>SBS) 在定性判断一个化学反应是熵增还是嫡减时，通常考虑为气体分子数增大的方向 是嫡增过程。 温度：同一物质时，T>2则S”T>S卫 分子结构：分子量相近，结构越复杂，熵越大。对称性越好，熵越小。 如：S(C2HsOH)>S(CH-O-CH) 分子量：结构相近，分子量越大，熵越大。S°>S°m>S°H0>S° 2、标准摩尔反应熵变（△S)的计算 △rS的计算与由△H:计算△rH的形式相同。 △rS=∑ySg(产物)-∑yS(反应物)减4s=∑'aS2(B) 1)T对△rS的影响不大，在温度变化不是很大时，可用△rS(298)代替△rS(T) 2)稳定单质的S(298)≠0，查表时应注意

第二章 化学反应的一般原理 15 H2O(s) ⎯ ⎯C→ o 25 H2O(l) Δr  H m >0 KNO3(s) ⎯→ K ＋＋NO3 － Δr  H m =35 kJ·mol－1 N2O5(g) ⎯→ 2NO2(g)＋ 2 1 O2（g） Δr  H m =56.7 kJ·mol－1 还有些反应的自发性与温度有关。 如：CaCO3(s) ⎯→ CaO(s)＋CO2(g) 此反应常温下不自发，而在 850℃以上时，则能自发进行。 由此可见：用 Δr  H m  S B(l)>  S B(s) 在定性判断一个化学反应是熵增还是熵减时，通常考虑为气体分子数增大的方向 是熵增过程。 温度：同一物质时，T1>T2，则  S T1>  S T2 分子结构：分子量相近，结构越复杂，熵越大。对称性越好，熵越小。 如：  S （C2H5OH）>  S (CH3-O-CH3) 分子量：结构相近，分子量越大，熵越大。  S HI>  S HBr>  S HCl>  S HF 2、 标准摩尔反应熵变（Δr  m S ）的计算 Δr  m S 的计算与由 Δf  H m 计算 Δr  H m 的形式相同。 Δr  m S = i  m S （产物）－  i  m S (反应物)或 Δr  m S = B  B  m S （B） 1) T 对 Δr  m S 的影响不大，在温度变化不是很大时，可用 Δr  m S （298）代替 Δr  m S （T） 2) 稳定单质的  m S （298）≠0，查表时应注意

第二章化学反应的一般原理 3)单位：J·molI·K1 △S与△rH:一样，不能单独作为自发反应判断的依据。（如：0℃以下水自动结冰， 其△S。0不自发（逆反应自发） 标准状态下（各物质的C=1.0mol·L1,Pi=10OkPa)用△rG判断。非标态下应该用△rGm判 断。 3.标准摩尔生成自由焓 定义：标准状态下，由稳定单质生成1摩尔纯物质时，反应的自由焓变叫做该物质的标 准摩尔生成自由焓△G298) 稳定单质的△Gm=0。 4.△rG的计算 通式：△rG=∑y,A,G(产物-∑y,A,G(反应物 定义式：△rG=ArH-T△rS (常用于其它温度下的计算)

第二章 化学反应的一般原理 16 3) 单位：J·mol－1·K －1 Δr  m S 与 Δr  H m 一样，不能单独作为自发反应判断的依据。（如：0℃以下水自动结冰， 其 Δr  m S 0 不自发（逆反应自发） 标准状态下（各物质的 C=1.0mol·L －1 ,Pi=100kPa）用 Δr  Gm 判断。非标态下应该用 ΔrGm 判 断。 3．标准摩尔生成自由焓 定义：标准状态下，由稳定单质生成 1 摩尔纯物质时，反应的自由焓变叫做该物质的标 准摩尔生成自由焓 ΔfGm(298) 稳定单质的 ΔfGm =0。 4．Δr  Gm 的计算 通式：Δr  Gm = (产物)   i f Gm － (反应物)   i f Gm 定义式：Δr  Gm =Δr  H m －TΔr  m S (常用于其它温度下的计算)

第二章化学反应的一般原理 例：计算反应2H202(g)←→2H20(g)十02(g)在400K时的△rG 解：：T=400K∴.不能直接查△rG(298)代入公式计算，而应利用T对△rH、△rS影 响较小的特性，用定义式计算。 H202(g) H2O(g) 2(g) △rHe -131.31 -241.82 0 kJ·mol-1 232.60 188.72 205.03 J·molr1K △rH(298=2(-241.82)-2(-136.31F-211.02kJ·mo △rS0(298=2×188.72+205.03-2×232.60=117.23×103kJ·mo △rG°(400-211.02-400×117.23×103=-257.93kJ·mol1 266 5.压下，温度对反应自发性的影响 Ar H Ar S ArG=Ar H-TAr S 反应自发性 永远是 任何温度下，正反应都自发 + 永远是“+” 任何温度下，正反应都不自发 低温“一”：高温“十”低温自发，高温不自发 + 低温“十”：高温“一”低温不自发，高温自发 §2-4化学反应速率 一、反应速率的概今 反应速率的差异很大，有的瞬时完成，有的则看不到反应的发生。 应速率的表示方法：可用单位时间内任何一种反应物浓度的减少量或生成物浓度的增加量来

第二章 化学反应的一般原理 17 例：计算反应 2H2O2(g) ⎯→ 2H2O(g)＋O2(g) 在 400K 时的 Δr  Gm 解：∵T=400K ∴不能直接查 Δf  Gm (298)代入公式计算，而应利用 T 对 Δr  H m 、Δr  m S 影 响较小的特性，用定义式计算。 H2O2(g) H2O(g) O2(g) Δf  H m －131.31 －241.82 0 kJ·mol－1  m S 232.60 188.72 205.03 J·mol－1·K － 1 Δr  H m (298)=2(－241.82)－2(－136.31)=－211.02 kJ·mol－1 Δr  m S (298)=2×188.72＋205.03－2×232.60=117.23×10－3 kJ·mol－1 Δr  Gm (400)=－211.02－400×117.23×10－3=－257.93 kJ·mol－1 5． 压下，温度对反应自发性的影响 Δr  H m Δr  m S Δr  Gm =Δr  H m －TΔr  m S 反应自发性 － ＋ 永远是“－” 任何温度下，正反应都自发。 ＋ － 永远是“＋” 任何温度下，正反应都不自发。 － － 低温“－”；高温“＋” 低温自发，高温不自发 ＋ ＋ 低温“＋”；高温“－” 低温不自发，高温自发 §2-4 化学反应速率 一、 反应速率的概念 反应速率的差异很大，有的瞬时完成，有的则看不到反应的发生。 应速率的表示方法：可用单位时间内任何一种反应物浓度的减少量或生成物浓度的增加量来