
第一章分散系 返回主目录 返回次目录
返回主目录 返回次目录 1 第一章 分散系

1.1理想气体 ×1.2 溶浪 ×1.3精喀液的依数性 ×1.4 胶依喀液 ×1.5乳浊液和高分子喀液
1.1 理想气体 1.4 胶体溶液 1.3 稀溶液的依数性 1.2 溶液 1.5 乳浊液和高分子溶液

1.1理想气体 1.1.1 理想气体状态方程式 1.1.2 理想气体状态方程式的应用 1.1.3 分压定律 1.1.4分压定律的应用 3>*1.1.5分体积定律
1.1.1 理想气体状态方程式 1.1.2 理想气体状态方程式的应用 1.1 理想气体 1.1.3 分压定律 *1.1.5 分体积定律 1.1.4 分压定律的应用

1.1.1 理想气体状态方程式 气体的最基本特征: 具有可压缩性和扩散性。 人们将符合理想气体状态方程式的气体, 称为理想气体。 理想气体分子之间没有相互吸引和排斥, 分子本身的体积相对于气体所占有体积完全 可以忽略。 返回主目录 返回次目录
返回主目录 返回次目录 4 气体的最基本特征: 具有可压缩性和扩散性。 人们将符合理想气体状态方程式的气体, 称为理想气体。 理想气体分子之间没有相互吸引和排斥, 分子本身的体积相对于气体所占有体积完全 可以忽略。 1.1.1 理想气体状态方程式

理想气体状态方程式: pV=nRT R-摩尔气体常量 在STP下,p=101.325kPa, T=273.15K n=1.0mol时,Vm=22.414L=22.414×10-3m3 R- D 101325Pa×22.414×103m3 nT 1.0mol×273.15K =8.314J-mol-1.K-1 R=8.314 kPa-L.K-1.mol-1 返回主目录 返回次目录
返回主目录 返回次目录 5 pV = nRT R- 摩尔气体常量 在STP下,p =101.325kPa, T=273.15K n=1.0 mol时, Vm =22.414L=22.414×10-3m3 nT pV R = R=8.314 kPaLK-1 mol-1 理想气体状态方程式: 1 1 8.314J mol K − − = 3 3 101325Pa 22.414 10 m 1.0mol 273.15K − =

1.1.2 ,理想气体状态方程式的应用 1.计算p,V,T,n四个物理量之一。 pV=nRT 用于温度不太低,压力不太高的真实气体。 2.气体摩尔质量的计算 pV=nRT mRT M= M=M g.mol-1 返回主目录 返回次目录
返回主目录 返回次目录 6 1. 计算p,V,T,n四个物理量之一。 2.气体摩尔质量的计算 m n M = M = Mr gmol-1 1.1.2 理想气体状态方程式的应用 mRT M pV = m pV RT M = pV nRT = 用于温度不太低,压力不太高的真实气体。 pV = nRT
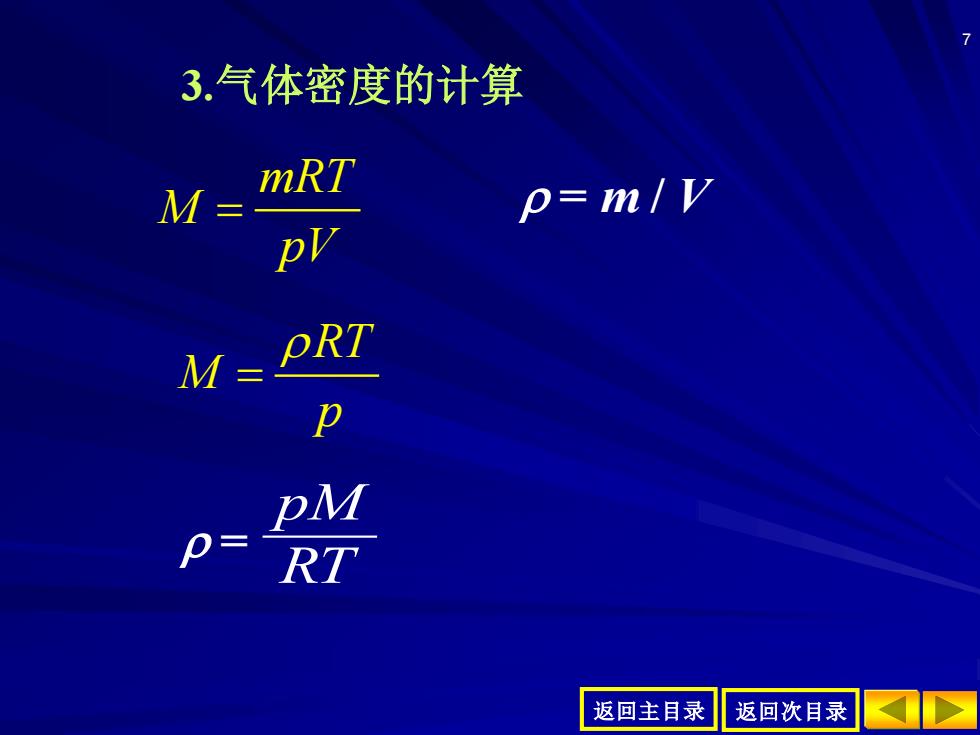
3.气体密度的计算 M= mRT p=m/y M= PRT p= 返回主目录 返回次目录
返回主目录 返回次目录 7 = RT pMmRT M pV = = m / V RT M p = 3.气体密度的计算

1.1.3 分压定律 组分气体: 理想气体混合物中每一种气体叫做组 分气体。 分压: 组分气体B在相同温度下占有与混合 气体相同体积时所产生的压力,叫做组分 气体B的分压。 HRT V 返回主目录 返回次目录
返回主目录 返回次目录 8 组分气体: 理想气体混合物中每一种气体叫做组 分气体。 分压: 组分气体B在相同温度下占有与混合 气体相同体积时所产生的压力,叫做组分 气体B的分压。 B B n RT p V = 1.1.3 分压定律

分压定律: 9 混合气体的总压等于混合气体中各组分 气体分压之和。 p=p1+p2+. 或 p=∑pB nRT n,RT P1= P2= nRT,nRT =+%+阿 n=n1+n2+ =2R 返回主目录 返回次目录
返回主目录 返回次目录 分压定律: 9 混合气体的总压等于混合气体中各组分 气体分压之和。 p = p1 + p2+ 或 p = pB V p = nRT = , = , 2 2 1 1 V n RT p V n RT p ( ) 1 2 1 2 n RT n RT RT p n n V V V = + + = + + n =n1+ n2+

10 分压的求解: DB nB RT nRT PB. 二 nB二XB n PB= 之 p=xuP xB一B的摩尔分数 返回主目录 返回次目录
返回主目录 返回次目录 10 分压的求解: x B ⎯ B的摩尔分数 V n RT p B B = B B B x n n p p = = V nRT p = B B B n p p x p n = =