
第七讲 从噪声中提取有用信息 。(1)叠加法改善信号质量的统计学依据 。(2)诱发脑电、希氏束电位和运动电位 的叠加方法 ,(3)用自相关法检测外周神经放电中的 周期性信号
第七讲 从噪声中提取有用信息 ⚫ (1)叠加法改善信号质量的统计学依据 ⚫ (2)诱发脑电、希氏束电位和运动电位 的叠加方法 ⚫ (3)用自相关法检测外周神经放电中的 周期性信号

确定性信号和随机信号 确定性信号 能通过一个确切地数学公式来描述, 能准确地予以预测。 例如正弦波信号 y(t)=Asin(ot+0)
确定性信号和随机信号 确定性信号 能通过一个确切地数学公式来描述, 能准确地予以预测。 例如正弦波信号 y(t) = Asin(t + )

随机信号 不能通过一个确切地数学公式来描述, 不能准确地予以预测。 常见的一种平稳随机信号有:各种无线电系统及电子装置中的噪声与干扰 生物医学信号,如心电图(ECG)脑电图(EEG)、肌电图(EMG)、心音图等 平稳随机信号 其均值与时间t无关,其自相关函数Rxx(nl,n2)与nl, n2的选取起点无关,而仅与n2,nI之差有关。 非平稳随机信号 大多数生物医学信号均属于非平稳随机信号,但在实 际工作中,我们往往把所要研究的非平稳随机信号视为平 稳的,这样将使问题得以大大简化
随机信号 不能通过一个确切地数学公式来描述, 不能准确地予以预测。 常见的一种平稳随机信号有:各种无线电系统及电子装置中的噪声与干扰, 生物医学信号,如心电图(ECG)、脑电图(EEG)、肌电图(EMG)、心音图等。 平稳随机信号 其均值与时间t无关,其自相关函数Rxx(n1,n2)与n1, n2的选取起点无关,而仅与n2,n1之差有关。 非平稳随机信号 大多数生物医学信号均属于非平稳随机信号,但在实 际工作中,我们往往把所要研究的非平稳随机信号视为平 稳的,这样将使问题得以大大简化

对随机信号一般只能在统计的意义上来研究 概率分布函数 P(x)=Probability (Xsx)= p(x)dx 概率密度 p(x)=dp(x)/dx 均值 ={x}=(x)d 均方值 D2=12)=Ix2 p(x)dx 方差 o2=E-)=x-u p(x)dx
对随机信号一般只能在统计的意义上来研究
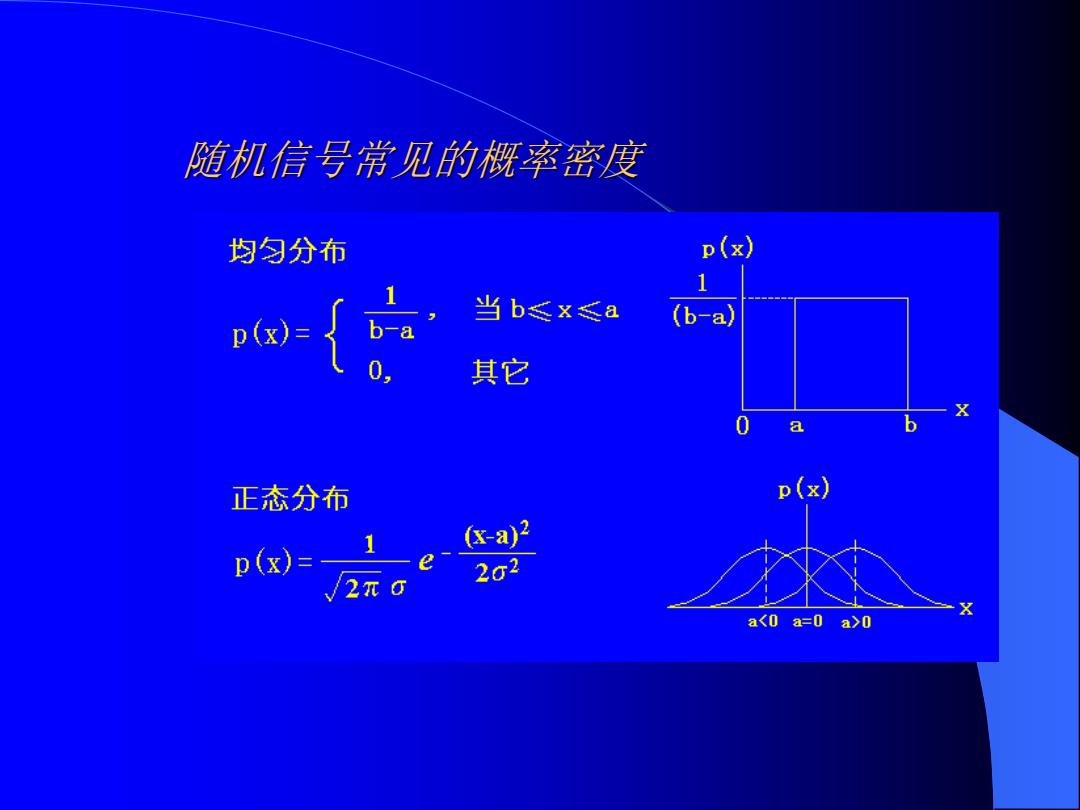
随机信号常见的概率密度 均匀分布 D(x) 当b≤x≤a (b-a) D(x) 其它 正态分布 P( -a)2 p(x)= -e /2π 202
随机信号常见的概率密度
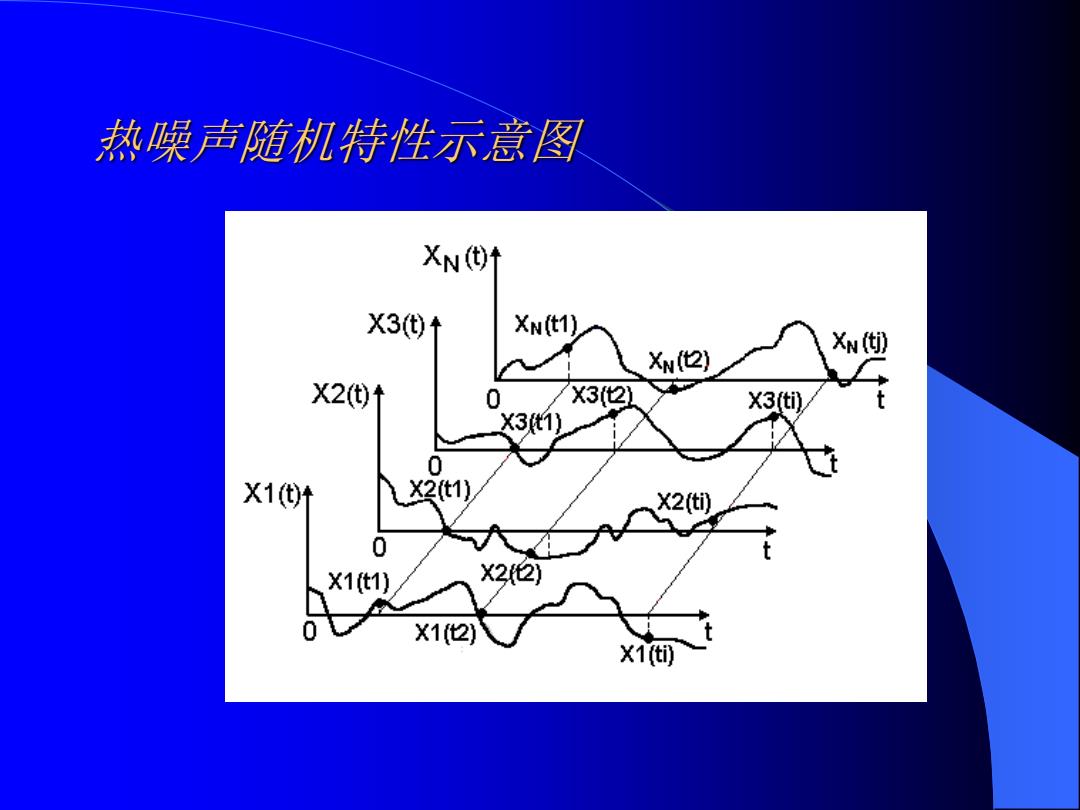
热噪声随机特性示意图 XN X3(代)↑ XN(t1) XN(t2) XN (j) X2(t) /X32】 X3(ti) 3t1) 0 X1(①t X2t1) X2(ti) 0 X1t1) X22) X12) X1t⑤
热噪声随机特性示意图

叠加平均(Average)的基本概念 ★当噪声和有用信号的频谱不相重叠时,可用数字滤 波器将二者分开;而当噪声和有用信号的频谱相重 叠时,在一定的条件下可用叠加平均的方法提高信 噪比。 ☆叠加平均法是将、个周期的信号对齐后连同噪声相 加,然后取其均值。随机的噪声在叠加的过程中会 相互抵消,而有规律的信号经叠加平均后幅度不变。 ☆适合叠加平均法的先决条件是噪声应具有随机特性, 信号则应具有重复特性,且二者互不相关
叠加平均(Average)的基本概念 当噪声和有用信号的频谱不相重叠时,可用数字滤 波器将二者分开;而当噪声和有用信号的频谱相重 叠时,在一定的条件下可用叠加平均的方法提高信 噪比。 叠加平均法是将N个周期的信号对齐后连同噪声相 加,然后取其均值。随机的噪声在叠加的过程中会 相互抵消,而有规律的信号经叠加平均后幅度不变。 适合叠加平均法的先决条件是噪声应具有随机特性, 信号则应具有重复特性,且二者互不相关

叠加平均常用方法 ●时间叠加和空间叠加 时间叠加:不同时间的同一记录点的重复信号 空间叠加:同一时间的不同记录点的相同信号 。顺叠加和逆叠加 顺叠加:叠加触发信号后的信号 逆叠加:叠加触发信号前的信号
叠加平均常用方法 ⚫ 时间叠加和空间叠加 时间叠加:不同时间的同一记录点的重复信号 空间叠加:同一时间的不同记录点的相同信号 ⚫ 顺叠加和逆叠加 顺叠加:叠加触发信号后的信号 逆叠加:叠加触发信号前的信号

叠加平均提高信噪比的统计学原理 假定一个输入波形F心由信号)和噪声N)组咸,即 F()=X()+N),并假定)在每次采样中都重复发生。我们把第次采样记作 F:)=X)+W)(i=1,2,3,···9 对N饮采样叠加平均的结果为 1x0+2 如果把噪声的方差EW2)用p2表示,则平均的方差为 即SE=pl√W, 有此可见,桌声的均方根值在N此重复后减小√W倍,由干信号在叠加平均后幅废不 变,故信噪比得到√厅倍的改善
叠加平均提高信/噪比的统计学原理
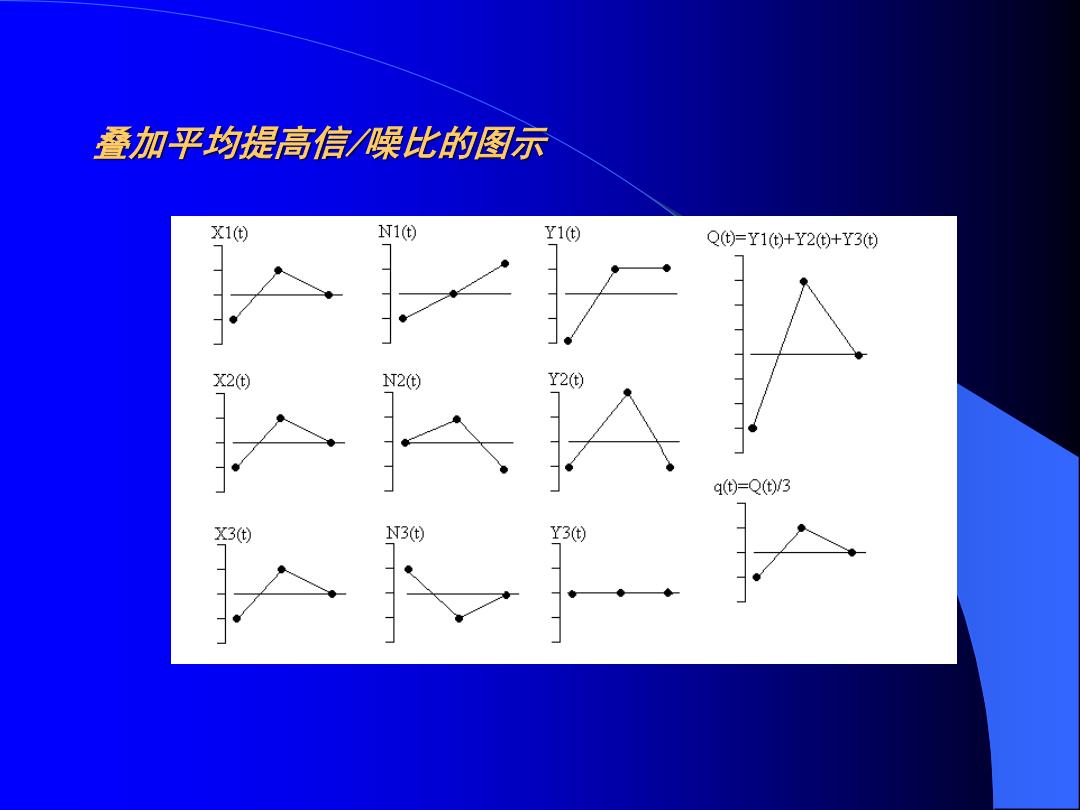
叠加平均提高信噪比的图示 N1 Y10 QtY10+Y20+Y30 X2(t 2 (t=Q(t)3
叠加平均提高信/噪比的图示