
第二章立体 2.1学习要求 (1)理解并掌握平面立体上点线的画法。 (2)理解并堂握曲面立体上点线的画法」 (3)理解并掌握常见的平面立体和常见曲面立体的基本视图,根据立体投影能够想象出立 体的空间形状。并能根据己有视图补画其他视图。 (4)理解并掌握截交线和相贯线的画法。 2.2内容简述 在学习了点线面投影的基础上,进一步研究基本几何形体的投影特点。本章的主要内容 包括平面立体上点线的画法、曲面立体上点线的画法、常见平面立体的三视图、常见曲面立 体的三视图、截交线的画法以及相贯线的画法。本章所指立体主要是平面立体(立方体、棱 柱、棱锥等)和曲面立体(圆柱、圆锥、球等)。通过本章的学习为后续的组合体部分的学 习奠定基础。 2.2.1平面立体 (1)立方体、棱柱、棱锥等的基本视图画法。 (2)立方体、棱柱、棱维表面上取点、线时的投影。在平面立体上求取点时要运用点在平 面上,则点一定在平面的一条直线上这一从属关系,并注意直线、平面的投影是否有 积聚性。平面立体上求取线的投影时, 先要在线上找特殊位置点和 要找特殊位置上的点,作好特殊位置点和一般位置点的投影后再连线。连线时应注意 可见性。 (3)平面立体被截切后的基本视图画法。 2.2.2曲面立体 (1)圆柱、圆锥、球等的基本视图画法。 (2)圆柱、圆锥、球表面上取点、线时的投影。在曲面立体上求取点的投影时要运用点在 曲面上,则点一定在曲面的一条线上这一从属关系,并注意曼、面的投影是杏有积聚 性。曲面立体上求取线的投影时,先要在线上确定特殊位置点和一般位置点,尤其要 找特殊位置上的点,这会为作图 供便利。 作好特殊位置点和一般位置点的投影后再 连线。连线时应注意可见性以及光滑连接。 (3)曲面立体被截切后的基本视图画法。 2.2.3截交线 截交线是空间立体和截平面间共有点的集合。因此截交线既在空间立体上,也在截平面 上。平面立体与截平面的截交线形状是封闭多边形。曲面立体与截平面的截交线形状与曲面 立体的形状以及截平面的位置有关。截平面与圆柱的截交线包括矩形、圆和椭圆三种形状。 载平面与圆锥的截交线包括三角形、圆、椭圆、物线和双曲线五种形状。截平面与球的载 交线形状为圆,但是投影可以为直线、椭圆或圆。 绘制截交线的基本作图步骤如下: 多
第二章 立体 2.1 学习要求 (1)理解并掌握平面立体上点线的画法。 (2)理解并掌握曲面立体上点线的画法。 (3)理解并掌握常见的平面立体和常见曲面立体的基本视图,根据立体投影能够想象出立 体的空间形状。并能根据已有视图补画其他视图。 (4)理解并掌握截交线和相贯线的画法。 2.2 内容简述 在学习了点线面投影的基础上,进一步研究基本几何形体的投影特点。本章的主要内容 包括平面立体上点线的画法、曲面立体上点线的画法、常见平面立体的三视图、常见曲面立 体的三视图、截交线的画法以及相贯线的画法。本章所指立体主要是平面立体(立方体、棱 柱、棱锥等)和曲面立体(圆柱、圆锥、球等)。通过本章的学习为后续的组合体部分的学 习奠定基础。 2.2.1 平面立体 (1)立方体、棱柱、棱锥等的基本视图画法。 (2)立方体、棱柱、棱锥表面上取点、线时的投影。在平面立体上求取点时要运用点在平 面上,则点一定在平面的一条直线上这一从属关系,并注意直线、平面的投影是否有 积聚性。平面立体上求取线的投影时,先要在线上找特殊位置点和一般位置点,尤其 要找特殊位置上的点,作好特殊位置点和一般位置点的投影后再连线。连线时应注意 可见性。 (3)平面立体被截切后的基本视图画法。 2.2.2 曲面立体 (1)圆柱、圆锥、球等的基本视图画法。 (2)圆柱、圆锥、球表面上取点、线时的投影。在曲面立体上求取点的投影时要运用点在 曲面上,则点一定在曲面的一条线上这一从属关系,并注意线、面的投影是否有积聚 性。曲面立体上求取线的投影时,先要在线上确定特殊位置点和一般位置点,尤其要 找特殊位置上的点,这会为作图提供便利。作好特殊位置点和一般位置点的投影后再 连线。连线时应注意可见性以及光滑连接。 (3)曲面立体被截切后的基本视图画法。 2.2.3 截交线 截交线是空间立体和截平面间共有点的集合。因此截交线既在空间立体上,也在截平面 上。平面立体与截平面的截交线形状是封闭多边形。曲面立体与截平面的截交线形状与曲面 立体的形状以及截平面的位置有关。截平面与圆柱的截交线包括矩形、圆和椭圆三种形状。 截平面与圆锥的截交线包括三角形、圆、椭圆、抛物线和双曲线五种形状。截平面与球的截 交线形状为圆,但是投影可以为直线、椭圆或圆。 绘制截交线的基本作图步骤如下: 19

(1)首先进行形体分析,通过立体的空间形状以及截平面的截切位置分析截交线的形状。 (2)在已知视图中找到截交线的已有投影。 任上知投影上取一些点,包,括特殊位置点和一般位置点。特殊位置点包括最高点、最 低点 最左点 、最右点、最前点、最后点以及转向素线上的点。 殊位置点以外的点。 (4)先求特殊位置点的投影,后求一般位置点的投影。 (5)判别可见性,将点的投影光滑连线,擦去多余的线,不可见部分用虚线表示。 2.2.4相贯线 由立体相交而形成的表面交线称为相贯线。因此相贸线在两个立体表面上。相贯线的形 状与两个回转体的立体形状、立体大小以及相对位置有关。一般情况下相贯线是封闭的空间 曲线,特殊桔况下也可以是平面曲线成有线。 相贯线的基本作图步骤如 (1)首先进行形体分析,通过相交立体的空间形状分析相贯线的形状。 (2)在已知视图中找到相贯线的已有投影。 (3)在已知投影上取一些点,包括特殊位置点和一般位置点。特殊位置点包括最高点、最 低点、最左点、最右点、最前点、最后点以及转向素线上的点。一般位置点是指除特 殊位置占以外的占 (4)用立体表面取点法求点的投影,先求特殊位置点的投影,后求一般位置点的投影 (5)判别可见性,将点的投影光滑连线,擦去多余的线,不可见部分用虚线表示。 在绘制相贯线时,应该注意以下几点: (1)特殊点和一般位置点需要选好。 (2)一般点的数量视点之间的空格大小而定。 (3)连线时应注意可见性。 2.3本章知识点 (1)阅读平面立体视图,想象出空间立体形状以及补画其他视图 (2)平面立体表面上点和线的投影。 (3)阅读曲面立体视图,想象出空间立体形状以及补画其他视图 (4)曲面立体表面上点和线的投影。 (5)截交线画法,应注意截切位置不同以及立体空间形状不同对截交线形状的影响。 (6)相贯线画法,应注意不同空间立体以及空间立体之间的相对位置关系对相贯线形状的 影响。 2.4思考题 (1)两个圆柱相交时,两者直径大小变化对相贯线形状的影响? (2)平行于圆柱轴线的平面对圆柱进行截切时,截交线是什么形状? (3)垂直于圆柱轴线的平面对圆柱进行截切时,截交线是什么形状? (4)两个直径相等,轴线相交的圆柱相贯时,相贯线是什么形状? 2.5例题与习题解答 2.5.1例题
(1)首先进行形体分析,通过立体的空间形状以及截平面的截切位置分析截交线的形状。 (2)在已知视图中找到截交线的已有投影。 (3)在已知投影上取一些点,包括特殊位置点和一般位置点。特殊位置点包括最高点、最 低点、最左点、最右点、最前点、最后点以及转向素线上的点。一般位置点是指除特 殊位置点以外的点。 (4)先求特殊位置点的投影,后求一般位置点的投影。 (5)判别可见性,将点的投影光滑连线,擦去多余的线,不可见部分用虚线表示。 2.2.4 相贯线 由立体相交而形成的表面交线称为相贯线。因此相贯线在两个立体表面上。相贯线的形 状与两个回转体的立体形状、立体大小以及相对位置有关。一般情况下相贯线是封闭的空间 曲线,特殊情况下也可以是平面曲线或直线。 相贯线的基本作图步骤如下: (1)首先进行形体分析,通过相交立体的空间形状分析相贯线的形状。 (2)在已知视图中找到相贯线的已有投影。 (3)在已知投影上取一些点,包括特殊位置点和一般位置点。特殊位置点包括最高点、最 低点、最左点、最右点、最前点、最后点以及转向素线上的点。一般位置点是指除特 殊位置点以外的点。 (4)用立体表面取点法求点的投影,先求特殊位置点的投影,后求一般位置点的投影。 (5)判别可见性,将点的投影光滑连线,擦去多余的线,不可见部分用虚线表示。 在绘制相贯线时,应该注意以下几点: (1)特殊点和一般位置点需要选好。 (2)一般点的数量视点之间的空格大小而定。 (3)连线时应注意可见性。 2.3 本章知识点 (1)阅读平面立体视图,想象出空间立体形状以及补画其他视图。 (2)平面立体表面上点和线的投影。 (3)阅读曲面立体视图,想象出空间立体形状以及补画其他视图。 (4)曲面立体表面上点和线的投影。 (5)截交线画法,应注意截切位置不同以及立体空间形状不同对截交线形状的影响。 (6)相贯线画法,应注意不同空间立体以及空间立体之间的相对位置关系对相贯线形状的 影响。 2.4 思考题 (1)两个圆柱相交时,两者直径大小变化对相贯线形状的影响? (2)平行于圆柱轴线的平面对圆柱进行截切时,截交线是什么形状? (3)垂直于圆柱轴线的平面对圆柱进行截切时,截交线是什么形状? (4)两个直径相等,轴线相交的圆柱相贯时,相贯线是什么形状? 2.5 例题与习题解答 2.5.1 例题 20
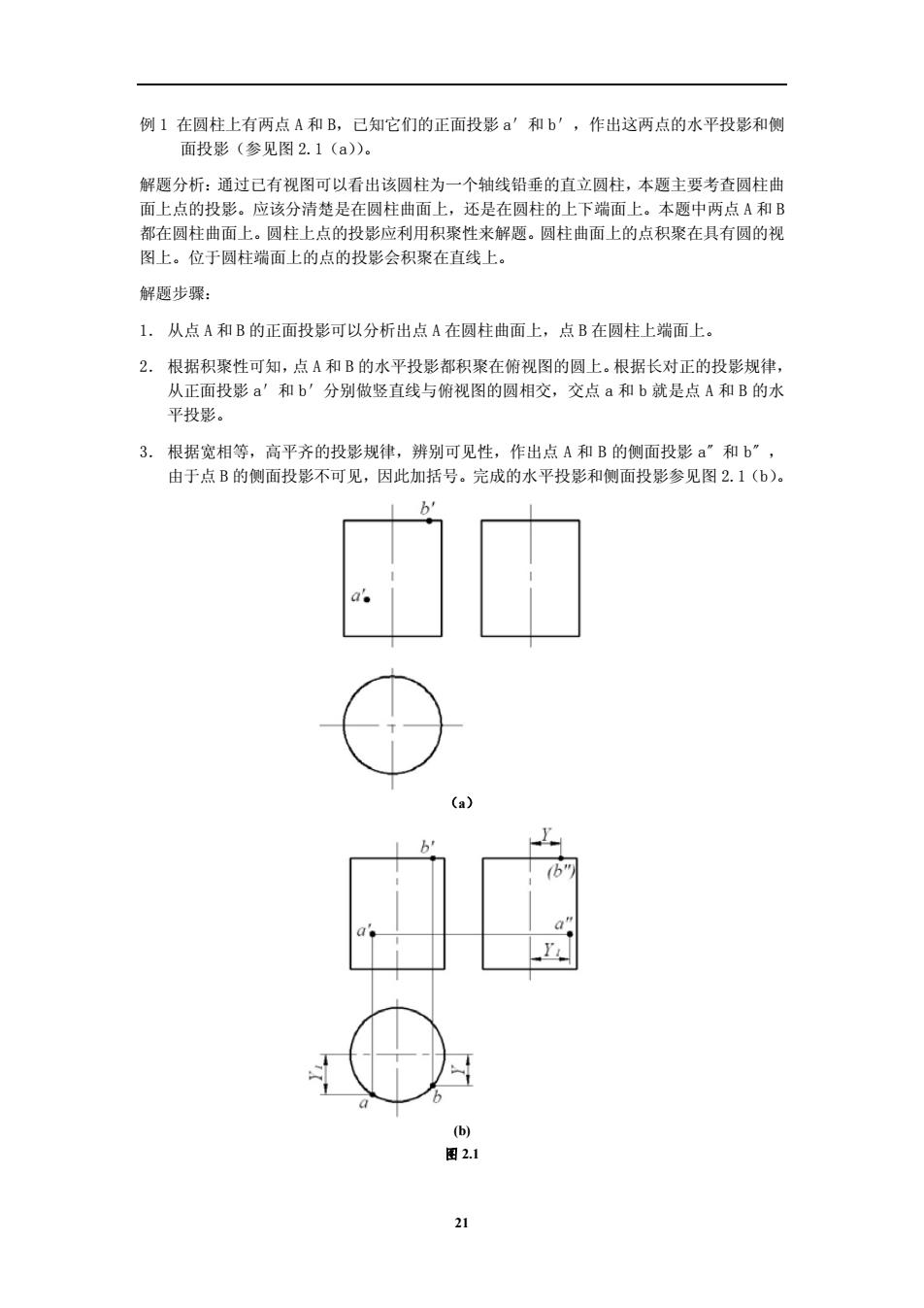
例1在圆柱上有两点A和B,己知它们的正面投影a'和b',作出这两点的水平投影和侧 面投影(参见图2.1(a)。 解题分析:通过已有视图可以看出该圆柱为一个轴线铅垂的直立圆柱,本题主要考查圆柱曲 面上点的投影。应该分清楚是在圆柱曲面上,还是在圆柱的上下端面上。本题中两点A和B 都在圆柱曲面上。圆柱上点的投影应利用积聚性来解题。圆柱曲面上的点积聚在具有圆的视 图上。位于圆柱面上的点的投影会积聚在直线上。 解题步骤: 1.从点A和B的正面投影可以分析出点A在圆柱曲面上,点B在圆柱上端面上。 2.根据积聚性可知,点A和B的水平投影都积聚在俯视图的圆上。根据长对正的投影规律, 从正面投影a'和b'分别做竖直线与俯视图的圆相交,交点a和b就是点A和B的水 平投影。 3.根据宽相等,高平齐的投影规律,辨别可见性,作出点A和B的侧面投影a”和b” 由于点B的侧面投影不可见,因此加括号,完成的水平投影和侧面投影参见图2.1(b)。 图2.1
例 1 在圆柱上有两点 A 和 B,已知它们的正面投影 a′和 b′,作出这两点的水平投影和侧 面投影(参见图 2.1(a))。 解题分析:通过已有视图可以看出该圆柱为一个轴线铅垂的直立圆柱,本题主要考查圆柱曲 面上点的投影。应该分清楚是在圆柱曲面上,还是在圆柱的上下端面上。本题中两点 A 和 B 都在圆柱曲面上。圆柱上点的投影应利用积聚性来解题。圆柱曲面上的点积聚在具有圆的视 图上。位于圆柱端面上的点的投影会积聚在直线上。 解题步骤: 1. 从点 A 和 B 的正面投影可以分析出点 A 在圆柱曲面上,点 B 在圆柱上端面上。 2. 根据积聚性可知,点 A 和 B 的水平投影都积聚在俯视图的圆上。根据长对正的投影规律, 从正面投影 a′和 b′分别做竖直线与俯视图的圆相交,交点 a 和 b 就是点 A 和 B 的水 平投影。 3. 根据宽相等,高平齐的投影规律,辨别可见性,作出点 A 和 B 的侧面投影 a〞和 b〞, 由于点 B 的侧面投影不可见,因此加括号。完成的水平投影和侧面投影参见图 2.1(b)。 (a) (b) 图 2.1 21

例2在圆锥上有点A,已知它的正面投影a',作出该点的水平投影和侧面投影(参见图2.2 (a))。 解分析:通过已有视图可以看出目中为销线铅垂的圆维、本主要考在圆维曲面上点的 投影。求取圆锥曲面上点的投影一般有两种方法求解,素线法和辅助圆法。 解愿步骤: 素线法作点的投影: 1.从点A的正面投影可以分析出点A在圆锥曲面上。 2.过圆锥项点和点A的正面投影a'作一条直线,该直线与圆锥底面的正面投影交于点B, 从而得到点B的正面投影b'。 3.根据长对正的投影规律,从正面投影b'做竖直线与俯视图的圆相交,交点b就是点B 4.根据宽相等,高平齐的投影规律,辨别可见性,作出点A的侧面投影a”。参见图22 (b). 辅助圆法作点的投影 1.从点A的正面投影可以分析出点A在圆锥曲面上。 2.过点A做一个水平辅助圆,该水平辅助圆的正面投影积聚为一条直线,点A的正面投影 a'必然在这条直线上。该水平辅助圆的水平投影为圆,点A的水平投影a必然在这个 圆上。 3.过点A的正面投影a'作一条直线,与圆锥的主视图相交,得到该水平辅助圆的半径r。 4.在俯视图中,以圆锥俯视图的圆心为圆心,以r为半径作出水平辅助圆的水平投影。根 据长对正的投影规律,从点A的正面投影a'作竖直线与俯视图的水平辅助圆投影相交, 交点为点A的水平投影a。 5. 根据宽相等,高平齐的投影规律,辨别可见性,作出点A的侧面投影a”。参见图2.2 (c)
例 2 在圆锥上有点 A,已知它的正面投影 a′,作出该点的水平投影和侧面投影(参见图 2.2 (a))。 解题分析:通过已有视图可以看出题目中为轴线铅垂的圆锥。本题主要考查圆锥曲面上点的 投影。求取圆锥曲面上点的投影一般有两种方法求解,素线法和辅助圆法。 解题步骤: 素线法作点的投影: 1. 从点 A 的正面投影可以分析出点 A 在圆锥曲面上。 2. 过圆锥顶点和点 A 的正面投影 a′作一条直线,该直线与圆锥底面的正面投影交于点 B, 从而得到点 B 的正面投影 b′。 3. 根据长对正的投影规律,从正面投影 b′做竖直线与俯视图的圆相交,交点 b 就是点 B 的水平投影。连接俯视图圆心和 b 得到一条直线,点 A 的水平投影 a 必然在这条直线上, 从正面投影 a′做竖直线与这条直线相交,得到点 A 的水平投影 a。 4. 根据宽相等,高平齐的投影规律,辨别可见性,作出点 A 的侧面投影 a〞。参见图 2.2 (b)。 辅助圆法作点的投影: 1. 从点 A 的正面投影可以分析出点 A 在圆锥曲面上。 2. 过点 A 做一个水平辅助圆,该水平辅助圆的正面投影积聚为一条直线,点 A 的正面投影 a′必然在这条直线上。该水平辅助圆的水平投影为圆,点 A 的水平投影 a 必然在这个 圆上。 3. 过点 A 的正面投影 a′作一条直线,与圆锥的主视图相交,得到该水平辅助圆的半径 r。 4. 在俯视图中,以圆锥俯视图的圆心为圆心,以 r 为半径作出水平辅助圆的水平投影。根 据长对正的投影规律,从点 A 的正面投影 a′作竖直线与俯视图的水平辅助圆投影相交, 交点为点 A 的水平投影 a。 5. 根据宽相等,高平齐的投影规律,辨别可见性,作出点 A 的侧面投影 a〞。参见图 2.2 (c)。 (a) (b) 22
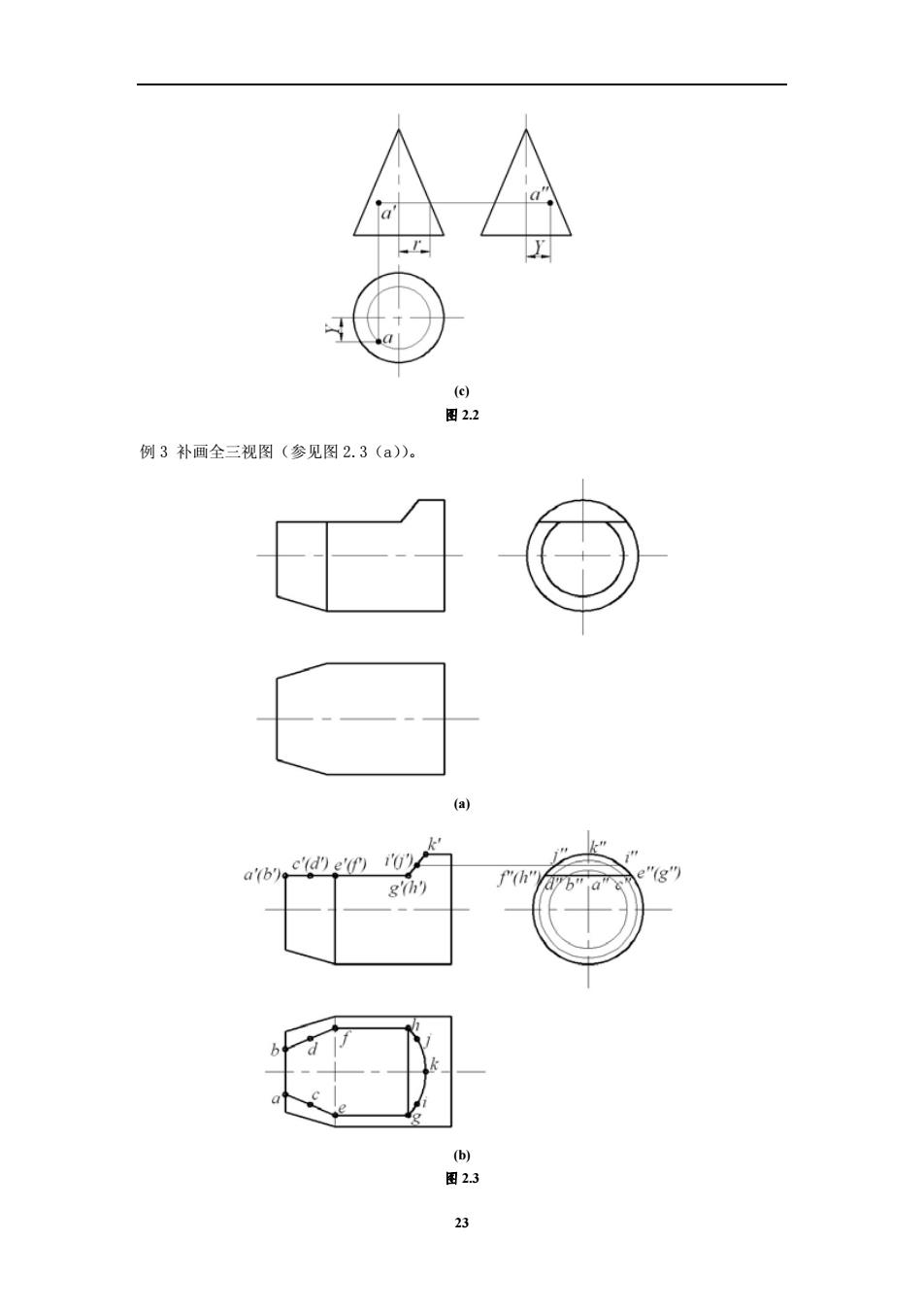
图2.2 例3补画全三视图(参见图2.3(a)。 a'b c'd)e'(f)i) h 图23
(c) 图 2.2 例 3 补画全三视图(参见图 2.3(a))。 (a) (b) 图 2.3 23

解题分析:通过己有视图分析可知该形体为轴线侧垂的回转体,本题主要考查回转体的投影 作图,截平面分别与圆锥台和圆柱截交。由已有视图可知由圆锥台和圆柱组合成的回转体被 个水平面和一个正垂面截切。圆锥台和圆柱同轴线。截交线分为三部分 部分是水平面 与圆锥台的截交线 一部分是水平面与圆柱的截交线,还有 部分是正垂面与圆柱的交线 水平面与圆锥台的截交线的正面投影积聚在主视图的直线上。水平面与圆柱的截交线的正面 投影也积聚在主视图的直线上。正垂面与圆柱的截交线的侧面投影积聚在左视图的圆上。本 题目需要补画的是水平面与圆锥台的截交线的水平投影,水平面与圆柱的截交线的水平投 影,正垂面与圆柱的截交线的水平投影。 解题步骤 1.先作出水平面与圆雏台的截交线,由于该截交线在主视图上的投影积聚为一条直线,因 此在该直线上选取六个点A、B、C、D、E、F的正面投影a'、b'、c'、d'、e'、f 。A和B两点在左端面上,利用辅助圆法作出它们的侧面投影a”和b”。根据A和B 两点的正面投影a'、b'和侧面投影a”和b” ,作出水平投影a和b。同样利用辅助圆 法作出C和D两点的侧面投影c 和d°,根据C和D两点的正面投影 、d'和侧面 投影c“和d”,作出它们的水平投影c和d。E和F两点是水平面与圆锥台底面交线上 的两个端点,这两点的侧面投影e”和f”积聚在左视图的圆上,根据E和F两点的正面 投影e'、f'以及侧面投影e”、f”求出点E和点F的水平投影e和f。在俯视图中顺 序光滑连接B、D、F三点的水平投影b、d、f以及A、C、E三点的水平投影a、c、e, 得到水平面与圆锥台的截交线的水平投影。 2.水平面与圆柱的截交线为矩形,根据投影关系作出水平面与圆柱的截交线。G和H两点 是水平面与圆柱交线上的两个点,这两点的侧面投影g”和h”积聚在左视图的圆上,根 据G和H两点的正面投影g'、h'以及侧面投影g”、h”求出点G和点H的水平投影 和h。连接fh、hg以及eg 3.正垂面与圆柱的截交线为椭圆的一部分,椭圆在主视图上的投影积聚为一直线,在该直 线上选取G、H、I、丁、K五点的正面投影g'、h'、i'、'、k'。G和H两点的水平 投影在上一步中己经作出,点K是椭圆的最高点,它的水平投影k利用投影关系直接作 卧动致经的食发数厚华在高幸:用 作 点I和点J的水平投影i和j。顺序光滑连接G、I、K、、K五点的水平投影 g、、k,j、h得到正垂面与圆柱的被交线的水平投影。 4.检查是否有被遮挡的结构,遮挡部分用虚线表示,参见图2.3(b)。 例4根据主视图和俯视图,补画左视图。(参见图2.4(a)。 解题分析:该形体为在立方体基础上进行挖切。从主视图和俯视图可以看出左边被正垂面截 切。正垂面与立方体的截交线形状为矩形。然后在立方体上部挖切了一个槽,这个槽主要形 状可以从俯视图中看出。本题主要考查立体的投影作图以及截交线的画法。 解题步骤: 1.绘制被正垂面截切后的立方体的侧面投影。 2.绘制挖切槽后的侧面投影,参见图2.4(b)。 2
解题分析:通过已有视图分析可知该形体为轴线侧垂的回转体,本题主要考查回转体的投影 作图,截平面分别与圆锥台和圆柱截交。由已有视图可知由圆锥台和圆柱组合成的回转体被 一个水平面和一个正垂面截切。圆锥台和圆柱同轴线。截交线分为三部分,一部分是水平面 与圆锥台的截交线,一部分是水平面与圆柱的截交线,还有一部分是正垂面与圆柱的截交线。 水平面与圆锥台的截交线的正面投影积聚在主视图的直线上。水平面与圆柱的截交线的正面 投影也积聚在主视图的直线上。正垂面与圆柱的截交线的侧面投影积聚在左视图的圆上。本 题目需要补画的是水平面与圆锥台的截交线的水平投影,水平面与圆柱的截交线的水平投 影,正垂面与圆柱的截交线的水平投影。 解题步骤: 1. 先作出水平面与圆锥台的截交线,由于该截交线在主视图上的投影积聚为一条直线,因 此在该直线上选取六个点 A、B、C、D、E、F 的正面投影 a′、b′、c′、d′、e′、f ′。A 和 B 两点在左端面上,利用辅助圆法作出它们的侧面投影 a〞和 b〞。根据 A 和 B 两点的正面投影 a′、b′和侧面投影 a〞和 b〞,作出水平投影 a 和 b。同样利用辅助圆 法作出 C 和 D 两点的侧面投影 c〞和 d〞, 根据 C 和 D 两点的正面投影 c′、d′和侧面 投影 c〞和 d〞,作出它们的水平投影 c 和 d。E 和 F 两点是水平面与圆锥台底面交线上 的两个端点,这两点的侧面投影 e〞和 f〞积聚在左视图的圆上,根据 E 和 F 两点的正面 投影 e′、f′以及侧面投影 e〞、f〞求出点 E 和点 F 的水平投影 e 和 f。在俯视图中顺 序光滑连接 B、D、F 三点的水平投影 b、d、f 以及 A、C、E 三点的水平投影 a、c、e, 得到水平面与圆锥台的截交线的水平投影。 2. 水平面与圆柱的截交线为矩形,根据投影关系作出水平面与圆柱的截交线。G 和 H 两点 是水平面与圆柱交线上的两个点,这两点的侧面投影 g〞和 h〞积聚在左视图的圆上,根 据 G 和 H 两点的正面投影 g′、h′以及侧面投影 g〞、h〞求出点 G 和点 H 的水平投影 g 和 h。连接 fh、hg 以及 eg。 3. 正垂面与圆柱的截交线为椭圆的一部分,椭圆在主视图上的投影积聚为一直线,在该直 线上选取 G、H、I、J、K 五点的正面投影 g′、h′、i′、j′、k′。G 和 H 两点的水平 投影在上一步中已经作出,点 K 是椭圆的最高点,它的水平投影 k 利用投影关系直接作 出。I 和 J 两点是椭圆上的一般点,根据积聚性,它们的侧面投影在左视图的圆上,作 出它们的侧面投影 i〞和 j〞。根据点 I 和点 J 的正面投影 i′、j′以及侧面投影 i〞、 j〞,作出点 I 和点 J 的水平投影 i 和 j。顺序光滑连接 G、I、K、J、K 五点的水平投影 g、i、k、j、h 得到正垂面与圆柱的截交线的水平投影。 4. 检查是否有被遮挡的结构,遮挡部分用虚线表示,参见图 2.3(b)。 例 4 根据主视图和俯视图,补画左视图。(参见图 2.4(a))。 解题分析:该形体为在立方体基础上进行挖切。从主视图和俯视图可以看出左边被正垂面截 切。正垂面与立方体的截交线形状为矩形。然后在立方体上部挖切了一个槽,这个槽主要形 状可以从俯视图中看出。本题主要考查立体的投影作图以及截交线的画法。 解题步骤: 1. 绘制被正垂面截切后的立方体的侧面投影。 2. 绘制挖切槽后的侧面投影,参见图 2.4(b)。 24
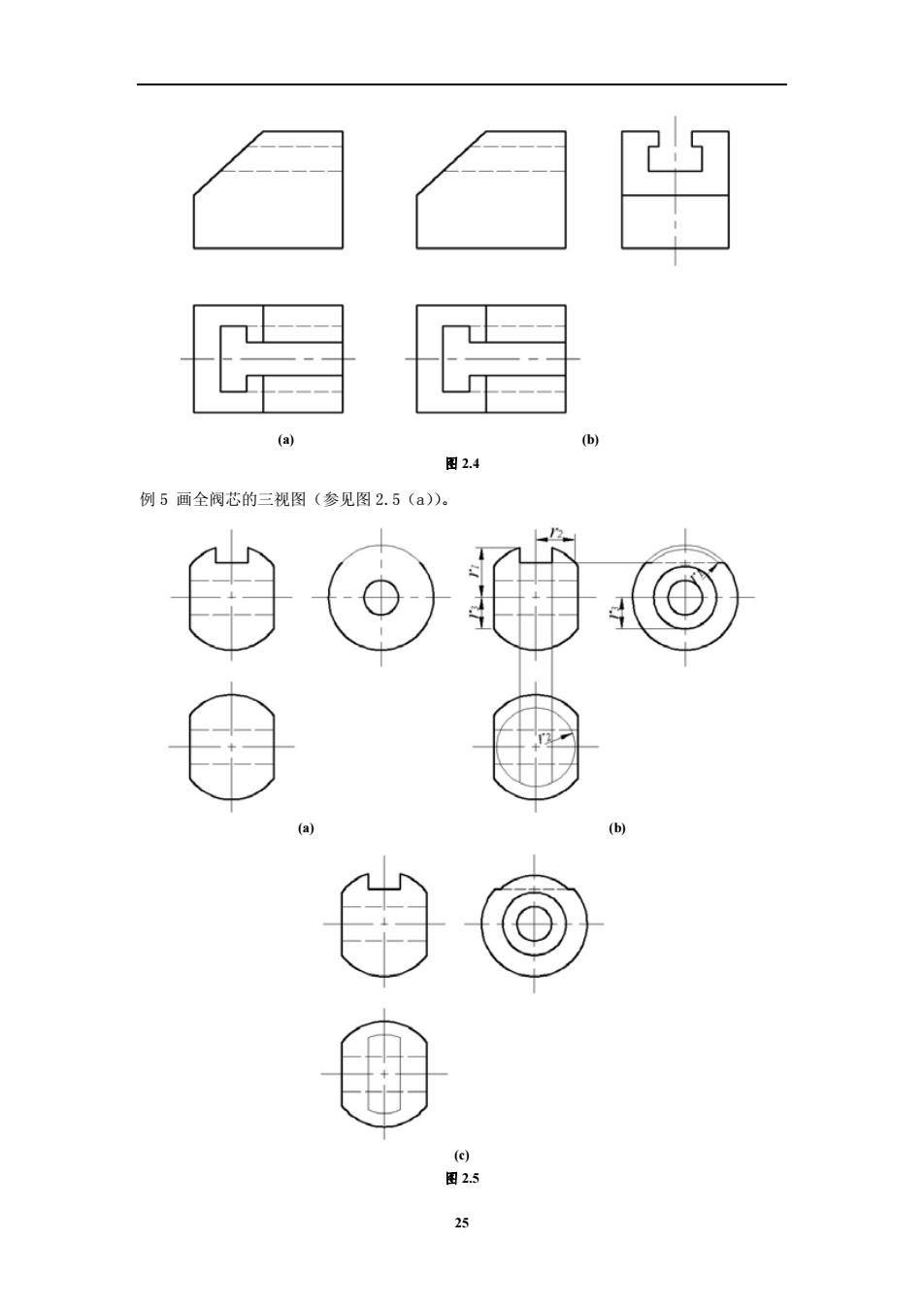
(a) 图2.4 例5画全阀芯的三视图(参见图2.5(a)。 D D 图25
(a) (b) 图 2.4 例 5 画全阀芯的三视图(参见图 2.5(a))。 (a) (b) (c) 图 2.5 25
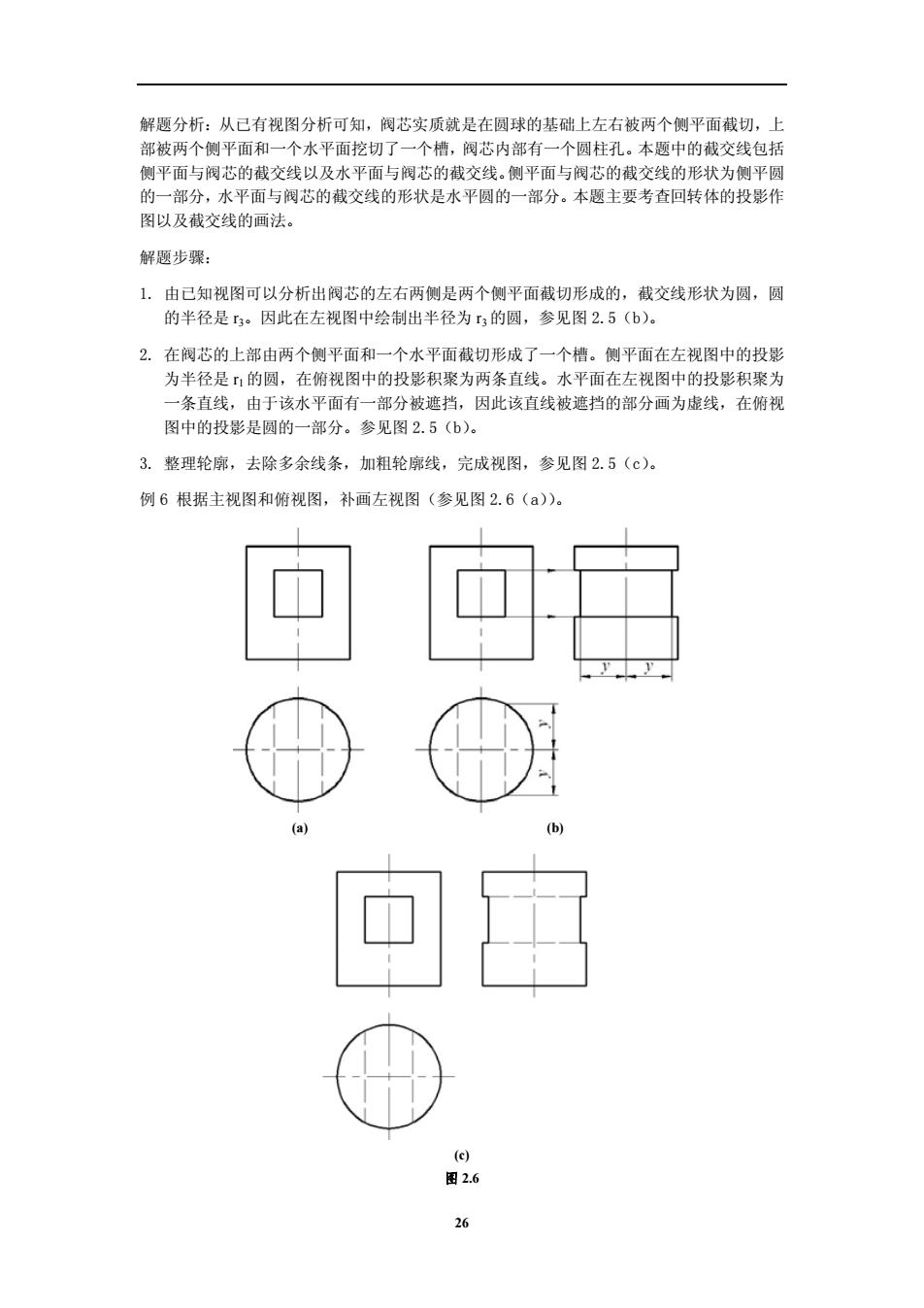
解题分析:从己有视图分析可知,阀芯实质就是在圆球的基础上左右被两个侧平面截切,上 部被两个侧平面和一个水平面挖切了一个抽,阀芯内部有一个圆柱孔。本颗中的截交线包括 侧平面与阀芯的截交线以及水平面与阀芯的截交线。侧平面与阀芯的截交线的形状为侧平圆 水平面与阀芯的截交线的形状是水平圆的一部分。本题主要考查回转体的投影作 解题步骤: 1.由已知视图可以分析出阀芯的左右两侧是两个侧平面截切形成的,截交线形状为圆,圆 的半径是3。因此在左视图中绘制出半径为3的圆, 参见图2.5(b) 2.在阀芯的上部由两个侧平面和一个水平面截切形成了一个槽。侧平面在左视图中的投影 为半径是的圆,在俯视图中的投影积聚为两条直线。水平面在左视图中的投影积聚为 一条直线,由于该水平面有一部分被遮挡,因此该直线被遮挡的部分画为虚线,在俯视 图中的投影是圆的一部分。参见图25(b)。 3.整理轮廓,去除多余线条,加粗轮廓线,完成视图,参见图2.5(c)。 例6根据主视图和俯视图,补画左视图(参见图2.6())
解题分析:从已有视图分析可知,阀芯实质就是在圆球的基础上左右被两个侧平面截切,上 部被两个侧平面和一个水平面挖切了一个槽,阀芯内部有一个圆柱孔。本题中的截交线包括 侧平面与阀芯的截交线以及水平面与阀芯的截交线。侧平面与阀芯的截交线的形状为侧平圆 的一部分,水平面与阀芯的截交线的形状是水平圆的一部分。本题主要考查回转体的投影作 图以及截交线的画法。 解题步骤: 1. 由已知视图可以分析出阀芯的左右两侧是两个侧平面截切形成的,截交线形状为圆,圆 的半径是 r3。因此在左视图中绘制出半径为 r3的圆,参见图 2.5(b)。 2. 在阀芯的上部由两个侧平面和一个水平面截切形成了一个槽。侧平面在左视图中的投影 为半径是 r1的圆,在俯视图中的投影积聚为两条直线。水平面在左视图中的投影积聚为 一条直线,由于该水平面有一部分被遮挡,因此该直线被遮挡的部分画为虚线,在俯视 图中的投影是圆的一部分。参见图 2.5(b)。 3. 整理轮廓,去除多余线条,加粗轮廓线,完成视图,参见图 2.5(c)。 例 6 根据主视图和俯视图,补画左视图(参见图 2.6(a))。 (a) (b) (c) 图 2.6 26

解题分析:由主视图和俯视图可以分析出该空间立体为轴线铅垂的直立圆柱,在圆柱的中间 部分从前到后有一个方槽,这个方槽被两个水平面和两个侧平面截切而成。两个水平面与圆 柱的轴线垂直,交线为水平圆 两个侧平面与圆柱的轴线平行,截交线为矩形。本题主要考 查回转体的投影作图以及截交线的画法。 解顾步骤: 1.根据“长对正,宽相等,高平齐”的投影规律画出圆柱的左视图。 2。根据“宽相等”的投影规律作出方槽的侧平面与圆柱外表面交线的侧面投影。方槽的侧 平面在俯视图中的投影积聚为一条直线,参见图2.6(b)。 3.根据“高平齐”的投影规律作出水平面的侧面投影,由于水平面部分不可见,因此不可 见的部分画为虚线。水平面在俯视图的投影积聚在圆上。 4.去掉辅助线,加粗左视图轮廓,补画好的左视图参见图2.6(c)。 例7根据主视图和俯视图,补画左视图(参见图2.7(a)。 解题分析:通过主视图和俯视图可以分析出,空间立体为轴线铅垂的直立圆柱,在直立圆柱 内部有一个同轴线的直立圆柱孔。在直立圆柱中间部分具有一个轴线与直立圆柱轴线垂直的 圆柱孔,这个圆柱孔从直立圆柱的前部开始一直打通到后部。这个圆柱孔与直立圆柱和直立 圆柱孔形成的相贯线包括两部分 分是直径不同的直立圆柱外表面与圆柱孔形成的相贯 线:另一部分是直径相等的两个圆柱孔形成的相贯线。本题主要考查回转体的投影作图以及 相贯线的画法。 解题步骤: 1.绘制圆柱在左视图中的投影 2.绘制圆柱孔的侧面投影,尤其应注意圆柱与圆柱孔之间的相贷线,以及圆柱孔与圆柱孔 之间的相贯线,由于圆柱孔与圆柱孔之间的相贯线在内部,不可见,因此画为虚线。补 画好的左视图参见图2.7(b)。 图2.1
解题分析:由主视图和俯视图可以分析出该空间立体为轴线铅垂的直立圆柱,在圆柱的中间 部分从前到后有一个方槽,这个方槽被两个水平面和两个侧平面截切而成。两个水平面与圆 柱的轴线垂直,交线为水平圆。两个侧平面与圆柱的轴线平行,截交线为矩形。本题主要考 查回转体的投影作图以及截交线的画法。 解题步骤: 1. 根据“长对正,宽相等,高平齐”的投影规律画出圆柱的左视图。 2. 根据“宽相等”的投影规律作出方槽的侧平面与圆柱外表面交线的侧面投影。方槽的侧 平面在俯视图中的投影积聚为一条直线,参见图 2.6(b)。 3. 根据“高平齐”的投影规律作出水平面的侧面投影,由于水平面部分不可见,因此不可 见的部分画为虚线。水平面在俯视图的投影积聚在圆上。 4. 去掉辅助线,加粗左视图轮廓,补画好的左视图参见图 2.6(c)。 例 7 根据主视图和俯视图,补画左视图(参见图 2.7(a))。 解题分析:通过主视图和俯视图可以分析出,空间立体为轴线铅垂的直立圆柱,在直立圆柱 内部有一个同轴线的直立圆柱孔。在直立圆柱中间部分具有一个轴线与直立圆柱轴线垂直的 圆柱孔,这个圆柱孔从直立圆柱的前部开始一直打通到后部。这个圆柱孔与直立圆柱和直立 圆柱孔形成的相贯线包括两部分,一部分是直径不同的直立圆柱外表面与圆柱孔形成的相贯 线;另一部分是直径相等的两个圆柱孔形成的相贯线。本题主要考查回转体的投影作图以及 相贯线的画法。 解题步骤: 1. 绘制圆柱在左视图中的投影。 2. 绘制圆柱孔的侧面投影,尤其应注意圆柱与圆柱孔之间的相贯线,以及圆柱孔与圆柱孔 之间的相贯线,由于圆柱孔与圆柱孔之间的相贯线在内部,不可见,因此画为虚线。补 画好的左视图参见图 2.7(b)。 (a) (b) 图 2.7 27

2.5.2习题及答案 习题1作出六棱柱的左视图,根据六棱柱上点A和点B的正面投影,求作这两点的水平投影 和侧面投影(参见图2.8(a》 解题分析:六棱柱包括上下两个底面以及其他六个面。两个底面为正平面,其他六个面为四 个铅垂面和两个正平面。从题中可以看出点A和点B都在铅垂面上。根据点A和点B的正面 投影可以看出点B被遮挡,因此点B在六棱柱后侧的面上。点A可见,因此点A在六棱柱前 侧的面上。本题需要利用积聚性来解恩。本主要考查立体的投影作图以及面上取点的投影 画法。 解题步骤: 1.根据积聚性,可以作出点A的水平投影a,由于点B的正面投影不可见,因此点B在六 棱柱后侧的铅垂面上。根据积聚性作出点B的水平投影b。 2.根据点A的水平投影a和正面投影a',按照“长对正、宽相等、高平齐”的投影规律 作出点A的侧面投影a”.参见图2.8(b)。 3.根据点B的水平投影b和正面投影b',按照投影规律作出它的侧面投影b”,由于点B 的侧面投影不可见,因此点B的侧面投影b加括号,参见图2.8(b)。 图2.8 习题2己知圆锥台曲面上的线ABC的正面投影,求作其侧面投影和水平投影(参见图2.9 解题分析:从图中可以看出该形体为轴线正垂线的半圆锥台。本题主要考查回转体的投影作 图以及圆锥台表面上线的投影,可以采用铺助圆法来解题。在线上应该选取一些特殊位置点 和一般位置点。本题中线上的特殊位置点包括最左点(最下点)A、最右点C以及最上点B。 此外需要在点A和点B之间以及点B和点C之间选取一般位置点。将这些点在俯视图和左视 图中的投影确定好之后,光滑连线即得到线ABC的侧面投影和水平投影。 解题步骤: 1.由于A、B、C三点是特殊位置点,分别是最左点、最上点和最右点。利用辅助圆法先作 出这三点的水平投影a、b、c和侧面投影a”、b”、c”。以点A为例,过点A作正平
2.5.2 习题及答案 习题 1 作出六棱柱的左视图,根据六棱柱上点 A 和点 B 的正面投影,求作这两点的水平投影 和侧面投影(参见图 2.8(a))。 解题分析:六棱柱包括上下两个底面以及其他六个面。两个底面为正平面,其他六个面为四 个铅垂面和两个正平面。从题中可以看出点 A 和点 B 都在铅垂面上。根据点 A 和点 B 的正面 投影可以看出点 B 被遮挡,因此点 B 在六棱柱后侧的面上。点 A 可见,因此点 A 在六棱柱前 侧的面上。本题需要利用积聚性来解题。本题主要考查立体的投影作图以及面上取点的投影 画法。 解题步骤: 1.根据积聚性,可以作出点 A 的水平投影 a,由于点 B 的正面投影不可见,因此点 B 在六 棱柱后侧的铅垂面上。根据积聚性作出点 B 的水平投影 b。 2. 根据点 A 的水平投影 a 和正面投影 a′,按照“长对正、宽相等、高平齐”的投影规律 作出点 A 的侧面投影 a〞, 参见图 2.8(b)。 3. 根据点 B 的水平投影 b 和正面投影 b′,按照投影规律作出它的侧面投影 b〞,由于点 B 的侧面投影不可见,因此点 B 的侧面投影 b〞加括号,参见图 2.8(b)。 (a) (b) 图 2.8 习题 2 已知圆锥台曲面上的线 ABC 的正面投影,求作其侧面投影和水平投影(参见图 2.9 (a))。 解题分析:从图中可以看出该形体为轴线正垂线的半圆锥台。本题主要考查回转体的投影作 图以及圆锥台表面上线的投影,可以采用辅助圆法来解题。在线上应该选取一些特殊位置点 和一般位置点。本题中线上的特殊位置点包括最左点(最下点)A、最右点 C 以及最上点 B。 此外需要在点 A 和点 B 之间以及点 B 和点 C 之间选取一般位置点。将这些点在俯视图和左视 图中的投影确定好之后,光滑连线即得到线 ABC 的侧面投影和水平投影。 解题步骤: 1.由于 A、B、C 三点是特殊位置点,分别是最左点、最上点和最右点。利用辅助圆法先作 出这三点的水平投影 a、b、c 和侧面投影 a〞、b〞、c〞。以点 A 为例,过点 A 作正平 28