
第一章点线面 1.1学习要求 (1)学习正投影法的基本特性,掌握实形性、积聚性以及类似性。 (2)点、直线、平面作为基木几何元素,是本门课程的基础。堂据点、直线、平面的极型 规律以及它们之间的相对位置关系,为后续绘制工程图样奠定基础。 正确区分投影面 垂直线和投影面平行线的概念, 正确区分投影面垂直面和投影面平行面的概念。 (3)熟悉六面投影体系,绘制基本视图。 1.2内容简述 本章主要内容包括正投影法的基本概念及特性、点的投影规律、直线的投影规律、平面 的投影规律、六面投影体系以及六个基本视图(主视图、俯视图、左视图、仰视图、右视图 后视图)等。应熟悉直线与直线、直线与平面、平面与平面的相对位置关系。本章内容是本 门课程的基础理论知识。 1.2.1正投影法的基本特性 (1)实形性:平行于投影面的直线和平面,它们的投影能够反映其实际长度和实际形状。 (2)积聚性:垂直于投影平面的直线和平面,其投影积聚为一点和一直线。该特性是本门课 程经常使用的一个特性。 (3)类似性:倾斜于投影平面的直线和平面,其投影形状与其真实形状类似。利用类似性 可以辅助读图以及绘图 1.2.2点的投影 (1)点的投影仍然为点。空间点用大写字母表示,其水平投影用其小写字得表示,其正面 投影在小写字母基础上加一撤,其侧面投影在小写字母基础上加两撒。例如空间点A, 则其水平投影a,其正面投影a (2)点的两个投影间的连线垂直于相应的投影轴。点的正面投影和水平投影间的连线垂直 于X轴,点的正面投影和侧面投影间的连线垂直于Z轴,点的水平投影和侧面投影间 的连线沿投影面旋转而分别垂直于Y轴。 (3)点的各面投影到相应投影轴的距离,反映这个点到相应投影面的距离。点的正面投影 轴的 离能够反映这个点到水平投影面的距离。 点的正面投影到2轴的距离能 反映这个点到侧立投影面的距离。点的水平投影到X轴的距离能够反映这个点到正日 投影面的距离。点的水平投影到Y轴的距离能够反映这个点到侧立投影面的距离。点 的侧面投影到Y轴的距离能够反映这个点到水平投影面的距离。点的侧面投影到Z轴 的距离能铭反映这个占到正立投影面的距离 (4)根据两点之间的上下前后左右的空间位置, 确定点的投影。两点的x坐标决定了两点 的左右位置,两点的y坐标决定了两点的前后位置,两点的z坐标决定了两点的上下 位置。 (5)判断两点是否为重影点。空间两点A和B,如果它们的x和y坐标相同,z坐标不同。 则A和B在一条平行于Z轴的直线上。如果它们的x和艺华标相同,V坐标不同,则A 和B在一条平行于Y轴的直线上。如果它们的y和z坐标相同,x坐标不同,则A和B
第一章 点线面 1.1 学习要求 (1)学习正投影法的基本特性,掌握实形性、积聚性以及类似性。 (2)点、直线、平面作为基本几何元素,是本门课程的基础,掌握点、直线、平面的投影 规律以及它们之间的相对位置关系,为后续绘制工程图样奠定基础。正确区分投影面 垂直线和投影面平行线的概念,正确区分投影面垂直面和投影面平行面的概念。 (3)熟悉六面投影体系,绘制基本视图。 1.2 内容简述 本章主要内容包括正投影法的基本概念及特性、点的投影规律、直线的投影规律、平面 的投影规律、六面投影体系以及六个基本视图(主视图、俯视图、左视图、仰视图、右视图、 后视图)等。应熟悉直线与直线、直线与平面、平面与平面的相对位置关系。本章内容是本 门课程的基础理论知识。 1.2.1 正投影法的基本特性 (1)实形性:平行于投影面的直线和平面,它们的投影能够反映其实际长度和实际形状。 (2)积聚性:垂直于投影平面的直线和平面,其投影积聚为一点和一直线。该特性是本门课 程经常使用的一个特性。 (3)类似性:倾斜于投影平面的直线和平面, 其投影形状与其真实形状类似。利用类似性 可以辅助读图以及绘图。 1.2.2 点的投影 (1)点的投影仍然为点。空间点用大写字母表示,其水平投影用其小写字母表示,其正面 投影在小写字母基础上加一撇,其侧面投影在小写字母基础上加两撇。例如空间点 A, 则其水平投影 a,其正面投影 a′,其侧面投影 a〞。 (2)点的两个投影间的连线垂直于相应的投影轴。点的正面投影和水平投影间的连线垂直 于 X 轴,点的正面投影和侧面投影间的连线垂直于 Z 轴,点的水平投影和侧面投影间 的连线沿投影面旋转而分别垂直于 Y 轴。 (3)点的各面投影到相应投影轴的距离,反映这个点到相应投影面的距离。点的正面投影 到 X 轴的距离能够反映这个点到水平投影面的距离。点的正面投影到 Z 轴的距离能够 反映这个点到侧立投影面的距离。点的水平投影到 X 轴的距离能够反映这个点到正立 投影面的距离。点的水平投影到 Y 轴的距离能够反映这个点到侧立投影面的距离。点 的侧面投影到 Y 轴的距离能够反映这个点到水平投影面的距离。点的侧面投影到 Z 轴 的距离能够反映这个点到正立投影面的距离。 (4)根据两点之间的上下前后左右的空间位置,确定点的投影。两点的 x 坐标决定了两点 的左右位置,两点的 y 坐标决定了两点的前后位置,两点的 z 坐标决定了两点的上下 位置。 (5)判断两点是否为重影点。空间两点 A 和 B,如果它们的 x 和 y 坐标相同,z 坐标不同, 则 A 和 B 在一条平行于 Z 轴的直线上。如果它们的 x 和 z 坐标相同,y 坐标不同,则 A 和 B 在一条平行于 Y 轴的直线上。如果它们的 y 和 z 坐标相同,x 坐标不同,则 A 和 B 1

在一条平行于X轴的直线上。 1.2.3直线的投影 (1)直线的投影一般为直线,特殊情况积聚为一点。直线的投影由直线上两个点的投影确 定。如果直线上有一个点,则该点的投影必然在直线的同面投影上。 (2)凡垂直于某一投影面.同时平行于另两个投影面的直线统称为投影面的垂直线。投影面 垂直线在与其所垂直的投影面上的投影积聚为 一点,其余两个投影均垂直于相应的投 影轴且反映该直线的实长。投影面垂直线分为三种:正垂线、铅垂线、 ,垂直 于正投影面的称为正垂线,垂直于水平投影面的称为铅垂线,垂直于侧投影面的称为 侧垂线。正垂线在正立投影面上的投影积聚为一点,在水平投影面和侧立投影面的投 影反映实长而且垂直于相应的投影轴。铅垂线在水平投影面上的投影积聚为一点,在 正立投影面和侧立投影面的投影反映实长而且垂直于相应的投影轴。侧垂线在侧立投 影面上的投影积聚为一点,在正立投影面和水平投影面的投影反映实长而且垂直于相 应的投影轴。 (3)凡平行于某一投影面,同时倾斜于另两个投影面的直线统称为投影面的平行线。投楚 面平行线在与其所平行的投影面上的投影反映该直线的实长,其余两个投影均分别平 行于相应的投影轴。投影面平行线分为三种:正平线、水平线、侧平线。平行于正投 影面的称为正平线,平行于水平投影面的称为水平线,平行于侧投影面的称为侧平线。 正平线在正立投影面上的投影能够反映实长 正平线与水平投影面的真实夹角及其 侧立投影面的真实夹角。水平线在水平投影面上的投影能够反映实长、水平线与正 投影面的真实夹角及其与侧立投影面的真实夹角。侧平线在侧立投影面上的投影能够 反映实长、侧平线与正立投影面的真实夹角及其与水平投影面的直实夹角。 (④)既不垂直也不平行于任一基本投影面的直线称为一般位置直线。 一般位置线的任 投影均不 反映该直 线的实长 而且小于实长 电不能积聚为 点。而且任一投影与投 影轴的夹角也不能反映该空间直线与任一基本投影面的真实夹角。 (5)直线与直线的相对位置关系:平行,相交,交叉。两个直线平行,它们的同面投影必 然相互平行。两个直线相交,它们它们的各面投影必然相交。 1.2.4平面的投影 (1)凡垂直于 一个投影面,而与另两个投影面倾斜的平面称为投影面的垂直面。投影面垂 直面在与其所垂直的投影面上的投影积聚为一直线。投影面垂直面分为三种:正垂面、 铅垂而、侧垂面。垂直于正立投影面的称为正垂面,垂直于水平投影面的称为铅垂面, 垂直于侧立投影面的称为侧垂面。正垂面在正立投影面的投影积聚为一条直线,并能 反映正垂面与水平投影面的夹角和其与侧立投影面的夹角。正垂面在 平投影面和侧 立投影面的投影是原始形状的类以形。铅垂面在水平投影面的投影积聚为一条直线 并能反映铅垂面与正立投影面的夹角和其与侧立投影面的夹角。铅垂面在正立投影面 和侧立投影面的投影是原始形状的类似形。侧垂面在侧立投影面的投影积聚为一条直 线,并能反映侧垂面与正立投影面的夹角和其与水平投影面的夹角。侧垂面在正立投 影面和水平投影面的投影是原始形状的类似形。 (2)凡平行于某一个投影面,同时垂直于另两个投影面的平面统称为投影面的平行面。投 影面平行面在与其平行的的投影面上的投影反映该平面的真实形状。投影面平行面分 为三种:正平面、水平面、侧平面。平行于正立投影面的称为正平面,平行于水平投 影面的称为水平面,平行于侧立投影面的称为侧平面。正平面在正立投影面的投影能
在一条平行于 X 轴的直线上。 1.2.3 直线的投影 (1)直线的投影一般为直线,特殊情况积聚为一点。直线的投影由直线上两个点的投影确 定。如果直线上有一个点,则该点的投影必然在直线的同面投影上。 (2)凡垂直于某一投影面,同时平行于另两个投影面的直线统称为投影面的垂直线。投影面 垂直线在与其所垂直的投影面上的投影积聚为一点,其余两个投影均垂直于相应的投 影轴且反映该直线的实长。投影面垂直线分为三种:正垂线、铅垂线、侧垂线。垂直 于正投影面的称为正垂线,垂直于水平投影面的称为铅垂线,垂直于侧投影面的称为 侧垂线。正垂线在正立投影面上的投影积聚为一点,在水平投影面和侧立投影面的投 影反映实长而且垂直于相应的投影轴。铅垂线在水平投影面上的投影积聚为一点,在 正立投影面和侧立投影面的投影反映实长而且垂直于相应的投影轴。侧垂线在侧立投 影面上的投影积聚为一点,在正立投影面和水平投影面的投影反映实长而且垂直于相 应的投影轴。 (3)凡平行于某一投影面,同时倾斜于另两个投影面的直线统称为投影面的平行线。投影 面平行线在与其所平行的投影面上的投影反映该直线的实长,其余两个投影均分别平 行于相应的投影轴。投影面平行线分为三种:正平线、水平线、侧平线。平行于正投 影面的称为正平线,平行于水平投影面的称为水平线,平行于侧投影面的称为侧平线。 正平线在正立投影面上的投影能够反映实长、正平线与水平投影面的真实夹角及其与 侧立投影面的真实夹角。水平线在水平投影面上的投影能够反映实长、水平线与正立 投影面的真实夹角及其与侧立投影面的真实夹角。侧平线在侧立投影面上的投影能够 反映实长、侧平线与正立投影面的真实夹角及其与水平投影面的真实夹角。 (4)既不垂直也不平行于任一基本投影面的直线称为一般位置直线。一般位置直线的任一 投影均不反映该直线的实长,而且小于实长,也不能积聚为一点。而且任一投影与投 影轴的夹角也不能反映该空间直线与任一基本投影面的真实夹角。 (5)直线与直线的相对位置关系:平行,相交,交叉。两个直线平行,它们的同面投影必 然相互平行。两个直线相交,它们它们的各面投影必然相交。 1.2.4 平面的投影 (1)凡垂直于一个投影面,而与另两个投影面倾斜的平面称为投影面的垂直面。投影面垂 直面在与其所垂直的投影面上的投影积聚为一直线。投影面垂直面分为三种:正垂面、 铅垂面、侧垂面。垂直于正立投影面的称为正垂面,垂直于水平投影面的称为铅垂面, 垂直于侧立投影面的称为侧垂面。正垂面在正立投影面的投影积聚为一条直线,并能 反映正垂面与水平投影面的夹角和其与侧立投影面的夹角。正垂面在水平投影面和侧 立投影面的投影是原始形状的类似形。铅垂面在水平投影面的投影积聚为一条直线, 并能反映铅垂面与正立投影面的夹角和其与侧立投影面的夹角。铅垂面在正立投影面 和侧立投影面的投影是原始形状的类似形。侧垂面在侧立投影面的投影积聚为一条直 线,并能反映侧垂面与正立投影面的夹角和其与水平投影面的夹角。侧垂面在正立投 影面和水平投影面的投影是原始形状的类似形。 (2)凡平行于某一个投影面,同时垂直于另两个投影面的平面统称为投影面的平行面。投 影面平行面在与其平行的的投影面上的投影反映该平面的真实形状。投影面平行面分 为三种:正平面、水平面、侧平面。平行于正立投影面的称为正平面,平行于水平投 影面的称为水平面,平行于侧立投影面的称为侧平面。正平面在正立投影面的投影能 2

够反映真实形状。在水平投影面和侧立投影面都积聚成直线,且其水平投影和侧立投 影分别平行于相应的投影轴。水平面在水平投影面的投影能够反映实形状。在正立 新,面和侧立投影面都积聚成直线,且其正面投影和侧立投影分别平平投影面都 。侧平面在侧立投影面的投影能够反映真实形状。在正立 聚成直线,且其正面投影和水平投影分别平行于相应的投影轴。 (3)同时倾斜于三个投影面的平面称为一般位置平面。一般位置平面的三个投影均不反映 平面的实际形状,都是其原始形状的类似形。 1.2.5直线与平面的位置关系 直线与平面之间的位置关系分为平行、相交以及垂直。如果平面外的一条直线平行于平 面内的一条直线,那么该直线就与这个平面平行。当平面在某一投影面上的投影积聚为一条 有线时,则直线和平面在该投影面上的投影百相平行,有线与平面相交时,共有占就县交占」 需要注意直线被平面遮挡的部分。如果直线与平面垂直,那么这条直线与平面内的所有直线 均垂直。当平面与某一投影面垂直时,则直线与平面在该投影面上的投影互相垂直, 1.2.6六面投影体系 (1)六个基本投影面是V面、V面、H面、H面、面、黑面 (2)六个基本视图 一主视图、俯视图、左视图 仰视图、右视图、后视图。主视图为从前 向后投影在相应投影面的视图,俯视图为从上向下投影在相应投影面的视图,左视图 为从左向右投影在相应投影面的视图,仰视图为从下向上投影在相应投影面的视图, 右视图为从右向左投影在相应投影面的视图,后视图为从后向前投影在相应投影面的 视图。俯视图在主视图的正下方,左视图在主视图的正右方,右视图在在主视图的正 :方 仰视图在 视图的 后视图在左视图的正右方 (3) 六面基本视图间的投影规律:长对正,宽相等,高平齐。 主视图、俯视图、仰视图长对正,与后视图长对准,左视图、右视图、仰视图、俯视 图宽相等,主视图、左视图、右视图、后视图高平齐。 (4)主视图反映了物体的长度和高度,俯视图反映了物体的长度和宽度,左视图反映了物 体的宽度和高度,仰视图反映了物体的长度和宽度,右视图反映了物体的宽度和高度, 后视图反映 物体 的长度和高度。 主视图反映 了物体的 、下 右方位 长系, 视图反映了物体的上、下、前、后方位关系,俯视图反映了物体的左、右、前、后方 位关系,右视图反映了物体的上、下、前、后方位关系,仰视图反映了左、右、前、 后方位关系,后视图反映了上、下、左、右方位关系。 1.3本章知识点 (1)正投影法原理。 (2)点的投影。 (3)直线的投影 (4)平面的投影, (5)绘制基本视图 1.4思考题 (1)沿投影方向移动物体,其正投影的大小变不变? 3
够反映真实形状。在水平投影面和侧立投影面都积聚成直线,且其水平投影和侧立投 影分别平行于相应的投影轴。水平面在水平投影面的投影能够反映真实形状。在正立 投影面和侧立投影面都积聚成直线,且其正面投影和侧立投影分别平行于相应的投影 轴。侧平面在侧立投影面的投影能够反映真实形状。在正立投影面和水平投影面都积 聚成直线,且其正面投影和水平投影分别平行于相应的投影轴。 (3)同时倾斜于三个投影面的平面称为一般位置平面。一般位置平面的三个投影均不反映 平面的实际形状,都是其原始形状的类似形。 1.2.5 直线与平面的位置关系 直线与平面之间的位置关系分为平行、相交以及垂直。如果平面外的一条直线平行于平 面内的一条直线,那么该直线就与这个平面平行。当平面在某一投影面上的投影积聚为一条 直线时,则直线和平面在该投影面上的投影互相平行。直线与平面相交时,共有点就是交点, 需要注意直线被平面遮挡的部分。如果直线与平面垂直,那么这条直线与平面内的所有直线 均垂直。当平面与某一投影面垂直时,则直线与平面在该投影面上的投影互相垂直。 1.2.6 六面投影体系 (1)六个基本投影面是 V 面、V1面、H 面、H1面、W 面、W1面。 (2)六个基本视图—主视图、俯视图、左视图、仰视图、右视图、后视图。主视图为从前 向后投影在相应投影面的视图,俯视图为从上向下投影在相应投影面的视图,左视图 为从左向右投影在相应投影面的视图,仰视图为从下向上投影在相应投影面的视图, 右视图为从右向左投影在相应投影面的视图,后视图为从后向前投影在相应投影面的 视图。俯视图在主视图的正下方,左视图在主视图的正右方,右视图在在主视图的正 左方,仰视图在主视图的正上方,后视图在左视图的正右方。 (3)六面基本视图间的投影规律:长对正,宽相等,高平齐。 主视图、俯视图、仰视图长对正,与后视图长对准,左视图、右视图、仰视图、俯视 图宽相等,主视图、左视图、右视图、后视图高平齐。 (4)主视图反映了物体的长度和高度,俯视图反映了物体的长度和宽度,左视图反映了物 体的宽度和高度,仰视图反映了物体的长度和宽度,右视图反映了物体的宽度和高度, 后视图反映了物体的长度和高度。主视图反映了物体的上、下、左、右方位关系,左 视图反映了物体的上、下、前、后方位关系,俯视图反映了物体的左、右、前、后方 位关系,右视图反映了物体的上、下、前、后方位关系,仰视图反映了左、右、前、 后方位关系,后视图反映了上、下、左、右方位关系。 1.3 本章知识点 (1)正投影法原理。 (2)点的投影。 (3)直线的投影。 (4)平面的投影。 (5)绘制基本视图。 1.4 思考题 (1)沿投影方向移动物体,其正投影的大小变不变? 3

(2)物体的正投影是否可能反映某一个面的实形? (3)六个基本视图中哪些视图能反映物体的宽度和高度? (4)正投影法的投影特性是什么 (5)铅垂面、正垂面以及侧垂面本别在哪个投影面上的投影积聚为一条直线? 1.5例题与习题解答 1.5.1例题 例1已知三点D、E、F的两面投影,求作这三个点在第三个投影面上的投影(参见图1.1 (a))。 f月 解题分析:本题目主要考查根据空间点的两面投影求作第三面投影的绘图过程。从已知图中 可以看出点D和点E的已知投影为正面投影和水平投感,需要作侧侧面投影。点F己知投影 为正面投影和侧面投影,需要作水平投影。此外根据点D的正面投影和水平投影可以分析点 D位于正立投影面中,根据点F的正面投影和侧面投影可以分析点F位于侧立投影面中。 解题步骤: 4
(2)物体的正投影是否可能反映某一个面的实形? (3)六个基本视图中哪些视图能反映物体的宽度和高度? (4)正投影法的投影特性是什么? (5)铅垂面、正垂面以及侧垂面本别在哪个投影面上的投影积聚为一条直线? 1.5 例题与习题解答 1.5.1 例题 例 1 已知三点 D、E、F 的两面投影,求作这三个点在第三个投影面上的投影(参见图 1.1 (a))。 (a) (b) 图 1.1 解题分析:本题目主要考查根据空间点的两面投影求作第三面投影的绘图过程。从已知图中 可以看出点 D 和点 E 的已知投影为正面投影和水平投影,需要作侧面投影。点 F 已知投影 为正面投影和侧面投影,需要作水平投影。此外根据点 D 的正面投影和水平投影可以分析点 D 位于正立投影面中,根据点 F 的正面投影和侧面投影可以分析点 F 位于侧立投影面中。 解题步骤: 4

1.从原点0向左下方作45°辅助线。 2.过作垂直于投影轴YH轴的垂线,得到与45”辅助线的交点0,过点0作投影轴Y轴 的垂线, 再过d'作投影轴Z轴的垂线,两条垂线的交点就是所求的d (参见图1.】 (b) 3.过e作投影轴Yu轴的垂线并延长,得到与45°辅助线的交点,过这个交点作投影轴Y 轴的垂线,再过e'作投影轴Z轴的垂线,两条垂线的交点就是所求的e”(参见图1.1 (b)). 4.过个作投影轴Y轴的垂线并延长,得到与45°辅助线的交点,过这个交点作投影轴 Y轴的垂线,再过f'作投影轴X轴的垂线,两条垂线的交点就是所求的f(参见图1.1 (b))。 例2己知直线EF为正平线,它与正面的距离为25m,求作直线F在水平面、侧面上的投影(参 见图1.2(a)。 解题分析:由于直线F为正平线,因磁漆在正面的投影反映实长,其在水平投影面上的投影 应该平行于X轴,其在侧立投影面上的投影应该平行于Z轴。 解顾步骤: 1.题目中指出直线F与正面的距离为2 ,因此按照“长对正”的投影规律在距离X轴25m 处作出直线F的在水平面上的投影ef 2.根据直线F的正面投影e'f'以及水平投影ef,作出直线的侧面投影e”f”,参见图1.2 (b). (b) 图1.2 例3已知直线DE在平面ABC内,作出直线DE的水平投影(参见图1.3(a) 解题分析:本题考查了线在平面内,属于平面内的点和线的投影问题。由已知条件可知直线 5
1. 从原点 O 向左下方作 45°辅助线。 2. 过 d 作垂直于投影轴 YH 轴的垂线,得到与 45°辅助线的交点 O,过点 O 作投影轴 Yw 轴 的垂线,再过 d′作投影轴 Z 轴的垂线,两条垂线的交点就是所求的 d〞(参见图 1.1 (b))。 3. 过 e 作投影轴 YH轴的垂线并延长,得到与 45°辅助线的交点,过这个交点作投影轴 Yw 轴的垂线,再过 e′作投影轴 Z 轴的垂线,两条垂线的交点就是所求的 e〞(参见图 1.1 (b))。 4. 过 f〞作投影轴 Yw 轴的垂线并延长,得到与 45°辅助线的交点,过这个交点作投影轴 YH轴的垂线,再过 f′作投影轴 X 轴的垂线,两条垂线的交点就是所求的 f(参见图 1.1 (b))。 例2 已知直线EF为正平线,它与正面的距离为25mm,求作直线EF在水平面、侧面上的投影(参 见图1.2(a))。 解题分析:由于直线EF为正平线,因磁漆在正面的投影反映实长,其在水平投影面上的投影 应该平行于X轴,其在侧立投影面上的投影应该平行于Z轴。 解题步骤: 1. 题目中指出直线EF与正面的距离为25mm,因此按照“长对正”的投影规律在距离X轴25mm 处作出直线EF的在水平面上的投影ef。 2. 根据直线EF的正面投影e′f′以及水平投影ef,作出直线的侧面投影e〞f〞,参见图1.2 (b)。 (a) (b) 图 1.2 例3 已知直线DE在平面ABC内,作出直线DE的水平投影(参见图1.3(a))。 解题分析:本题考查了线在平面内,属于平面内的点和线的投影问题。由已知条件可知直线 5
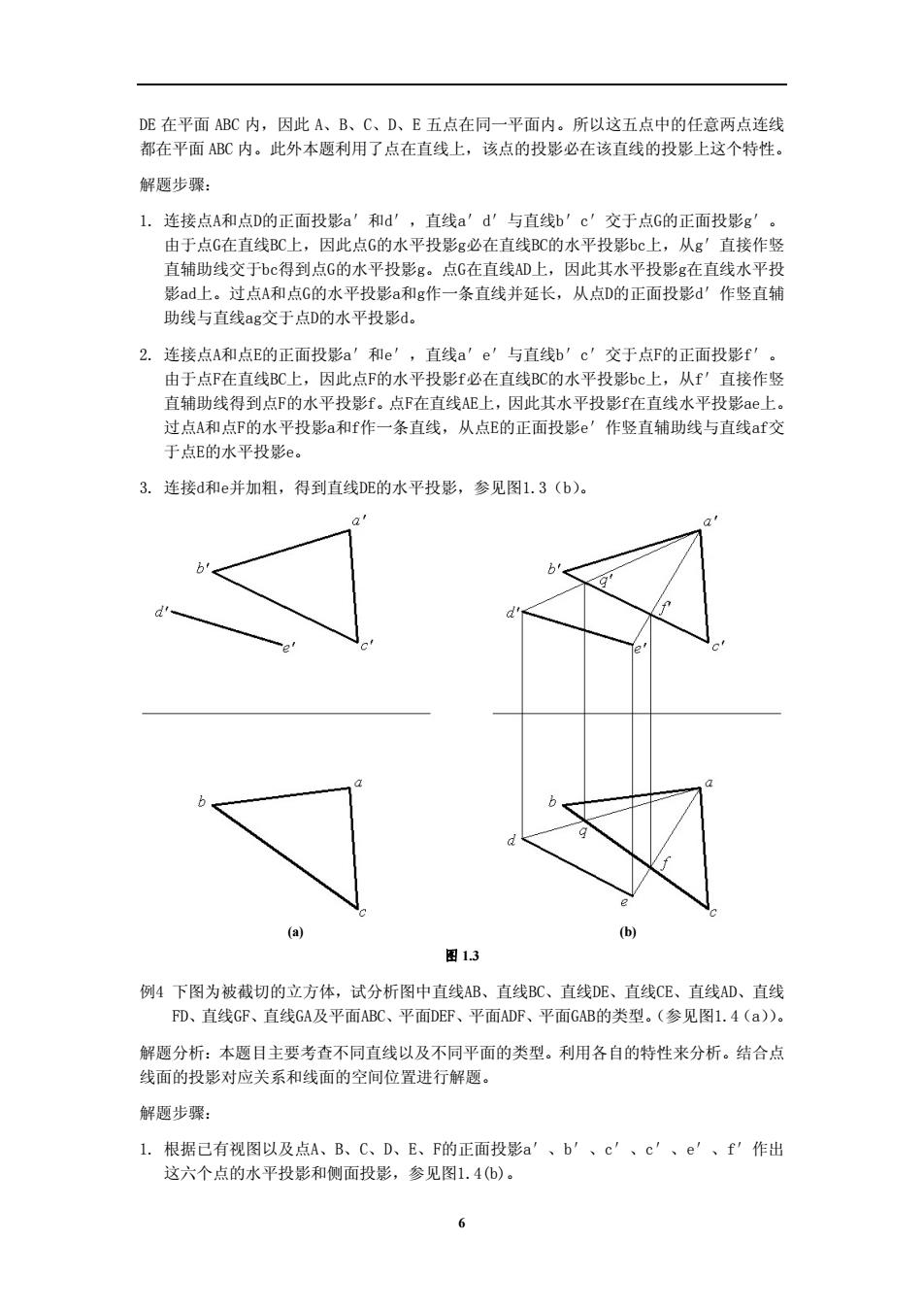
DE在平面ABC内,因此A、B、C、D、E五点在同一平面内。所以这五点中的任意两点连线 都在平面ABC内。此外本题利用了点在直线上,该点的投影必在该直线的投影上这个特性。 解题步骤: 1.连接点A和点D的正面投影a'和d',直线a'd'与直线b'c'交于点G的正面投影g' 由于点G在直线C上,因此点G的水平投影g必在直线BC的水平投影bC上,从g'直接作竖 直辅助线交于bC得到点G的水平投影g。点G在直线D上,因此其水平投影g在直线水平投 影ad上。过点A和点G的水平投影a和g作一条直线并延长,从点D的正面投影d'作竖直辅 助线与直线ag交于点D的水平投影d。 2.连接点A和点E的正面投影a'和e',直线a'e'与直线b'c'交于点F的正面投影f' 由于点F在直线C上,因此点F的水平投影f必在直线BC的水平投影bc上,从f'直接作竖 直辅助线得到点F的水平投影f。点F在直线AE上,因此其水平投影f在直线水平投影ae上。 过点A和点F的水平投影a和f作一条直线,从点E的正面投影e'作竖直辅助线与直线af交 于点E的水平投影e。 3.连接d和e并加粗,得到直线DE的水平投影,参见图1.3(b)。 b 图13 例4下图为被截切的立方体,试分析图中直线AB、直线C、直线DE、直线CE、直线AD、直线 D、直线GR、直线GA及平面ABC、平面DEF、平面ADF、平面GAB的类型。(参见图1,4(a)。 解题分析:本题目主要考查不同直线以及不同平面的类型。利用各自的特性来分析。结合点 线面的投影对应关系和线面的空间位置进行解题。 解题步骤: 1.根据已有视图以及点A、B、C、D、E、F的正面投影a'、b'、c'、c'、e'、f'作出 这六个点的水平投影和侧面投影,参见图1.4(b)
DE 在平面 ABC 内,因此 A、B、C、D、E 五点在同一平面内。所以这五点中的任意两点连线 都在平面 ABC 内。此外本题利用了点在直线上,该点的投影必在该直线的投影上这个特性。 解题步骤: 1. 连接点A和点D的正面投影a′和d′,直线a′d′与直线b′c′交于点G的正面投影g′。 由于点G在直线BC上,因此点G的水平投影g必在直线BC的水平投影bc上,从g′直接作竖 直辅助线交于bc得到点G的水平投影g。点G在直线AD上,因此其水平投影g在直线水平投 影ad上。过点A和点G的水平投影a和g作一条直线并延长,从点D的正面投影d′作竖直辅 助线与直线ag交于点D的水平投影d。 2. 连接点A和点E的正面投影a′和e′,直线a′e′与直线b′c′交于点F的正面投影f′。 由于点F在直线BC上,因此点F的水平投影f必在直线BC的水平投影bc上,从f′直接作竖 直辅助线得到点F的水平投影f。点F在直线AE上,因此其水平投影f在直线水平投影ae上。 过点A和点F的水平投影a和f作一条直线,从点E的正面投影e′作竖直辅助线与直线af交 于点E的水平投影e。 3. 连接d和e并加粗,得到直线DE的水平投影,参见图1.3(b)。 (a) (b) 图 1.3 例4 下图为被截切的立方体,试分析图中直线AB、直线BC、直线DE、直线CE、直线AD、直线 FD、直线GF、直线GA及平面ABC、平面DEF、平面ADF、平面GAB的类型。(参见图1.4(a))。 解题分析:本题目主要考查不同直线以及不同平面的类型。利用各自的特性来分析。结合点 线面的投影对应关系和线面的空间位置进行解题。 解题步骤: 1. 根据已有视图以及点A、B、C、D、E、F的正面投影a′、b′、c′、c′、e′、f′作出 这六个点的水平投影和侧面投影,参见图1.4(b)。 6

2.直线AB的水平投影b平行于X轴,其侧面投影a”c”平行于Z轴。可以分析出直线B平行 于正面,倾斜于水平面和侧面,因此为正平线。直线C的水平投影红平行于X轴,其正面 侧面投影”c”积聚为一点。由此可以分析出直线BC垂直于侧 平行于水平面和正面,因此为侧垂线。直线DE的水平投影de平行于X轴, 其正面投 d'e'平行于X轴,侧面投影d”e”积聚为一点。由此可以分析出直线DE垂直于侧面 平行于水平面和正面,因此为侧垂线。直线CE的水平投影ce积聚为一点,它的正面投影 c'e'平行于Z轴,侧面投影c”e”平行于Z轴。由此可以分析出直线CE垂直于水平面, 平行于正面和侧面,因此为铅垂线。直线D的水平投影d积聚为一点,它的正面投影 d'平行于Z轴, 侧面投影a”d”平行于z轴, 由此可以分析出直线AD垂直于水平面 平行于正面和侧面,因此为铅垂线。直线D的正面投影f'd'积聚为 一点,它的水平投 影f平行于Y轴,侧面投影f”d”平行于Y轴。由此可以分析出直线FD垂直于正面,平行 于水平面和侧面,因此为正垂线。直线GF的水平投影g积聚为一点,它的正面投影gf平 行于轴,侧面投影g””平行于?轴。由此可以分析出直线GF垂直于水平面,平行于正 面和侧面,因此为铅垂线。直线GA的正面投影g'a'积聚为一点,它的水平投影ga平行 于Y轴,侧面投影g”a”平行于Y轴。由此可以分析出直线GA垂直于正面,平行于水平面 和侧面,因此为正垂线。 3.平面BC的水平投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线,而 且平行于Z轴,由此可以分析出平面BC与正面平行,与水平面和侧面垂直,所以为正平 面。平面DF的正面投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线, 而且平行于Y轴,由此可以分析出平面与水平面平行,与正面和侧面垂直,因此为水 平面。平面ADF的水平投影积聚为一条直线,而且平行于Y轴,其正面投影积聚为一条直 线,而且平行于Z轴,由此可以分析出平面ADF与侧面平行,与水平面和正面垂直,所以 为侧平面。平面GAB的正面投影积聚为一条倾斜直线,其水平面投影为gab,侧面投影为 a”b”。由此可以分析出平面GAB垂直于正面,倾斜于水平面和正面,所以为正垂面 图1d 1.5.2习题及答案 习题1已知点A在点B之前4毫米,之上10毫米,之右8毫米,求A点的投影(参见图1.5 (a). 解题分析:从己知图中可以看出点B的三面投影是已知的,需要根据点A和点B之间的空间 位置关系来确定点A的投影。此题主要通过两点之间的相对位置来进行解题。 >
2. 直线AB的水平投影ab平行于X轴,其侧面投影a〞c〞平行于Z轴。可以分析出直线AB平行 于正面,倾斜于水平面和侧面,因此为正平线。直线BC的水平投影bc平行于X轴,其正面 投影b′c′平行于X轴, 侧面投影b〞c〞积聚为一点。由此可以分析出直线BC垂直于侧 面,平行于水平面和正面,因此为侧垂线。直线DE的水平投影de平行于X轴,其正面投影 d′e′平行于X轴, 侧面投影d〞e〞积聚为一点。由此可以分析出直线DE垂直于侧面, 平行于水平面和正面,因此为侧垂线。直线CE的水平投影ce积聚为一点,它的正面投影 c′e′平行于Z轴, 侧面投影c〞e〞平行于Z轴。由此可以分析出直线CE垂直于水平面, 平行于正面和侧面,因此为铅垂线。直线AD的水平投影ad积聚为一点,它的正面投影 a′d′平行于Z轴, 侧面投影a〞d〞平行于Z轴。由此可以分析出直线AD垂直于水平面, 平行于正面和侧面,因此为铅垂线。直线FD的正面投影f′d′积聚为一点,它的水平投 影fd平行于Y轴, 侧面投影f〞d〞平行于Y轴。由此可以分析出直线FD垂直于正面,平行 于水平面和侧面,因此为正垂线。直线GF的水平投影gf积聚为一点,它的正面投影gf平 行于Z轴, 侧面投影g〞f〞平行于Z轴。由此可以分析出直线GF垂直于水平面,平行于正 面和侧面,因此为铅垂线。直线GA的正面投影g′a′积聚为一点,它的水平投影ga平行 于Y轴, 侧面投影g〞a〞平行于Y轴。由此可以分析出直线GA垂直于正面,平行于水平面 和侧面,因此为正垂线。 3. 平面ABC的水平投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线,而 且平行于Z轴,由此可以分析出平面ABC与正面平行,与水平面和侧面垂直,所以为正平 面。平面DEF的正面投影积聚为一条直线,而且平行于X轴,其侧面投影积聚为一条直线, 而且平行于Y轴,由此可以分析出平面DEF与水平面平行,与正面和侧面垂直,因此为水 平面。平面ADF的水平投影积聚为一条直线,而且平行于Y轴,其正面投影积聚为一条直 线,而且平行于Z轴,由此可以分析出平面ADF与侧面平行,与水平面和正面垂直,所以 为侧平面。平面GAB的正面投影积聚为一条倾斜直线,其水平面投影为gab,侧面投影为 g〞a〞b〞。由此可以分析出平面GAB垂直于正面,倾斜于水平面和正面,所以为正垂面。 (a) (b) 图 1.4 1.5.2 习题及答案 习题 1 已知点 A 在点 B 之前 4 毫米,之上 10 毫米,之右 8 毫米,求 A 点的投影(参见图 1.5 (a))。 解题分析:从已知图中可以看出点 B 的三面投影是已知的,需要根据点 A 和点 B 之间的空间 位置关系来确定点 A 的投影。此题主要通过两点之间的相对位置来进行解题。 7

解题步骤: 1.由于点A在点B的前方4毫米,因此从点B的水平投影b向下量出4m,作一条平行于 X轴的直线。点A在点B的右方8毫米,因此从点B的水平投影b向右量出8m,作 条平行于YH轴的直线。两条直线的交点就是点A的水平投影a。 2.由于点A在点B的上方10毫米,因此从点B的正面投影b'向上量出10mm,作一条平 行于X轴的直线。这条直线与前边作的第二条直线的交点就是点A的正面投影a'。 3.通过点A的水平投影a和正面投影a',作出侧面投影a”,参见图l.5(b)。 Z b) 图1.5 习题2已知点A的水平投影和正面投影,求作其侧面投影。点B在点A之上10m,左I0mm,前 10mm,求作点B的正面投影,水平投影和侧面投影。(参见图1.6(a)。 图1.6 解题分析:从图中可以根据点A的水平投影和正面投影,作出其侧面投影。然后再根据两点 间的相对位置关系来确定点B的三面投影。 解题步骤: 1.根据点A的水平投影和正面投影,作点A的侧面投影。过点A的水平投影a作平行于X 轴的直线,与从原点出发的4 辅助线交于一点,过这点作垂直于Y轴的直线,再从点 A的正面投影a'作平行于X轴的直线,这两条直线的交点就是点A的侧面投影a”。 2.由于点B在点A的上方10m,左侧10,因此在点A的正面投影a'上方10m处作一条
解题步骤: 1. 由于点 A 在点 B 的前方 4 毫米,因此从点 B 的水平投影 b 向下量出 4mm,作一条平行于 X 轴的直线。点 A 在点 B 的右方 8 毫米,因此从点 B 的水平投影 b 向右量出 8mm,作一 条平行于 YH 轴的直线。两条直线的交点就是点 A 的水平投影 a。 2. 由于点 A 在点 B 的上方 10 毫米,因此从点 B 的正面投影 b′向上量出 10mm,作一条平 行于 X 轴的直线。这条直线与前边作的第二条直线的交点就是点 A 的正面投影 a′。 3. 通过点 A 的水平投影 a 和正面投影 a′,作出侧面投影 a〞, 参见图 1.5(b)。 (a) (b) 图 1.5 习题2 已知点A的水平投影和正面投影,求作其侧面投影。点B在点A之上10mm,左10mm,前 10mm,求作点B的正面投影,水平投影和侧面投影。(参见图1.6(a))。 (a) (b) 图 1.6 解题分析:从图中可以根据点 A 的水平投影和正面投影,作出其侧面投影。然后再根据两点 间的相对位置关系来确定点 B 的三面投影。 解题步骤: 1. 根据点 A 的水平投影和正面投影,作点 A 的侧面投影。过点 A 的水平投影 a 作平行于 X 轴的直线,与从原点出发的 45°辅助线交于一点,过这点作垂直于 Y 轴的直线,再从点 A 的正面投影 a′作平行于 X 轴的直线,这两条直线的交点就是点 A 的侧面投影 a〞。 2. 由于点 B 在点 A 的上方 10mm,左侧 10mm, 因此在点 A 的正面投影 a′上方 10mm 处作一条 8

平行于X轴的直线,然后在点A的正面投影a'左侧10m处作一条平行于Y轴的直线, 两条直线的交点就是点B的正面投影b'。 3.由于点B在点A的前方10m,因此在点A的水平投影a前方作作出一条平行于X轴的直 线,然后过点B的正面投影b'作一条平行于Y轴的直线,两条直线的交点就是点B的 的水平投影b。 4.根据点B的正面投影b'和水平投影b,作出侧面投影b”。过点B的水平投影b作平行 于X轴的直线,与从原占出发的45·辅助线交于一占,过这占作垂直于V轴的直线,再 从点B的正面投影b'作平行于X轴的直线,这两条直线的交点就是点B的侧面投影 ,参见图1.6(0. 习题3已知线段AB是正垂线,A点在B点的前部,AB长度为15m,距离水平投影面2Omm,B点 距离正立投影面30m,作出线段B的正面投影和水平投影。 解题分析:本题主要利用正垂线的投影特性进行解题。正垂线在正立投影面的投影积聚为 点。在水平投影面的投影垂直于X轴 解题步骤: 1.由于直线B是正垂线,因此在正立投影面的投影积聚为一点。直线4B距离水平投影面 2O,而且A点在B点前部,B点被遮挡,作出直线AB的正面投影a'(b')。 2.由于直线B上B端点距离正立投影面30mm,根据投影关系作出点B的水平投影, 3.根据直线AB长度为15m,作出点A的水平投影a,直线AB的正面投影和水平投影参见图 1.7。 图1.7 习题4三角形ABC中AB为水平线,BC为正平线,补全三角形ABC的投影(参见图1.8(a)。 解题分析:本题主要利用水平线和正平线的投影特性进行解题。水平线的正面投影平行于X 轴。正平线的水平投影平行于X轴。如若求三角形ABC的投影,只要将三角形的三条边的投影 作出,即可得到三角形ABC的投影。 9
平行于 X 轴的直线,然后在点 A 的正面投影 a′左侧 10mm 处作一条平行于 Y 轴的直线, 两条直线的交点就是点 B 的正面投影 b′。 3. 由于点 B 在点 A 的前方 10mm,因此在点 A 的水平投影 a 前方作作出一条平行于 X 轴的直 线,然后过点 B 的正面投影 b′作一条平行于 Y 轴的直线,两条直线的交点就是点 B 的 的水平投影 b。 4. 根据点 B 的正面投影 b′和水平投影 b,作出侧面投影 b〞。过点 B 的水平投影 b 作平行 于 X 轴的直线,与从原点出发的 45°辅助线交于一点,过这点作垂直于 Y 轴的直线,再 从点 B 的正面投影 b′作平行于 X 轴的直线,这两条直线的交点就是点 B 的侧面投影 b〞。参见图 1.6(b)。 习题3 已知线段AB是正垂线,A点在B点的前部,AB长度为15mm,距离水平投影面20mm,B点 距离正立投影面30mm,作出线段AB的正面投影和水平投影。 解题分析:本题主要利用正垂线的投影特性进行解题。正垂线在正立投影面的投影积聚为一 点。在水平投影面的投影垂直于X轴。 解题步骤: 1. 由于直线AB是正垂线,因此在正立投影面的投影积聚为一点。直线AB距离水平投影面 20mm,而且A点在B点前部,B点被遮挡,作出直线AB的正面投影a′(b′)。 2. 由于直线AB上B端点距离正立投影面30mm,根据投影关系作出点B的水平投影b。 3. 根据直线AB长度为15mm,作出点A的水平投影a, 直线AB的正面投影和水平投影参见图 1.7。 图 1.7 习题 4 三角形 ABC 中 AB 为水平线,BC 为正平线,补全三角形 ABC 的投影(参见图 1.8(a))。 解题分析:本题主要利用水平线和正平线的投影特性进行解题。水平线的正面投影平行于X 轴。正平线的水平投影平行于X轴。如若求三角形ABC的投影,只要将三角形的三条边的投影 作出,即可得到三角形ABC的投影。 9

解题步骤: 上电于B为水平线因此其正面投勤心应平行于植。根振拉影关系作出点的正面抄 2.由于BC为正平线,因此其水平投影c应平行于X轴,根据投影关系作出点C的水平投影c。 3.连接a'c',连接ac,三角形ABC的正面投影和水平投影补画完成,参见图1.8(b). b) 图1.8 习题5已知平面为正垂面,=30°,补画出其在另两个投影面上的投影(参见图1.9(a), 并分析有几解。 图19 解题分析:本题主要利用正垂面的投影特性进行解题。正垂面在正立投影面的投影积聚为 条直线,并能反映正垂面与水平投影而的夹角以及正垂面与侧立投影面的夹角。本题目的己
解题步骤: 1. 由于AB为水平线,因此其正面投影a′b′应平行于X轴,根据投影关系作出点A的正面投 影a′。 2. 由于BC为正平线,因此其水平投影bc应平行于X轴,根据投影关系作出点C的水平投影c。 3. 连接 a′c′,连接 ac,三角形 ABC 的正面投影和水平投影补画完成,参见图 1.8(b)。 (a) (b) 图 1.8 习题 5 已知平面为正垂面,α=30°,补画出其在另两个投影面上的投影(参见图 1.9(a)), 并分析有几解。 (a) (b) 图 1.9 解题分析:本题主要利用正垂面的投影特性进行解题。正垂面在正立投影面的投影积聚为一 条直线,并能反映正垂面与水平投影面的夹角以及正垂面与侧立投影面的夹角。本题目的已 10