
5 微生物反应器操作 教学基本内容: 讲授微生物反应器的操作方式,包括分批式操作、连续式操作、流加式操作。连续 式操作的定义、数学模型,连续稳态操作条件,连续操作的优缺点,在生产上和科研中 的应用;流加式操作的定义、数学模型,定流量流加、指数流加的概念,流加式操作的 控制优化问题。分批式操作下微生物生长曲线。 5.1 微生物反应器操作基础 5.2 连续式操作 5.3 流加式操作 5.4 分批式操作 授课重点: 1. 三种基本操作方式的比较。 2. 单级连续式操作的数学模型,连续稳态操作条件,冲出现象。 3. 连续操作的优缺点及在生产上和科研领域的应用。 4 流加式操作的数学模型,指数流加和定流量流加的概念。 5. 流加操作的控制与优化。 6. 分批式操作下微生物的生长曲线。 难点: 1. 连续式操作的数学模型。 2. 多级连续培养的数学模型。 3. 流加式操作的数学模型。 本章主要教学要求: 1. 理解微生物反应器操作方式的概念。注意连续式操作、流加式操作和分批式操作 的区别。 2. 理解和掌握连续式操作的数学模型及连续稳态操作条件。 3. 理解指数流加和定流量流加的区别。 4. 了解连续式操作的优缺点和应用。 5. 了解流加式操作的优化和控制
5 微生物反应器操作 教学基本内容: 讲授微生物反应器的操作方式,包括分批式操作、连续式操作、流加式操作。连续 式操作的定义、数学模型,连续稳态操作条件,连续操作的优缺点,在生产上和科研中 的应用;流加式操作的定义、数学模型,定流量流加、指数流加的概念,流加式操作的 控制优化问题。分批式操作下微生物生长曲线。 5.1 微生物反应器操作基础 5.2 连续式操作 5.3 流加式操作 5.4 分批式操作 授课重点: 1. 三种基本操作方式的比较。 2. 单级连续式操作的数学模型,连续稳态操作条件,冲出现象。 3. 连续操作的优缺点及在生产上和科研领域的应用。 4 流加式操作的数学模型,指数流加和定流量流加的概念。 5. 流加操作的控制与优化。 6. 分批式操作下微生物的生长曲线。 难点: 1. 连续式操作的数学模型。 2. 多级连续培养的数学模型。 3. 流加式操作的数学模型。 本章主要教学要求: 1. 理解微生物反应器操作方式的概念。注意连续式操作、流加式操作和分批式操作 的区别。 2. 理解和掌握连续式操作的数学模型及连续稳态操作条件。 3. 理解指数流加和定流量流加的区别。 4. 了解连续式操作的优缺点和应用。 5. 了解流加式操作的优化和控制
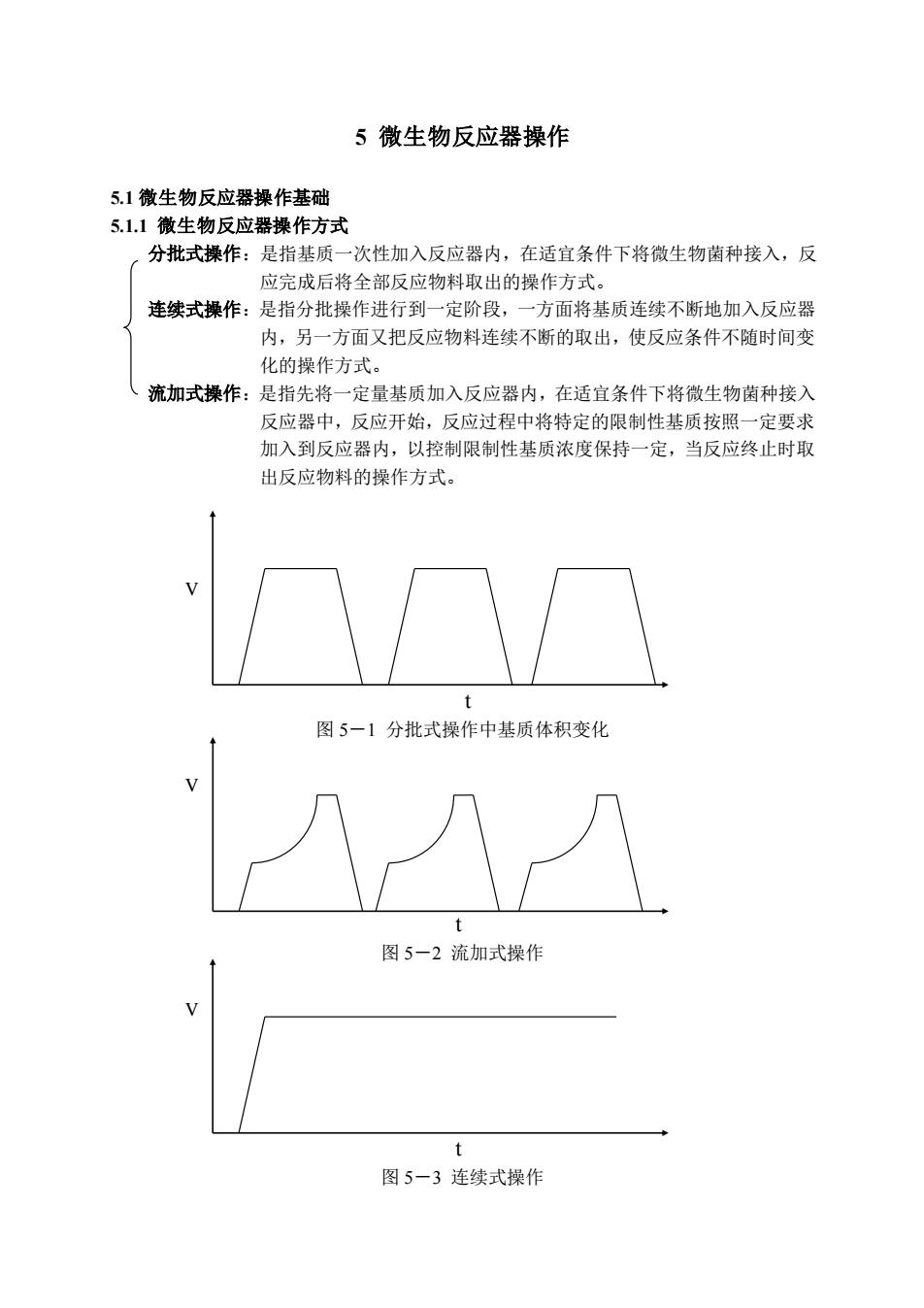
5 微生物反应器操作 5.1 微生物反应器操作基础 5.1.1 微生物反应器操作方式 分批式操作:是指基质一次性加入反应器内,在适宜条件下将微生物菌种接入,反 应完成后将全部反应物料取出的操作方式。 连续式操作:是指分批操作进行到一定阶段,一方面将基质连续不断地加入反应器 内,另一方面又把反应物料连续不断的取出,使反应条件不随时间变 化的操作方式。 流加式操作:是指先将一定量基质加入反应器内,在适宜条件下将微生物菌种接入 反应器中,反应开始,反应过程中将特定的限制性基质按照一定要求 加入到反应器内,以控制限制性基质浓度保持一定,当反应终止时取 出反应物料的操作方式。 V t 图 5-1 分批式操作中基质体积变化 V t 图 5-2 流加式操作 V t 图 5-3 连续式操作
5 微生物反应器操作 5.1 微生物反应器操作基础 5.1.1 微生物反应器操作方式 分批式操作:是指基质一次性加入反应器内,在适宜条件下将微生物菌种接入,反 应完成后将全部反应物料取出的操作方式。 连续式操作:是指分批操作进行到一定阶段,一方面将基质连续不断地加入反应器 内,另一方面又把反应物料连续不断的取出,使反应条件不随时间变 化的操作方式。 流加式操作:是指先将一定量基质加入反应器内,在适宜条件下将微生物菌种接入 反应器中,反应开始,反应过程中将特定的限制性基质按照一定要求 加入到反应器内,以控制限制性基质浓度保持一定,当反应终止时取 出反应物料的操作方式。 V t 图 5-1 分批式操作中基质体积变化 V t 图 5-2 流加式操作 V t 图 5-3 连续式操作

5.1.2 不同操作方式的特点 在分批式操作中,反应液中基质浓度 S 随反应进行不断降低,菌体浓度 X、产物浓 度 P 则不断升高,因此是一个动态变化过程。当微生物反应存在底物抑制时,初期底物 浓度高不利于反应。后期底物浓度过低,则反应速度很低。 在流加式操作中,基质浓度控制在一定水平,避免了底物抑制问题。流加过程中反 应液体积是变化的。流加式操作可达到拟稳态。 在连续式操作中,反应液体积 V、底物浓度 S、菌体浓度 X、产物浓度 P 保持恒定, 连绵式操作是一个稳态过程。 5.1.3 不同操作方式的优缺点 见教材 73 页表 5-1。 5.2 连续式操作 连续式操作有两大类型,即 CSTR 型和 CPFR 型,CPFR 型多用于酶促反应过程, 微生物反应的连续式操作多采用 CSTR 型。 根据达成稳定状态的方法不同,CSTR 型连续操作,大致可分为以下 3 种: 恒化器法:指连续培养过程中,基质流加速度恒定,以调节微生物细胞的生长速率 与恒定流量相适应的方法。 恒浊器法:指预先规定细胞浓度,通过基质流量控制,以适应细胞的既定浓度的方 法。 营养物恒定法:指通过流加一定成分,使培养基中的营养成分恒定的方法。 5.2.1 恒化器法单级连续操作 5.2.1.1 数学模型 图 5-4 所示的单级 CSTR 培养系统中,流入液中仅一种成分为微生物生长的限制 性因子,其他成分在不发生抑制的条件下充分存在。 图 5-4 单级 CSTR 培养系统 菌体的物料衡算式:变化量 = 流入量+生长量−流出量 F(S0,X0) F(S,X,P) S,X,P
5.1.2 不同操作方式的特点 在分批式操作中,反应液中基质浓度 S 随反应进行不断降低,菌体浓度 X、产物浓 度 P 则不断升高,因此是一个动态变化过程。当微生物反应存在底物抑制时,初期底物 浓度高不利于反应。后期底物浓度过低,则反应速度很低。 在流加式操作中,基质浓度控制在一定水平,避免了底物抑制问题。流加过程中反 应液体积是变化的。流加式操作可达到拟稳态。 在连续式操作中,反应液体积 V、底物浓度 S、菌体浓度 X、产物浓度 P 保持恒定, 连绵式操作是一个稳态过程。 5.1.3 不同操作方式的优缺点 见教材 73 页表 5-1。 5.2 连续式操作 连续式操作有两大类型,即 CSTR 型和 CPFR 型,CPFR 型多用于酶促反应过程, 微生物反应的连续式操作多采用 CSTR 型。 根据达成稳定状态的方法不同,CSTR 型连续操作,大致可分为以下 3 种: 恒化器法:指连续培养过程中,基质流加速度恒定,以调节微生物细胞的生长速率 与恒定流量相适应的方法。 恒浊器法:指预先规定细胞浓度,通过基质流量控制,以适应细胞的既定浓度的方 法。 营养物恒定法:指通过流加一定成分,使培养基中的营养成分恒定的方法。 5.2.1 恒化器法单级连续操作 5.2.1.1 数学模型 图 5-4 所示的单级 CSTR 培养系统中,流入液中仅一种成分为微生物生长的限制 性因子,其他成分在不发生抑制的条件下充分存在。 图 5-4 单级 CSTR 培养系统 菌体的物料衡算式:变化量 = 流入量+生长量−流出量 F(S0,X0) F(S,X,P) S,X,P

即: V X FV dt dX V = − (5-1) 限制性基质的物料衡算式:变化量=流入量−流出量-消耗量 即 FS S V X dt dS V in out = − − (5-2) 产物的物料衡算式:变化量=流入量+生成量−流出量 即: V X FP dt dP V = − (5-3) (5-1)式~(5-3)式两边同除以 V,则 D X dt dX = ( − ) (5-4) D S S X dt dS in out = ( − ) − (5-5) X DP dt dP = − (5-6) 式中 D 为稀释率, V F D = 稳定状态下, = = = 0 dt dP dt dS dt dX ,因此 D=μ (5-7) ( ) X = YX / S Sin − Sout (5-8) ( ) P = YP / S Sin − Sout (5-9) 若微生物生长符合莫诺模型,则 D K D S S out − = max (5-10) (5-7)式~(5-10)式为恒化器法单级连续培养的数学模型。稀释率 D 是一个 重要的操作参数。根据上述方程可知当 D 确定时,、S、X、P 即可唯一确定。D=F/V, 因此,当反应液体积一定时,可通过控制流量 F 来控制、S、X、P,这正是恒化器法 又被称为外部控制方法的缘故。 5.2.1.2 连续稳态操作条件: D 的取值是有限制的,即应有 S in in crit K S S D D + = max , 式中, Dcrit 为临界稀释率。 微生物反应一般是在 Sin KS 条件下进行的,所以 Dcrit max 当 D Dcrit 时,根据(5-4)式可知,反应器中菌体终将全部被冲出(wash-out),称
即: V X FV dt dX V = − (5-1) 限制性基质的物料衡算式:变化量=流入量−流出量-消耗量 即 FS S V X dt dS V in out = − − (5-2) 产物的物料衡算式:变化量=流入量+生成量−流出量 即: V X FP dt dP V = − (5-3) (5-1)式~(5-3)式两边同除以 V,则 D X dt dX = ( − ) (5-4) D S S X dt dS in out = ( − ) − (5-5) X DP dt dP = − (5-6) 式中 D 为稀释率, V F D = 稳定状态下, = = = 0 dt dP dt dS dt dX ,因此 D=μ (5-7) ( ) X = YX / S Sin − Sout (5-8) ( ) P = YP / S Sin − Sout (5-9) 若微生物生长符合莫诺模型,则 D K D S S out − = max (5-10) (5-7)式~(5-10)式为恒化器法单级连续培养的数学模型。稀释率 D 是一个 重要的操作参数。根据上述方程可知当 D 确定时,、S、X、P 即可唯一确定。D=F/V, 因此,当反应液体积一定时,可通过控制流量 F 来控制、S、X、P,这正是恒化器法 又被称为外部控制方法的缘故。 5.2.1.2 连续稳态操作条件: D 的取值是有限制的,即应有 S in in crit K S S D D + = max , 式中, Dcrit 为临界稀释率。 微生物反应一般是在 Sin KS 条件下进行的,所以 Dcrit max 当 D Dcrit 时,根据(5-4)式可知,反应器中菌体终将全部被冲出(wash-out),称

为冲出现象。 5.2.1.3 菌体产率、产物产率 菌体产率 − = = − D K D P DX Y D S S X X S in max / (5-11) 产物产率 − = = − D K D P DP Y D S S P P S in max / (5-12) 获得最大菌体产率(或最大产物产率)时的稀释率为 + = − S in S K S K Dmax max 1 (5-13) 此时,最大菌体产率为 ( ) 2 max / max max max max max / ( ) X S in S S S X S in Y S K K D K D DX D Y S = + − − = − (5-14) 最高产物产率为 ( ) 2 max / max max max max max / ( ) P S in S S S P S in Y S K K D K D DP D Y S = + − − = − (5-15) 当 KS Sin 时, DX max maxYX / S Sin ( ) = , DP max maxYP/ S Sin ( ) = (5-16) 例 1:以葡萄糖为限制性底物,连续培养大肠杆菌,在此培养条件下,测得实验数据如 下,比较理论与实验的结果。已知m=1.08h-1,KS=0.102g/L,YX/S=0.505g/g。 单级恒化器连续培养大肠杆菌 S0=0.968g/L 稀释率 D(h-1 ) 葡萄糖 S(mg/L) 菌体浓度 X(mg/L) 菌体产率 DX(mg/L.h) 0.06 6 427 26 0.12 13 434 52 0.24 33 417 100 0.31 40 438 136 0.43 64 422 181 0.53 102 427 226 0.60 122 424 254 0.66 153 422 279 0.69 170 430 297 0.71 221 390 277 0.73 210 352 257
为冲出现象。 5.2.1.3 菌体产率、产物产率 菌体产率 − = = − D K D P DX Y D S S X X S in max / (5-11) 产物产率 − = = − D K D P DP Y D S S P P S in max / (5-12) 获得最大菌体产率(或最大产物产率)时的稀释率为 + = − S in S K S K Dmax max 1 (5-13) 此时,最大菌体产率为 ( ) 2 max / max max max max max / ( ) X S in S S S X S in Y S K K D K D DX D Y S = + − − = − (5-14) 最高产物产率为 ( ) 2 max / max max max max max / ( ) P S in S S S P S in Y S K K D K D DP D Y S = + − − = − (5-15) 当 KS Sin 时, DX max maxYX / S Sin ( ) = , DP max maxYP/ S Sin ( ) = (5-16) 例 1:以葡萄糖为限制性底物,连续培养大肠杆菌,在此培养条件下,测得实验数据如 下,比较理论与实验的结果。已知m=1.08h-1,KS=0.102g/L,YX/S=0.505g/g。 单级恒化器连续培养大肠杆菌 S0=0.968g/L 稀释率 D(h-1 ) 葡萄糖 S(mg/L) 菌体浓度 X(mg/L) 菌体产率 DX(mg/L.h) 0.06 6 427 26 0.12 13 434 52 0.24 33 417 100 0.31 40 438 136 0.43 64 422 181 0.53 102 427 226 0.60 122 424 254 0.66 153 422 279 0.69 170 430 297 0.71 221 390 277 0.73 210 352 257
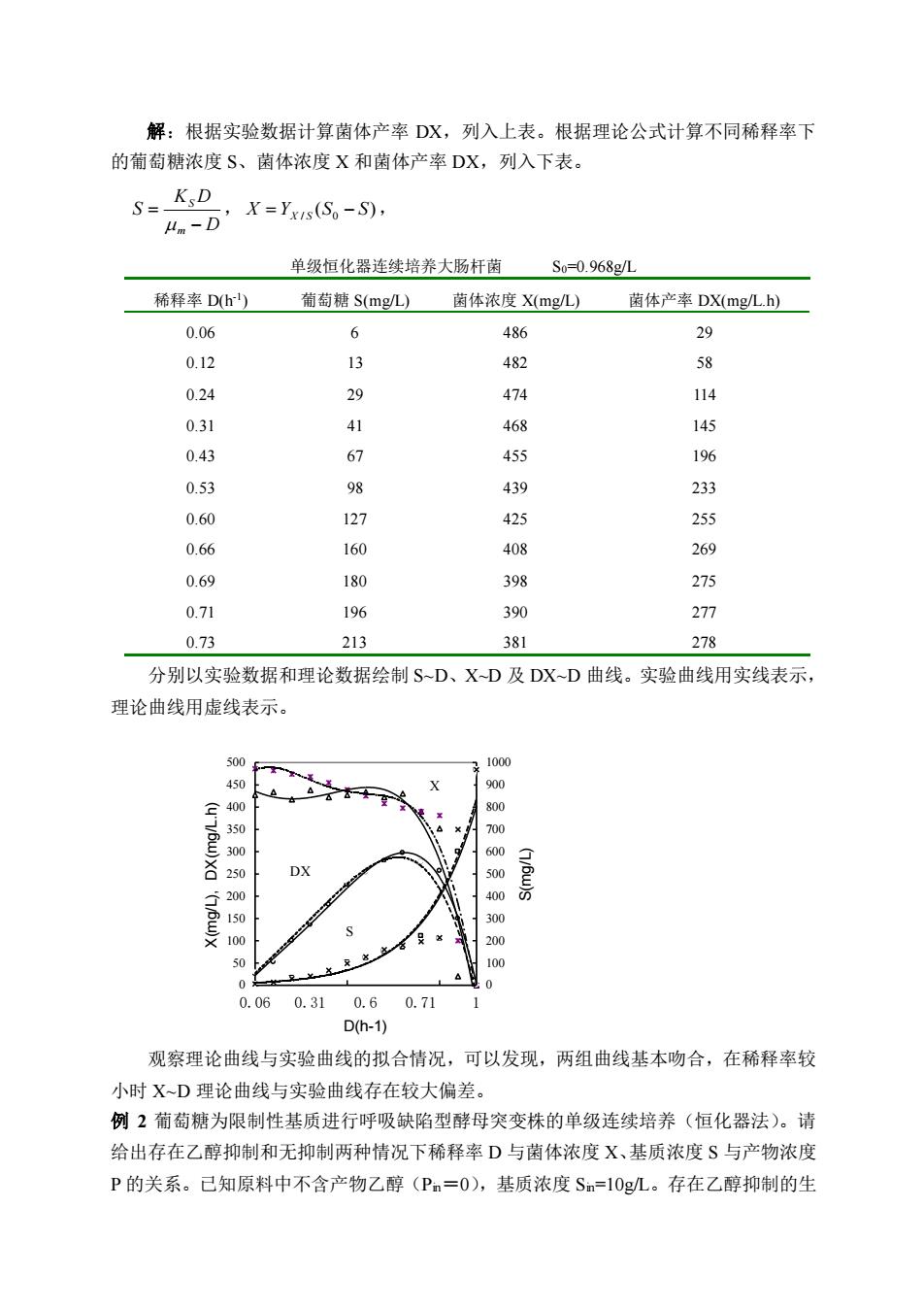
解:根据实验数据计算菌体产率 DX,列入上表。根据理论公式计算不同稀释率下 的葡萄糖浓度 S、菌体浓度 X 和菌体产率 DX,列入下表。 D K D S m S − = , ( ) X = YX / S S0 − S , 单级恒化器连续培养大肠杆菌 S0=0.968g/L 稀释率 D(h-1 ) 葡萄糖 S(mg/L) 菌体浓度 X(mg/L) 菌体产率 DX(mg/L.h) 0.06 6 486 29 0.12 13 482 58 0.24 29 474 114 0.31 41 468 145 0.43 67 455 196 0.53 98 439 233 0.60 127 425 255 0.66 160 408 269 0.69 180 398 275 0.71 196 390 277 0.73 213 381 278 分别以实验数据和理论数据绘制 S~D、X~D 及 DX~D 曲线。实验曲线用实线表示, 理论曲线用虚线表示。 观察理论曲线与实验曲线的拟合情况,可以发现,两组曲线基本吻合,在稀释率较 小时 X~D 理论曲线与实验曲线存在较大偏差。 例 2 葡萄糖为限制性基质进行呼吸缺陷型酵母突变株的单级连续培养(恒化器法)。请 给出存在乙醇抑制和无抑制两种情况下稀释率 D 与菌体浓度 X、基质浓度 S 与产物浓度 P 的关系。已知原料中不含产物乙醇(Pin=0),基质浓度 Sin=10g/L。存在乙醇抑制的生 0 50 100 150 200 250 300 350 400 450 500 0.06 0.31 0.6 0.71 1 D(h-1) X(mg/L), DX(mg/L.h) 0 100 200 300 400 500 600 700 800 900 1000 S(mg/L) X DX S
解:根据实验数据计算菌体产率 DX,列入上表。根据理论公式计算不同稀释率下 的葡萄糖浓度 S、菌体浓度 X 和菌体产率 DX,列入下表。 D K D S m S − = , ( ) X = YX / S S0 − S , 单级恒化器连续培养大肠杆菌 S0=0.968g/L 稀释率 D(h-1 ) 葡萄糖 S(mg/L) 菌体浓度 X(mg/L) 菌体产率 DX(mg/L.h) 0.06 6 486 29 0.12 13 482 58 0.24 29 474 114 0.31 41 468 145 0.43 67 455 196 0.53 98 439 233 0.60 127 425 255 0.66 160 408 269 0.69 180 398 275 0.71 196 390 277 0.73 213 381 278 分别以实验数据和理论数据绘制 S~D、X~D 及 DX~D 曲线。实验曲线用实线表示, 理论曲线用虚线表示。 观察理论曲线与实验曲线的拟合情况,可以发现,两组曲线基本吻合,在稀释率较 小时 X~D 理论曲线与实验曲线存在较大偏差。 例 2 葡萄糖为限制性基质进行呼吸缺陷型酵母突变株的单级连续培养(恒化器法)。请 给出存在乙醇抑制和无抑制两种情况下稀释率 D 与菌体浓度 X、基质浓度 S 与产物浓度 P 的关系。已知原料中不含产物乙醇(Pin=0),基质浓度 Sin=10g/L。存在乙醇抑制的生 0 50 100 150 200 250 300 350 400 450 500 0.06 0.31 0.6 0.71 1 D(h-1) X(mg/L), DX(mg/L.h) 0 100 200 300 400 500 600 700 800 900 1000 S(mg/L) X DX S

长动力学模型可采用 K P K K S S P P S + + = max 解:存在乙醇抑制时, K P K K S S P P S out out + + = max 连续培养稳态下, D = D K P K K D S P P S out − + = max − + = − = − D K P K K D X Y S S Y S P P S X S in out X S in max / / ( ) − + = − = − D K P K K D P Y S S Y S P P S P S in out P S in max / / ( ) 无乙醇抑制时, S out out K S S + = max 连续培养稳态下, D = D K D S S out − = max ( ) max / D K D X Y S S X S in − = − ( ) max / D K D P Y S S P S in − = − 例 3 判断题 1) 单罐连续培养稳态下,稀释率与生长比速的关系: D> ( ) D= ( ) D< ( ) D==0 ( )
长动力学模型可采用 K P K K S S P P S + + = max 解:存在乙醇抑制时, K P K K S S P P S out out + + = max 连续培养稳态下, D = D K P K K D S P P S out − + = max − + = − = − D K P K K D X Y S S Y S P P S X S in out X S in max / / ( ) − + = − = − D K P K K D P Y S S Y S P P S P S in out P S in max / / ( ) 无乙醇抑制时, S out out K S S + = max 连续培养稳态下, D = D K D S S out − = max ( ) max / D K D X Y S S X S in − = − ( ) max / D K D P Y S S P S in − = − 例 3 判断题 1) 单罐连续培养稳态下,稀释率与生长比速的关系: D> ( ) D= ( ) D< ( ) D==0 ( )

3) 单罐连续培养稳态下,在洗出稀释率下,可达到最大的菌体产率。() 4) 单罐连续培养稳态下,在 Dmax 的细胞浓度不是最大细胞浓度。() 5) 单罐连续培养稳态下,细胞浓度越高,菌体产率越大。() 6) 单罐连续培养稳态下,在洗出稀释率下罐内底物浓度等于零。() 7) 单罐连续培养稳态下,细胞浓度越高,罐内底物浓度越低。() 例 4(教材例 4-7)求青霉素连续发酵的稳定状态下最大菌体生成速度(DX)max 及此时的 稀释率 Dmax,菌体浓度 X 和基质浓度 Sout。已知 Sin=30g/L,YX/S=0.45,菌体生长可用 Monod 方程表达,max=0.18h -1,KS=1.0g/L。 解:菌体生长符合 Monod 模型,连续培养稳态下达到最大菌体生成速度的稀释率 0.15( ) 1.0 30 1.0 1 0.18 1 1 max max − = + = − + = − h K S K D S in S 5( / ) 0.18 0.15 1.0 0.15 max max max g L D K D S S out = − = − = ( ) 0.45 (30 5) 11.25( / ) X = YX / S Sin − Sout = − = g L (DX )max = DmaxX max = 0.1511.25 =1.69[g /(L h)] 5.2.2 具有反馈的单级连续培养 有时为了增加反应器内的菌体浓度,或者在某种条件下提高发酵产物的产率,对单 级连续培养可以采取将反应器排出液中的部分菌体重新返回反应器中。 5.2.2.1 数学模型 图 5-5 具有反馈的单级连续培养 图 5-5 表示具有反馈的单级连续培养系统,图中 g 为微生物的浓缩系数(g1),r 为再循环反应液的比例(返回的反应液与供给的新鲜反应液的体积比)。 菌体衡算式: F(S0) (1+)F(X,S) S, X F{[1+(1-)]X,S} F(X,S)
3) 单罐连续培养稳态下,在洗出稀释率下,可达到最大的菌体产率。() 4) 单罐连续培养稳态下,在 Dmax 的细胞浓度不是最大细胞浓度。() 5) 单罐连续培养稳态下,细胞浓度越高,菌体产率越大。() 6) 单罐连续培养稳态下,在洗出稀释率下罐内底物浓度等于零。() 7) 单罐连续培养稳态下,细胞浓度越高,罐内底物浓度越低。() 例 4(教材例 4-7)求青霉素连续发酵的稳定状态下最大菌体生成速度(DX)max 及此时的 稀释率 Dmax,菌体浓度 X 和基质浓度 Sout。已知 Sin=30g/L,YX/S=0.45,菌体生长可用 Monod 方程表达,max=0.18h -1,KS=1.0g/L。 解:菌体生长符合 Monod 模型,连续培养稳态下达到最大菌体生成速度的稀释率 0.15( ) 1.0 30 1.0 1 0.18 1 1 max max − = + = − + = − h K S K D S in S 5( / ) 0.18 0.15 1.0 0.15 max max max g L D K D S S out = − = − = ( ) 0.45 (30 5) 11.25( / ) X = YX / S Sin − Sout = − = g L (DX )max = DmaxX max = 0.1511.25 =1.69[g /(L h)] 5.2.2 具有反馈的单级连续培养 有时为了增加反应器内的菌体浓度,或者在某种条件下提高发酵产物的产率,对单 级连续培养可以采取将反应器排出液中的部分菌体重新返回反应器中。 5.2.2.1 数学模型 图 5-5 具有反馈的单级连续培养 图 5-5 表示具有反馈的单级连续培养系统,图中 g 为微生物的浓缩系数(g1),r 为再循环反应液的比例(返回的反应液与供给的新鲜反应液的体积比)。 菌体衡算式: F(S0) (1+)F(X,S) S, X F{[1+(1-)]X,S} F(X,S)

FrgX F r X V X dt dX V = − (1+ ) + (5-17) 基质衡算式: FS F r S FrS V X dt dS V in = − (1+ ) + − (5-18) 培养达到稳定状态时, = = 0 dt dS dt dX 即: =D(1+r-gr)=DR (5-19) ( ) ( ) ( ) / 0 in out X S in out S S R Y S S R S S D X − = − − = = (5-20) 式中,R 为循环浓缩因子,R=1+r-rg,0 R 1 若微生物生长模型可采用 Monod 方程,则 DR K K DR S S S − = − = max max (5-21) (5-19)式、(5-20)式、(5-21)式为具有反馈的单级连续培养数学模型。 5.2.2.2 稳态操作条件: K S R S R D S crit max 0 1 max 0 = + = (在通常情况下,Sin<<KS) (5-22) 稳态操作条件:D Dcrit 可见,具有反馈的单级恒化器与无反馈的单级恒化器相比,稳定状态下的菌体浓度 X 增大,临界稀释率增大。 5.2.2.3 菌体产率 对具有反馈的单级连续培养,还应考虑排出反应液中的菌体浓度 X。 菌体分离装置处的菌体衡算式为 F(1+ r)X = FX + FrgX (5-23) 所以,从分离装置处流出的菌体浓度 X = (1+ r − gr)X = RX (5-24) 菌体产率 RX X R DX = = (5-25) 例 5(教材例 4-9)以葡萄糖为基质在如下条件进行具有反馈的连续操作。V=1m3;F =0.1m3 /h;YX/S=0.158g/g(以细胞/葡萄糖计);Sin=10kg/m3;r=0.8;g=1.5。已知微生物 反应可以用 Monod 方程来表示,其中max=0.41h-1,KS=0.22kg/m3,求比生长速率,反 应器内基质浓度 Sout 和菌体浓度 X 和分离装置出口处的菌体浓度 X
FrgX F r X V X dt dX V = − (1+ ) + (5-17) 基质衡算式: FS F r S FrS V X dt dS V in = − (1+ ) + − (5-18) 培养达到稳定状态时, = = 0 dt dS dt dX 即: =D(1+r-gr)=DR (5-19) ( ) ( ) ( ) / 0 in out X S in out S S R Y S S R S S D X − = − − = = (5-20) 式中,R 为循环浓缩因子,R=1+r-rg,0 R 1 若微生物生长模型可采用 Monod 方程,则 DR K K DR S S S − = − = max max (5-21) (5-19)式、(5-20)式、(5-21)式为具有反馈的单级连续培养数学模型。 5.2.2.2 稳态操作条件: K S R S R D S crit max 0 1 max 0 = + = (在通常情况下,Sin<<KS) (5-22) 稳态操作条件:D Dcrit 可见,具有反馈的单级恒化器与无反馈的单级恒化器相比,稳定状态下的菌体浓度 X 增大,临界稀释率增大。 5.2.2.3 菌体产率 对具有反馈的单级连续培养,还应考虑排出反应液中的菌体浓度 X。 菌体分离装置处的菌体衡算式为 F(1+ r)X = FX + FrgX (5-23) 所以,从分离装置处流出的菌体浓度 X = (1+ r − gr)X = RX (5-24) 菌体产率 RX X R DX = = (5-25) 例 5(教材例 4-9)以葡萄糖为基质在如下条件进行具有反馈的连续操作。V=1m3;F =0.1m3 /h;YX/S=0.158g/g(以细胞/葡萄糖计);Sin=10kg/m3;r=0.8;g=1.5。已知微生物 反应可以用 Monod 方程来表示,其中max=0.41h-1,KS=0.22kg/m3,求比生长速率,反 应器内基质浓度 Sout 和菌体浓度 X 和分离装置出口处的菌体浓度 X

解:微生物反应可以用 Monod 方程来表示,具有反馈的连续培养稳态下, 0.1( ) 1 0.1 −1 = = = = h V F D R = 1+ r − rg = 1+ 0.8 − 0.81.5 = 0.6 0.038( / ) 0.41 0.1 0.6 0.22 0.1 0.6 3 max max max k g m DR K DR DR K K DR S S S S out = − = − = − = − = (10 0.038) 2.62( / ) 0.6 0.158 ( ) / 3 S S k g m R Y X in out X S = − = − = (1 ) 0.6 2.62 1.57( / ) 3 X = + r − gr X = RX = = k g m 5.2.3 多级连续培养 5.2.3.1 数学模型:以微生物生长符合莫诺模型为例。 图 5-6 多级连续培养 操作达到稳态时,第一级罐 1 = D (5-26) ( ) X1 = YX / S S0 − S1 (5-27) ( ) P1 = YP / S S0 − S1 (5-28) D K D S S − = max 1 (5-29) 第 n 级罐物料衡算式 = n−1 − n + n n = 0 n FX FX V X dt dX V (5-30) = n−1 − n − n n = 0 n FS FS V X dt dS V (5-31) = n−1 − n + n n = 0 n FP FP V X dt dP V (5-32) F,S1,X1,P1 F,S2,X2,P2 F,S3,X3,P3 F,So
解:微生物反应可以用 Monod 方程来表示,具有反馈的连续培养稳态下, 0.1( ) 1 0.1 −1 = = = = h V F D R = 1+ r − rg = 1+ 0.8 − 0.81.5 = 0.6 0.038( / ) 0.41 0.1 0.6 0.22 0.1 0.6 3 max max max k g m DR K DR DR K K DR S S S S out = − = − = − = − = (10 0.038) 2.62( / ) 0.6 0.158 ( ) / 3 S S k g m R Y X in out X S = − = − = (1 ) 0.6 2.62 1.57( / ) 3 X = + r − gr X = RX = = k g m 5.2.3 多级连续培养 5.2.3.1 数学模型:以微生物生长符合莫诺模型为例。 图 5-6 多级连续培养 操作达到稳态时,第一级罐 1 = D (5-26) ( ) X1 = YX / S S0 − S1 (5-27) ( ) P1 = YP / S S0 − S1 (5-28) D K D S S − = max 1 (5-29) 第 n 级罐物料衡算式 = n−1 − n + n n = 0 n FX FX V X dt dX V (5-30) = n−1 − n − n n = 0 n FS FS V X dt dS V (5-31) = n−1 − n + n n = 0 n FP FP V X dt dP V (5-32) F,S1,X1,P1 F,S2,X2,P2 F,S3,X3,P3 F,So