
4 微生物反应动力学 教学基本内容: 微生物反应的特点;微生物反应的质量衡算,包括碳素衡算、碳源衡算、 氧衡算;微生物反应的能量衡算。微生物反应动力学,包括生长动力学、基质消 耗动力学和产物生成动力学 4.1 微生物反应的特点 4.2 微生物反应过程的质量与能量衡算 4.2.1 碳素衡算 4.2.2 碳源衡算 4.2.3 氧衡算 4.2.3 能量衡算 4.3 微生物反应动力学 4.3.1 生长动力学 4.3.2 基质消耗动力学 4.3.3 产物生成动力学 授课重点: 1. 微生物反应与酶促反应的比较。 2. 微生物反应式及微生物反应平衡式的概念。 3. 菌体实验化学式的概念与测定方法。 4. 微生物反应中的动力学变量。 5. 微生物反应的得率系数的概念。 6. 微生物反应的维持常数的概念。 7. 碳素衡算。 8. 碳源衡算。 9. 氧衡算。 10. 能量衡算。 11. 莫诺方程。 12. 产物的 Gaden 模型。 难点: 1. 微生物反应涉及到的动力学变量和参数远多于酶促反应。 2.微生物反应过程中碳源衡算、氧衡算和能量衡算间的关系
4 微生物反应动力学 教学基本内容: 微生物反应的特点;微生物反应的质量衡算,包括碳素衡算、碳源衡算、 氧衡算;微生物反应的能量衡算。微生物反应动力学,包括生长动力学、基质消 耗动力学和产物生成动力学 4.1 微生物反应的特点 4.2 微生物反应过程的质量与能量衡算 4.2.1 碳素衡算 4.2.2 碳源衡算 4.2.3 氧衡算 4.2.3 能量衡算 4.3 微生物反应动力学 4.3.1 生长动力学 4.3.2 基质消耗动力学 4.3.3 产物生成动力学 授课重点: 1. 微生物反应与酶促反应的比较。 2. 微生物反应式及微生物反应平衡式的概念。 3. 菌体实验化学式的概念与测定方法。 4. 微生物反应中的动力学变量。 5. 微生物反应的得率系数的概念。 6. 微生物反应的维持常数的概念。 7. 碳素衡算。 8. 碳源衡算。 9. 氧衡算。 10. 能量衡算。 11. 莫诺方程。 12. 产物的 Gaden 模型。 难点: 1. 微生物反应涉及到的动力学变量和参数远多于酶促反应。 2.微生物反应过程中碳源衡算、氧衡算和能量衡算间的关系

3. 自由能消耗对菌体得率 YKJ 的计算。 本章主要教学要求: 1. 理解微生物反应与酶促反应的区别。 2. 掌握菌体实验化学式的测定方法。 3. 掌握微生物反应式中系数的确定方法。 4. 掌握微生物反应中动力学变量及参数的数学定义。 5. 理解碳素衡算式。 6. 理解碳源衡算式。 7 理解氧衡算式。 8. 理解碳源衡算与氧衡算、能量衡算之间的内在联系。 9. 掌握有效电子转移的概念,掌握 YKJ 的计算方法。 10. 了解生长模型的分类。 11. 理解莫诺方程与米氏方程的区别。掌握莫诺方程中动力学参数的测定方 法。 12. 理解产物的 Gaden 模型
3. 自由能消耗对菌体得率 YKJ 的计算。 本章主要教学要求: 1. 理解微生物反应与酶促反应的区别。 2. 掌握菌体实验化学式的测定方法。 3. 掌握微生物反应式中系数的确定方法。 4. 掌握微生物反应中动力学变量及参数的数学定义。 5. 理解碳素衡算式。 6. 理解碳源衡算式。 7 理解氧衡算式。 8. 理解碳源衡算与氧衡算、能量衡算之间的内在联系。 9. 掌握有效电子转移的概念,掌握 YKJ 的计算方法。 10. 了解生长模型的分类。 11. 理解莫诺方程与米氏方程的区别。掌握莫诺方程中动力学参数的测定方 法。 12. 理解产物的 Gaden 模型

4 微生物反应动力学 19 世纪生物学家巴斯德坚持由糖变为酒精的发酵过程是由细胞产生的,而 毕希纳却发现磨碎了的酵母仍能使糖发酵产生酒精,认为发酵是由活细胞产生的 非生命物质引起的,称为酶。 可见微生物反应与酶促反应在催化作用的实质看是一致的。区别在于微生物 反应过程是自催化过程,生物反应过程中出现菌体增殖;酶促反应过程中,酶只 可能失活,不可能增多。 4.1 微生物反应的质量能量衡算 4.1.1 微生物反应式 在微生物细胞中,包含的酶促反应成百上千,产物是否也是这样多呢?并非 如此。这是由于一个反应的产物,又是另一个反应的基质,这样就形成了一条条 代谢途径,如糖类代谢、脂类代谢、蛋白质代谢。由于存在精巧的代谢调控,如 正反馈、副反馈,中间产物不会大量积累,最终大量积累的只是少数几种终产物。 可见,我们不仅没有可能一个一个研究微生物细胞中的酶反应,也没这个必要。 我们可采用黑箱的研究方法,只考虑其与外界环境的物质交换。因此,微生物反 应过程可以用微生物反应式表示: 碳源 + 氮源 + O2 菌体 + CO2 + H2O + 产物 与普通化学反应及酶促反应不同的是,在微生物反应式中,出现了菌体项。 菌体可以用实验化学式来表示。我们来看微生物细胞的化学成分(见教材 P49 表 3-2)。在微生物细胞中,C、H、O、N 四种元素含量占菌体干重的 90%左右, 因此可用实验化学式表示:CαHβNγOδ,通常令=1。 例 1:细菌的化学元素测定结果是:碳元素含量(干重)53%,氢元素 7.3%,氮元 素 12.0%,氧元素 19.%,确定其化学式。 解:α = 1 1.65 12 53 1 7.3 = = 0.2 12 53 14 12.0 = = 0.27 12 53 16 19.0 = =
4 微生物反应动力学 19 世纪生物学家巴斯德坚持由糖变为酒精的发酵过程是由细胞产生的,而 毕希纳却发现磨碎了的酵母仍能使糖发酵产生酒精,认为发酵是由活细胞产生的 非生命物质引起的,称为酶。 可见微生物反应与酶促反应在催化作用的实质看是一致的。区别在于微生物 反应过程是自催化过程,生物反应过程中出现菌体增殖;酶促反应过程中,酶只 可能失活,不可能增多。 4.1 微生物反应的质量能量衡算 4.1.1 微生物反应式 在微生物细胞中,包含的酶促反应成百上千,产物是否也是这样多呢?并非 如此。这是由于一个反应的产物,又是另一个反应的基质,这样就形成了一条条 代谢途径,如糖类代谢、脂类代谢、蛋白质代谢。由于存在精巧的代谢调控,如 正反馈、副反馈,中间产物不会大量积累,最终大量积累的只是少数几种终产物。 可见,我们不仅没有可能一个一个研究微生物细胞中的酶反应,也没这个必要。 我们可采用黑箱的研究方法,只考虑其与外界环境的物质交换。因此,微生物反 应过程可以用微生物反应式表示: 碳源 + 氮源 + O2 菌体 + CO2 + H2O + 产物 与普通化学反应及酶促反应不同的是,在微生物反应式中,出现了菌体项。 菌体可以用实验化学式来表示。我们来看微生物细胞的化学成分(见教材 P49 表 3-2)。在微生物细胞中,C、H、O、N 四种元素含量占菌体干重的 90%左右, 因此可用实验化学式表示:CαHβNγOδ,通常令=1。 例 1:细菌的化学元素测定结果是:碳元素含量(干重)53%,氢元素 7.3%,氮元 素 12.0%,氧元素 19.%,确定其化学式。 解:α = 1 1.65 12 53 1 7.3 = = 0.2 12 53 14 12.0 = = 0.27 12 53 16 19.0 = =
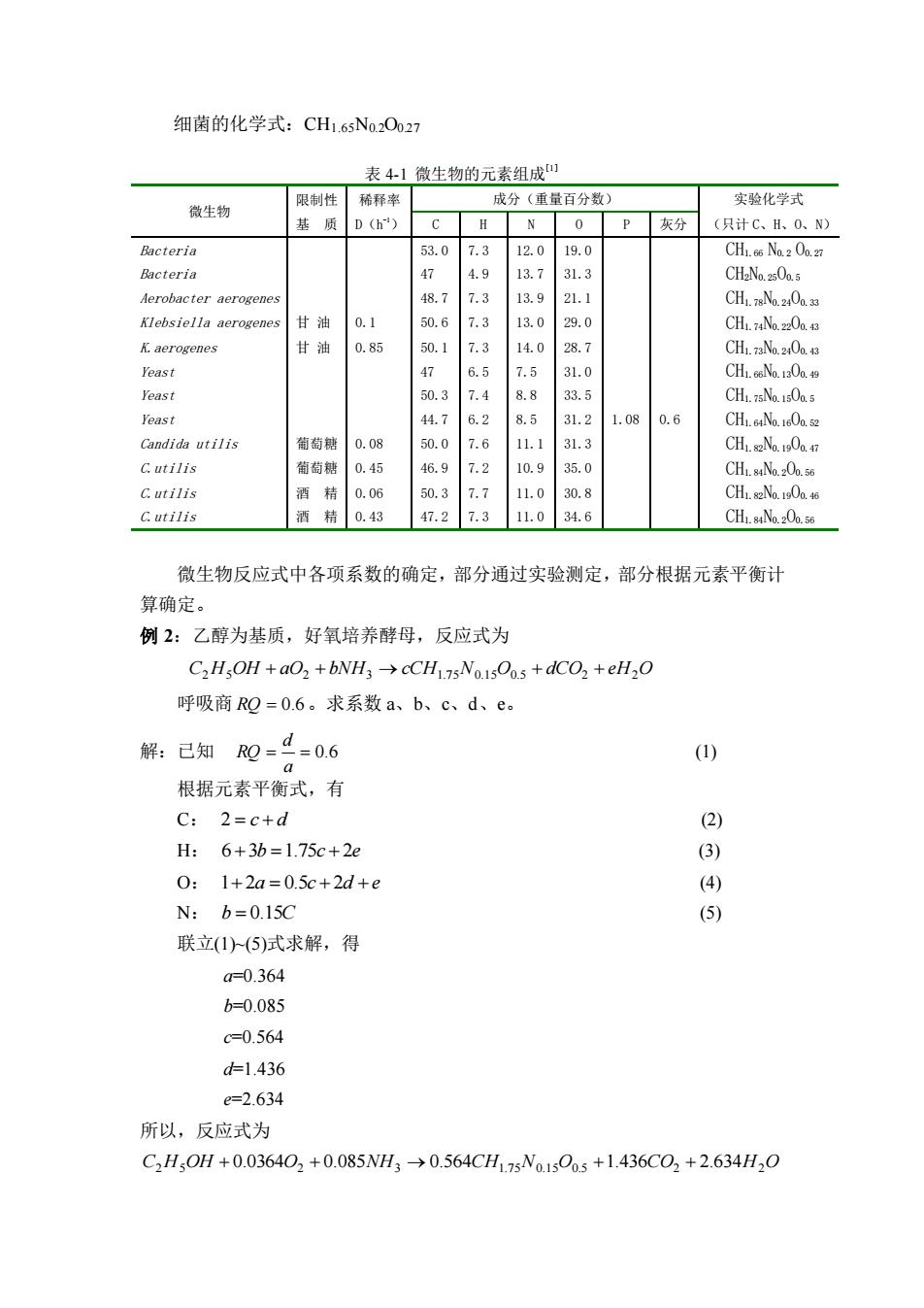
细菌的化学式:CH1.65N0.2O0.27 表 4-1 微生物的元素组成[1] 微生物 限制性 基 质 稀释率 D(h -1) 成分(重量百分数) 实验化学式 C H N O P 灰分 (只计 C、H、O、N) Bacteria 53.0 7.3 12.0 19.0 CH1.66 N0.2 O0.27 Bacteria 47 4.9 13.7 31.3 CH2N0.25O0.5 Aerobacter aerogenes 48.7 7.3 13.9 21.1 CH1.78N0.24O0.33 Klebsiella aerogenes 甘 油 0.1 50.6 7.3 13.0 29.0 CH1.74N0.22O0.43 K.aerogenes 甘 油 0.85 50.1 7.3 14.0 28.7 CH1.73N0.24O0.43 Yeast 47 6.5 7.5 31.0 CH1.66N0.13O0.49 Yeast 50.3 7.4 8.8 33.5 CH1.75N0.15O0.5 Yeast 44.7 6.2 8.5 31.2 1.08 0.6 CH1.64N0.16O0.52 Candida utilis 葡萄糖 0.08 50.0 7.6 11.1 31.3 CH1.82N0.19O0.47 C.utilis 葡萄糖 0.45 46.9 7.2 10.9 35.0 CH1.84N0.2O0.56 C.utilis 酒 精 0.06 50.3 7.7 11.0 30.8 CH1.82N0.19O0.46 C.utilis 酒 精 0.43 47.2 7.3 11.0 34.6 CH1.84N0.2O0.56 微生物反应式中各项系数的确定,部分通过实验测定,部分根据元素平衡计 算确定。 例 2:乙醇为基质,好氧培养酵母,反应式为 C2H5OH + aO2 + bNH3 → cCH1.7 5N0.1 5O0.5 + dCO2 + eH2O 呼吸商 RQ = 0.6 。求系数 a、b、c、d、e。 解:已知 = = 0.6 a d RQ (1) 根据元素平衡式,有 C: 2 = c + d (2) H: 6+3b =1.75c + 2e (3) O: 1+ 2a = 0.5c + 2d + e (4) N: b = 0.15C (5) 联立(1)~(5)式求解,得 a=0.364 b=0.085 c=0.564 d=1.436 e=2.634 所以,反应式为 C2H5OH + 0.0364O2 + 0.085NH3 → 0.564CH1.7 5N0.1 5O0.5 +1.436CO2 + 2.634H2O
细菌的化学式:CH1.65N0.2O0.27 表 4-1 微生物的元素组成[1] 微生物 限制性 基 质 稀释率 D(h -1) 成分(重量百分数) 实验化学式 C H N O P 灰分 (只计 C、H、O、N) Bacteria 53.0 7.3 12.0 19.0 CH1.66 N0.2 O0.27 Bacteria 47 4.9 13.7 31.3 CH2N0.25O0.5 Aerobacter aerogenes 48.7 7.3 13.9 21.1 CH1.78N0.24O0.33 Klebsiella aerogenes 甘 油 0.1 50.6 7.3 13.0 29.0 CH1.74N0.22O0.43 K.aerogenes 甘 油 0.85 50.1 7.3 14.0 28.7 CH1.73N0.24O0.43 Yeast 47 6.5 7.5 31.0 CH1.66N0.13O0.49 Yeast 50.3 7.4 8.8 33.5 CH1.75N0.15O0.5 Yeast 44.7 6.2 8.5 31.2 1.08 0.6 CH1.64N0.16O0.52 Candida utilis 葡萄糖 0.08 50.0 7.6 11.1 31.3 CH1.82N0.19O0.47 C.utilis 葡萄糖 0.45 46.9 7.2 10.9 35.0 CH1.84N0.2O0.56 C.utilis 酒 精 0.06 50.3 7.7 11.0 30.8 CH1.82N0.19O0.46 C.utilis 酒 精 0.43 47.2 7.3 11.0 34.6 CH1.84N0.2O0.56 微生物反应式中各项系数的确定,部分通过实验测定,部分根据元素平衡计 算确定。 例 2:乙醇为基质,好氧培养酵母,反应式为 C2H5OH + aO2 + bNH3 → cCH1.7 5N0.1 5O0.5 + dCO2 + eH2O 呼吸商 RQ = 0.6 。求系数 a、b、c、d、e。 解:已知 = = 0.6 a d RQ (1) 根据元素平衡式,有 C: 2 = c + d (2) H: 6+3b =1.75c + 2e (3) O: 1+ 2a = 0.5c + 2d + e (4) N: b = 0.15C (5) 联立(1)~(5)式求解,得 a=0.364 b=0.085 c=0.564 d=1.436 e=2.634 所以,反应式为 C2H5OH + 0.0364O2 + 0.085NH3 → 0.564CH1.7 5N0.1 5O0.5 +1.436CO2 + 2.634H2O

4.1.2 微生物反应动力学的研究特点 微生物反应动力学研究各种过程变量在活细胞作用下变化的规律,以及各种 反应条件对这些过程变量变化速度的影响。必须注意,微生物反应动力学研究的 对象既然时运动着的物质,就不能单纯地用传统的静态变量如质量、溶氧量、菌 体量等等进行描述,而必须涉及到许多动态变量,如细胞比生长率、基质比消耗 率、CO 比生成率、产物比生产率等等。这些动态变量一般不能直接测量,只能 根据动力学方程式间接估计。 发酵过程的传统控制方法,是凭经验对一些静态变量如 pH、溶氧、残余基 质浓度等按设定点进行孤立控制,它没有系统考虑各变量之间的内在联系,也未 能反映发酵过程的动态特性,因而带有很大的局限性和盲目性。例如,pH 的控 制可用加入酸、碱或者增加培养基中的缓冲成分,或者调节各种基质的补加率来 维持生理酸、碱性物质的代谢平衡的方法在同一水平上实施,但可能出现截然不 同的结果。又如,为了维持某一水平的基质浓度,采用高水平的碳、氮平衡补料 或低水平的碳、氮平衡补料,必然产生大相径庭的结果。还有,以高菌体浓度、 低生长率或低菌体浓度、高生长率达到同一溶氧水平,结果也大不相同。 要对发酵过程进行优化控制,必须了解达到高产所必须具备的生产菌株生长 状态(生长速率、形态、浓度等),相应的基质和氧的需要率,以及各种发酵条 件对这种生长状态和需要量的影响。由于发酵动力学是关于微生物生长率、基质 和氧消耗率、产物合成率等动态变量之间关系以及它们与发酵条件之间关系的学 问,因而掌握这些学问,就能更加系统(而不是孤立)、有效(而不是盲目)的 驾驭这些发酵条件和动态变量,发酵过程的控制问题也就应刃而解了。 按发酵动力学原理对发酵过程进行优化控制,涉及到许许多多数据的采集、 处理、综合、运算和参数估计,并要求具有实时性,这对于常规检测和控制手段 来说是不可能做到的,必须采用在线检测技术和过程控制计算机。反过来,实施 计算机系统对发酵过程的参数估计与动态优化控制,也必须以能够描述各变量变 化速率之间关系的动力学方程(即数学模型)为基础。 发酵动力学研究的动态变量: 菌体生长比速 Xdt dX = 基质消耗比速 Xdt dS = − 产物生成比速 Xdt dP = O2 消耗比速 Xdt O2 O2 d Q = −
4.1.2 微生物反应动力学的研究特点 微生物反应动力学研究各种过程变量在活细胞作用下变化的规律,以及各种 反应条件对这些过程变量变化速度的影响。必须注意,微生物反应动力学研究的 对象既然时运动着的物质,就不能单纯地用传统的静态变量如质量、溶氧量、菌 体量等等进行描述,而必须涉及到许多动态变量,如细胞比生长率、基质比消耗 率、CO 比生成率、产物比生产率等等。这些动态变量一般不能直接测量,只能 根据动力学方程式间接估计。 发酵过程的传统控制方法,是凭经验对一些静态变量如 pH、溶氧、残余基 质浓度等按设定点进行孤立控制,它没有系统考虑各变量之间的内在联系,也未 能反映发酵过程的动态特性,因而带有很大的局限性和盲目性。例如,pH 的控 制可用加入酸、碱或者增加培养基中的缓冲成分,或者调节各种基质的补加率来 维持生理酸、碱性物质的代谢平衡的方法在同一水平上实施,但可能出现截然不 同的结果。又如,为了维持某一水平的基质浓度,采用高水平的碳、氮平衡补料 或低水平的碳、氮平衡补料,必然产生大相径庭的结果。还有,以高菌体浓度、 低生长率或低菌体浓度、高生长率达到同一溶氧水平,结果也大不相同。 要对发酵过程进行优化控制,必须了解达到高产所必须具备的生产菌株生长 状态(生长速率、形态、浓度等),相应的基质和氧的需要率,以及各种发酵条 件对这种生长状态和需要量的影响。由于发酵动力学是关于微生物生长率、基质 和氧消耗率、产物合成率等动态变量之间关系以及它们与发酵条件之间关系的学 问,因而掌握这些学问,就能更加系统(而不是孤立)、有效(而不是盲目)的 驾驭这些发酵条件和动态变量,发酵过程的控制问题也就应刃而解了。 按发酵动力学原理对发酵过程进行优化控制,涉及到许许多多数据的采集、 处理、综合、运算和参数估计,并要求具有实时性,这对于常规检测和控制手段 来说是不可能做到的,必须采用在线检测技术和过程控制计算机。反过来,实施 计算机系统对发酵过程的参数估计与动态优化控制,也必须以能够描述各变量变 化速率之间关系的动力学方程(即数学模型)为基础。 发酵动力学研究的动态变量: 菌体生长比速 Xdt dX = 基质消耗比速 Xdt dS = − 产物生成比速 Xdt dP = O2 消耗比速 Xdt O2 O2 d Q = −

CO2 生成比速 Xdt CO2 CO2 d Q = 式中 X 为菌体浓度(菌体量通常以菌体干重表示),S 为基质浓度,P 为产 物浓度。O2 代表 O2 浓度,CO2代表 CO2浓度。 4.1.3 微生物反应的得率系数 得率系数是对碳源等物质生成菌体或其他产物的潜力进行定量评价的重要 参数。 表 4-2 微生物反应的菌体得率与产物得率 得率系数 定义式 定义式(微分形式) 菌体得率 S X YX S − / = dS dX YX S − / = 菌体得率常数 G G S X Y (− ) = G G dS dX Y (− ) = 产物得率 S P YP S − / = dS dP YP S − / = 产物得率常数 P P S P Y (− ) = P P dS dP Y (− ) = 相对氧的菌体得率 2 / O X YX O − = 2 / dO dX YX O = 相对氧的菌体得率常数 G GO O X Y ( ) − 2 = G GO dO dX Y ( ) − 2 = 相对氧的产物得率 2 / O P YP O − = 2 / dO dP YP O − = 相对氧的产物得率常数 G PO O P Y ( ) − 2 = G PO dO dP Y ( ) − 2 = 相对自由能的菌体得率 E X YkJ = 例 3 求例 2 中酵母细胞培养的 YX / S 和 YX /O 。 解:由例 2 中系数计算结果可确定微生物反应式为 C2H5OH + 2.394O2 + 0.085NH3 → 0.564CH1.7 5N0.1 5O0.5 +1.436CO2 + 2.634H2O 0.292 12 2 6 16 0.564 (12 1.75 14 0.15 16 0.5) / = + + + + + YX S = 0.176 2.394 32 0.564 (12 1.75 14 0.15 16 0.5) / = + + + YX O =
CO2 生成比速 Xdt CO2 CO2 d Q = 式中 X 为菌体浓度(菌体量通常以菌体干重表示),S 为基质浓度,P 为产 物浓度。O2 代表 O2 浓度,CO2代表 CO2浓度。 4.1.3 微生物反应的得率系数 得率系数是对碳源等物质生成菌体或其他产物的潜力进行定量评价的重要 参数。 表 4-2 微生物反应的菌体得率与产物得率 得率系数 定义式 定义式(微分形式) 菌体得率 S X YX S − / = dS dX YX S − / = 菌体得率常数 G G S X Y (− ) = G G dS dX Y (− ) = 产物得率 S P YP S − / = dS dP YP S − / = 产物得率常数 P P S P Y (− ) = P P dS dP Y (− ) = 相对氧的菌体得率 2 / O X YX O − = 2 / dO dX YX O = 相对氧的菌体得率常数 G GO O X Y ( ) − 2 = G GO dO dX Y ( ) − 2 = 相对氧的产物得率 2 / O P YP O − = 2 / dO dP YP O − = 相对氧的产物得率常数 G PO O P Y ( ) − 2 = G PO dO dP Y ( ) − 2 = 相对自由能的菌体得率 E X YkJ = 例 3 求例 2 中酵母细胞培养的 YX / S 和 YX /O 。 解:由例 2 中系数计算结果可确定微生物反应式为 C2H5OH + 2.394O2 + 0.085NH3 → 0.564CH1.7 5N0.1 5O0.5 +1.436CO2 + 2.634H2O 0.292 12 2 6 16 0.564 (12 1.75 14 0.15 16 0.5) / = + + + + + YX S = 0.176 2.394 32 0.564 (12 1.75 14 0.15 16 0.5) / = + + + YX O =

4.1.4 微生物反应的维持常数 碳源维持常数 m:单位质量的菌体单位时间内维持生存所需的碳源。 氧维持常数 mo:单位质量的菌体单位时间内维持生存所需氧气。 ATP 维持常数 mATP:单位质量的菌体单位时间内维持生存所需 ATP。 4.1.5 微生物反应过程的质量衡算 4.1.5.1 碳素平衡 3 4 2 1 2 dt dP dt dCO dt dX dt dS = + + − (4-1) 或: 1 2 2 3 4 = + QCO + (4-2) 式中: α1 — 每摩尔基质中碳的含量(g/mol),如葡萄糖 α1= 72 α2 — 每克(干)菌体内碳的含量(g/g),一般 α2 = 0.5 α3 — 每摩尔二氧化碳中碳的含量(g/mol),α3 = 12 α4 — 每摩尔产物中碳的含量(g/mol),对乙醇 α4 =24,对醋酸 α4=24,对乳 酸 α4=36。 4.1.5.2. 碳源恒算 在微生物反应过程中碳源主要消耗于: (1) 满足于微生物菌体生长的需要,可用(∆S)G 表示。 (2) 维持微生物生存的消耗,可用(∆S)m 表示。 (3) 生成代谢产物的消耗,可用(∆S)P 表示。 则有: −∆S = (−∆S)G + (−∆S)m + (−∆S)P (4-3) 表示为微分形式,方程两侧同除 dt,得 G m dt P dS dt dS dt dS dt dS + − + − − = − (4-4) 根据得率常数的定义,(4-4)式可变形为 + + − = dt dP Y m X dt dX dt Y dS G P 1 1 (4-5) 两侧同除 X,得 G YP m Y 1 1 = + + (4-6) 在以培养微生物细胞为目的的微生物反应过程中,代谢产物的积累可以忽略
4.1.4 微生物反应的维持常数 碳源维持常数 m:单位质量的菌体单位时间内维持生存所需的碳源。 氧维持常数 mo:单位质量的菌体单位时间内维持生存所需氧气。 ATP 维持常数 mATP:单位质量的菌体单位时间内维持生存所需 ATP。 4.1.5 微生物反应过程的质量衡算 4.1.5.1 碳素平衡 3 4 2 1 2 dt dP dt dCO dt dX dt dS = + + − (4-1) 或: 1 2 2 3 4 = + QCO + (4-2) 式中: α1 — 每摩尔基质中碳的含量(g/mol),如葡萄糖 α1= 72 α2 — 每克(干)菌体内碳的含量(g/g),一般 α2 = 0.5 α3 — 每摩尔二氧化碳中碳的含量(g/mol),α3 = 12 α4 — 每摩尔产物中碳的含量(g/mol),对乙醇 α4 =24,对醋酸 α4=24,对乳 酸 α4=36。 4.1.5.2. 碳源恒算 在微生物反应过程中碳源主要消耗于: (1) 满足于微生物菌体生长的需要,可用(∆S)G 表示。 (2) 维持微生物生存的消耗,可用(∆S)m 表示。 (3) 生成代谢产物的消耗,可用(∆S)P 表示。 则有: −∆S = (−∆S)G + (−∆S)m + (−∆S)P (4-3) 表示为微分形式,方程两侧同除 dt,得 G m dt P dS dt dS dt dS dt dS + − + − − = − (4-4) 根据得率常数的定义,(4-4)式可变形为 + + − = dt dP Y m X dt dX dt Y dS G P 1 1 (4-5) 两侧同除 X,得 G YP m Y 1 1 = + + (4-6) 在以培养微生物细胞为目的的微生物反应过程中,代谢产物的积累可以忽略

不计的情况下,(4-6)式可以简化为: m YG = + 1 (4-7) 因此采用直线作图法可测定参数 YG 和 m。 4.1.5.3 氧衡算 微生物反应过程中的耗氧量由三部分组成,一部分用于微生物维持生命活动 的耗氧,一部分为生长菌体的耗氧,另一部分为产物耗氧。即: ∆O2 = (∆O2)m + (∆O2)G +(∆O2)P (4-8) 表示为微分形式,两侧同除 dt, G m P dt dO dt dO dt dO dt dO + − + − − = − 2 2 2 2 (4-9) 根据氧得率常数的定义,(4-9)式可变形为 dt dP Y m X dt dX dt Y dO PO o GO 2 1 1 − = + + (4-10) 两侧同除 X,得 GO o GO O Y m Y Q 1 1 2 = + + (4-11) 例 4:乙醇为碳源,进行酵母好氧培养,结果如下: (h-1 ) 0.020 0.055 0.095 0.115 0.119 O2 Q [g/(gh)] 0.0278 0.0589 0.0909 0.111 0.115 解:根据氧衡算, GO o GO O Y m Y Q 1 1 2 = + + ,因产物可忽略不计,所以, o GO O m Y Q = + 1 2 ,以 QO2~μ绘图,为一直线,直线的截距为 m0,斜率为 YGO 1 。 根据实验数据绘制实验曲线。 由图中可知:m0 =0.01[g/(gh)], YGO 1 =0.8717, 解得:m0 =0.01[g/(gh)],YGO=1.15(g/g)
不计的情况下,(4-6)式可以简化为: m YG = + 1 (4-7) 因此采用直线作图法可测定参数 YG 和 m。 4.1.5.3 氧衡算 微生物反应过程中的耗氧量由三部分组成,一部分用于微生物维持生命活动 的耗氧,一部分为生长菌体的耗氧,另一部分为产物耗氧。即: ∆O2 = (∆O2)m + (∆O2)G +(∆O2)P (4-8) 表示为微分形式,两侧同除 dt, G m P dt dO dt dO dt dO dt dO + − + − − = − 2 2 2 2 (4-9) 根据氧得率常数的定义,(4-9)式可变形为 dt dP Y m X dt dX dt Y dO PO o GO 2 1 1 − = + + (4-10) 两侧同除 X,得 GO o GO O Y m Y Q 1 1 2 = + + (4-11) 例 4:乙醇为碳源,进行酵母好氧培养,结果如下: (h-1 ) 0.020 0.055 0.095 0.115 0.119 O2 Q [g/(gh)] 0.0278 0.0589 0.0909 0.111 0.115 解:根据氧衡算, GO o GO O Y m Y Q 1 1 2 = + + ,因产物可忽略不计,所以, o GO O m Y Q = + 1 2 ,以 QO2~μ绘图,为一直线,直线的截距为 m0,斜率为 YGO 1 。 根据实验数据绘制实验曲线。 由图中可知:m0 =0.01[g/(gh)], YGO 1 =0.8717, 解得:m0 =0.01[g/(gh)],YGO=1.15(g/g)

4.1.6 微生物反应的能量衡算 4.1.6.1 有效电子转移和有机物氧化焓变 物质的氧化总伴随着电子的转移。在氧化过程中,每分子氧可以接受 4 个电 子。我们把物质在氧化过程中伴随着能量释放所进行的电子转移称为“有效电 子转移”。例如:0.5mol 氧气与 1mol 氢气化合形成 1mol 水蒸汽,同时放出 241.4KJ 热量,过程中有效电子转移数为 2,记作 2(av,e- )。当 1mol 葡萄糖完全氧化时, 需要消耗 6mol 的氧,相应的有效电子转移数为:64=24(av,e- /mol)。从大量实验 得到,有机化合物氧化时每转移一个有效电子,平均释放出 111KJ 的热量,记作: ∆Hav,e- = -111KJ/ av,e- 因此,葡萄糖完全氧化释放的能量应为: ∆Hs* =(-111)24 = -2664KJ/mol 但是,当我们用量热器测定葡萄糖燃烧过程得到的是:∆Hs= - 2816kJ/mol, 两者相差在 5%左右,这样的误差在工程上是允许的。因此可以用有效电子转移 数来计算有机物氧化所释放的能量,这在工程上是十分方便的。任何有机物只要 写出其氧化的反应方程式,根据反应式中所消耗氧的摩尔数,就可以计算出反应 所释放的能量。为了区别有机物氧化实际焓变和通过有效电子转移的计算值,分 别用∆H 和∆H*表示,后者称为有机物氧化以有效电子转移为基准的“焓变”。 由于微生物反应过程一般是在 25~37℃温度范围内进行的,以葡萄糖作碳源 为例,在发酵过程中,碳源完全氧化相应的标准自由能变化的计算如下: C6H12O6 + 6O2 6CO2 + 6H2O 过程熵变为: ∆S 0 = − 0 0 S产物 S反应物 = ( 0 0 2 2 6SCO + 6S H O )-( 0 0 6 12 6 2 6SC H O + 6SO ) y = 0.8717x + 0.0103 R 2 = 0.9988 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0 0.05 0.1 0.15 μ(1/h) QO2 [g/(gh)]
4.1.6 微生物反应的能量衡算 4.1.6.1 有效电子转移和有机物氧化焓变 物质的氧化总伴随着电子的转移。在氧化过程中,每分子氧可以接受 4 个电 子。我们把物质在氧化过程中伴随着能量释放所进行的电子转移称为“有效电 子转移”。例如:0.5mol 氧气与 1mol 氢气化合形成 1mol 水蒸汽,同时放出 241.4KJ 热量,过程中有效电子转移数为 2,记作 2(av,e- )。当 1mol 葡萄糖完全氧化时, 需要消耗 6mol 的氧,相应的有效电子转移数为:64=24(av,e- /mol)。从大量实验 得到,有机化合物氧化时每转移一个有效电子,平均释放出 111KJ 的热量,记作: ∆Hav,e- = -111KJ/ av,e- 因此,葡萄糖完全氧化释放的能量应为: ∆Hs* =(-111)24 = -2664KJ/mol 但是,当我们用量热器测定葡萄糖燃烧过程得到的是:∆Hs= - 2816kJ/mol, 两者相差在 5%左右,这样的误差在工程上是允许的。因此可以用有效电子转移 数来计算有机物氧化所释放的能量,这在工程上是十分方便的。任何有机物只要 写出其氧化的反应方程式,根据反应式中所消耗氧的摩尔数,就可以计算出反应 所释放的能量。为了区别有机物氧化实际焓变和通过有效电子转移的计算值,分 别用∆H 和∆H*表示,后者称为有机物氧化以有效电子转移为基准的“焓变”。 由于微生物反应过程一般是在 25~37℃温度范围内进行的,以葡萄糖作碳源 为例,在发酵过程中,碳源完全氧化相应的标准自由能变化的计算如下: C6H12O6 + 6O2 6CO2 + 6H2O 过程熵变为: ∆S 0 = − 0 0 S产物 S反应物 = ( 0 0 2 2 6SCO + 6S H O )-( 0 0 6 12 6 2 6SC H O + 6SO ) y = 0.8717x + 0.0103 R 2 = 0.9988 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0 0.05 0.1 0.15 μ(1/h) QO2 [g/(gh)]

=(6×0.213+6×0.0698)-(0.212+6×0.205) = 0.255kJ/kmol 标准自由能变化由于: T∆S 0=(298~310) ×0.255=76~79kJ/mol<<-∆Hs*=2664kJ/mol 则有:∆ 6 0 GC6H12O = ∆Hs ∆Hs* = -2664kJ/mol 因此,微生物反应过程基质和产物的标准自由能变化可近似等于其焓变。 4.1.6.2 自由能消耗对菌体得率 YKJ 菌体所保持的自由能 微生物反应过程的自由能变化 菌体增长量 + YKJ = = 增长菌体的氧化焓变 微生物反应过程的氧化焓变 菌体增长量 + 即 ( )( ) ( ) a C KJ H X H X Y − + − = (4-12) 讨论: 1) 最低培养基中进行通风培养 由于培养基内葡萄糖是唯一碳源,它既作为能源,又作为构成细胞的材料。 ( )( ) ( )( ) 2 * H X H0 O X Y a KJ − + − = = Ha H YX / O * 0 ( ) / 1 − − (4-13) 式中:−∆H0 *:微生物呼吸(耗氧)反应的焓变 − ∆Ha:以菌体燃烧热为基准的焓变。取- ∆Ha= -22.15kJ/g 2)最低培养基中进行厌氧培养 葡萄糖既作为能源,又作为构成细胞的材料。构成菌体以外的碳源消耗为 X 1 2 ,构成菌体以外的碳源消耗为∆S− X 1 2 ,所以 − + − − − − − = ( )( ) ( )( ) ( )( ) 1 2 H X H S X H P X Y a S P KJ = − a X S − S − X S + P P S X S H Y H Y H Y Y / / 1 2 / / ( ) (1 ) ( ) (4-14)
=(6×0.213+6×0.0698)-(0.212+6×0.205) = 0.255kJ/kmol 标准自由能变化由于: T∆S 0=(298~310) ×0.255=76~79kJ/mol<<-∆Hs*=2664kJ/mol 则有:∆ 6 0 GC6H12O = ∆Hs ∆Hs* = -2664kJ/mol 因此,微生物反应过程基质和产物的标准自由能变化可近似等于其焓变。 4.1.6.2 自由能消耗对菌体得率 YKJ 菌体所保持的自由能 微生物反应过程的自由能变化 菌体增长量 + YKJ = = 增长菌体的氧化焓变 微生物反应过程的氧化焓变 菌体增长量 + 即 ( )( ) ( ) a C KJ H X H X Y − + − = (4-12) 讨论: 1) 最低培养基中进行通风培养 由于培养基内葡萄糖是唯一碳源,它既作为能源,又作为构成细胞的材料。 ( )( ) ( )( ) 2 * H X H0 O X Y a KJ − + − = = Ha H YX / O * 0 ( ) / 1 − − (4-13) 式中:−∆H0 *:微生物呼吸(耗氧)反应的焓变 − ∆Ha:以菌体燃烧热为基准的焓变。取- ∆Ha= -22.15kJ/g 2)最低培养基中进行厌氧培养 葡萄糖既作为能源,又作为构成细胞的材料。构成菌体以外的碳源消耗为 X 1 2 ,构成菌体以外的碳源消耗为∆S− X 1 2 ,所以 − + − − − − − = ( )( ) ( )( ) ( )( ) 1 2 H X H S X H P X Y a S P KJ = − a X S − S − X S + P P S X S H Y H Y H Y Y / / 1 2 / / ( ) (1 ) ( ) (4-14)