
2 酶促反应动力学 教学基本内容: 酶促反应的特点;单底物酶促反应动力学方程(米氏方程)的推导;抑制剂 对酶促反应的影响,竞争性抑制和非竞争性抑制酶促反应动力学方程的推导;产 物抑制、底物抑制的概念,产物抑制和底物抑制酶促反应动力学方程的推导;多 底物酶促反应的机制,双底物酶促反应动力学的推导;固定化酶的概念,常见的 酶的固定化方法,固定化对酶性质的影响及固定化对酶促反应的影响,外扩散过 程和内扩散过程分析;酶的失活动力学。 2.1 酶促反应动力学的特点 2.2 均相酶促反应动力学 2.2.1 酶促反应动力学基础 2.2.2 单底物酶促反应动力学 2.2.3 抑制剂对酶促反应速率的影响 2.2.4 多底物酶促反应动力学 2.3 固定化酶促反应动力学 2.4 酶的失活动力学 授课重点: 1. 酶的应用研究与经典酶学研究的联系与区别 2. 米氏方程。 3 竞争性抑制酶促反应动力学方程。 4. 非竞争性抑制酶促反应动力学方程。 5. 产物抑制酶促反应动力学方程。 6. 底物抑制酶促反应动力学方程。 7. 双底物酶促反应动力学方程。 8. 外扩散对固定化酶促反应动力学的影响,Da 准数的概念。 9. 内扩散对固定化酶促反应动力学的影响,φ 准数的概念。 10. 酶的失活动力学。 难点: 1. 采用稳态法和快速平衡法建立酶促反应动力学方程。 2. 固定化对酶促反应的影响,五大效应(分子构象的改变、位阻效应、微扰 效应、分配效应及扩散效应)的区分。 3. 内扩散过程分析,涉及到对微元单位进行物料衡算和二阶微分方程的求
2 酶促反应动力学 教学基本内容: 酶促反应的特点;单底物酶促反应动力学方程(米氏方程)的推导;抑制剂 对酶促反应的影响,竞争性抑制和非竞争性抑制酶促反应动力学方程的推导;产 物抑制、底物抑制的概念,产物抑制和底物抑制酶促反应动力学方程的推导;多 底物酶促反应的机制,双底物酶促反应动力学的推导;固定化酶的概念,常见的 酶的固定化方法,固定化对酶性质的影响及固定化对酶促反应的影响,外扩散过 程和内扩散过程分析;酶的失活动力学。 2.1 酶促反应动力学的特点 2.2 均相酶促反应动力学 2.2.1 酶促反应动力学基础 2.2.2 单底物酶促反应动力学 2.2.3 抑制剂对酶促反应速率的影响 2.2.4 多底物酶促反应动力学 2.3 固定化酶促反应动力学 2.4 酶的失活动力学 授课重点: 1. 酶的应用研究与经典酶学研究的联系与区别 2. 米氏方程。 3 竞争性抑制酶促反应动力学方程。 4. 非竞争性抑制酶促反应动力学方程。 5. 产物抑制酶促反应动力学方程。 6. 底物抑制酶促反应动力学方程。 7. 双底物酶促反应动力学方程。 8. 外扩散对固定化酶促反应动力学的影响,Da 准数的概念。 9. 内扩散对固定化酶促反应动力学的影响,φ 准数的概念。 10. 酶的失活动力学。 难点: 1. 采用稳态法和快速平衡法建立酶促反应动力学方程。 2. 固定化对酶促反应的影响,五大效应(分子构象的改变、位阻效应、微扰 效应、分配效应及扩散效应)的区分。 3. 内扩散过程分析,涉及到对微元单位进行物料衡算和二阶微分方程的求

解、无因次变换、解析解与数值解等问题。 4.温度对酶促反应速率和酶的失活速率的双重影响,最适温度的概念。温度 和时间对酶失活的影响。 本章主要教学要求: 1. 掌握稳态法和快速平衡法推导酶促反应动力学方程。 2. 了解酶的固定化方法。理解固定化对酶促反应速率的影响。掌握 Da 准数 的概念及 φ 准数的概念,理解外扩散和内扩散对酶促反应速率的影响。 3. 了解酶的一步失活模型与多步失活模型,反应过程中底物对酶稳定性的 影响
解、无因次变换、解析解与数值解等问题。 4.温度对酶促反应速率和酶的失活速率的双重影响,最适温度的概念。温度 和时间对酶失活的影响。 本章主要教学要求: 1. 掌握稳态法和快速平衡法推导酶促反应动力学方程。 2. 了解酶的固定化方法。理解固定化对酶促反应速率的影响。掌握 Da 准数 的概念及 φ 准数的概念,理解外扩散和内扩散对酶促反应速率的影响。 3. 了解酶的一步失活模型与多步失活模型,反应过程中底物对酶稳定性的 影响

2 酶促反应动力学 2.1 酶促反应动力学的特点 2.1.1 酶的基本概念 2.1.2 酶的稳定性及应用特点 酶是以活力、而不是以质量购销的。 酶有不同的质量等级:工业用酶、食品用酶、医药用酶。 酶的实际应用中应注意,没有必要使用比工艺条件所需纯度更高的酶。 2.1.3 酶的应用研究与经典酶学研究的联系与区别 经典酶学研究中,酶活力的测定是在反应的初始短时间内进行的,并且酶浓 度、底物浓度较低,且为水溶液,酶学研究的目的是探讨酶促反应的机制。工业 上,为保证酶促反应高效率完成,常需要使用高浓度的酶制剂和底物,且反应要 持续较长时间,反应体系多为非均相体系,有时反应是在有机溶剂中进行。 2.2 均相酶促反应动力学 均相酶促反应动力学是以研究酶促反应机制为目的发展起来的。作为酶工程 技术人员,如果仅仅比较详细地解释了酶促反应机制和过程是不够的,还应对影 响其反应速率的因素进行定量的分析,建立可信赖的反应速率方程,并以此为基 础进行反应器的合理设计和确定反应过程的最佳条件。因此,以讨论反应机制为 目的的酶促反应动力学与为了设计与操作反应器的工业酶动力学,在研究方法上 自然不同。这与化学中的反应动力学和工业上的化学反应动力学的不同一样。 2.2.1 酶促反应动力学基础 可采用化学反应动力学方法建立酶促反应动力学方程。 对酶促反应 A B P Q k + → + ,有: A P ACB r = r = r = kC (2-1) dt dC r A A = − (2-2) dt dC r P P = (2-3) 式中, k:酶促反应速率常数; r:酶促反应速率; rA:以底物 A 的消耗速率表示的酶促反应速率; rP:以产物 P 的生成速率表示的酶促反应速率
2 酶促反应动力学 2.1 酶促反应动力学的特点 2.1.1 酶的基本概念 2.1.2 酶的稳定性及应用特点 酶是以活力、而不是以质量购销的。 酶有不同的质量等级:工业用酶、食品用酶、医药用酶。 酶的实际应用中应注意,没有必要使用比工艺条件所需纯度更高的酶。 2.1.3 酶的应用研究与经典酶学研究的联系与区别 经典酶学研究中,酶活力的测定是在反应的初始短时间内进行的,并且酶浓 度、底物浓度较低,且为水溶液,酶学研究的目的是探讨酶促反应的机制。工业 上,为保证酶促反应高效率完成,常需要使用高浓度的酶制剂和底物,且反应要 持续较长时间,反应体系多为非均相体系,有时反应是在有机溶剂中进行。 2.2 均相酶促反应动力学 均相酶促反应动力学是以研究酶促反应机制为目的发展起来的。作为酶工程 技术人员,如果仅仅比较详细地解释了酶促反应机制和过程是不够的,还应对影 响其反应速率的因素进行定量的分析,建立可信赖的反应速率方程,并以此为基 础进行反应器的合理设计和确定反应过程的最佳条件。因此,以讨论反应机制为 目的的酶促反应动力学与为了设计与操作反应器的工业酶动力学,在研究方法上 自然不同。这与化学中的反应动力学和工业上的化学反应动力学的不同一样。 2.2.1 酶促反应动力学基础 可采用化学反应动力学方法建立酶促反应动力学方程。 对酶促反应 A B P Q k + → + ,有: A P ACB r = r = r = kC (2-1) dt dC r A A = − (2-2) dt dC r P P = (2-3) 式中, k:酶促反应速率常数; r:酶促反应速率; rA:以底物 A 的消耗速率表示的酶促反应速率; rP:以产物 P 的生成速率表示的酶促反应速率

对连锁的酶促反应,如 A M P k k ⎯⎯1→ ⎯⎯2→ ,有: A A kC dt dC − = (2-4) A M M k C k C dt dC = 1 − 2 (2-5) M P k C dt dC = 2 (2-6) 2.2.2 单底物酶促反应动力学(米氏方程) 单底物不可逆酶促反应是最简单的酶促反应。水解酶、异构酶及多数裂解酶 的催化反应均属此类。 对单底物酶促反应 S → P ,根据酶-底物中间复合物假说,其反应机制可 表示为: E S ES E P k k k + → + − 1 2 1 下面我们分别采用快速平衡法和稳态法推导其动力学方程。 快速平衡法: 几点假设: (1)CS>>CE,中间复合物 ES 的形成不会降低 CS。 (2)不考虑 E + P EP 这个可逆反应。 (3) E S ES k k + − 1 1 为快速平衡, ES E P k → + 2 为整个反应的限速阶段,此 ES 分解成产物不足以破坏这个平衡。 根据以上假设,建立动力学方程: CES r k = 2 (2-7) 1 1 k k K C C C S ES E S − = = (2-8) CE0 = CE +CES (2-9) 解之,得 S S E S K C k C C r + = 2 0 (2-10) 令 max 2CE0 r = k , (2-11)
对连锁的酶促反应,如 A M P k k ⎯⎯1→ ⎯⎯2→ ,有: A A kC dt dC − = (2-4) A M M k C k C dt dC = 1 − 2 (2-5) M P k C dt dC = 2 (2-6) 2.2.2 单底物酶促反应动力学(米氏方程) 单底物不可逆酶促反应是最简单的酶促反应。水解酶、异构酶及多数裂解酶 的催化反应均属此类。 对单底物酶促反应 S → P ,根据酶-底物中间复合物假说,其反应机制可 表示为: E S ES E P k k k + → + − 1 2 1 下面我们分别采用快速平衡法和稳态法推导其动力学方程。 快速平衡法: 几点假设: (1)CS>>CE,中间复合物 ES 的形成不会降低 CS。 (2)不考虑 E + P EP 这个可逆反应。 (3) E S ES k k + − 1 1 为快速平衡, ES E P k → + 2 为整个反应的限速阶段,此 ES 分解成产物不足以破坏这个平衡。 根据以上假设,建立动力学方程: CES r k = 2 (2-7) 1 1 k k K C C C S ES E S − = = (2-8) CE0 = CE +CES (2-9) 解之,得 S S E S K C k C C r + = 2 0 (2-10) 令 max 2CE0 r = k , (2-11)
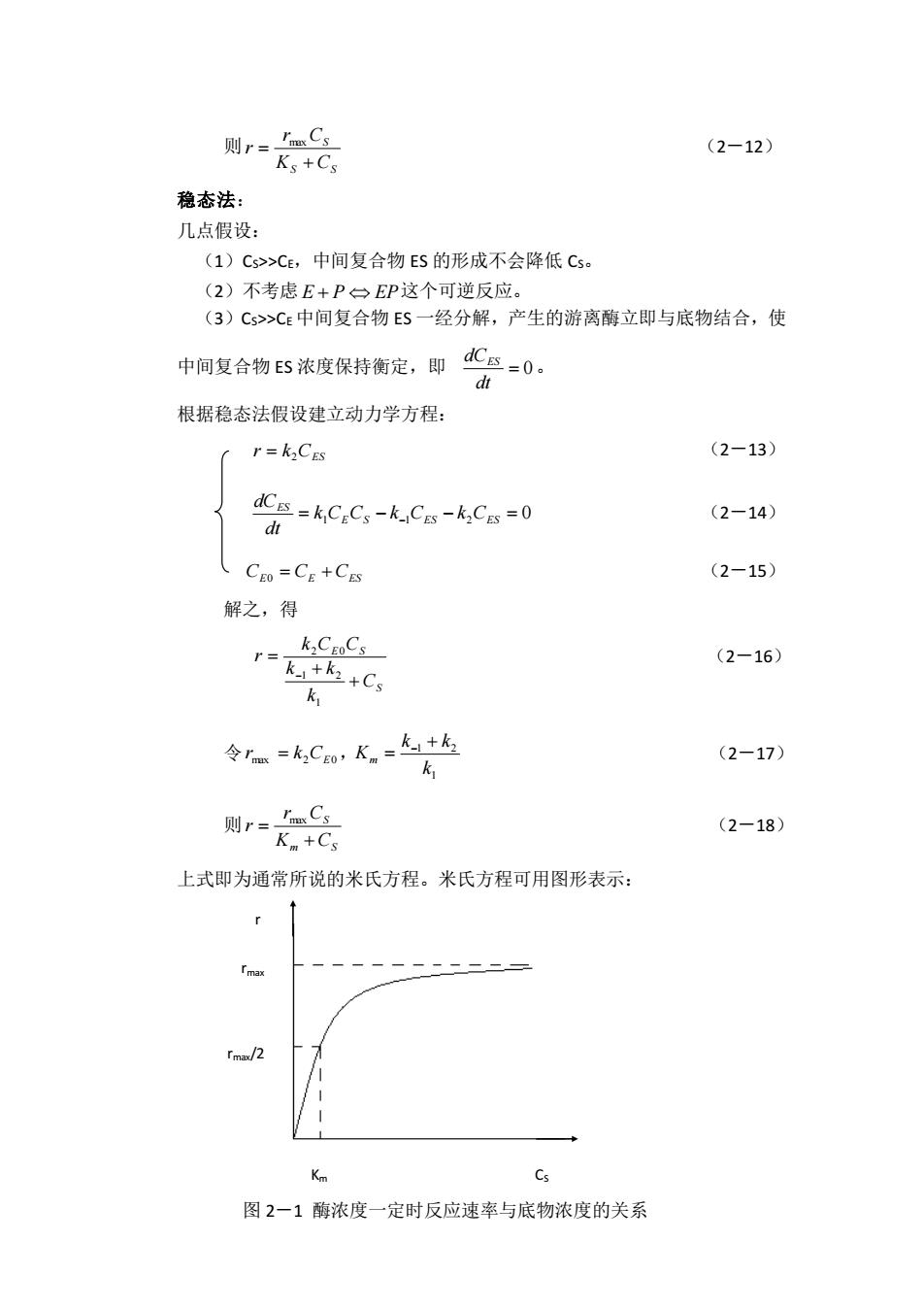
则 S S S K C r C r + = max (2-12) 稳态法: 几点假设: (1)CS>>CE,中间复合物 ES 的形成不会降低 CS。 (2)不考虑 E + P EP 这个可逆反应。 (3)CS>>CE 中间复合物 ES 一经分解,产生的游离酶立即与底物结合,使 中间复合物 ES 浓度保持衡定,即 = 0 dt dCES 。 根据稳态法假设建立动力学方程: CES r k = 2 (2-13) = 1 E S − −1 ES − 2 ES = 0 ES k C C k C k C dt dC (2-14) CE0 = CE +CES (2-15) 解之,得 S E S C k k k k C C r + + = − 1 1 2 2 0 (2-16) 令 max 2CE0 r = k , 1 1 2 k k k Km + = − (2-17) 则 m S S K C r C r + = max (2-18) 上式即为通常所说的米氏方程。米氏方程可用图形表示: r rmax rmax/2 Km CS 图 2-1 酶浓度一定时反应速率与底物浓度的关系
则 S S S K C r C r + = max (2-12) 稳态法: 几点假设: (1)CS>>CE,中间复合物 ES 的形成不会降低 CS。 (2)不考虑 E + P EP 这个可逆反应。 (3)CS>>CE 中间复合物 ES 一经分解,产生的游离酶立即与底物结合,使 中间复合物 ES 浓度保持衡定,即 = 0 dt dCES 。 根据稳态法假设建立动力学方程: CES r k = 2 (2-13) = 1 E S − −1 ES − 2 ES = 0 ES k C C k C k C dt dC (2-14) CE0 = CE +CES (2-15) 解之,得 S E S C k k k k C C r + + = − 1 1 2 2 0 (2-16) 令 max 2CE0 r = k , 1 1 2 k k k Km + = − (2-17) 则 m S S K C r C r + = max (2-18) 上式即为通常所说的米氏方程。米氏方程可用图形表示: r rmax rmax/2 Km CS 图 2-1 酶浓度一定时反应速率与底物浓度的关系

讨论: (1)当 CS>Km 时, max r = r ,属零级反应。 (3)当 CS=Km 时, 2 max r r = 。Km 在数量上等于反应速度达到最大反应速度一 半时的底物浓度。 Km 和 rmax 的测定方法 Linewear Burk 法,即双倒数法。 对米氏方程两侧取倒数,得 S m r C K r r 1 1 1 max max = + 。以 CS r 1 ~ 1 作图,得一直线, 直线斜率为 max r K m ,截距为 max 1 r 。根据直线斜率和截距可计算出 Km 和 rmax。 图 2-2 双倒数法求解 Km 和 rmax 2.2.3 温度对酶促反应速率的影响 温度对酶促反应速率的影响,是通过影响 k2 和 KS( Km )实现的。 exp( ) 2 RT Ea k = A − Arrhenius 方程 (2-34) exp( ) RT H KS − Van’t-Hoff 方程 (2-35) 值得注意的是 Arrhenius 方程仅在较低温度下适用于酶促反应。过高的温度 将导致酶的失活(见教材 P23 图 2-4)。(2-35)式中 H 为反应热。 -1/Km 1/rmax 1/r 斜率-Km/rmax 1/CS
讨论: (1)当 CS>Km 时, max r = r ,属零级反应。 (3)当 CS=Km 时, 2 max r r = 。Km 在数量上等于反应速度达到最大反应速度一 半时的底物浓度。 Km 和 rmax 的测定方法 Linewear Burk 法,即双倒数法。 对米氏方程两侧取倒数,得 S m r C K r r 1 1 1 max max = + 。以 CS r 1 ~ 1 作图,得一直线, 直线斜率为 max r K m ,截距为 max 1 r 。根据直线斜率和截距可计算出 Km 和 rmax。 图 2-2 双倒数法求解 Km 和 rmax 2.2.3 温度对酶促反应速率的影响 温度对酶促反应速率的影响,是通过影响 k2 和 KS( Km )实现的。 exp( ) 2 RT Ea k = A − Arrhenius 方程 (2-34) exp( ) RT H KS − Van’t-Hoff 方程 (2-35) 值得注意的是 Arrhenius 方程仅在较低温度下适用于酶促反应。过高的温度 将导致酶的失活(见教材 P23 图 2-4)。(2-35)式中 H 为反应热。 -1/Km 1/rmax 1/r 斜率-Km/rmax 1/CS

2.2.4 抑制剂对酶促反应速率的影响 首先应搞清失活作用与抑制作用的异同。 失活作用:指物理或化学因素部分或全部破坏了酶的三维结构,引起酶的 变性,导致酶部分或全部丧失活性。 抑制作用:指酶在不变性条件下,由于活性中心化学性质的改变而引起酶 活性的降低或丧失。 凡能使酶的活性下降而不引起酶蛋白变性的物质称做酶的抑制剂(inhibitor)。 使酶变性失活(称为酶的钝化)的因素如强酸、强碱等,不属于抑制剂。通常抑制 作用分为可逆性抑制和不可逆性抑制两类。 2.2.4.1 竞争性抑制 图 2-3 竞争性抑制作用示意图 反应机理: E S ES E P k k k + → + − 1 2 1 (2-36) E I EI KI + (2-37) 采用快速平衡法推导动力学方程: CES r k = 2 (2-38) S ES E S K k k C C C = = − 1 1 (2-39) I EI E I K C C C = (2-40) CE0 = CE +CES +CEI (2-41) 解之,得 S I I S S K C K C r C r + + = (1 / ) max (2-42) E S I
2.2.4 抑制剂对酶促反应速率的影响 首先应搞清失活作用与抑制作用的异同。 失活作用:指物理或化学因素部分或全部破坏了酶的三维结构,引起酶的 变性,导致酶部分或全部丧失活性。 抑制作用:指酶在不变性条件下,由于活性中心化学性质的改变而引起酶 活性的降低或丧失。 凡能使酶的活性下降而不引起酶蛋白变性的物质称做酶的抑制剂(inhibitor)。 使酶变性失活(称为酶的钝化)的因素如强酸、强碱等,不属于抑制剂。通常抑制 作用分为可逆性抑制和不可逆性抑制两类。 2.2.4.1 竞争性抑制 图 2-3 竞争性抑制作用示意图 反应机理: E S ES E P k k k + → + − 1 2 1 (2-36) E I EI KI + (2-37) 采用快速平衡法推导动力学方程: CES r k = 2 (2-38) S ES E S K k k C C C = = − 1 1 (2-39) I EI E I K C C C = (2-40) CE0 = CE +CES +CEI (2-41) 解之,得 S I I S S K C K C r C r + + = (1 / ) max (2-42) E S I

式中, max 2CE0 r = k , 1 1 k k KS − = 采用稳态法推导动力学方程: CES r k = 2 (2- 43) = 1 E S − −1 ES − 2 ES = 0 ES k C C k C k C dt dC (2- 44) = i E I − −i EI = 0 EI k C C k C dt dC (2- 45) CE0 = CE +CES +CEI (2- 46) 解之,得 m I I S S K C K C r C r + + = (1 / ) max (2- 47) 式中: max 2CE0 r = k , 1 1 2 k k k Km + = − 令 (1 / ) Km = Km +CI KI ,(2-47)式可变形为 m S S K C r C r + = max (2- 48) 式中 Km Km 将(2-48)式与米氏方程比较,可知最大反应速率测有变化,而 Km 增大。 以 CS r 1 ~ 1 作图,得一直线,直线斜率为 max r K m ,截距为 max 1 r ,如图 2-3 所示。 1/r 1/CS 1/rmax -1/Km -1/Km’ CI = 0 CI
式中, max 2CE0 r = k , 1 1 k k KS − = 采用稳态法推导动力学方程: CES r k = 2 (2- 43) = 1 E S − −1 ES − 2 ES = 0 ES k C C k C k C dt dC (2- 44) = i E I − −i EI = 0 EI k C C k C dt dC (2- 45) CE0 = CE +CES +CEI (2- 46) 解之,得 m I I S S K C K C r C r + + = (1 / ) max (2- 47) 式中: max 2CE0 r = k , 1 1 2 k k k Km + = − 令 (1 / ) Km = Km +CI KI ,(2-47)式可变形为 m S S K C r C r + = max (2- 48) 式中 Km Km 将(2-48)式与米氏方程比较,可知最大反应速率测有变化,而 Km 增大。 以 CS r 1 ~ 1 作图,得一直线,直线斜率为 max r K m ,截距为 max 1 r ,如图 2-3 所示。 1/r 1/CS 1/rmax -1/Km -1/Km’ CI = 0 CI

图 2-4 竞争性抑制作用下 CS r 1 ~ 1 曲线 2.2.4.2 非竞争性抑制 图 2-5 非竞争性抑制作用示意图 反应机理: E S ES E P k k k + → + − 1 2 1 (2 -49) E I EI KI + (2 -50) ES I ESI KI + (2 -51) 采用快速平衡法推导动力学方程: CES r k = 2 (2 -52) S ES E S K k k C C C = = − 1 1 (2 -53) I EI E I K C C C = (2 -54) I ESI ES I K C C C = (2 E S I
图 2-4 竞争性抑制作用下 CS r 1 ~ 1 曲线 2.2.4.2 非竞争性抑制 图 2-5 非竞争性抑制作用示意图 反应机理: E S ES E P k k k + → + − 1 2 1 (2 -49) E I EI KI + (2 -50) ES I ESI KI + (2 -51) 采用快速平衡法推导动力学方程: CES r k = 2 (2 -52) S ES E S K k k C C C = = − 1 1 (2 -53) I EI E I K C C C = (2 -54) I ESI ES I K C C C = (2 E S I

-55) CE0 = CE +CES +CEI (2 -56) 解之,得 (1 / )( ) max I I S S S C K K C r C r + + = (2 -57) 式中, max 2CE0 r = k , 1 1 k k KS − = 采用稳态法推导动力学方程: CES r k = 2 (2 -58) = 1 E S − −1 ES − 2 ES + −i ESI − i ES I = 0 ES k C C k C k C k C k C C dt dC (2 -59) = i E I − −i EI = 0 EI k C C k C dt dC (2 -60) = i ES I − −i ESI = 0 ESI k C C k C dt dC (2 -61) CE0 = CE +CES +CEI +CESI (2 -62) 解之,得 (1 / )( ) max I I m S S C K K C r C r + + = (2 -63) 式中, max 2CE0 r = k , 1 1 2 k k k Km + = − 令 CI KI r r 1 / ' max max + = ,(2-63)式可变形为
-55) CE0 = CE +CES +CEI (2 -56) 解之,得 (1 / )( ) max I I S S S C K K C r C r + + = (2 -57) 式中, max 2CE0 r = k , 1 1 k k KS − = 采用稳态法推导动力学方程: CES r k = 2 (2 -58) = 1 E S − −1 ES − 2 ES + −i ESI − i ES I = 0 ES k C C k C k C k C k C C dt dC (2 -59) = i E I − −i EI = 0 EI k C C k C dt dC (2 -60) = i ES I − −i ESI = 0 ESI k C C k C dt dC (2 -61) CE0 = CE +CES +CEI +CESI (2 -62) 解之,得 (1 / )( ) max I I m S S C K K C r C r + + = (2 -63) 式中, max 2CE0 r = k , 1 1 2 k k k Km + = − 令 CI KI r r 1 / ' max max + = ,(2-63)式可变形为