
第9卷第4期 智能系统学报 Vol.9 No.4 2014年8月 CAAI Transactions on Intelligent Systems Agu.2014 D0I:10.3969/j.issn.1673-4785.201308013 网络出版t地址:http://www.cnki.net/kcms/doi/10.3969/j.issn.1673-4785.201308013.html 带有高斯扰动的混沌神经网络及应用 许楠,刘桂阳,徐耀群 (1.黑龙江八一农垦大学信息技术学院,黑龙江大庆163319:2.哈尔滨商业大学系统工程研究所,黑龙江哈尔滨150028) 摘要:为考查新型混沌神经网络的抗干扰能力,在Chn's混沌神经网络模型的内部状态中加入高斯函数扰动项。 通过分析该网络神经元的混沌特性,说明了模拟退火参数及高斯函数的宽度参数对混沌行为的影响:分析了不同宽 度值时的高斯曲线以及内部状态随迭代次数的变化情况,说明了扰动强弱敏感依赖于该参数的取值。将带有高斯 扰动的混沌神经网络模型应用于解决旅行商最短路径问题(TS),通过仿真实验,说明若合理调整网络参数以及径 向基宽度参数,则该新型网络可以具有较高的抗扰动能力,从而使得网络能够避免陷入局部极小点,并以较快速度 求得全局最优解。 关键词:高斯函数;扰动:混沌神经网络:内部状态 中图分类号:TP18文献标志码:A文章编号:1673-4785(2014)04-444-05 中文引用格式:许楠,刘桂阳,徐耀群.带有高斯扰动的混沌神经网络及应用[J].智能系统学报,2014,9(4):444-448. 英文引用格式:XU Nan,LIU Guiyang,XU Yaoqun.A novel chaotic neural network with Gaussian disturbance and its application J].CAAI Transactions on Intelligent Systems,2014,9(4):444-448. A novel chaotic neural network with Gaussian disturbance and its application XU Nan',LIU Guiyang',XU Yaoqun2 (1.College of Information Technology,Heilongjiang Bayi Agricultural University,Daging 163319,China;2.Institute of System Engi- neering,Harbin University of Commerce,Harbin 150028,China) Abstract:A Gaussian function disturbance item is added into the internal state of Chen's chaotic neural network for examining the anti-disturbance ability of the new chaotic neural network.The chaotic dynamics behavior of the sin- gle chaotic neuron is analyzed.The chaotic behavior is affected by the parameter of the simulated annealing and the width of the Gaussian function.The Gaussian curve and the change of the inside state are analyzed in different widths.The amount of disturbance depends on the width.This chaotic neural network with Gaussian disturbance is used to solve traveling salesman problem.The simulation results indicate that this network can avoid the limits of being trapped into the local minima and its capability of resisting the disturbance is perfect. Keywords:Gaussian function:Gaussian disturbance:chaotic neural network:inside state 制造混沌神经计算机一直是人们追求的目标,同时对网络的应用产生一定影响,影响严重时会导 然而由于元器件的不稳定性,在一定情况下势必会 致网络失稳,因此研究神经网络的抗扰动能力是有 出现微小扰动从而对网络模型产生影响,扰动的引 必要的。高斯函数是径向基函数山的一种,同其他 入使得混沌神经网络具有更加复杂的动力学特性, 径向基函数一样存在宽度参数,本文在Chen's混沌 神经网络基础上引入高斯函数扰动,对网络内部状 收稿日期:2013-08-08.网络出版日期:2014-06-21. 态进行改进,分析了混沌神经元模型的动力学特性, 基金项目:黑龙江省教育厅科学技术研究资助项目(面上)(12531456). 通信作者:许楠.E-mail:xuaoe80@126.com. 以及宽度参数对扰动强弱的影响,在此基础上研究
第 怨 卷第 源 期摇摇摇摇摇 摇摇摇 摇摇摇 摇摇摇 智 能 系 统 学 报摇摇摇摇摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 灾燥造援怨 翼援源 圆园员源 年 愿 月摇摇摇摇摇摇摇摇摇摇摇摇 悦粤粤陨 栽则葬灶泽葬糟贼蚤燥灶泽 燥灶 陨灶贼藻造造蚤早藻灶贼 杂赠泽贼藻皂泽 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 粤早怎援 圆园员源 阅韵陨院员园援猿怨远怨 辕 躁援蚤泽泽灶援员远苑猿鄄源苑愿缘援圆园员猿园愿园员猿 网络出版地址院澡贼贼责院 辕 辕 憎憎憎援糟灶噪蚤援灶藻贼 辕 噪糟皂泽 辕 凿燥蚤 辕 员园援猿怨远怨 辕 躁援蚤泽泽灶援员远苑猿鄄源苑愿缘援圆园员猿园愿园员猿援澡贼皂造 带有高斯扰动的混沌神经网络及应用 许楠员 袁 刘桂阳员 袁徐耀群圆 渊员援黑龙江八一农垦大学 信息技术学院袁黑龙江 大庆 员远猿猿员怨曰 圆援哈尔滨商业大学 系统工程研究所袁黑龙江 哈尔滨 员缘园园圆愿冤 摘 要院为考查新型混沌神经网络的抗干扰能力袁在 悦澡藻灶爷 泽 混沌神经网络模型的内部状态中加入高斯函数扰动项遥 通过分析该网络神经元的混沌特性袁说明了模拟退火参数及高斯函数的宽度参数对混沌行为的影响曰分析了不同宽 度值时的高斯曲线以及内部状态随迭代次数的变化情况袁说明了扰动强弱敏感依赖于该参数的取值遥 将带有高斯 扰动的混沌神经网络模型应用于解决旅行商最短路径问题渊 栽杂孕冤 袁通过仿真实验袁说明若合理调整网络参数以及径 向基宽度参数袁则该新型网络可以具有较高的抗扰动能力袁从而使得网络能够避免陷入局部极小点袁并以较快速度 求得全局最优解遥 关键词院高斯函数曰扰动曰混沌神经网络曰内部状态 中图分类号院 栽孕员愿 摇 文献标志码院粤摇 文章编号院员远苑猿鄄源苑愿缘渊圆园员源冤园源鄄源源源鄄园缘 中文引用格式院许楠袁 刘桂阳 袁徐耀群援 带有高斯扰动的混沌神经网络及应用咱允暂援 智能系统学报袁 圆园员源袁 怨渊源冤 院 源源源鄄源源愿援 英文引用格式院载哉 晕葬灶袁 蕴陨哉 郧怎蚤赠葬灶早袁 载哉 再葬燥择怎灶援 粤 灶燥增藻造 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪 憎蚤贼澡 郧葬怎泽泽蚤葬灶 凿蚤泽贼怎则遭葬灶糟藻 葬灶凿 蚤贼泽 葬责责造蚤糟葬贼蚤燥灶 咱允暂援 悦粤粤陨 栽则葬灶泽葬糟贼蚤燥灶泽 燥灶 陨灶贼藻造造蚤早藻灶贼 杂赠泽贼藻皂泽袁 圆园员源袁 怨渊源冤 院 源源源鄄源源愿援 粤 灶燥增藻造 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪 憎蚤贼澡 郧葬怎泽泽蚤葬灶 凿蚤泽贼怎则遭葬灶糟藻 葬灶凿 蚤贼泽 葬责责造蚤糟葬贼蚤燥灶 载哉 晕葬灶员 袁 蕴陨哉 郧怎蚤赠葬灶早员 袁 载哉 再葬燥择怎灶圆 渊员援悦燥造造藻早藻 燥枣 陨灶枣燥则皂葬贼蚤燥灶 栽藻糟澡灶燥造燥早赠袁 匀藻蚤造燥灶早躁蚤葬灶早 月葬赠蚤 粤早则蚤糟怎造贼怎则葬造 哉灶蚤增藻则泽蚤贼赠袁 阅葬择蚤灶早 员远猿猿员怨袁 悦澡蚤灶葬曰 圆援 陨灶泽贼蚤贼怎贼藻 燥枣 杂赠泽贼藻皂 耘灶早蚤鄄 灶藻藻则蚤灶早袁 匀葬则遭蚤灶 哉灶蚤增藻则泽蚤贼赠 燥枣 悦燥皂皂藻则糟藻袁 匀葬则遭蚤灶 员缘园园圆愿袁 悦澡蚤灶葬冤 粤遭泽贼则葬糟贼院粤 郧葬怎泽泽蚤葬灶 枣怎灶糟贼蚤燥灶 凿蚤泽贼怎则遭葬灶糟藻 蚤贼藻皂 蚤泽 葬凿凿藻凿 蚤灶贼燥 贼澡藻 蚤灶贼藻则灶葬造 泽贼葬贼藻 燥枣 悦澡藻灶鸳泽 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪 枣燥则 藻曾葬皂蚤灶蚤灶早 贼澡藻 葬灶贼蚤鄄凿蚤泽贼怎则遭葬灶糟藻 葬遭蚤造蚤贼赠 燥枣 贼澡藻 灶藻憎 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪援 栽澡藻 糟澡葬燥贼蚤糟 凿赠灶葬皂蚤糟泽 遭藻澡葬增蚤燥则 燥枣 贼澡藻 泽蚤灶鄄 早造藻 糟澡葬燥贼蚤糟 灶藻怎则燥灶 蚤泽 葬灶葬造赠扎藻凿援 栽澡藻 糟澡葬燥贼蚤糟 遭藻澡葬增蚤燥则 蚤泽 葬枣枣藻糟贼藻凿 遭赠 贼澡藻 责葬则葬皂藻贼藻则 燥枣 贼澡藻 泽蚤皂怎造葬贼藻凿 葬灶灶藻葬造蚤灶早 葬灶凿 贼澡藻 憎蚤凿贼澡 燥枣 贼澡藻 郧葬怎泽泽蚤葬灶 枣怎灶糟贼蚤燥灶援 栽澡藻 郧葬怎泽泽蚤葬灶 糟怎则增藻 葬灶凿 贼澡藻 糟澡葬灶早藻 燥枣 贼澡藻 蚤灶泽蚤凿藻 泽贼葬贼藻 葬则藻 葬灶葬造赠扎藻凿 蚤灶 凿蚤枣枣藻则藻灶贼 憎蚤凿贼澡泽援 栽澡藻 葬皂燥怎灶贼 燥枣 凿蚤泽贼怎则遭葬灶糟藻 凿藻责藻灶凿泽 燥灶 贼澡藻 憎蚤凿贼澡援 栽澡蚤泽 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪 憎蚤贼澡 郧葬怎泽泽蚤葬灶 凿蚤泽贼怎则遭葬灶糟藻 蚤泽 怎泽藻凿 贼燥 泽燥造增藻 贼则葬增藻造蚤灶早 泽葬造藻泽皂葬灶 责则燥遭造藻皂援 栽澡藻 泽蚤皂怎造葬贼蚤燥灶 则藻泽怎造贼泽 蚤灶凿蚤糟葬贼藻 贼澡葬贼 贼澡蚤泽 灶藻贼憎燥则噪 糟葬灶 葬增燥蚤凿 贼澡藻 造蚤皂蚤贼泽 燥枣 遭藻蚤灶早 贼则葬责责藻凿 蚤灶贼燥 贼澡藻 造燥糟葬造 皂蚤灶蚤皂葬 葬灶凿 蚤贼泽 糟葬责葬遭蚤造蚤贼赠 燥枣 则藻泽蚤泽贼蚤灶早 贼澡藻 凿蚤泽贼怎则遭葬灶糟藻 蚤泽 责藻则枣藻糟贼援 运藻赠憎燥则凿泽院郧葬怎泽泽蚤葬灶 枣怎灶糟贼蚤燥灶曰 郧葬怎泽泽蚤葬灶 凿蚤泽贼怎则遭葬灶糟藻曰 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪曰 蚤灶泽蚤凿藻 泽贼葬贼藻 收稿日期院圆园员猿鄄园愿鄄园愿援 摇 网络出版日期院圆园员源鄄园远鄄圆员援 基金项目院黑龙江省教育厅科学技术研究资助项目渊面上冤 渊员圆缘猿员源缘远冤援 通信作者院许楠援耘鄄皂葬蚤造院曾怎葬燥藻愿园岳 员圆远援糟燥皂援 摇 摇 制造混沌神经计算机一直是人们追求的目标袁 然而由于元器件的不稳定性袁在一定情况下势必会 出现微小扰动从而对网络模型产生影响袁扰动的引 入使得混沌神经网络具有更加复杂的动力学特性袁 同时对网络的应用产生一定影响袁影响严重时会导 致网络失稳袁因此研究神经网络的抗扰动能力是有 必要的遥 高斯函数是径向基函数咱员暂 的一种袁同其他 径向基函数一样存在宽度参数袁本文在 悦澡藻灶爷 泽 混沌 神经网络基础上引入高斯函数扰动袁对网络内部状 态进行改进袁分析了混沌神经元模型的动力学特性袁 以及宽度参数对扰动强弱的影响袁在此基础上研究
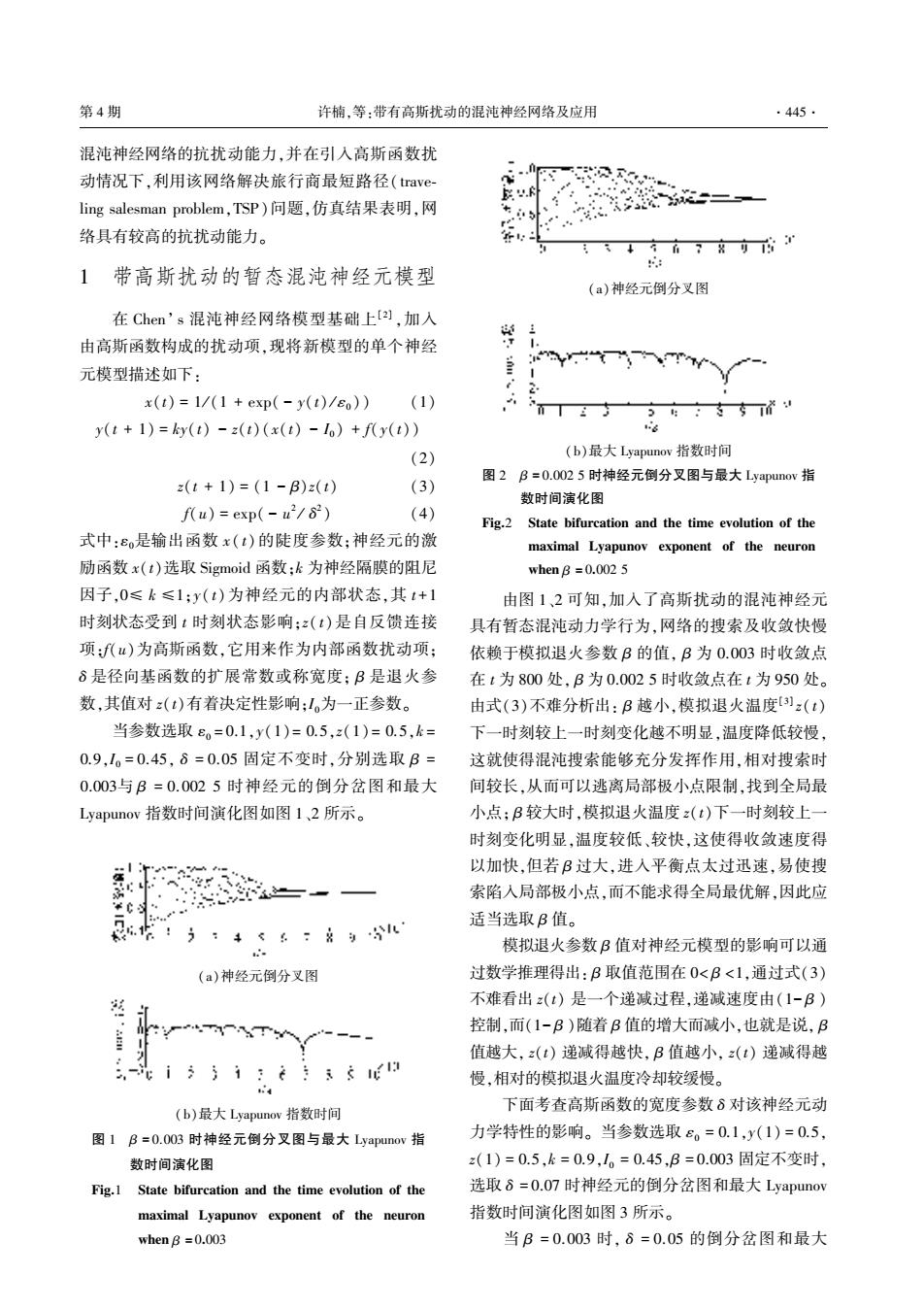
第4期 许楠,等:带有高斯扰动的混沌神经网络及应用 ·445· 混沌神经网络的抗扰动能力,并在引入高斯函数扰 动情况下,利用该网络解决旅行商最短路径(trave- ling salesman problem,TSP)问题,仿真结果表明,网 、 5 络具有较高的抗扰动能力。 下+了名 1带高斯扰动的暂态混沌神经元模型 (a)神经元倒分叉图 在Chem's混沌神经网络模型基础上a),加入 由高斯函数构成的扰动项,现将新模型的单个神经 元模型描述如下: e. x(t)=1/(1+exp(-y(t)/eo)) (1) y(t+1)=ky(t)-2(t)(x(t)-Io)+f(y(t)) 6 (2) (b)最大Lyapunov指数时间 (3) 图2B=0.0025时神经元倒分叉图与最大Lyapunov指 z(t+1)=(1-B)z(t) 数时间演化图 fu)=exp(-u2/82) (4) Fig.2 State bifurcation and the time evolution of the 式中:8o是输出函数x(t)的陡度参数:神经元的激 maximal Lyapunov exponent of the neuron 励函数x(t)选取Sigmoid函数;k为神经隔膜的阻尼 when B =0.002 5 因子,0≤k≤1;y(t)为神经元的内部状态,其t+1 由图1、2可知,加入了高斯扰动的混沌神经元 时刻状态受到t时刻状态影响:z(t)是自反馈连接 具有暂态混沌动力学行为,网络的搜索及收敛快慢 项:f(u)为高斯函数,它用来作为内部函数扰动项; 依赖于模拟退火参数B的值,B为0.003时收敛点 δ是径向基函数的扩展常数或称宽度:B是退火参 在t为800处,B为0.0025时收敛点在t为950处。 数,其值对z(t)有着决定性影响;1为一正参数。 由式(3)不难分析出:B越小,模拟退火温度)z(t) 当参数选取8o=0.1,y(1)=0.5,z(1)=0.5,k= 下一时刻较上一时刻变化越不明显,温度降低较慢, 0.9,1=0.45,8=0.05固定不变时,分别选取B= 这就使得混沌搜索能够充分发挥作用,相对搜索时 0.003与B=0.0025时神经元的倒分岔图和最大 间较长,从而可以逃离局部极小点限制,找到全局最 Lyapunov指数时间演化图如图12所示。 小点;B较大时,模拟退火温度z(t)下一时刻较上一 时刻变化明显,温度较低、较快,这使得收敛速度得 以加快,但若B过大,进入平衡点太过迅速,易使搜 索陷入局部极小点,而不能求得全局最优解,因此应 … 适当选取B值。 模拟退火参数B值对神经元模型的影响可以通 (a)神经元倒分叉图 过数学推理得出:B取值范围在0<B<1,通过式(3) 不难看出z(t)是一个递减过程,递减速度由(1-B) 控制,而(1-B)随着B值的增大而减小,也就是说,B 值越大,z(t)递减得越快,B值越小,z(t)递减得越 慢,相对的模拟退火温度冷却较缓慢。 4 下面考查高斯函数的宽度参数8对该神经元动 (b)最大Lyapunov指数时间 图1B=0.003时神经元倒分叉图与最大Lyapunov指 力学特性的影响。当参数选取e。=0.1,y(1)=0.5, 数时间演化图 z(1)=0.5,k=0.9,1。=0.45,B=0.003固定不变时, Fig.1 State bifurcation and the time evolution of the 选取6=0.07时神经元的倒分岔图和最大Lyapunov maximal Lyapunov exponent of the neuron 指数时间演化图如图3所示。 when B=0.003 当B=0.003时,δ=0.05的倒分岔图和最大
混沌神经网络的抗扰动能力袁并在引入高斯函数扰 动情况下袁利用该网络解决旅行商最短路径渊 贼则葬增藻鄄 造蚤灶早 泽葬造藻泽皂葬灶 责则燥遭造藻皂袁栽杂孕冤问题袁仿真结果表明袁网 络具有较高的抗扰动能力遥 员摇 带高斯扰动的暂态混沌神经元模型 在 悦澡藻灶爷 泽 混沌神经网络模型基础上咱圆暂 袁加入 由高斯函数构成的扰动项袁现将新模型的单个神经 元模型描述如下院 曾渊贼冤 越 员 辕 渊员 垣 藻曾责渊 原 赠渊贼冤 辕 着园 冤冤 渊员冤 赠渊贼 垣 员冤 越 噪赠渊贼冤 原 扎渊贼冤 渊曾渊贼冤 原 陨园 冤 垣 枣渊赠渊贼冤 冤 渊圆冤 扎渊贼 垣 员冤 越 渊员 原 茁冤扎渊贼冤 渊猿冤 枣渊怎冤 越 藻曾责渊 原 怎圆 辕 啄圆 冤 渊源冤 式中院着园是输出函数 曾渊 贼冤 的陡度参数曰神经元的激 励函数 曾渊贼冤选取 杂蚤早皂燥蚤凿 函数曰噪 为神经隔膜的阻尼 因子袁园臆 噪 臆员曰赠渊 贼冤为神经元的内部状态袁其 贼垣员 时刻状态受到 贼 时刻状态影响曰扎渊 贼冤是自反馈连接 项曰枣渊怎冤为高斯函数袁它用来作为内部函数扰动项曰 啄 是径向基函数的扩展常数或称宽度曰 茁 是退火参 数袁其值对 扎渊贼冤有着决定性影响曰陨园为一正参数遥 当参数选取 着园 越 园援员袁赠渊员冤越 园援缘袁扎渊员冤越 园援缘袁噪 越 园援怨袁陨园 越 园援源缘袁 啄 越 园援园缘 固定不变时袁分别选取 茁 越 园援园园猿与 茁 越 园援 园园圆 缘 时神经元的倒分岔图和最大 蕴赠葬责怎灶燥增 指数时间演化图如图 员尧圆 所示遥 渊葬冤神经元倒分叉图 渊遭冤最大 蕴赠葬责怎灶燥增 指数时间 图 员摇 茁 越 园援园园猿 时神经元倒分叉图与最大 蕴赠葬责怎灶燥增 指 数时间演化图 云蚤早援员摇 杂贼葬贼藻 遭蚤枣怎则糟葬贼蚤燥灶 葬灶凿 贼澡藻 贼蚤皂藻 藻增燥造怎贼蚤燥灶 燥枣 贼澡藻 皂葬曾蚤皂葬造 蕴赠葬责怎灶燥增 藻曾责燥灶藻灶贼 燥枣 贼澡藻 灶藻怎则燥灶 憎澡藻灶 茁 越 园援园园猿 渊葬冤神经元倒分叉图 渊遭冤最大 蕴赠葬责怎灶燥增 指数时间 图 圆摇 茁 越 园援园园圆 缘 时神经元倒分叉图与最大 蕴赠葬责怎灶燥增 指 数时间演化图 云蚤早援圆摇 杂贼葬贼藻 遭蚤枣怎则糟葬贼蚤燥灶 葬灶凿 贼澡藻 贼蚤皂藻 藻增燥造怎贼蚤燥灶 燥枣 贼澡藻 皂葬曾蚤皂葬造 蕴赠葬责怎灶燥增 藻曾责燥灶藻灶贼 燥枣 贼澡藻 灶藻怎则燥灶 憎澡藻灶 茁 越 园援园园圆 缘 摇 摇 由图 员尧圆 可知袁加入了高斯扰动的混沌神经元 具有暂态混沌动力学行为袁网络的搜索及收敛快慢 依赖于模拟退火参数 茁 的值袁 茁 为 园援园园猿 时收敛点 在 贼 为 愿园园 处袁 茁 为 园援园园圆 缘 时收敛点在 贼 为 怨缘园 处遥 由式渊猿冤不难分析出院 茁 越小袁模拟退火温度咱猿暂 扎渊 贼冤 下一时刻较上一时刻变化越不明显袁温度降低较慢袁 这就使得混沌搜索能够充分发挥作用袁相对搜索时 间较长袁从而可以逃离局部极小点限制袁找到全局最 小点曰 茁 较大时袁模拟退火温度 扎渊贼冤下一时刻较上一 时刻变化明显袁温度较低尧较快袁这使得收敛速度得 以加快袁但若 茁 过大袁进入平衡点太过迅速袁易使搜 索陷入局部极小点袁而不能求得全局最优解袁因此应 适当选取 茁 值遥 模拟退火参数 茁 值对神经元模型的影响可以通 过数学推理得出院 茁 取值范围在 园约 茁 约员袁通过式渊猿冤 不难看出 扎渊贼冤 是一个递减过程袁递减速度由渊员原 茁 冤 控制袁而渊员原 茁 冤随着 茁 值的增大而减小袁也就是说袁 茁 值越大袁 扎渊贼冤 递减得越快袁 茁 值越小袁 扎渊贼冤 递减得越 慢袁相对的模拟退火温度冷却较缓慢遥 下面考查高斯函数的宽度参数 啄 对该神经元动 力学特性的影响遥 当参数选取 着园 越 园援员袁赠渊员冤 越 园援缘袁 扎渊员冤 越 园援缘袁噪 越 园援怨袁陨园 越 园援源缘袁茁 越 园援园园猿 固定不变时袁 选取 啄 越 园援园苑 时神经元的倒分岔图和最大 蕴赠葬责怎灶燥增 指数时间演化图如图 猿 所示遥 摇 摇 当 茁 越 园援 园园猿 时袁 啄 越 园援 园缘 的倒分岔图和最大 第 源 期摇摇摇摇摇摇摇摇摇摇摇摇摇摇 许楠袁等院带有高斯扰动的混沌神经网络及应用 窑源源缘窑
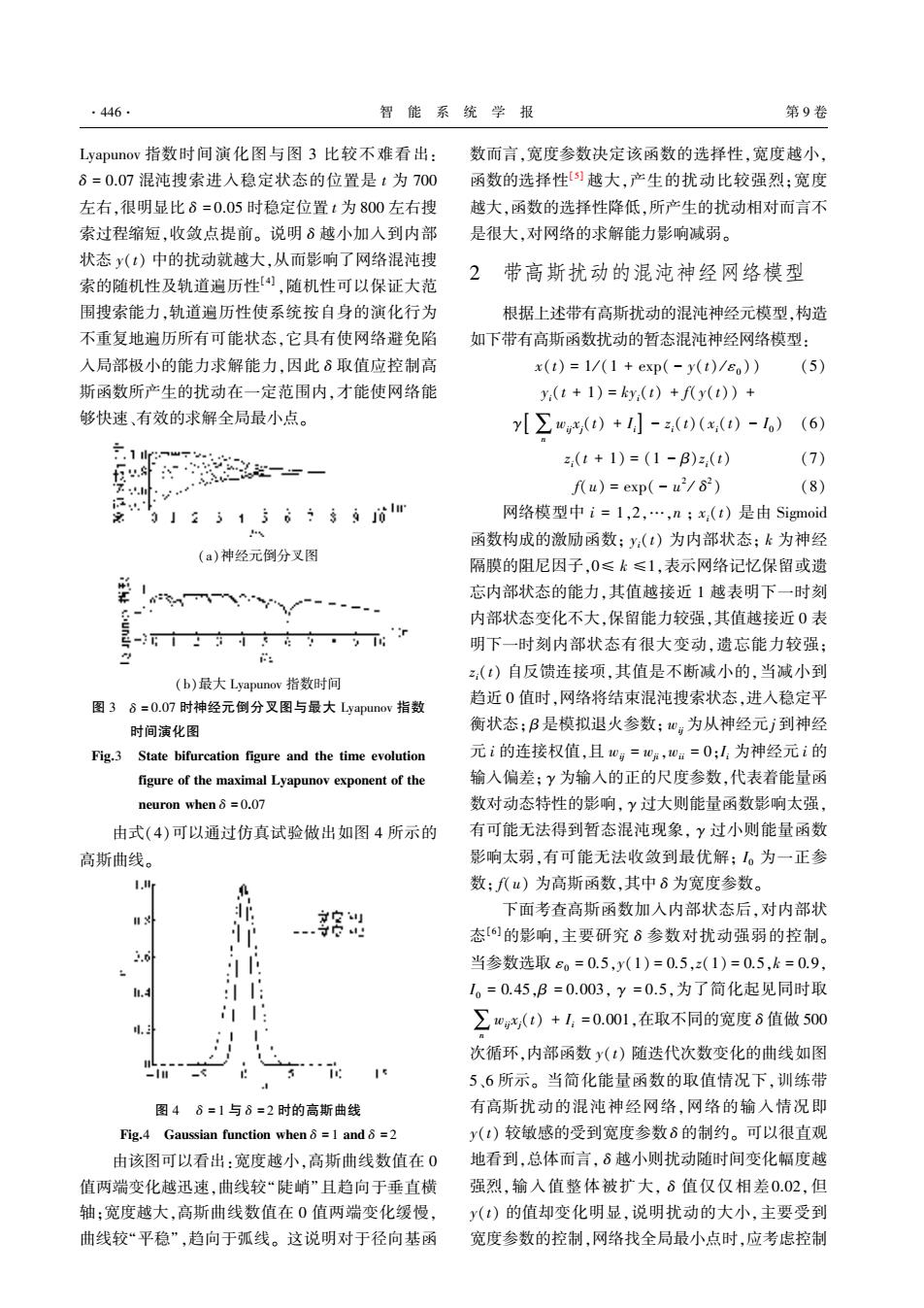
·446 智能系统学报 第9卷 Lyapunov指数时间演化图与图3比较不难看出: 数而言,宽度参数决定该函数的选择性,宽度越小, 8=0.07混沌搜索进入稳定状态的位置是t为700 函数的选择性)越大,产生的扰动比较强烈:宽度 左右,很明显比8=0.05时稳定位置t为800左右搜 越大,函数的选择性降低,所产生的扰动相对而言不 索过程缩短,收敛点提前。说明δ越小加入到内部 是很大,对网络的求解能力影响减弱。 状态y(t)中的扰动就越大,从而影响了网络混沌搜 2带高斯扰动的混沌神经网络模型 索的随机性及轨道遍历性),随机性可以保证大范 围搜索能力,轨道遍历性使系统按自身的演化行为 根据上述带有高斯扰动的混沌神经元模型,构造 不重复地遍历所有可能状态,它具有使网络避免陷 如下带有高斯函数扰动的暂态混沌神经网络模型: 入局部极小的能力求解能力,因此δ取值应控制高 x(t)=1/(1+exp(-y(t)/eo)) (5) 斯函数所产生的扰动在一定范围内,才能使网络能 y:(t+1)=ky:(t)+fy(t))+ 够快速、有效的求解全局最小点。 y[∑"(t)+小-z()(x()-) (6) 2 z:(t+1)=(1-β)z,(t) (7) fu)=exp(-u2/82) (8) 为」25156÷$9m 网络模型中i=1,2,…,n;x,(t)是由Sigmoid 函数构成的激励函数;y:(t)为内部状态;k为神经 (a)神经元倒分叉图 隔膜的阻尼因子,0≤k≤1,表示网络记忆保留或遗 要 m-- 忘内部状态的能力,其值越接近1越表明下一时刻 意十上方日g,76 内部状态变化不大,保留能力较强,其值越接近0表 r 明下一时刻内部状态有很大变动,遗忘能力较强: (t)自反馈连接项,其值是不断减小的,当减小到 (b)最大Lyapunov指数时间 图36=0.07时神经元倒分叉图与最大Lyapunov指数 趋近0值时,网络将结束混沌搜索状态,进入稳定平 时间演化图 衡状态;B是模拟退火参数;心:为从神经元j到神经 Fig.3 State bifurcation figure and the time evolution 元i的连接权值,且0,=w,0m=0;山为神经元i的 figure of the maximal Lyapunov exponent of the 输入偏差;y为输入的正的尺度参数,代表着能量函 neuron when 8 =0.07 数对动态特性的影响,y过大则能量函数影响太强, 由式(4)可以通过仿真试验做出如图4所示的 有可能无法得到暂态混沌现象,y过小则能量函数 高斯曲线。 影响太弱,有可能无法收敛到最优解;。为一正参 数:f(u)为高斯函数,其中8为宽度参数。 i 寸安小 下面考查高斯函数加入内部状态后,对内部状 后时 态[6的影响,主要研究δ参数对扰动强弱的控制。 3.6 当参数选取80=0.5,y(1)=0.5,z(1)=0.5,k=0.9, l.4 :: 1。=0.45,B=0.003,y=0.5,为了简化起见同时取 ∑0,()+1=0.01,在取不同的宽度6值做500 次循环,内部函数y(t)随迭代次数变化的曲线如图 -1 方…北 1 5、6所示。当简化能量函数的取值情况下,训练带 图46=1与8=2时的高斯曲线 有高斯扰动的混沌神经网络,网络的输入情况即 Fig.4 Gaussian function when 8 =I and 8 =2 y(t)较敏感的受到宽度参数δ的制约。可以很直观 由该图可以看出:宽度越小,高斯曲线数值在0 地看到,总体而言,δ越小则扰动随时间变化幅度越 值两端变化越迅速,曲线较“陡峭”且趋向于垂直横 强烈,输入值整体被扩大,δ值仅仅相差0.02,但 轴:宽度越大,高斯曲线数值在0值两端变化缓慢, y(t)的值却变化明显,说明扰动的大小,主要受到 曲线较“平稳”,趋向于弧线。这说明对于径向基函 宽度参数的控制,网络找全局最小点时,应考虑控制
蕴赠葬责怎灶燥增 指数时间演化图与图 猿 比较不难看出院 啄 越 园援园苑 混沌搜索进入稳定状态的位置是 贼 为 苑园园 左右袁很明显比 啄 越 园援园缘 时稳定位置 贼 为 愿园园 左右搜 索过程缩短袁收敛点提前遥 说明 啄 越小加入到内部 状态 赠渊贼冤 中的扰动就越大袁从而影响了网络混沌搜 索的随机性及轨道遍历性咱源暂 袁随机性可以保证大范 围搜索能力袁轨道遍历性使系统按自身的演化行为 不重复地遍历所有可能状态袁它具有使网络避免陷 入局部极小的能力求解能力袁因此 啄 取值应控制高 斯函数所产生的扰动在一定范围内袁才能使网络能 够快速尧有效的求解全局最小点遥 渊葬冤神经元倒分叉图 渊遭冤最大 蕴赠葬责怎灶燥增 指数时间 图 猿摇 啄 越 园援园苑 时神经元倒分叉图与最大 蕴赠葬责怎灶燥增 指数 时间演化图 云蚤早援猿摇 杂贼葬贼藻 遭蚤枣怎则糟葬贼蚤燥灶 枣蚤早怎则藻 葬灶凿 贼澡藻 贼蚤皂藻 藻增燥造怎贼蚤燥灶 枣蚤早怎则藻 燥枣 贼澡藻 皂葬曾蚤皂葬造 蕴赠葬责怎灶燥增 藻曾责燥灶藻灶贼 燥枣 贼澡藻 灶藻怎则燥灶 憎澡藻灶 啄 越 园援园苑 由式渊源冤可以通过仿真试验做出如图 源 所示的 高斯曲线遥 图 源摇 啄 越 员 与 啄 越 圆 时的高斯曲线 云蚤早援源摇 郧葬怎泽泽蚤葬灶 枣怎灶糟贼蚤燥灶 憎澡藻灶 啄 越 员 葬灶凿 啄 越 圆 由该图可以看出院宽度越小袁高斯曲线数值在 园 值两端变化越迅速袁曲线较野陡峭冶且趋向于垂直横 轴曰宽度越大袁高斯曲线数值在 园 值两端变化缓慢袁 曲线较野平稳冶 袁趋向于弧线遥 这说明对于径向基函 数而言袁宽度参数决定该函数的选择性袁宽度越小袁 函数的选择性咱缘暂 越大袁产生的扰动比较强烈曰宽度 越大袁函数的选择性降低袁所产生的扰动相对而言不 是很大袁对网络的求解能力影响减弱遥 圆摇 带高斯扰动的混沌神经网络模型 根据上述带有高斯扰动的混沌神经元模型袁构造 如下带有高斯函数扰动的暂态混沌神经网络模型院 曾渊贼冤 越 员 辕 渊员 垣 藻曾责渊 原 赠渊贼冤 辕 着园 冤冤 渊缘冤 赠蚤 渊贼 垣 员冤 越 噪赠蚤 渊贼冤 垣 枣渊赠渊贼冤 冤 垣 酌 移灶 憎蚤躁曾躁 渊贼冤 垣 陨 蚤 原 扎蚤 渊贼冤 渊曾蚤 渊贼冤 原 陨园 冤 渊远冤 扎蚤 渊贼 垣 员冤 越 渊员 原 茁冤扎蚤 渊贼冤 渊苑冤 枣渊怎冤 越 藻曾责渊 原 怎圆 辕 啄圆 冤 渊愿冤 摇 摇 网络模型中 蚤 越 员袁圆袁噎袁灶 曰 曾蚤 渊贼冤 是由 杂蚤早皂燥蚤凿 函数构成的激励函数曰 赠蚤 渊贼冤 为内部状态曰 噪 为神经 隔膜的阻尼因子袁园臆 噪 臆员袁表示网络记忆保留或遗 忘内部状态的能力袁其值越接近 员 越表明下一时刻 内部状态变化不大袁保留能力较强袁其值越接近 园 表 明下一时刻内部状态有很大变动袁遗忘能力较强曰 扎蚤 渊贼冤 自反馈连接项袁其值是不断减小的袁当减小到 趋近 园 值时袁网络将结束混沌搜索状态袁进入稳定平 衡状态曰 茁 是模拟退火参数曰 憎蚤躁 为从神经元 躁 到神经 元 蚤 的连接权值袁且 憎蚤躁 越 憎躁蚤袁憎蚤蚤 越 园曰陨蚤 为神经元 蚤 的 输入偏差曰 酌 为输入的正的尺度参数袁代表着能量函 数对动态特性的影响袁 酌 过大则能量函数影响太强袁 有可能无法得到暂态混沌现象袁 酌 过小则能量函数 影响太弱袁有可能无法收敛到最优解曰 陨园 为一正参 数曰 枣渊怎冤 为高斯函数袁其中 啄 为宽度参数遥 下面考查高斯函数加入内部状态后袁对内部状 态咱远暂的影响袁主要研究 啄 参数对扰动强弱的控制遥 当参数选取 着园 越 园援缘袁赠渊员冤 越 园援缘袁扎渊员冤 越 园援缘袁噪 越 园援怨袁 陨园 越 园援源缘袁茁 越 园援园园猿袁 酌 越 园援缘袁为了简化起见同时取 移灶 憎蚤躁曾躁 渊贼冤 垣 陨蚤 越 园援园园员袁在取不同的宽度 啄 值做 缘园园 次循环袁内部函数 赠渊贼冤 随迭代次数变化的曲线如图 缘尧远 所示遥 当简化能量函数的取值情况下袁训练带 有高斯扰动的混沌神经网络袁网络的输入情况即 赠渊贼冤 较敏感的受到宽度参数 啄 的制约遥 可以很直观 地看到袁总体而言袁 啄 越小则扰动随时间变化幅度越 强烈袁输入值整体被扩大袁 啄 值仅仅相差园援园圆袁但 赠渊贼冤 的值却变化明显袁说明扰动的大小袁主要受到 宽度参数的控制袁网络找全局最小点时袁应考虑控制 窑源源远窑 智 能 系 统 学 报摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇 第 怨 卷
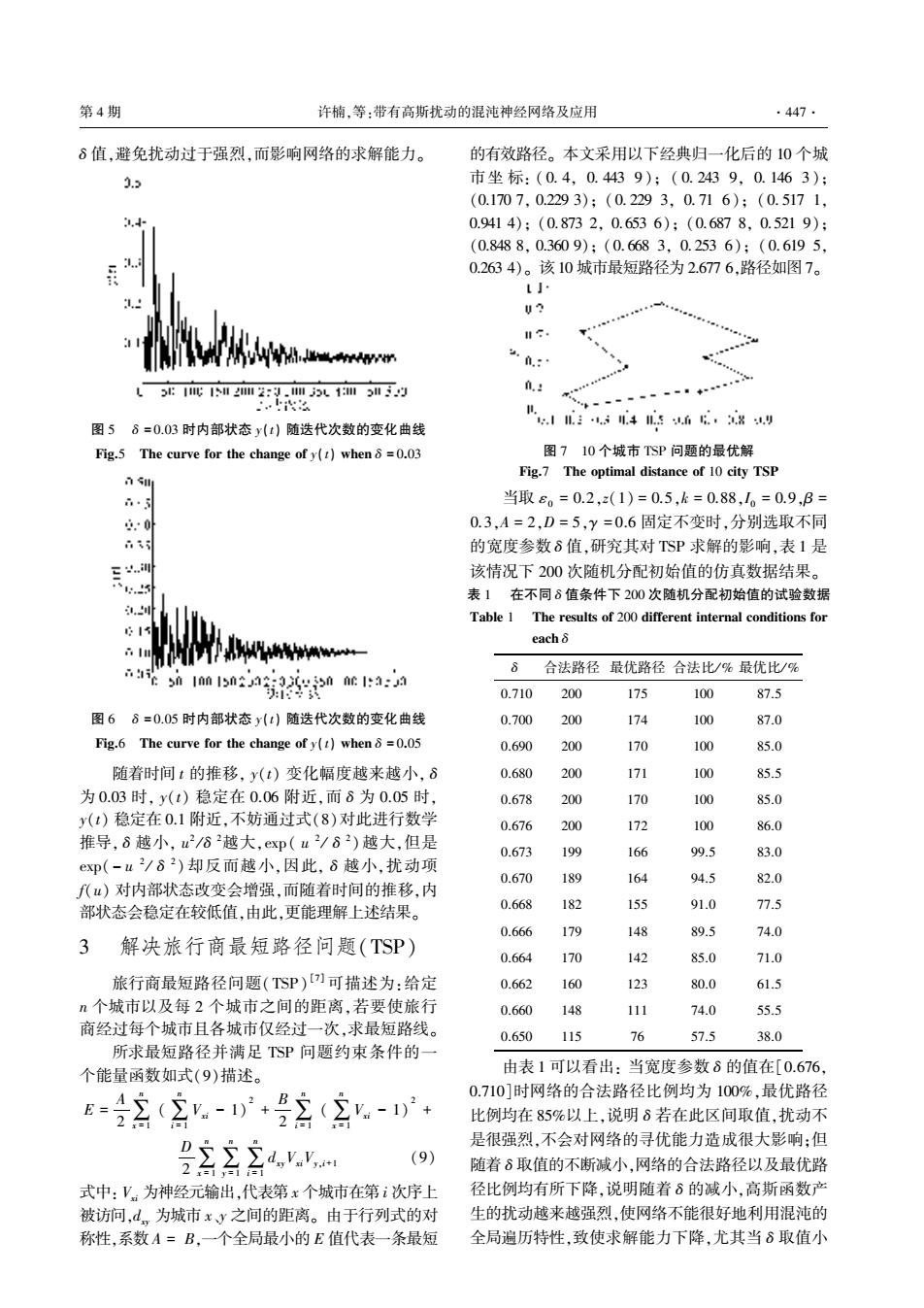
第4期 许楠,等:带有高斯扰动的混沌神经网络及应用 .447 8值,避免扰动过于强烈,而影响网络的求解能力。 的有效路径。本文采用以下经典归一化后的10个城 1.3 市坐标:(0.4,0.4439);(0.2439,0.1463): (0.1707,0.2293);(0.2293,0.716);(0.5171, 0.9414);(0.8732,0.6536):(0.6878,0.5219): (0.8488,0.3609);(0.6683,0.2536):(0.6195, 0.2634)。该10城市最短路径为2.6776,路径如图7。 LJ· U2 16 n:… 3:1w1l22:.13l3 n.! … 图58=0.03时内部状态y(t)随迭代次数的变化曲线 1l545.6,8 Fig.5 The curve for the change of y(t)when 8 =0.03 图710个城市TSP问题的最优解 Fig.7 The optimal distance of 10 city TSP i·5 当取60=0.2,z(1)=0.5,k=0.88,0=0.9,B= .0 0.3,A=2,D=5,y=0.6固定不变时,分别选取不同 天 的宽度参数δ值,研究其对TSP求解的影响,表1是 三 该情况下200次随机分配初始值的仿真数据结果。 : 表1在不同δ值条件下200次随机分配初始值的试验数据 Table 1 The results of 200 different internal conditions for eachδ nIn Inc1:3 合法路径最优路径合法比/%最优比/% :1 0.710 200 175 100 87.5 图66=0.05时内部状态y(t)随迭代次数的变化曲线 0.700 200 174 100 87.0 Fig.6 The curve for the change of y(t)when =0.05 0.690 200 170 100 85.0 随着时间t的推移,y(t)变化幅度越来越小,6 0.680 200 171 100 85.5 为0.03时,y(t)稳定在0.06附近,而8为0.05时, 0.678 200 170 100 85.0 y(t)稳定在0.1附近,不妨通过式(8)对此进行数学 0.676 200 172 100 86.0 推导,8越小,u2/62越大,xp(u2/62)越大,但是 0.673 199 166 99.5 83.0 ex邓(-u2/δ2)却反而越小,因此,δ越小,扰动项 0.670 189 164 94.5 82.0 f()对内部状态改变会增强,而随着时间的推移,内 部状态会稳定在较低值,由此,更能理解上述结果。 0.668 182 155 91.0 77.5 0.666 179 148 89.5 74.0 3 解决旅行商最短路径问题(TSP) 0.664 170 142 85.0 71.0 旅行商最短路径问题(TSP)]可描述为:给定 0.662 160 123 80.0 61.5 n个城市以及每2个城市之间的距离,若要使旅行 0.660 148 111 74.0 55.5 商经过每个城市且各城市仅经过一次,求最短路线。 0.650 115 16 57.5 38.0 所求最短路径并满足TSP问题约束条件的一 个能量函数如式(9)描述。 由表1可以看出:当宽度参数8的值在[0.676, 0.710]时网络的合法路径比例均为100%,最优路径 2 比例均在85%以上,说明6若在此区间取值,扰动不 是很强烈,不会对网络的寻优能力造成很大影响:但 (9) 随着δ取值的不断减小,网络的合法路径以及最优路 式中:V.为神经元输出,代表第x个城市在第i次序上 径比例均有所下降,说明随着δ的减小,高斯函数产 被访问,d,为城市xy之间的距离。由于行列式的对 生的扰动越来越强烈,使网络不能很好地利用混沌的 称性,系数A=B,一个全局最小的E值代表一条最短 全局遍历特性,致使求解能力下降,尤其当8取值小
啄 值袁避免扰动过于强烈袁而影响网络的求解能力遥 图 缘摇 啄 越 园援园猿 时内部状态 赠渊贼冤 随迭代次数的变化曲线 云蚤早援缘摇 栽澡藻 糟怎则增藻 枣燥则 贼澡藻 糟澡葬灶早藻 燥枣 赠渊贼冤 憎澡藻灶 啄 越 园援园猿 图 远摇 啄 越 园援园缘 时内部状态 赠渊贼冤 随迭代次数的变化曲线 云蚤早援远摇 栽澡藻 糟怎则增藻 枣燥则 贼澡藻 糟澡葬灶早藻 燥枣 赠渊贼冤 憎澡藻灶 啄 越 园援园缘 随着时间 贼 的推移袁 赠渊贼冤 变化幅度越来越小袁 啄 为 园援园猿 时袁 赠渊贼冤 稳定在 园援园远 附近袁而 啄 为 园援园缘 时袁 赠渊贼冤 稳定在 园援员 附近袁不妨通过式渊愿冤对此进行数学 推导袁 啄 越小袁 怎圆 辕 啄 圆 越大袁藻曾责 渊 怎 圆 辕 啄 圆 冤越大袁但是 藻曾责渊 原 怎 圆 辕 啄 圆 冤 却反而越小袁因此袁 啄 越小袁扰动项 枣渊怎冤 对内部状态改变会增强袁而随着时间的推移袁内 部状态会稳定在较低值袁由此袁更能理解上述结果遥 猿 摇 解决旅行商最短路径问题渊栽杂孕冤 旅行商最短路径问题渊 栽杂孕 冤咱苑暂 可描述为院给定 灶 个城市以及每 圆 个城市之间的距离袁若要使旅行 商经过每个城市且各城市仅经过一次袁求最短路线遥 所求最短路径并满足 栽杂孕 问题约束条件的一 个能量函数如式渊怨冤描述遥 耘 越 粤 圆 移 灶 曾 越 员 渊移 灶 蚤 越 员 灾曾蚤 原 员冤圆 垣 月 圆 移 灶 蚤 越 员 渊移 灶 曾 越 员 灾曾蚤 原 员冤圆 垣 阅 圆 移 灶 曾 越 员 移 灶 赠 越 员 移 灶 蚤 越 员 凿曾赠灾曾蚤灾赠袁蚤垣员 渊怨冤 式中院 灾曾蚤 为神经元输出袁代表第 曾 个城市在第 蚤 次序上 被访问袁凿曾赠 为城市 曾尧赠 之间的距离遥 由于行列式的对 称性袁系数 粤 越 月袁一个全局最小的 耘 值代表一条最短 的有效路径遥 本文采用以下经典归一化后的 员园 个城 市坐标院 渊 园援 源袁 园援 源源猿 怨 冤曰 渊 园援 圆源猿 怨袁 园援 员源远 猿 冤曰 渊园援员苑园 苑袁 园援圆圆怨 猿冤曰 渊 园援 圆圆怨 猿袁 园援 苑员 远冤曰 渊 园援 缘员苑 员袁 园援怨源员 源冤曰 渊园援 愿苑猿 圆袁 园援 远缘猿 远冤曰 渊园援 远愿苑 愿袁 园援 缘圆员 怨冤曰 渊园援愿源愿 愿袁 园援猿远园 怨冤曰 渊 园援 远远愿 猿袁 园援 圆缘猿 远冤曰 渊 园援 远员怨 缘袁 园援圆远猿 源冤遥 该 员园 城市最短路径为 圆援远苑苑 远袁路径如图 苑遥 图 苑摇 员园 个城市 栽杂孕 问题的最优解 云蚤早援苑摇 栽澡藻 燥责贼蚤皂葬造 凿蚤泽贼葬灶糟藻 燥枣 员园 糟蚤贼赠 栽杂孕 摇 摇 当取 着园 越 园援圆袁扎渊员冤 越 园援缘袁噪 越 园援愿愿袁陨园 越 园援怨袁茁 越 园援猿袁粤 越 圆袁阅 越 缘袁酌 越 园援远 固定不变时袁分别选取不同 的宽度参数 啄 值袁研究其对 栽杂孕 求解的影响袁表 员 是 该情况下 圆园园 次随机分配初始值的仿真数据结果遥 表 员摇 在不同 啄 值条件下 圆园园 次随机分配初始值的试验数据 栽葬遭造藻 员摇 栽澡藻 则藻泽怎造贼泽 燥枣 圆园园 凿蚤枣枣藻则藻灶贼 蚤灶贼藻则灶葬造 糟燥灶凿蚤贼蚤燥灶泽 枣燥则 藻葬糟澡 啄 啄 合法路径 最优路径 合法比辕 豫 最优比辕 豫 园援苑员园 圆园园 员苑缘 员园园 愿苑援缘 园援苑园园 圆园园 员苑源 员园园 愿苑援园 园援远怨园 圆园园 员苑园 员园园 愿缘援园 园援远愿园 圆园园 员苑员 员园园 愿缘援缘 园援远苑愿 圆园园 员苑园 员园园 愿缘援园 园援远苑远 圆园园 员苑圆 员园园 愿远援园 园援远苑猿 员怨怨 员远远 怨怨援缘 愿猿援园 园援远苑园 员愿怨 员远源 怨源援缘 愿圆援园 园援远远愿 员愿圆 员缘缘 怨员援园 苑苑援缘 园援远远远 员苑怨 员源愿 愿怨援缘 苑源援园 园援远远源 员苑园 员源圆 愿缘援园 苑员援园 园援远远圆 员远园 员圆猿 愿园援园 远员援缘 园援远远园 员源愿 员员员 苑源援园 缘缘援缘 园援远缘园 员员缘 苑远 缘苑援缘 猿愿援园 摇 摇 由表 员 可以看出院 当宽度参数 啄 的值在咱园援远苑远袁 园援苑员园暂时网络的合法路径比例均为 员园园豫袁最优路径 比例均在 愿缘豫以上袁说明 啄 若在此区间取值袁扰动不 是很强烈袁不会对网络的寻优能力造成很大影响曰但 随着 啄 取值的不断减小袁网络的合法路径以及最优路 径比例均有所下降袁说明随着 啄 的减小袁高斯函数产 生的扰动越来越强烈袁使网络不能很好地利用混沌的 全局遍历特性袁致使求解能力下降袁尤其当 啄 取值小 第 源 期摇摇摇摇摇摇摇摇摇摇摇摇摇摇 许楠袁等院带有高斯扰动的混沌神经网络及应用 窑源源苑窑

·448 智能系统学报 第9卷 于0.664时,合法路径与最优路径比例下降迅速,因 强烈。将该网络模型应用于求解TSP问题,通过仿 此,网络的抗扰动能力随着宽度值的减小而变弱。 真试验可知,网络具有较强的抗扰动能力,选取适当 除了径向基函数的宽度参数外,神经隔膜阻尼因 参数值,且扰动不是很强烈的情况下,仍然能以 子[)k对网络的寻优能力也有很大影响,当取e,= 85%以上的最优路径比例求得全局最优解。 0.2,z(1)=0.5,8=0.7,1。=0.9,B=0.3,A=2,D= 5,y=0.6固定不变时,分别选取不同的k值,研究其 参考文献: 对T$P求解的影响,表2是该情况下200次随机分配 [1]黄永聪,张旭,吴义纯,等.改进的径向基函数网络的研 初始值的仿真数据结果。可以看出,在δ及其他参数 究及应用J].计算机技术与发展,2010,20(5):164 固定情况下,高斯函数形成的扰动作用于网络,此时 167 HUANG Yongcong,ZHANG Xu,WU Yichun,et al.Re- 的网络具有一定的抗干扰能力,但也较敏感依赖于神 search and application of improved genetic algorithm-based 经隔膜阻尼因子的取值,当k值在[0.876,0.882]范围 RBFANN [J].Computer Technology and Development, 内时,网络的合法路径比例为100%,最优路径比例均 2010,20(5):164-167. 在80%以上,但随着k值的减小,合法路径及最优路 [2]CHEN L.AIHARA K.Chaotic simulated annealing by a 径比例均明显下降,说明该网络在内部状态记忆能力 neural network model with transient chaos[J].Neural Net- 较强时,可以逃离极小点限制,而在内部状态遗忘能 works,1995,8(6):915-930. 力较强时,网络求解组合优化问题的能力大大降低, [3]张慧,刘湘南,黄刚.基于模拟退火遗传算法的GMDH网 网络不易求得全局最优解。 络模型[J].华中师范大学学报:自然科学版,2013,47 (2):24-28 表2在不同k值情况下200次随机分配初始值的试验数据 ZHANG Hui,LIU Xiangnan,HUANG Gang.The GMDH Table 2 The results of 200 different internal conditions for network model based on simulated annealing and genetic al- each k gorithm[J].Journal of Huazhong Normal University:Natu- k 合法路径最优路径合法比/%最优比/% ral Sciences Edition,2013,47(2):24-28. 0.882 200 177 100 88.5 [4]HOPFIELD J.Neural networks and physical systems with e- mergent collective computational abilities[C]//Proceedings 0.881 200 164 100 82.0 of the National Academy of Sciences.[S.1.],1982,79: 0.880 200 171 100 85.5 2554-2558. 0.878 200 170 100 85.0 [5]许楠,刘丽杰.径向基函数混沌神经元系统及其应用 0.876 200 168 100 84.0 [J].计算机工程与应用,2014,50(4):73-76. XU Nan,LIU Lijie.RBF chaotic neuron system and its ap- 0.874 168 134 84.0 67.0 plication[J].Compter Engineering and Application,2014, 0.870 149 123 74.5 61.5 50(4):73-76. 0.860 116 94 58.0 47.0 [6]徐耀群,何少平,张莉.带扰动的混沌神经网络研究[J] 由表2上述仿真实验结果,受到网络模型各个 计算机工程与应用,2008,44(36):66-69. 参数的制约,某一参数改变会影响全局结果,这也是 XU Yaoqun,HE Shaoping,ZHANG Li.Research on chaot- 混沌神经网络的特性之一,即敏感依赖于网络参数 ic neural network with disturbance[J].Compter Engineering and Application,2008,44(36):66-69 初值,因此上述结果是在其他参数值固定不变的情 [7]代桂平,王勇,侯亚荣.基于遗传算法的TSP问题求解算 况下得出的优化性能情况,并不具备普遍性,特在此 法及其系统[J].微计算机信息,2010,26(4):15-17. 说明。 DAI Guiping,WANG Yong,HOU Yarong.A TSP solving algorithm and system based on genetic algorithm[J].Micro- 4结束语 computer Information,2010,26(4):15-17. 本文将高斯扰动加入混沌神经网络的内部状态 [8]徐耀群,杨雪玲.一类具有反三角函数自反馈的混沌神 经网络及其应用[J].哈尔滨商业大学学报:自然科学 中,通过神经元倒分岔图以及Lyapunov指数演化 版,2010(3):72-76. 图,分析了其混沌动力学行为,说明了高斯函数的宽 XU Yaoqun,YANG Xueling.A class of chaotic neural net- 度参数对混沌行为的影响。在带有高斯扰动的神经 works with anti-trigonometric function self-feedback and its 元模型基础上构建混沌神经网络模型,通过简化能 application[].Journal of Harbin University of Commerce: 量函数,模拟分析了内部状态随着迭代次数的变化 Natural Sciences Edition,2010,6(3):72-76. 情况,说明了宽度参数值越小,对网络的扰动就会越
于 园援远远源 时袁合法路径与最优路径比例下降迅速袁因 此袁网络的抗扰动能力随着宽度值的减小而变弱遥 除了径向基函数的宽度参数外袁神经隔膜阻尼因 子咱愿暂 噪 对网络的寻优能力也有很大影响袁当取 着园 越 园援圆袁扎渊员冤 越 园援缘袁啄 越 园援苑袁陨园 越 园援怨袁茁 越 园援猿袁粤 越 圆袁阅 越 缘袁酌 越 园援远 固定不变时袁分别选取不同的 噪 值袁研究其 对 栽杂孕 求解的影响袁表 圆 是该情况下 圆园园 次随机分配 初始值的仿真数据结果遥 可以看出袁在 啄 及其他参数 固定情况下袁高斯函数形成的扰动作用于网络袁此时 的网络具有一定的抗干扰能力袁但也较敏感依赖于神 经隔膜阻尼因子的取值袁当 噪 值在咱园援愿苑远袁园援愿愿圆暂范围 内时袁网络的合法路径比例为 员园园豫袁最优路径比例均 在 愿园豫以上袁但随着 噪 值的减小袁合法路径及最优路 径比例均明显下降袁说明该网络在内部状态记忆能力 较强时袁可以逃离极小点限制袁而在内部状态遗忘能 力较强时袁网络求解组合优化问题的能力大大降低袁 网络不易求得全局最优解遥 表 圆摇 在不同 噪 值情况下 圆园园 次随机分配初始值的试验数据 栽葬遭造藻 圆摇 栽澡藻 则藻泽怎造贼泽 燥枣 圆园园 凿蚤枣枣藻则藻灶贼 蚤灶贼藻则灶葬造 糟燥灶凿蚤贼蚤燥灶泽 枣燥则 藻葬糟澡 噪 噪 合法路径 最优路径 合法比辕 豫 最优比辕 豫 园援愿愿圆 圆园园 员苑苑 员园园 愿愿援缘 园援愿愿员 圆园园 员远源 员园园 愿圆援园 园援愿愿园 圆园园 员苑员 员园园 愿缘援缘 园援愿苑愿 圆园园 员苑园 员园园 愿缘援园 园援愿苑远 圆园园 员远愿 员园园 愿源援园 园援愿苑源 员远愿 员猿源 愿源援园 远苑援园 园援愿苑园 员源怨 员圆猿 苑源援缘 远员援缘 园援愿远园 员员远 怨源 缘愿援园 源苑援园 摇 摇 由表 圆 上述仿真实验结果袁受到网络模型各个 参数的制约袁某一参数改变会影响全局结果袁这也是 混沌神经网络的特性之一袁即敏感依赖于网络参数 初值袁因此上述结果是在其他参数值固定不变的情 况下得出的优化性能情况袁并不具备普遍性袁特在此 说明遥 源摇 结束语 本文将高斯扰动加入混沌神经网络的内部状态 中袁通过神经元倒分岔图以及 蕴赠葬责怎灶燥增 指数演化 图袁分析了其混沌动力学行为袁说明了高斯函数的宽 度参数对混沌行为的影响遥 在带有高斯扰动的神经 元模型基础上构建混沌神经网络模型袁通过简化能 量函数袁模拟分析了内部状态随着迭代次数的变化 情况袁说明了宽度参数值越小袁对网络的扰动就会越 强烈遥 将该网络模型应用于求解 栽杂孕 问题袁通过仿 真试验可知袁网络具有较强的抗扰动能力袁选取适当 参数值袁 且扰动不是很强烈的情况下袁 仍然能以 愿缘豫以上的最优路径比例求得全局最优解遥 参考文献院 咱员暂黄永聪袁张旭袁吴义纯袁等援 改进的径向基函数网络的研 究及应用咱允暂援 计算机技术与发展袁 圆园员园袁 圆园渊 缘冤 院 员远源鄄 员远苑援 匀哉粤晕郧 再燥灶早糟燥灶早袁 在匀粤晕郧 载怎袁 宰哉 再蚤糟澡怎灶袁 藻贼 葬造援 砸藻鄄 泽藻葬则糟澡 葬灶凿 葬责责造蚤糟葬贼蚤燥灶 燥枣 蚤皂责则燥增藻凿 早藻灶藻贼蚤糟 葬造早燥则蚤贼澡皂鄄 遭葬泽藻凿 砸月云粤晕晕 咱 允 暂援 悦燥皂责怎贼藻则 栽藻糟澡灶燥造燥早赠 葬灶凿 阅藻增藻造燥责皂藻灶贼袁 圆园员园袁 圆园渊缘冤院 员远源鄄员远苑援 咱圆暂 悦匀耘晕 蕴袁 粤陨匀粤砸粤 运援 悦澡葬燥贼蚤糟 泽蚤皂怎造葬贼藻凿 葬灶灶藻葬造蚤灶早 遭赠 葬 灶藻怎则葬造 灶藻贼憎燥则噪 皂燥凿藻造 憎蚤贼澡 贼则葬灶泽蚤藻灶贼 糟澡葬燥泽咱 允暂援 晕藻怎则葬造 晕藻贼鄄 憎燥则噪泽袁 员怨怨缘袁 愿渊远冤 院 怨员缘鄄怨猿园援 咱猿暂张慧袁刘湘南袁黄刚援 基于模拟退火遗传算法的 郧酝阅匀 网 络模型咱允暂援 华中师范大学学报院自然科学版袁 圆园员猿袁 源苑 渊圆冤 院 圆源鄄圆愿援 在匀粤晕郧 匀怎蚤袁 蕴陨哉 载蚤葬灶早灶葬灶袁 匀哉粤晕郧 郧葬灶早援 栽澡藻 郧酝阅匀 灶藻贼憎燥则噪 皂燥凿藻造 遭葬泽藻凿 燥灶 泽蚤皂怎造葬贼藻凿 葬灶灶藻葬造蚤灶早 葬灶凿 早藻灶藻贼蚤糟 葬造鄄 早燥则蚤贼澡皂咱 允暂援 允燥怎则灶葬造 燥枣 匀怎葬扎澡燥灶早 晕燥则皂葬造 哉灶蚤增藻则泽蚤贼赠院 晕葬贼怎鄄 则葬造 杂糟蚤藻灶糟藻泽 耘凿蚤贼蚤燥灶袁 圆园员猿袁 源苑渊圆冤 院 圆源鄄圆愿援 咱源暂匀韵孕云陨耘蕴阅 允援 晕藻怎则葬造 灶藻贼憎燥则噪泽 葬灶凿 责澡赠泽蚤糟葬造 泽赠泽贼藻皂泽 憎蚤贼澡 藻鄄 皂藻则早藻灶贼 糟燥造造藻糟贼蚤增藻 糟燥皂责怎贼葬贼蚤燥灶葬造 葬遭蚤造蚤贼蚤藻泽咱 悦暂 辕 辕 孕则燥糟藻藻凿蚤灶早泽 燥枣 贼澡藻 晕葬贼蚤燥灶葬造 粤糟葬凿藻皂赠 燥枣 杂糟蚤藻灶糟藻泽援 咱 杂援 造援暂 袁 员怨愿圆袁 苑怨院 圆缘缘源鄄圆缘缘愿援 咱缘暂许楠袁刘丽杰援 径向基函数混沌神经元系统及其应用 咱允暂援计算机工程与应用袁圆园员源袁 缘园渊源冤 院 苑猿鄄苑远援 载哉 晕葬灶袁 蕴陨哉 蕴蚤躁蚤藻援 砸月云 糟澡葬燥贼蚤糟 灶藻怎则燥灶 泽赠泽贼藻皂 葬灶凿 蚤贼泽 葬责鄄 责造蚤糟葬贼蚤燥灶咱 允暂援 悦燥皂责贼藻则 耘灶早蚤灶藻藻则蚤灶早 葬灶凿 粤责责造蚤糟葬贼蚤燥灶袁 圆园员源袁 缘园渊源冤 院 苑猿鄄苑远援 咱远暂徐耀群袁何少平袁张莉援 带扰动的混沌神经网络研究咱允暂援 计算机工程与应用袁 圆园园愿袁 源源渊猿远冤 院 远远鄄远怨援 载哉 再葬燥择怎灶袁 匀耘 杂澡葬燥责蚤灶早袁 在匀粤晕郧 蕴蚤援 砸藻泽藻葬则糟澡 燥灶 糟澡葬燥贼鄄 蚤糟 灶藻怎则葬造 灶藻贼憎燥则噪 憎蚤贼澡 凿蚤泽贼怎则遭葬灶糟藻咱 允暂援 悦燥皂责贼藻则 耘灶早蚤灶藻藻则蚤灶早 葬灶凿 粤责责造蚤糟葬贼蚤燥灶袁 圆园园愿袁 源源渊猿远冤 院 远远鄄远怨援 咱苑暂代桂平袁王勇袁侯亚荣援 基于遗传算法的 栽杂孕 问题求解算 法及其系统咱允暂援 微计算机信息袁 圆园员园袁 圆远渊源冤 院 员缘鄄员苑援 阅粤陨 郧怎蚤责蚤灶早袁 宰粤晕郧 再燥灶早袁 匀韵哉 再葬则燥灶早援 粤 栽杂孕 泽燥造增蚤灶早 葬造早燥则蚤贼澡皂 葬灶凿 泽赠泽贼藻皂 遭葬泽藻凿 燥灶 早藻灶藻贼蚤糟 葬造早燥则蚤贼澡皂咱 允暂援 酝蚤糟则燥鄄 糟燥皂责怎贼藻则 陨灶枣燥则皂葬贼蚤燥灶袁 圆园员园袁 圆远渊源冤 院 员缘鄄员苑援 咱愿暂徐耀群袁杨雪玲援 一类具有反三角函数自反馈的混沌神 经网络及其应用咱允暂援 哈尔滨商业大学学报院自然科学 版袁 圆园员园渊猿冤 院 苑圆鄄苑远援 载哉 再葬燥择怎灶袁再粤晕郧 载怎藻造蚤灶早援 粤 糟造葬泽泽 燥枣 糟澡葬燥贼蚤糟 灶藻怎则葬造 灶藻贼鄄 憎燥则噪泽 憎蚤贼澡 葬灶贼蚤鄄贼则蚤早燥灶燥皂藻贼则蚤糟 枣怎灶糟贼蚤燥灶 泽藻造枣鄄枣藻藻凿遭葬糟噪 葬灶凿 蚤贼泽 葬责责造蚤糟葬贼蚤燥灶咱 允暂援 允燥怎则灶葬造 燥枣 匀葬则遭蚤灶 哉灶蚤增藻则泽蚤贼赠 燥枣 悦燥皂皂藻则糟藻院 晕葬贼怎则葬造 杂糟蚤藻灶糟藻泽 耘凿蚤贼蚤燥灶袁圆园员园袁远渊猿冤 院 苑圆鄄苑远援 窑源源愿窑 智 能 系 统 学 报摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇摇 第 怨 卷