智能系统：一种基于全局位置估计误差的路标探索策略

第9卷第3期 智能系统学报 Vol.9 No.3 2014年6月 CAAI Transactions on Intelligent Systems Jun.2014 D0:10.3969/j.issn.1673-4785.201310014 网络出版地址：http://www.enki..net/kcms/doi/10.3969/j.issn.16734785.201310014.html 一种基于全局位置估计误差的路标探索策略 马健，俞扬 (南京大学计算机软件新技术国家重点实验室，江苏南京210023) 摘要：自主移动机器人在未知环境中探索和估计路标的方法主要基于SLAM技术。提出一种以全局定位误差最小 化为指导的基于SLAM的探索策略。以全局定位误差的估计为准则，采用Monte Carlo采样来贪心地优化每一步的 行走路径。考虑到SLAM估计的惯性，文中对较大转弯角度进行惩罚，使机器人更倾向于平滑的行走轨迹，从而进一 步提高路标位置的估计精度。文中还将全局定位信息引入SLAM的机器人自身位置估计中，由于全局定位信息历史 运动轨迹，该方法能够有效地校正当机器人移动变化过大时SLAM估计的误差。实验显示了文中方法的有效性。 关键词：SLAM;路标探索；卡尔曼滤波：路径规划：全局误差 中图分类号：TP181文献标志码：A文章编号：1673-4785(2014)03-0313-06 中文引用格式：马健，俞扬.一种基于全局位置估计误差的路标探索策略[J].智能系统学报，2014,9(3)：313-318. 英文引用格式：MA Jian,YU Yang..Landmark exploration strategy using an estimated global localization error[J】.CAAI Transac- tions on Intelligent Systems,2014,9(3):313-318. Landmark exploration strategy using estimated global localization error MA Jian,YU Yang (National Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210023,China) Abstract:Exploration and estimation of landmarks in an unknown environment is an important skill for autonomous robots,most of which are based on the SLAM technique.This paper presents an SLAM based exploration strategy to minimize the global localization error,via greedily optimizing every step by Monte Carlo sampling.Due to the inertia of the SLAM method,we then penalize a large change of direction for a smoother trajectory,which may result in a more accurate estimation of landmarks.To further calibrate the estimation error for a large range of movement,the global localization information is introduced to the procedure of the estimation of the robot,since it depends less on the historical movement trajectory.Experiments verified the effectiveness of the proposed method. Keywords:SLAM;landmark discovery;Kalman filter;path planning;global error 由于自主移动机器人在日常生活服务[】、危险 鉴别和距离的估计，机器人即可计算出自己的所在 环境作业2】、太空探索3]等领域有广泛的应用，对 位置。因此如何有效地在未知环境中探索和估计路 机器人的自主行走和环境感知的研究吸引了越来越 标的位置是自主移动机器人研究的重要问题。 多的研究者关注。路标的发现及其位置的精确估计 在完全未知环境中自主探索和估计路标的方法 自主移动机器人在环境中的定位起到关键作用。当 主要基于同时定位与地图构建(simultaneous locali- 路标的位置信息已知时，通过对视线范围内路标的 zation and mapping,SLAM)技术。SLAM最先由Self 和Cheesemant4]提出，它迭代的通过路标信息修正 收稿日期：2014-03-25.网络出版日期：2014-06-14 自身位置，同时通过自身位置的估计来修正路标信 基金项目：国家自然科学基金面上项目资助项目(61375061)：江苏省自 息，使得在机器人的移动过程中能够逐渐提高其自 然科学基金青年基金资助项目(BK2012303). 通信作者：俞扬yuy@lama.ju.cdu.cn. 身位置和路标的估计精度。由于其重要的理论与应

第 ９ 卷第 ３ 期 智 能 系 统 学 报 Ｖｏｌ．９ №．３ ２０１４ 年 ６ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｊｕｎ． ２０１４ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１３１００１４ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｏｉ ／ １０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３４７８５．２０１３１００１４．ｈｔｍｌ 一种基于全局位置估计误差的路标探索策略 马健，俞扬 （南京大学 计算机软件新技术国家重点实验室，江苏 南京 ２１００２３） 摘 要：自主移动机器人在未知环境中探索和估计路标的方法主要基于 ＳＬＡＭ 技术。 提出一种以全局定位误差最小 化为指导的基于 ＳＬＡＭ 的探索策略。 以全局定位误差的估计为准则，采用 Ｍｏｎｔｅ Ｃａｒｌｏ 采样来贪心地优化每一步的 行走路径。 考虑到 ＳＬＡＭ 估计的惯性，文中对较大转弯角度进行惩罚，使机器人更倾向于平滑的行走轨迹，从而进一 步提高路标位置的估计精度。 文中还将全局定位信息引入 ＳＬＡＭ 的机器人自身位置估计中，由于全局定位信息历史 运动轨迹，该方法能够有效地校正当机器人移动变化过大时 ＳＬＡＭ 估计的误差。 实验显示了文中方法的有效性。 关键词：ＳＬＡＭ；路标探索；卡尔曼滤波；路径规划；全局误差 中图分类号： ＴＰ１８１ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１４）０３⁃０３１３⁃０６ 中文引用格式：马健，俞扬． 一种基于全局位置估计误差的路标探索策略［Ｊ］． 智能系统学报， ２０１４， ９（３）： ３１３⁃３１８． 英文引用格式：ＭＡ Ｊｉａｎ，ＹＵ Ｙａｎｇ． Ｌａｎｄｍａｒｋ ｅｘｐｌｏｒａｔｉｏｎ ｓｔｒａｔｅｇｙ ｕｓｉｎｇ ａｎ ｅｓｔｉｍａｔｅｄ ｇｌｏｂａｌ ｌｏｃａｌｉｚａｔｉｏｎ ｅｒｒｏｒ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃ⁃ ｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１４， ９（３）： ３１３⁃３１８． Ｌａｎｄｍａｒｋ ｅｘｐｌｏｒａｔｉｏｎ ｓｔｒａｔｅｇｙ ｕｓｉｎｇ ｅｓｔｉｍａｔｅｄ ｇｌｏｂａｌ ｌｏｃａｌｉｚａｔｉｏｎ ｅｒｒｏｒ ＭＡ Ｊｉａｎ，ＹＵ Ｙａｎｇ （Ｎａｔｉｏｎａｌ Ｋｅｙ Ｌａｂｏｒａｔｏｒｙ ｆｏｒ Ｎｏｖｅｌ Ｓｏｆｔｗａｒｅ Ｔｅｃｈｎｏｌｏｇｙ， Ｎａｎｊｉｎｇ Ｕｎｉｖｅｒｓｉｔｙ， Ｎａｎｊｉｎｇ ２１００２３， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｅｘｐｌｏｒａｔｉｏｎ ａｎｄ ｅｓｔｉｍａｔｉｏｎ ｏｆ ｌａｎｄｍａｒｋｓ ｉｎ ａｎ ｕｎｋｎｏｗｎ ｅｎｖｉｒｏｎｍｅｎｔ ｉｓ ａｎ ｉｍｐｏｒｔａｎｔ ｓｋｉｌｌ ｆｏｒ ａｕｔｏｎｏｍｏｕｓ ｒｏｂｏｔｓ， ｍｏｓｔ ｏｆ ｗｈｉｃｈ ａｒｅ ｂａｓｅｄ ｏｎ ｔｈｅ ＳＬＡＭ ｔｅｃｈｎｉｑｕｅ． Ｔｈｉｓ ｐａｐｅｒ ｐｒｅｓｅｎｔｓ ａｎ ＳＬＡＭ ｂａｓｅｄ ｅｘｐｌｏｒａｔｉｏｎ ｓｔｒａｔｅｇｙ ｔｏ ｍｉｎｉｍｉｚｅ ｔｈｅ ｇｌｏｂａｌ ｌｏｃａｌｉｚａｔｉｏｎ ｅｒｒｏｒ， ｖｉａ ｇｒｅｅｄｉｌｙ ｏｐｔｉｍｉｚｉｎｇ ｅｖｅｒｙ ｓｔｅｐ ｂｙ Ｍｏｎｔｅ Ｃａｒｌｏ ｓａｍｐｌｉｎｇ． Ｄｕｅ ｔｏ ｔｈｅ ｉｎｅｒｔｉａ ｏｆ ｔｈｅ ＳＬＡＭ ｍｅｔｈｏｄ， ｗｅ ｔｈｅｎ ｐｅｎａｌｉｚｅ ａ ｌａｒｇｅ ｃｈａｎｇｅ ｏｆ ｄｉｒｅｃｔｉｏｎ ｆｏｒ ａ ｓｍｏｏｔｈｅｒ ｔｒａｊｅｃｔｏｒｙ， ｗｈｉｃｈ ｍａｙ ｒｅｓｕｌｔ ｉｎ ａ ｍｏｒｅ ａｃｃｕｒａｔｅ ｅｓｔｉｍａｔｉｏｎ ｏｆ ｌａｎｄｍａｒｋｓ． Ｔｏ ｆｕｒｔｈｅｒ ｃａｌｉｂｒａｔｅ ｔｈｅ ｅｓｔｉｍａｔｉｏｎ ｅｒｒｏｒ ｆｏｒ ａ ｌａｒｇｅ ｒａｎｇｅ ｏｆ ｍｏｖｅｍｅｎｔ， ｔｈｅ ｇｌｏｂａｌ ｌｏｃａｌｉｚａｔｉｏｎ ｉｎｆｏｒｍａｔｉｏｎ ｉｓ ｉｎｔｒｏｄｕｃｅｄ ｔｏ ｔｈｅ ｐｒｏｃｅｄｕｒｅ ｏｆ ｔｈｅ ｅｓｔｉｍａｔｉｏｎ ｏｆ ｔｈｅ ｒｏｂｏｔ， ｓｉｎｃｅ ｉｔ ｄｅｐｅｎｄｓ ｌｅｓｓ ｏｎ ｔｈｅ ｈｉｓｔｏｒｉｃａｌ ｍｏｖｅｍｅｎｔ ｔｒａｊｅｃｔｏｒｙ． Ｅｘｐｅｒｉｍｅｎｔｓ ｖｅｒｉｆｉｅｄ ｔｈｅ ｅｆｆｅｃｔｉｖｅｎｅｓｓ ｏｆ ｔｈｅ ｐｒｏｐｏｓｅｄ ｍｅｔｈｏｄ． Ｋｅｙｗｏｒｄｓ：ＳＬＡＭ； ｌａｎｄｍａｒｋ ｄｉｓｃｏｖｅｒｙ； Ｋａｌｍａｎ ｆｉｌｔｅｒ； ｐａｔｈ ｐｌａｎｎｉｎｇ； ｇｌｏｂａｌ ｅｒｒｏｒ 收稿日期：２０１４⁃０３⁃２５． 网络出版日期：２０１４⁃０６⁃１４． 基金项目：国家自然科学基金面上项目资助项目（６１３７５０６１）；江苏省自 然科学基金青年基金资助项目（ＢＫ２０１２３０３）． 通信作者：俞扬．ｙｕｙ＠ ｌａｍｄａ．ｎｊｕ．ｅｄｕ．ｃｎ． 由于自主移动机器人在日常生活服务［ １ ］ 、危险 环境作业［ ２ ］ 、太空探索［ ３ ］ 等领域有广泛的应用，对 机器人的自主行走和环境感知的研究吸引了越来越 多的研究者关注。 路标的发现及其位置的精确估计 自主移动机器人在环境中的定位起到关键作用。 当 路标的位置信息已知时，通过对视线范围内路标的 鉴别和距离的估计，机器人即可计算出自己的所在 位置。 因此如何有效地在未知环境中探索和估计路 标的位置是自主移动机器人研究的重要问题。 在完全未知环境中自主探索和估计路标的方法 主要基于同时定位与地图构建（ ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉ⁃ ｚａｔｉｏｎ ａｎｄ ｍａｐｐｉｎｇ，ＳＬＡＭ）技术。 ＳＬＡＭ 最先由 Ｓｅｌｆ 和 Ｃｈｅｅｓｅｍａｎ ［ ４ ］提出，它迭代的通过路标信息修正 自身位置，同时通过自身位置的估计来修正路标信 息，使得在机器人的移动过程中能够逐渐提高其自 身位置和路标的估计精度。 由于其重要的理论与应

·314. 智能系统学报 第9卷 用价值，同时定位与地图构建(SLAM)被认为是自 法进行地图构建的主要观点是当机器人路径已知 主移动机器人实现真正自主运动的关键，是智能移 时，确定地图是相对简单的：同样，对于一张给定的 动机器人进入人类日常生活的必要基础，也成为近 地图，确定机器人位姿的概率估计也相对简单。求 年来机器人和人工智能领域中一个非常活跃的研究 解时交替执行2个步骤，分别称为期望步骤(expec- 热点【5刀。 tation step,E步骤)和最大值化步骤(maximization 在以往的研究中，移动机器人在未知环境中游 step,M步骤).在E步骤中，根据当前最大可能性地 走，并在移动过程中使用SLAM技术对路标进行估 图估计各个时间点机器人位置的概率估计，在M步 计[]。常用的游走方式包括随机游走或启发式的 骤中，根据在E步骤所计算得到的位置估计最大可 探索策略，目标是最大限度地、尽快地引导机器人向 能性地图。通过不断重复，机器人位置估计和地图 未探测区域运动，尽量避免在已探测区域内运动，从 估计的精确性不断提高。 而尽快减少未探测的区域。然而，基于SLAM的路 针对EKF-SLAM方法在单峰高斯假设下难以 标估计方法需要机器人重复探测已探测过的环境来 解决数据对应问题、无法构建环行环境地图的缺陷， 提高对自身位置和路标位置的估计精度]，过快移 以及EM-SLAM方法需要多次遍历数据集、难以递 向未探测区域将使得已探测路标的精度过低，导致 增地构建环境地图的缺陷，Hahnel等[s]提出了基于 较大的定位误差。 粒子滤波和卡尔曼滤波的混合SLAM方法，也称为 本文提出一种以全局定位误差最小化为指导的 FastSLAM。FastSLAM算法的基本思想是通过样本 探索策略，进一步提高路标位置的估计精度。本文 集合表示概率密度。每一个样本是关于状态真值的 中还将全局定位信息引入SLAM的位置估计中，有 一个离散猜测，一组样本描述出概率分布的代表性 效地校正当移动变化过大时（例如速度发生变化或 特性。这种基于样本的表示方法使得粒子滤波可以 转弯时)SLAM估计的误差。在模拟环境中的初步 表示各种概率密度，适用于在线的、非线性、非高斯 实验验证了本文方法的有效性。 分布的实时估计。FastSLAM面向路标特征地图，将 机器人位姿估计和地图特征估计相分离，用粒子样 1路径规划相关工作 本描述机器人路径的概率分布，每一个粒子对应于 1.1同时定位与地图构建相关算法 一个可能的机器人路径，每个粒子中维护着一张地 同时定位与地图构建的一个重要支撑技术是概 图，以该粒子所对应的机器人路径为条件，利用扩展 率统计学。以贝叶斯滤波器为基本原理，研究人员 卡尔曼滤波估计地图中各个特征的高斯分布。通过 先后提出了扩展卡尔曼滤波的SLAM算法(EKF- 将粒子滤波和扩展卡尔曼滤波的有机结合， SLAM)[]期望值最大化的SLAM算法(EM FastSLAM极大地减少了粒子需求数[o]。 EKF)[)粒子滤波和扩展卡尔曼滤波的SLAM算法 1.2室内未知环境的路径规划 (FastSLAM)I]等。EKF-SLAM算法是用高斯分布 室内未知环境的路径规划算法可分为3类：1) 表示后验概率的贝叶斯滤波1。该算法作了3个 随机遍历策略，如迂回往复式、内外螺旋式18]：2) 近似。首先，运动模型近似为线性的，在环境为静态 沿边学习加局部路径规划方法，主要应用算法为细 的条件下，地图特征状态不变，仅有机器人状态发生 胞分解法，应用的局部路径规划方法有人工势场法 变化。根据扩展卡尔曼滤波状态方程线性的要求， 完全应激式算法、模糊逻辑算法”)：3)漫步式探测 机器人的非线性运动模型近似为一个带有高斯噪声 路径规划9]，机器人根据自身传感器探测周围环 的线性函数；其次，观测模型近似为线性的。最后， 境信息，并在可视区域根据一定的算法生成局部运 初始的不确定量近似为高斯分布。EKF-SLAM方法 动的规划目标，将机器人的路径规划归结为逐步寻 已被广泛地研究和应用。Dissanayake等u]通过在 找下一步最佳视点的递归。采用此种策略的完全遍 路边架设雷达点路标并人工驾驶室外移动汽车，验 历规划方法有强化学习方法、基于随机树结构的方 证了卡尔曼滤波在同时定位与地图构建方面的有效 法、生物激励的神经网络方法、探测路径规划13]。 性。Castellanos等t)利用扩展卡尔曼滤波研究室内 随机遍历策略有迂回往复式、内外螺旋式、随机转 环境的同时定位与地图构建。悉尼大学的Williams 向式、时间转向式、模板模型法、随机局部遍历的方法。 等]将它应用于水下环境。 这些方法的共同点是：1)不采用现在通用的效益函数：2) EM-SLAM算法是一种由最大似然估计法发展 规划算法简单，方便低成本软硬件设计实现。总的来说， 而来的统计算法，由Thun等[a提出。应用EM算 在不采用效益评价函数，如工作时间、能量损耗、重复覆

用价值，同时定位与地图构建（ ＳＬＡＭ） 被认为是自 主移动机器人实现真正自主运动的关键，是智能移 动机器人进入人类日常生活的必要基础，也成为近 年来机器人和人工智能领域中一个非常活跃的研究 热点［ ５ ⁃ ７ ］ 。 在以往的研究中，移动机器人在未知环境中游 走，并在移动过程中使用 ＳＬＡＭ 技术对路标进行估 计［ ８ ］ 。 常用的游走方式包括随机游走或启发式的 探索策略，目标是最大限度地、尽快地引导机器人向 未探测区域运动，尽量避免在已探测区域内运动，从 而尽快减少未探测的区域。 然而，基于 ＳＬＡＭ 的路 标估计方法需要机器人重复探测已探测过的环境来 提高对自身位置和路标位置的估计精度［ ９ ］ ，过快移 向未探测区域将使得已探测路标的精度过低，导致 较大的定位误差。 本文提出一种以全局定位误差最小化为指导的 探索策略，进一步提高路标位置的估计精度。 本文 中还将全局定位信息引入 ＳＬＡＭ 的位置估计中，有 效地校正当移动变化过大时（例如速度发生变化或 转弯时） ＳＬＡＭ 估计的误差。 在模拟环境中的初步 实验验证了本文方法的有效性。 １ 路径规划相关工作 １．１ 同时定位与地图构建相关算法 同时定位与地图构建的一个重要支撑技术是概 率统计学。 以贝叶斯滤波器为基本原理，研究人员 先后提出了扩展卡尔曼滤波的 ＳＬＡＭ 算法（ ＥＫＦ⁃ ＳＬＡＭ） ［ ７ ］ 期 望 值 最 大 化 的 ＳＬＡＭ 算 法 （ ＥＭ⁃ ＥＫＦ） ［８］粒子滤波和扩展卡尔曼滤波的 ＳＬＡＭ 算法 （ＦａｓｔＳＬＡＭ） ［９］ 等。 ＥＫＦ⁃ＳＬＡＭ 算法是用高斯分布 表示后验概率的贝叶斯滤波［ １０ ］ 。 该算法作了 ３ 个 近似。 首先，运动模型近似为线性的，在环境为静态 的条件下，地图特征状态不变，仅有机器人状态发生 变化。 根据扩展卡尔曼滤波状态方程线性的要求， 机器人的非线性运动模型近似为一个带有高斯噪声 的线性函数；其次，观测模型近似为线性的。 最后， 初始的不确定量近似为高斯分布。 ＥＫＦ⁃ＳＬＡＭ 方法 已被广泛地研究和应用。 Ｄｉｓｓａｎａｙａｋｅ 等［１１］ 通过在 路边架设雷达点路标并人工驾驶室外移动汽车，验 证了卡尔曼滤波在同时定位与地图构建方面的有效 性。 Ｃａｓｔｅｌｌａｎｏｓ 等［１２］利用扩展卡尔曼滤波研究室内 环境的同时定位与地图构建。 悉尼大学的 Ｗｉｌｌｉａｍｓ 等［１３］将它应用于水下环境。 ＥＭ⁃ＳＬＡＭ 算法是一种由最大似然估计法发展 而来的统计算法，由 Ｔｈｒｕｎ 等［１４］ 提出。 应用 ＥＭ 算 法进行地图构建的主要观点是当机器人路径已知 时，确定地图是相对简单的；同样，对于一张给定的 地图，确定机器人位姿的概率估计也相对简单。 求 解时交替执行 ２ 个步骤，分别称为期望步骤（ｅｘｐｅｃ⁃ ｔａｔｉｏｎ ｓｔｅｐ，Ｅ 步骤） 和最大值化步骤（ ｍａｘｉｍｉｚａｔｉｏｎ ｓｔｅｐ，Ｍ 步骤）．在 Ｅ 步骤中，根据当前最大可能性地 图估计各个时间点机器人位置的概率估计，在 Ｍ 步 骤中，根据在 Ｅ 步骤所计算得到的位置估计最大可 能性地图。 通过不断重复，机器人位置估计和地图 估计的精确性不断提高。 针对 ＥＫＦ⁃ＳＬＡＭ 方法在单峰高斯假设下难以 解决数据对应问题、无法构建环行环境地图的缺陷， 以及 ＥＭ⁃ＳＬＡＭ 方法需要多次遍历数据集、难以递 增地构建环境地图的缺陷，Ｈａｈｎｅｌ 等［１５］提出了基于 粒子滤波和卡尔曼滤波的混合 ＳＬＡＭ 方法，也称为 ＦａｓｔＳＬＡＭ。 ＦａｓｔＳＬＡＭ 算法的基本思想是通过样本 集合表示概率密度。 每一个样本是关于状态真值的 一个离散猜测，一组样本描述出概率分布的代表性 特性。 这种基于样本的表示方法使得粒子滤波可以 表示各种概率密度，适用于在线的、非线性、非高斯 分布的实时估计。 ＦａｓｔＳＬＡＭ 面向路标特征地图，将 机器人位姿估计和地图特征估计相分离，用粒子样 本描述机器人路径的概率分布，每一个粒子对应于 一个可能的机器人路径，每个粒子中维护着一张地 图，以该粒子所对应的机器人路径为条件，利用扩展 卡尔曼滤波估计地图中各个特征的高斯分布。 通过 将粒 子 滤 波 和 扩 展 卡 尔 曼 滤 波 的 有 机 结 合， ＦａｓｔＳＬＡＭ 极大地减少了粒子需求数［ １０ ］ 。 １．２ 室内未知环境的路径规划 室内未知环境的路径规划算法可分为 ３ 类：１） 随机遍历策略，如迂回往复式、内外螺旋式［ １８ ］ ；２） 沿边学习加局部路径规划方法，主要应用算法为细 胞分解法，应用的局部路径规划方法有人工势场法、 完全应激式算法、模糊逻辑算法［ １７ ］ ；３）漫步式探测 路径规划［ １９ ］ ，机器人根据自身传感器探测周围环 境信息，并在可视区域根据一定的算法生成局部运 动的规划目标，将机器人的路径规划归结为逐步寻 找下一步最佳视点的递归。 采用此种策略的完全遍 历规划方法有强化学习方法、基于随机树结构的方 法、生物激励的神经网络方法、探测路径规划［ １３ ］ 。 随机遍历策略有迂回往复式、内外螺旋式、随机转 向式、时间转向式、模板模型法、随机局部遍历的方法。 这些方法的共同点是：１）不采用现在通用的效益函数；２） 规划算法简单，方便低成本软硬件设计实现。 总的来说， 在不采用效益评价函数，如工作时间、能量损耗、重复覆 ·３１４· 智 能 系 统 学 报 第 ９ 卷

第3期 马健，等：一种基于全局位置估计误差的路标探索策略 ·315· 盖率等的前提下，可以达到长时间上的大范围覆盖未知 属于漫步式探测路径规划，其目的是最小化全局定 环境。简单的随机遍历策略广泛应用于清洁机器人，如 位误差。机器人从室内某一初始位置出发后先随机 科沃斯地宝系列机器人。迂回往复法也经常作为其他算 游走直至发现一定数量的路标，而后选择下一步的 法的底层策略，或算法判断后所采取的方法[6]。 探测路径。本文的思想是首先选择一组下一步观测 沿边学习加局部路径规划方法中机器人在沿边 视点的候选位置，然后通过效益评价函数评估这些 学习的过程中可以获取室内未知环境的全局信息进 候选位置，选择使效益评价函数最大化的位置作为 行建模，而后采用全局视角和局部路径规划相结合 下一个观测位置。由于在整个可达空间中搜索下一 的方法，遍历整个室内的未知环境。其思想是机器 个最佳探测规划位置意味着巨大的计算量，为减少 人首先沿着未知室内环境边沿行走一周，然后选择 计算量，一般对候选探测位置作一定的约束以提高 某个位置向四周观察，确定合适的探测区域前进，并 计算效率。因此，探测规划研究的讨论主要集中在 以此循环下去，典型的算法有MTCP算法。进行 2个方面，一个是候选位置的生成，另一个是候选位 局部路径规划时，机器人可以建立虚拟子目标，主要 置的评估。 应用算法为细胞分解法，该方法在机器人进行沿边 本文方法将以当前自主移动机器人所在位置为 学习之后，算法将环境分解为多个细胞，每个细胞设 圆心、r为半径的圆上随机生成的N个可达空间内 置一个基点，机器人走遍了基点则完成了遍历。人 的位置作为候选视点，而后分别预估自主移动机器 工势场法、完全应激式算法、模糊逻辑算法以及启发 人在这N个候选位置对应的N条路径上可能观测 式函数也可以作为路径评价的判断标准。 到的新路标的个数及位置、新路标的个数与该条路 虽然沿边学习方法可以获得部分环境信息，但 径预估新探测的环境面积的比例、已经探测的路标 是由于一方面此方法需要对环境进行建模，另一方 个数、已经探测的环境面积的比例。新探测的路标 面传感器信息不完全，因此该方法有局限性。而漫 的位置则用随机的方法进行估计。候选位置的评价 步式路径规划算法则可以避免这些缺点，其方法有 采用效用函数对候选视点进行量化评估，该方法考 强化学习法、基于随机树结构的方法、基于生物激励 虑了全局定位误差最小化，并对较大转弯角度进行 的神经网络方法和探测路径规划方法。 惩罚，以使机器人能够在降低全局定位误差的同时 对于探测路径规划方法，其规划序列为首先选 较为平滑地游走。该效用函数为 择一组下一步观测视点的候选位置，然后通过效用 (punish(a)x 函数评估这些候选位置，选择使效用函数最大化的 位置作为下一个观测视，点。探测路径规划主要包括 ll est_again_location(i)-est_location(i)ll2) 2个方面：候选视点的生成和评价。在机器人进行 (1) 探测时，首先应当考虑的是信息收益和路径成本。 式(1)的目标函数表示全局定位误差，其中i表示需 候选点的生成算法一般为前沿(Frontier)理论、 要估计位置的路标，m表示环境中需要估计位置的 随机生成候选点理论以及这2种方法的混合算法。 路标的个数，α表示机器人一步转弯的角度 前沿理论基本思想是将下一步探测视点放置在已探 est_again_.location(i)表示结合全局位置估计和卡 测环境与未探测环境的交界线上，从而期望获得最 尔曼滤波的SLAM算法得到的第i个路标的估计坐 大化信息收益。随机生成的方法是在传感器扫描区 标，est_location(i)表示上次得到的第i个路标的估 域的圆或者圆环上以随机的方式生成一定数量的候 计坐标，这2个函数的具体估计方法见3.2小节。 选视点。对候选视点的评价中，信息收益是一项重 punish(a)表示转弯角度的惩罚项，本文简单地用 要指标，一般有2种方法进行衡量：一种是直接衡量 机器人转弯时的角度的弧度制大小表示。 传感器探测空间的未知区域的几何信息法：另一种 机器人一步优化路径规划的算法流程如下： 是采用嫡的概率信息法[6]。此外，路径成本也是 1)以预测的机器人所在位置为圆心、R为半径 效益评价函数里的常见参数，如何衡量定位不确定 的圆上随机找N个在面板范围内的点； 性，成为了目前研究的热点。 2)分别预估机器人在这N条路径上会观测到 2 的新路标的个数及位置； 本文方法 3)通过模拟机器人在这N条路径上游走，分别 2.1基于路标的全局位置估计探索策略 计算每条路径对应的效用函数值： 本文提出的室内未知环境机器人路径规划方法 4)选取效用函数值最小路径为下一步探测路径

盖率等的前提下，可以达到长时间上的大范围覆盖未知 环境。 简单的随机遍历策略广泛应用于清洁机器人，如 科沃斯地宝系列机器人。 迂回往复法也经常作为其他算 法的底层策略，或算法判断后所采取的方法［ １６］ 。 沿边学习加局部路径规划方法中机器人在沿边 学习的过程中可以获取室内未知环境的全局信息进 行建模，而后采用全局视角和局部路径规划相结合 的方法，遍历整个室内的未知环境。 其思想是机器 人首先沿着未知室内环境边沿行走一周，然后选择 某个位置向四周观察，确定合适的探测区域前进，并 以此循环下去，典型的算法有 ＭＴＣＰ ［１７］ 算法。 进行 局部路径规划时，机器人可以建立虚拟子目标，主要 应用算法为细胞分解法，该方法在机器人进行沿边 学习之后，算法将环境分解为多个细胞，每个细胞设 置一个基点，机器人走遍了基点则完成了遍历。 人 工势场法、完全应激式算法、模糊逻辑算法以及启发 式函数也可以作为路径评价的判断标准。 虽然沿边学习方法可以获得部分环境信息，但 是由于一方面此方法需要对环境进行建模，另一方 面传感器信息不完全，因此该方法有局限性。 而漫 步式路径规划算法则可以避免这些缺点，其方法有 强化学习法、基于随机树结构的方法、基于生物激励 的神经网络方法和探测路径规划方法。 对于探测路径规划方法，其规划序列为首先选 择一组下一步观测视点的候选位置，然后通过效用 函数评估这些候选位置，选择使效用函数最大化的 位置作为下一个观测视点。 探测路径规划主要包括 ２ 个方面：候选视点的生成和评价。 在机器人进行 探测时，首先应当考虑的是信息收益和路径成本。 候选点的生成算法一般为前沿（Ｆｒｏｎｔｉｅｒ）理论、 随机生成候选点理论以及这 ２ 种方法的混合算法。 前沿理论基本思想是将下一步探测视点放置在已探 测环境与未探测环境的交界线上，从而期望获得最 大化信息收益。 随机生成的方法是在传感器扫描区 域的圆或者圆环上以随机的方式生成一定数量的候 选视点。 对候选视点的评价中，信息收益是一项重 要指标，一般有 ２ 种方法进行衡量：一种是直接衡量 传感器探测空间的未知区域的几何信息法；另一种 是采用熵的概率信息法［ １６ ］ 。 此外，路径成本也是 效益评价函数里的常见参数，如何衡量定位不确定 性，成为了目前研究的热点。 ２ 本文方法 ２．１ 基于路标的全局位置估计探索策略 本文提出的室内未知环境机器人路径规划方法 属于漫步式探测路径规划，其目的是最小化全局定 位误差。 机器人从室内某一初始位置出发后先随机 游走直至发现一定数量的路标，而后选择下一步的 探测路径。 本文的思想是首先选择一组下一步观测 视点的候选位置，然后通过效益评价函数评估这些 候选位置，选择使效益评价函数最大化的位置作为 下一个观测位置。 由于在整个可达空间中搜索下一 个最佳探测规划位置意味着巨大的计算量，为减少 计算量，一般对候选探测位置作一定的约束以提高 计算效率。 因此，探测规划研究的讨论主要集中在 ２ 个方面，一个是候选位置的生成，另一个是候选位 置的评估。 本文方法将以当前自主移动机器人所在位置为 圆心、 ｒ 为半径的圆上随机生成的 Ｎ 个可达空间内 的位置作为候选视点，而后分别预估自主移动机器 人在这 Ｎ 个候选位置对应的 Ｎ 条路径上可能观测 到的新路标的个数及位置、新路标的个数与该条路 径预估新探测的环境面积的比例、已经探测的路标 个数、已经探测的环境面积的比例。 新探测的路标 的位置则用随机的方法进行估计。 候选位置的评价 采用效用函数对候选视点进行量化评估，该方法考 虑了全局定位误差最小化，并对较大转弯角度进行 惩罚，以使机器人能够在降低全局定位误差的同时 较为平滑地游走。 该效用函数为 ｍｉｎ １ ｍ∑ ｍ ｉ ＝ １ （ｐｕｎｉｓｈ（α） × ‖ｅｓｔ＿ａｇａｉｎ＿ｌｏｃａｔｉｏｎ（ｉ）⁃ｅｓｔ＿ｌｏｃａｔｉｏｎ（ｉ）‖２ ） （１） 式（１）的目标函数表示全局定位误差，其中 ｉ 表示需 要估计位置的路标， ｍ 表示环境中需要估计位置的 路标 的 个 数， α 表 示 机 器 人 一 步 转 弯 的 角 度， ｅｓｔ＿ａｇａｉｎ＿ｌｏｃａｔｉｏｎ（ｉ） 表示结合全局位置估计和卡 尔曼滤波的 ＳＬＡＭ 算法得到的第 ｉ 个路标的估计坐 标， ｅｓｔ＿ｌｏｃａｔｉｏｎ（ｉ） 表示上次得到的第 ｉ 个路标的估 计坐标，这 ２ 个函数的具体估计方法见 ３． ２ 小节。 ｐｕｎｉｓｈ（α） 表示转弯角度的惩罚项，本文简单地用 机器人转弯时的角度的弧度制大小表示。 机器人一步优化路径规划的算法流程如下： １）以预测的机器人所在位置为圆心、 Ｒ 为半径 的圆上随机找 Ｎ 个在面板范围内的点； ２）分别预估机器人在这 Ｎ 条路径上会观测到 的新路标的个数及位置； ３）通过模拟机器人在这 Ｎ 条路径上游走，分别 计算每条路径对应的效用函数值； ４）选取效用函数值最小路径为下一步探测路径。 第 ３ 期 马健，等：一种基于全局位置估计误差的路标探索策略 ·３１５·

·316· 智能系统学报 第9卷 2.2全局位置估计和卡尔曼滤波的SLAM算法 选择候选点运动和一步最优规划算法。机器人运动 在传统的SLAM问题的相关的算法中，SLAM 模型为本实验室全方位移动机器人模型，假设其可 是一个滤波问题，是根据系统的初始状态和从0到 以感知半径10m范围内的路标.环境大小为80m× 时刻的观测信息与控制信息估计系统的当前状态。 80m的正方形，其中随机分布了30个路标，游走前 卡尔曼滤波算法就属于这种思想，卡尔曼滤波器已 机器人位于坐标(30m,20m)处，与x轴正方向成 经被广泛认为是实现SLAM的一种基本方法。然 45°夹角，2种游走策略下自主移动机器人运行步数 而，在实际情况中，当移动机器人移动变化过大时 都是1000步。对于本文的方法，在环境中均匀选 (例如速度发生变化或转弯时)，使用传统的SLAM 取100个点，以估计全局误差。 相关算法，机器人的位置和真实的位置的误差会比 3.2实验结果 较大，机器人转弯越急误差可能越大。基于此本文 图1给出了不同探索策略的机器人从相同位置 提出结合全局位置估计和卡尔曼滤波的SLAM算 和角度出发在相等的运行步数下生成的运动路径。 法，由于全局定位信息更少地依赖历史运动轨迹，与 -真实路径 卡尔曼滤波等传统结合使用不仅可以减小机器人游 80r 一随机游走策略下的估计路径 走时的估计误差，而且可以有效降低机器人在转弯 70 时估计的误差。 60 不失一般性，本文假设机器人所在的真实物理 50 位置为(x:y:),i∈{1,2，，n},选取的已观测到 阁 的路标的真实位置为(x,y:),路标的估计位置为 30 (xy),假设需要估计的机器人的位置为(x, 20 y,),优化的目标函数为 10 min∑{[(x,-xa)2+(y,-ya)2]- 2030 4050607080 =1 长/m [(x,-xa)2+(y,-ya)2]} (2) (a)随机游走策略 记机器人与第i个路标的真实距离为 …真实路径 d:=√(x,-xa)+(y-ya) 一本文方法产生的估计路径 80 所以有 70 x2+y2-d= 60 2xx+2y,ya-（x+y) (3) 这样，本文有n个这样的式子，分别将第i个式子减 50 去第n个式子得到n-1个如下的等式： 40 x后+y层-店-x-ya+居= 30 2(xx)x,+2(ysi-y)y, (4) 204 这是一个最小二乘问题，记A为n-1个式(3)的右 10 边部分，即n-1个[2(x-xn)2(y.-ym)],则 1020304050 607080 A为(n-1)×2的矩阵。记x为所求的[x,y,]" 长/m ,B为n-1个式(4)的左边部分，即B为(n-1)× (b)本文方法 1的矩阵。需要估计的机器人的位置的最小二乘的 图1运动轨迹与探索的路标结果对比 最后结果x'=[x,',y,'门T=(A'A)A'B。在机器人 Fig.I The comparison of trajectory and road signs 每一步行走过程中，本文用上述方法得出的估计位 其中，略大的点表示环境中的路标，虚线表示自 置和卡尔曼滤波得出的估计位置的平均值作为机器 主移动机器人真实的游走路线，实线表示自主移动 人最终的估计位置。 机器人分别使用随机游走策略和本文的方法的游走 路线，略小的点表示估计的路标的位置，圆圈表示算 3仿真实验 法预计的路标的估计误差。实验结果表明：1)使用 3.1实验设置 本文的游走策略探测到的路标更多，本文的游走策 本文对2种规划方法做了对比仿真，实验随机 略未探测的路标有6个，而使用随机游走后未探测

２．２ 全局位置估计和卡尔曼滤波的 ＳＬＡＭ 算法 在传统的 ＳＬＡＭ 问题的相关的算法中，ＳＬＡＭ 是一个滤波问题，是根据系统的初始状态和从 ０ 到 ｔ 时刻的观测信息与控制信息估计系统的当前状态。 卡尔曼滤波算法就属于这种思想，卡尔曼滤波器已 经被广泛认为是实现 ＳＬＡＭ 的一种基本方法。 然 而，在实际情况中，当移动机器人移动变化过大时 （例如速度发生变化或转弯时），使用传统的 ＳＬＡＭ 相关算法，机器人的位置和真实的位置的误差会比 较大，机器人转弯越急误差可能越大。 基于此本文 提出结合全局位置估计和卡尔曼滤波的 ＳＬＡＭ 算 法，由于全局定位信息更少地依赖历史运动轨迹，与 卡尔曼滤波等传统结合使用不仅可以减小机器人游 走时的估计误差，而且可以有效降低机器人在转弯 时估计的误差。 不失一般性，本文假设机器人所在的真实物理 位置为 （ｘｉ，ｙｉ） ， ｉ ∈ ｛１，２，．．．，ｎ｝ ，选取的已观测到 的路标的真实位置为 （ｘｔｉ，ｙｔｉ） ，路标的估计位置为 （ｘｓｉ，ｙｓｉ） ，假设需要估计的机器人的位置为 （ｘｓ， ｙｓ） ，优化的目标函数为 ｍｉｎ∑ ｎ ｉ ＝ １ ｛［（ｘｓ － ｘｓｉ） ２ ＋ （ｙｓ － ｙｓｉ） ２ ］ － ［（ｘｔ － ｘｔｉ） ２ ＋ （ｙｔ － ｙｔｉ） ２ ］｝ （２） 记机器人与第 ｉ 个路标的真实距离为 ｄｉ ＝ （ｘｔ － ｘｔｉ） ２ ＋ （ｙｔ － ｙｔｉ） ２ 所以有 ｘ ２ ｓｉ ＋ ｙ ２ ｓｉ － ｄ ２ ｉ ＝ ２ｘｓ ｘｓｉ ＋ ２ｙｓ ｙｓｉ － （ｘ ２ ｓ ＋ ｙ ２ ｓ ） （３） 这样，本文有 ｎ 个这样的式子，分别将第 ｉ 个式子减 去第 ｎ 个式子得到 ｎ － １ 个如下的等式： ｘ ２ ｓｉ ＋ ｙ ２ ｓｉ － ｄ ２ ｉ － ｘ ２ ｓｎ － ｙ ２ ｓｎ ＋ ｄ ２ ｎ ＝ ２（ｘｓｉ － ｘｓｎ ）ｘｓ ＋ ２（ｙｓｉ － ｙｓｎ ）ｙｓ （４） 这是一个最小二乘问题，记 Ａ 为 ｎ － １ 个式（３）的右 边部分，即 ｎ － １ 个 ［２（ｘｓｉ － ｘｓｎ ） ２（ｙｓｉ － ｙｓｎ ）］ ，则 Ａ 为 （ｎ － １） × ２ 的矩阵。 记 ｘ 为所求的 ［ｘｓ ｙｓ］ Ｔ ， Ｂ 为 ｎ － １ 个式（４）的左边部分，即 Ｂ 为 （ｎ － １） × １ 的矩阵。 需要估计的机器人的位置的最小二乘的 最后结果 ｘ′ ＝ ［ｘｓ ′，ｙｓ ′］ Ｔ ＝ （Ａ ＴＡ） －１Ａ ＴＢ 。 在机器人 每一步行走过程中，本文用上述方法得出的估计位 置和卡尔曼滤波得出的估计位置的平均值作为机器 人最终的估计位置。 ３ 仿真实验 ３．１ 实验设置 本文对 ２ 种规划方法做了对比仿真，实验随机 选择候选点运动和一步最优规划算法。 机器人运动 模型为本实验室全方位移动机器人模型，假设其可 以感知半径 １０ ｍ 范围内的路标．环境大小为 ８０ ｍ× ８０ ｍ的正方形，其中随机分布了 ３０ 个路标，游走前 机器人位于坐标（３０ ｍ， ２０ ｍ）处，与 ｘ 轴正方向成 ４５ ｏ 夹角，２ 种游走策略下自主移动机器人运行步数 都是 １ ０００ 步。 对于本文的方法，在环境中均匀选 取 １００ 个点，以估计全局误差。 ３．２ 实验结果 图 １ 给出了不同探索策略的机器人从相同位置 和角度出发在相等的运行步数下生成的运动路径。 （ａ） 随机游走策略 （ｂ） 本文方法 图 １ 运动轨迹与探索的路标结果对比 Ｆｉｇ．１ Ｔｈｅ ｃｏｍｐａｒｉｓｏｎ ｏｆ ｔｒａｊｅｃｔｏｒｙ ａｎｄ ｒｏａｄ ｓｉｇｎｓ 其中，略大的点表示环境中的路标，虚线表示自 主移动机器人真实的游走路线，实线表示自主移动 机器人分别使用随机游走策略和本文的方法的游走 路线，略小的点表示估计的路标的位置，圆圈表示算 法预计的路标的估计误差。 实验结果表明：１）使用 本文的游走策略探测到的路标更多，本文的游走策 略未探测的路标有 ６ 个，而使用随机游走后未探测 ·３１６· 智 能 系 统 学 报 第 ９ 卷

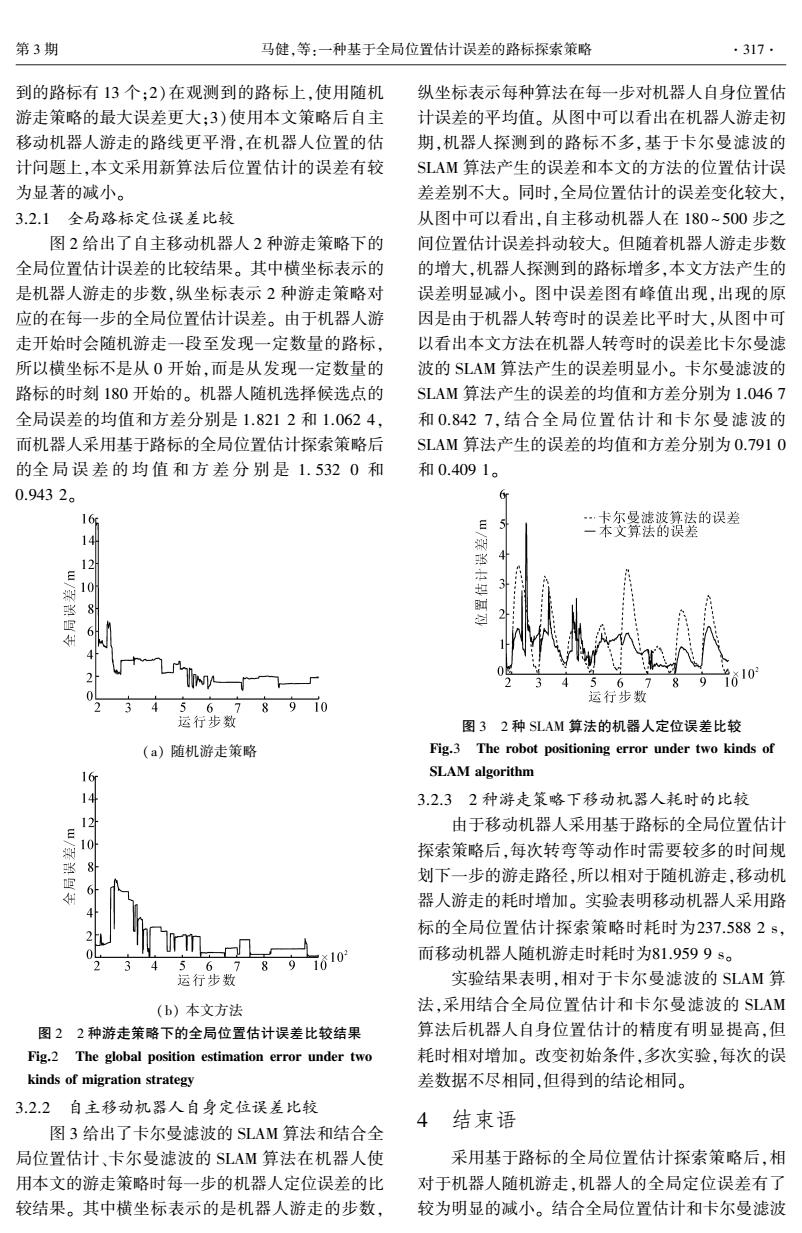
第3期 马健，等：一种基于全局位置估计误差的路标探索策略 .317. 到的路标有13个：2)在观测到的路标上，使用随机 纵坐标表示每种算法在每一步对机器人自身位置估 游走策略的最大误差更大：3)使用本文策略后自主 计误差的平均值。从图中可以看出在机器人游走初 移动机器人游走的路线更平滑，在机器人位置的估 期，机器人探测到的路标不多，基于卡尔曼滤波的 计问题上，本文采用新算法后位置估计的误差有较 SLAM算法产生的误差和本文的方法的位置估计误 为显著的减小。 差差别不大。同时，全局位置估计的误差变化较大， 3.2.1全局路标定位误差比较 从图中可以看出，自主移动机器人在180~500步之 图2给出了自主移动机器人2种游走策略下的 间位置估计误差抖动较大。但随着机器人游走步数 全局位置估计误差的比较结果。其中横坐标表示的 的增大，机器人探测到的路标增多，本文方法产生的 是机器人游走的步数，纵坐标表示2种游走策略对 误差明显减小。图中误差图有峰值出现，出现的原 应的在每一步的全局位置估计误差。由于机器人游 因是由于机器人转弯时的误差比平时大，从图中可 走开始时会随机游走一段至发现一定数量的路标， 以看出本文方法在机器人转弯时的误差比卡尔曼滤 所以横坐标不是从0开始，而是从发现一定数量的 波的SLAM算法产生的误差明显小。卡尔曼滤波的 路标的时刻180开始的。机器人随机选择候选点的 SLAM算法产生的误差的均值和方差分别为1.0467 全局误差的均值和方差分别是1.8212和1.0624， 和0.8427，结合全局位置估计和卡尔曼滤波的 而机器人采用基于路标的全局位置估计探索策略后 SLAM算法产生的误差的均值和方差分别为0.7910 的全局误差的均值和方差分别是1.5320和 和0.4091。 0.9432。 ,卡尔曼滤波算法的误差 1 一本文算法的误差 12 10 3 细 6 2 56 9 0 运行步数 4 5678910 运行步数 图32种SLAM算法的机器人定位误差比较 (a)随机游走策略 Fig.3 The robot positioning error under two kinds of SLAM algorithm 14 3.2.32种游走策略下移动机器人耗时的比较 208 由于移动机器人采用基于路标的全局位置估计 探索策略后，每次转弯等动作时需要较多的时间规 划下一步的游走路径，所以相对于随机游走，移动机 6 器人游走的耗时增加。实验表明移动机器人采用路 标的全局位置估计探索策略时耗时为237.5882s, 36789六610 而移动机器人随机游走时耗时为81.9599s。 运行步数 实验结果表明，相对于卡尔曼滤波的SLAM算 (b)本文方法 法，采用结合全局位置估计和卡尔曼滤波的SLAM 图22种游走策略下的全局位置估计误差比较结果 算法后机器人自身位置估计的精度有明显提高，但 Fig.2 The global position estimation error under two 耗时相对增加。改变初始条件，多次实验，每次的误 kinds of migration strategy 差数据不尽相同，但得到的结论相同。 3.2.2自主移动机器人自身定位误差比较 4结束语 图3给出了卡尔曼滤波的SLAM算法和结合全 局位置估计、卡尔曼滤波的SLAM算法在机器人使 采用基于路标的全局位置估计探索策略后，相 用本文的游走策略时每一步的机器人定位误差的比 对于机器人随机游走，机器人的全局定位误差有了 较结果。其中横坐标表示的是机器人游走的步数， 较为明显的减小。结合全局位置估计和卡尔曼滤波

到的路标有 １３ 个；２）在观测到的路标上，使用随机 游走策略的最大误差更大；３）使用本文策略后自主 移动机器人游走的路线更平滑，在机器人位置的估 计问题上，本文采用新算法后位置估计的误差有较 为显著的减小。 ３．２．１ 全局路标定位误差比较 图 ２ 给出了自主移动机器人 ２ 种游走策略下的 全局位置估计误差的比较结果。 其中横坐标表示的 是机器人游走的步数，纵坐标表示 ２ 种游走策略对 应的在每一步的全局位置估计误差。 由于机器人游 走开始时会随机游走一段至发现一定数量的路标， 所以横坐标不是从 ０ 开始，而是从发现一定数量的 路标的时刻 １８０ 开始的。 机器人随机选择候选点的 全局误差的均值和方差分别是 １．８２１ ２ 和 １．０６２ ４， 而机器人采用基于路标的全局位置估计探索策略后 的全 局 误 差 的 均 值 和 方 差 分 别 是 １． ５３２ ０ 和 ０．９４３ ２。 （ａ） 随机游走策略 （ｂ） 本文方法 图 ２ ２ 种游走策略下的全局位置估计误差比较结果 Ｆｉｇ．２ Ｔｈｅ ｇｌｏｂａｌ ｐｏｓｉｔｉｏｎ ｅｓｔｉｍａｔｉｏｎ ｅｒｒｏｒ ｕｎｄｅｒ ｔｗｏ ｋｉｎｄｓ ｏｆ ｍｉｇｒａｔｉｏｎ ｓｔｒａｔｅｇｙ ３．２．２ 自主移动机器人自身定位误差比较 图 ３ 给出了卡尔曼滤波的 ＳＬＡＭ 算法和结合全 局位置估计、卡尔曼滤波的 ＳＬＡＭ 算法在机器人使 用本文的游走策略时每一步的机器人定位误差的比 较结果。 其中横坐标表示的是机器人游走的步数， 纵坐标表示每种算法在每一步对机器人自身位置估 计误差的平均值。 从图中可以看出在机器人游走初 期，机器人探测到的路标不多，基于卡尔曼滤波的 ＳＬＡＭ 算法产生的误差和本文的方法的位置估计误 差差别不大。 同时，全局位置估计的误差变化较大， 从图中可以看出，自主移动机器人在 １８０ ～ ５００ 步之 间位置估计误差抖动较大。 但随着机器人游走步数 的增大，机器人探测到的路标增多，本文方法产生的 误差明显减小。 图中误差图有峰值出现，出现的原 因是由于机器人转弯时的误差比平时大，从图中可 以看出本文方法在机器人转弯时的误差比卡尔曼滤 波的 ＳＬＡＭ 算法产生的误差明显小。 卡尔曼滤波的 ＳＬＡＭ 算法产生的误差的均值和方差分别为 １．０４６ ７ 和 ０．８４２ ７， 结合全局位置估计和卡尔曼滤波的 ＳＬＡＭ 算法产生的误差的均值和方差分别为 ０．７９１ ０ 和 ０．４０９ １。 图 ３ ２ 种 ＳＬＡＭ 算法的机器人定位误差比较 Ｆｉｇ．３ Ｔｈｅ ｒｏｂｏｔ ｐｏｓｉｔｉｏｎｉｎｇ ｅｒｒｏｒ ｕｎｄｅｒ ｔｗｏ ｋｉｎｄｓ ｏｆ ＳＬＡＭ ａｌｇｏｒｉｔｈｍ ３．２．３ ２ 种游走策略下移动机器人耗时的比较 由于移动机器人采用基于路标的全局位置估计 探索策略后，每次转弯等动作时需要较多的时间规 划下一步的游走路径，所以相对于随机游走，移动机 器人游走的耗时增加。 实验表明移动机器人采用路 标的全局位置估计探索策略时耗时为２３７．５８８ ２ ｓ， 而移动机器人随机游走时耗时为８１．９５９ ９ ｓ。 实验结果表明，相对于卡尔曼滤波的 ＳＬＡＭ 算 法，采用结合全局位置估计和卡尔曼滤波的 ＳＬＡＭ 算法后机器人自身位置估计的精度有明显提高，但 耗时相对增加。 改变初始条件，多次实验，每次的误 差数据不尽相同，但得到的结论相同。 ４ 结束语 采用基于路标的全局位置估计探索策略后，相 对于机器人随机游走，机器人的全局定位误差有了 较为明显的减小。 结合全局位置估计和卡尔曼滤波 第 ３ 期 马健，等：一种基于全局位置估计误差的路标探索策略 ·３１７·

.318. 智能系统学报 第9卷 的SLAM算法相对于基于卡尔曼滤波的SLAM算 [11]DISSANAYAKE M W M G,NEWMAN P,CLARK S,et 法，可以有效地减小机器人位置的估计误差。更多 al.A solution to the simultaneous localization and map 的实验分析以及机器人多步优化路径规划问题等， building (SLAM)problem[J].IEEE Transactions on Ro- 值得进一步研究。 botics and Automation,2001,17(3):229-241. [12]CASTELLANOS J A,MONTIEL J MM,NEIRA J,et al. 参考文献： The SPmap:A probabilistic framework for simultaneous lo- calization and map building[J].IEEE Transactions on Ro- [1]DURRANT-WHYTE H F.An autonomous guided vehicle for botics and Automation,1999.15(5):948-952. cargo handling applications[J].International Journal of Ro- [13]WILLIAMS S,DISSANAYAKE G,DURRANT-WHYTE H botics Research,1996,15(5):407-440. F.Towards terrain-aided navigation for underwater robotics [2]MONTEMERLO M,PINEAU J,ROY N,et al.Experiences [J].Advanced Robotics,2001,15(5):533-549. with a mobile robotic guide for the elderly[C]//Proceedings [14 THRUN S.Probabilistic algorithms in robotics J].Al of the 18th National Conference on Artificial Intelligence. Magazine,2000.21(4):93-109. Edmonton,Canada.2002:587-592. [15]HAHNEL D,BURGARD W,FOX D,et al.An efficient [3]HUNTSBERGER T,AGHAZARIAN H,CHENG Y,et al. FastSLAM algorithm for generating maps of large-scale cy- Rover autonomy for long range navigation and science data clic environments from raw laser range measurements acquisition on planetary surfaces[C]//Proceedings of IEEE [C]//Proceedings of 2003 IEEE/RSJ International Con- International Conference on Robotics and Automation. ference on Intelligent Robots and Systems.Las Vegas, Washington,.DC,2002:3161-3168. NV,2003:206-211. [4]SMITH R,SELF M,Cheeseman P.Estimating uncertain [16]李一波，张庆涛.室内未知环境遍历路径规划算法综述 spatial relationships in robotics[M].Autonomous Robot Ve- [J].计算机科学，2012,39(11A):334-338. hicles,1990:167-193. LI Yibo,ZHANG Qingtao.Review of coverage path planning [5]LI C,HUANG Y,KANG Y,et al.Monocular SLAM using arithmetic in unknown indoor environment[J].Computer vertical straight lines with inverse-depth representation Science,2012,39(11A):334-338. [C]//Proceedings of 7th IEEE World Congress on Intelli- [17]ULRICH I,MONDADA F,NICOUD J D.Autonomous gent Control and Automation.Chongqing,China,2008: vacuum cleaner J.Robotics and Autonomous Systems, 3015-3020. 1997,19(3):233-245. [6]THRUN S,BURGARD W,FOX D.A probabilistic ap- [18]OH JS,PARK J B,CHOI Y H.Complete coverage navi- proach to concurrent mapping and localization for mobile ro- gation of clean robot based on triangular cell map[J]. bots[J.Autonomous Robots,1998,5(3/4):253-271. IEEE Transactions on Industrial Electronics,2004,51 [7]GRISETTI G,STACHNISS C,BURGARD W.Improved (3):718-726. techniques for grid mapping with Rao-Blackwellized particle [19]JEBARI I,BAZEILLE S,FILLIAT D.Informatics in con- filters[J].IEEE Transactions on Robotics,2007,23(1): trol,automation and robotics M ]Berlin:Springer, 34-46. 2012:224-237 [8]张恒，樊晓平.移动机器人同步定位与地图构建过程中 作者简介： 的轨迹规划研究[J].机器人，2006,28(3)：285-290. 马健，1990年生，男，硕士研究生， ZHANG Heng,FAN Xiaoping.Mobile robot trajectory plan- 主要研究方向为演化计算、强化学习。 ning in simultaneous localization and mapping problem[] Robot,2006,28(3):285-290. [9]NEWMAN P.On the structure and solution of the simultane- ous localisation and map building problem[D].Sydney:U. niversity of Sydney,1999:1-5. [10]熊蓉.室内未知环境线段特征地图构建[D].杭州：浙 俞扬，1982年生，男，助理研究员， 江大学，2009：10-23. 博士，主要研究方向为人工智能、机器 XIONG Rong.Line feature map building for unknown indoor 学习、演化计算、强化学习，发表学术论 environments D].Hangzhou:Zhejiang University,2009: 文20余篇。 10-23

的 ＳＬＡＭ 算法相对于基于卡尔曼滤波的 ＳＬＡＭ 算 法，可以有效地减小机器人位置的估计误差。 更多 的实验分析以及机器人多步优化路径规划问题等， 值得进一步研究。 参考文献： ［１］ＤＵＲＲＡＮＴ⁃ＷＨＹＴＥ Ｈ Ｆ． Ａｎ ａｕｔｏｎｏｍｏｕｓ ｇｕｉｄｅｄ ｖｅｈｉｃｌｅ ｆｏｒ ｃａｒｇｏ ｈａｎｄｌｉｎｇ ａｐｐｌｉｃａｔｉｏｎｓ［Ｊ］． Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｊｏｕｒｎａｌ ｏｆ Ｒｏ⁃ ｂｏｔｉｃｓ Ｒｅｓｅａｒｃｈ， １９９６， １５（５）： ４０７⁃４４０． ［２］ＭＯＮＴＥＭＥＲＬＯ Ｍ， ＰＩＮＥＡＵ Ｊ， ＲＯＹ Ｎ， ｅｔ ａｌ． Ｅｘｐｅｒｉｅｎｃｅｓ ｗｉｔｈ ａ ｍｏｂｉｌｅ ｒｏｂｏｔｉｃ ｇｕｉｄｅ ｆｏｒ ｔｈｅ ｅｌｄｅｒｌｙ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ １８ｔｈ Ｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ａｒｔｉｆｉｃｉａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ． Ｅｄｍｏｎｔｏｎ， Ｃａｎａｄａ． ２００２： ５８７⁃５９２． ［３］ＨＵＮＴＳＢＥＲＧＥＲ Ｔ， ＡＧＨＡＺＡＲＩＡＮ Ｈ， ＣＨＥＮＧ Ｙ， ｅｔ ａｌ． Ｒｏｖｅｒ ａｕｔｏｎｏｍｙ ｆｏｒ ｌｏｎｇ ｒａｎｇｅ ｎａｖｉｇａｔｉｏｎ ａｎｄ ｓｃｉｅｎｃｅ ｄａｔａ ａｃｑｕｉｓｉｔｉｏｎ ｏｎ ｐｌａｎｅｔａｒｙ ｓｕｒｆａｃｅｓ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｒｏｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｍａｔｉｏｎ． Ｗａｓｈｉｎｇｔｏｎ， ＤＣ， ２００２： ３１６１⁃３１６８． ［４］ ＳＭＩＴＨ Ｒ， ＳＥＬＦ Ｍ， Ｃｈｅｅｓｅｍａｎ Ｐ． Ｅｓｔｉｍａｔｉｎｇ ｕｎｃｅｒｔａｉｎ ｓｐａｔｉａｌ ｒｅｌａｔｉｏｎｓｈｉｐｓ ｉｎ ｒｏｂｏｔｉｃｓ［Ｍ］． Ａｕｔｏｎｏｍｏｕｓ Ｒｏｂｏｔ Ｖｅ⁃ ｈｉｃｌｅｓ， １９９０： １６７⁃１９３． ［５］ＬＩ Ｃ， ＨＵＡＮＧ Ｙ， ＫＡＮＧ Ｙ， ｅｔ ａｌ． Ｍｏｎｏｃｕｌａｒ ＳＬＡＭ ｕｓｉｎｇ ｖｅｒｔｉｃａｌ ｓｔｒａｉｇｈｔ ｌｉｎｅｓ ｗｉｔｈ ｉｎｖｅｒｓｅ⁃ｄｅｐｔｈ ｒｅｐｒｅｓｅｎｔａｔｉｏｎ ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ７ｔｈ ＩＥＥＥ Ｗｏｒｌｄ Ｃｏｎｇｒｅｓｓ ｏｎ Ｉｎｔｅｌｌｉ⁃ ｇｅｎｔ Ｃｏｎｔｒｏｌ ａｎｄ Ａｕｔｏｍａｔｉｏｎ． Ｃｈｏｎｇｑｉｎｇ， Ｃｈｉｎａ， ２００８： ３０１５⁃３０２０． ［６］ ＴＨＲＵＮ Ｓ， ＢＵＲＧＡＲＤ Ｗ， ＦＯＸ Ｄ． Ａ ｐｒｏｂａｂｉｌｉｓｔｉｃ ａｐ⁃ ｐｒｏａｃｈ ｔｏ ｃｏｎｃｕｒｒｅｎｔ ｍａｐｐｉｎｇ ａｎｄ ｌｏｃａｌｉｚａｔｉｏｎ ｆｏｒ ｍｏｂｉｌｅ ｒｏ⁃ ｂｏｔｓ［Ｊ］． Ａｕｔｏｎｏｍｏｕｓ Ｒｏｂｏｔｓ， １９９８， ５（３ ／ ４）： ２５３⁃２７１． ［７］ ＧＲＩＳＥＴＴＩ Ｇ， ＳＴＡＣＨＮＩＳＳ Ｃ， ＢＵＲＧＡＲＤ Ｗ． Ｉｍｐｒｏｖｅｄ ｔｅｃｈｎｉｑｕｅｓ ｆｏｒ ｇｒｉｄ ｍａｐｐｉｎｇ ｗｉｔｈ Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｚｅｄ ｐａｒｔｉｃｌｅ ｆｉｌｔｅｒｓ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｒｏｂｏｔｉｃｓ， ２００７， ２３（１）： ３４⁃４６． ［８］张恒， 樊晓平． 移动机器人同步定位与地图构建过程中 的轨迹规划研究［Ｊ］． 机器人， ２００６， ２８（３）： ２８５⁃２９０． ＺＨＡＮＧ Ｈｅｎｇ， ＦＡＮ Ｘｉａｏｐｉｎｇ． Ｍｏｂｉｌｅ ｒｏｂｏｔ ｔｒａｊｅｃｔｏｒｙ ｐｌａｎ⁃ ｎｉｎｇ ｉｎ ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐｐｉｎｇ ｐｒｏｂｌｅｍ［ Ｊ］． Ｒｏｂｏｔ， ２００６， ２８（３）： ２８５⁃２９０． ［９］ＮＥＷＭＡＮ Ｐ． Ｏｎ ｔｈｅ ｓｔｒｕｃｔｕｒｅ ａｎｄ ｓｏｌｕｔｉｏｎ ｏｆ ｔｈｅ ｓｉｍｕｌｔａｎｅ⁃ ｏｕｓ ｌｏｃａｌｉｓａｔｉｏｎ ａｎｄ ｍａｐ ｂｕｉｌｄｉｎｇ ｐｒｏｂｌｅｍ［Ｄ］． Ｓｙｄｎｅｙ：Ｕ⁃ ｎｉｖｅｒｓｉｔｙ ｏｆ Ｓｙｄｎｅｙ， １９９９： １⁃５． ［１０］熊蓉． 室内未知环境线段特征地图构建［Ｄ］． 杭州：浙 江大学， ２００９： １０⁃２３． ＸＩＯＮＧ Ｒｏｎｇ．Ｌｉｎｅ ｆｅａｔｕｒｅ ｍａｐ ｂｕｉｌｄｉｎｇ ｆｏｒ ｕｎｋｎｏｗｎ ｉｎｄｏｏｒ ｅｎｖｉｒｏｎｍｅｎｔｓ ［ Ｄ］． Ｈａｎｇｚｈｏｕ： Ｚｈｅｊｉａｎｇ Ｕｎｉｖｅｒｓｉｔｙ， ２００９： １０⁃２３． ［１１］ＤＩＳＳＡＮＡＹＡＫＥ Ｍ Ｗ Ｍ Ｇ， ＮＥＷＭＡＮ Ｐ， ＣＬＡＲＫ Ｓ， ｅｔ ａｌ． Ａ ｓｏｌｕｔｉｏｎ ｔｏ ｔｈｅ ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐ ｂｕｉｌｄｉｎｇ （ＳＬＡＭ） ｐｒｏｂｌｅｍ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｒｏ⁃ ｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｍａｔｉｏｎ， ２００１， １７（３）： ２２９⁃２４１． ［１２］ＣＡＳＴＥＬＬＡＮＯＳ Ｊ Ａ， ＭＯＮＴＩＥＬ Ｊ Ｍ Ｍ， ＮＥＩＲＡ Ｊ，ｅｔ ａｌ． Ｔｈｅ ＳＰｍａｐ： Ａ ｐｒｏｂａｂｉｌｉｓｔｉｃ ｆｒａｍｅｗｏｒｋ ｆｏｒ ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏ⁃ ｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐ ｂｕｉｌｄｉｎｇ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｒｏ⁃ ｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｍａｔｉｏｎ， １９９９， １５（５）： ９４８⁃９５２． ［１３］ＷＩＬＬＩＡＭＳ Ｓ， ＤＩＳＳＡＮＡＹＡＫＥ Ｇ， ＤＵＲＲＡＮＴ⁃ＷＨＹＴＥ Ｈ Ｆ． Ｔｏｗａｒｄｓ ｔｅｒｒａｉｎ⁃ａｉｄｅｄ ｎａｖｉｇａｔｉｏｎ ｆｏｒ ｕｎｄｅｒｗａｔｅｒ ｒｏｂｏｔｉｃｓ ［Ｊ］． Ａｄｖａｎｃｅｄ Ｒｏｂｏｔｉｃｓ， ２００１， １５（５）： ５３３⁃５４９． ［１４］ ＴＨＲＵＮ Ｓ． Ｐｒｏｂａｂｉｌｉｓｔｉｃ ａｌｇｏｒｉｔｈｍｓ ｉｎ ｒｏｂｏｔｉｃｓ ［ Ｊ］． ＡＩ Ｍａｇａｚｉｎｅ， ２０００， ２１（４）： ９３⁃１０９． ［１５］ ＨＡＨＮＥＬ Ｄ， ＢＵＲＧＡＲＤ Ｗ， ＦＯＸ Ｄ，ｅｔ ａｌ． Ａｎ ｅｆｆｉｃｉｅｎｔ ＦａｓｔＳＬＡＭ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｇｅｎｅｒａｔｉｎｇ ｍａｐｓ ｏｆ ｌａｒｇｅ⁃ｓｃａｌｅ ｃｙ⁃ ｃｌｉｃ ｅｎｖｉｒｏｎｍｅｎｔｓ ｆｒｏｍ ｒａｗ ｌａｓｅｒ ｒａｎｇｅ ｍｅａｓｕｒｅｍｅｎｔｓ ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ２００３ ＩＥＥＥ／ ＲＳＪ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎ⁃ ｆｅｒｅｎｃｅ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｒｏｂｏｔｓ ａｎｄ Ｓｙｓｔｅｍｓ． Ｌａｓ Ｖｅｇａｓ， ＮＶ， ２００３： ２０６⁃２１１． ［１６］李一波， 张庆涛． 室内未知环境遍历路径规划算法综述 ［Ｊ］． 计算机科学， ２０１２， ３９（１１Ａ）： ３３４⁃３３８． ＬＩ Ｙｉｂｏ，ＺＨＡＮＧ Ｑｉｎｇｔａｏ．Ｒｅｖｉｅｗ ｏｆ ｃｏｖｅｒａｇｅ ｐａｔｈ ｐｌａｎｎｉｎｇ ａｒｉｔｈｍｅｔｉｃ ｉｎ ｕｎｋｎｏｗｎ ｉｎｄｏｏｒ ｅｎｖｉｒｏｎｍｅｎｔ ［ Ｊ］． Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅ，２０１２， ３９（１１Ａ）： ３３４⁃３３８． ［１７］ ＵＬＲＩＣＨ Ｉ， ＭＯＮＤＡＤＡ Ｆ， ＮＩＣＯＵＤ Ｊ Ｄ． Ａｕｔｏｎｏｍｏｕｓ ｖａｃｕｕｍ ｃｌｅａｎｅｒ［ Ｊ］． Ｒｏｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｎｏｍｏｕｓ Ｓｙｓｔｅｍｓ， １９９７， １９（３）： ２３３⁃２４５． ［１８］ＯＨ Ｊ Ｓ， ＰＡＲＫ Ｊ Ｂ， ＣＨＯＩ Ｙ Ｈ． Ｃｏｍｐｌｅｔｅ ｃｏｖｅｒａｇｅ ｎａｖｉ⁃ ｇａｔｉｏｎ ｏｆ ｃｌｅａｎ ｒｏｂｏｔ ｂａｓｅｄ ｏｎ ｔｒｉａｎｇｕｌａｒ ｃｅｌｌ ｍａｐ ［ Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｄｕｓｔｒｉａｌ Ｅｌｅｃｔｒｏｎｉｃｓ， ２００４， ５１ （３）： ７１８⁃７２６． ［１９］ＪＥＢＡＲＩ Ｉ， ＢＡＺＥＩＬＬＥ Ｓ， ＦＩＬＬＩＡＴ Ｄ． Ｉｎｆｏｒｍａｔｉｃｓ ｉｎ ｃｏｎ⁃ ｔｒｏｌ， ａｕｔｏｍａｔｉｏｎ ａｎｄ ｒｏｂｏｔｉｃｓ ［ Ｍ ］． Ｂｅｒｌｉｎ： Ｓｐｒｉｎｇｅｒ， ２０１２：２２４⁃２３７． 作者简介： 马健，１９９０ 年生，男，硕士研究生， 主要研究方向为演化计算、强化学习。 俞扬，１９８２ 年生，男，助理研究员， 博士，主要研究方向为人工智能、机器 学习、演化计算、强化学习，发表学术论 文 ２０ 余篇。 ·３１８· 智 能 系 统 学 报 第 ９ 卷