
第9卷第1期 智能系统学报 Vol.9 No.1 2014年2月 CAAI Transactions on Intelligent Systems Feb.2014 D0:10.3969/j.issn.1673-4785.201309020 网络出版地址:http:/www.cmki.net/kcms/doi/10.3969/j.issn.1673-4785.201309020.html 共演博弈下的网络合作 仇建平 (太原科技大学计算机科学与技术学院,山西太原030024) 摘要:针对社会网络上个体之间的竞争与合作,设计了社会网络模型。通过引入博弈理论,仿真社会网络个体间 复杂的交互关系,即合作者或背叛者依据收益矩阵和邻居节点进行博弈。仿真结果显示当影响度过低或过高时,合 作不易形成,影响度适中时合作水平最高:当收益固定时,合作变为扩散,形成更高的威望。最后,通过MovieLens数 据集验证了群聚效应的存在,分析了舆论领袖对于网络群体的巨大影响力。 关键词:社会网络:共演博弈:合作:群聚效应:舆论领袖 中图分类号:TP393.4文献标志码:A文章编号:1673-4785(2014)01-0088-04 中文引用格式:仇建平.共演博弈下的网络合作[J].智能系统学报,2014,9(1):88-91. 英文引用格式:QIU Jianping.Network cooperation of co-evolutionary games[J].CAAI Transactions on Intelligent Systems,2014, 9(1):88-91. Network cooperation of co-evolutionary games QIU Jianping (Institute of Computer Science and technology,Taiyuan University of Science and Technology,Taiyuan 030024,China) Abstract:In accordance with competition and cooperation among individuals in social networks,a social network model has been designed.Game theory is introduced to simulate the complicated interaction relations among individ- uals in social networks.Cooperators or defectors interact with their neighbors following the payoff matrix.It can be seen that the cooperative behavior is easy to extinct for too low or too high values of degrees of influence,and the maximum cooperation level is achieved for medium values of degrees of influence.When the reward is fixed,the co- operative behavior can gradually diffuse and build higher reputations.Finally,we verified the existence of the clus- ter effect based on the MovieLens dataset and analyzed important influences of opinion leaders in netizen groups. Keywords:social network;co-evolutionary game;cooperation;cluster effect;opinion leader 随着基于社会网络的媒体及其应用的迅速发 作的影响:2)合作与演化的共演:3)网络拓扑与群 展,人们越来越多地参与到社会网络上丰富的活动 聚效应。其中,P.S.Dodds和D.J.Watts!研究了 中,社会网络应用在人们的日常生活中发挥了越来 社会网络传播中的累积效应,E.Agliari等[探讨了 越重要的作用四。社会网络是指社会个体成员之 社会网络传播中的演化问题。本文则把社会网络中 间因为互动而形成的相对稳定的复杂网络,其关注 的合作共演博弈作为研究的重点,主要集中于网络 的是个体之间的互动和联系,这种复杂的社会结构 个体间的动态交互对于合作的影响以及社会网络中 对个体行为的价值偏向以及大众舆论的形成起着至 的群聚效应。 关重要的作用。社会网络分析有着重要的现实意 义,在市场营销、广告发布、舆情预警以及社会安定 1社会网络模型 等方面有十分重要的应用2]。社会网络分析作为 一般将社会网络抽象为一张有向加权网络 一种应用性很强的研究方法,引起了国内外学者的 G(t)={N(t),L(t)f},其中N(t)为社会网络中的 关注,主要集中于以下三方面:1)网络拓扑对于合 节点(称为个体),其状态集合用S来表示;L(t)为 社会网络中的链路,链路有一个权重(影响度)h, 收稿日期:2013-09-07.网络出版日期:2014-02-20 定义了链路对节点态度和立场的影响;∫是一个 基金项目:山西省回国留学人员科研基金资助项目(2013-097). 通信作者:仇建平.E-mail:920868329@qq.com. N×N的映射,即G的拓扑图。网络的状态方程如
第 9 卷第 1 期 智 能 系 统 学 报 Vol.9 №.1 2014 年 2 月 CAAI Transactions on Intelligent Systems Feb. 2014 DOI:10.3969 / j.issn.1673⁃4785.201309020 网络出版地址:http: / / www.cnki.net / kcms/ doi / 10.3969 / j.issn.1673⁃4785.201309020.html 共演博弈下的网络合作 仇建平 (太原科技大学 计算机科学与技术学院,山西 太原 030024) 摘 要:针对社会网络上个体之间的竞争与合作,设计了社会网络模型。 通过引入博弈理论,仿真社会网络个体间 复杂的交互关系,即合作者或背叛者依据收益矩阵和邻居节点进行博弈。 仿真结果显示当影响度过低或过高时,合 作不易形成,影响度适中时合作水平最高;当收益固定时,合作变为扩散,形成更高的威望。 最后,通过 MovieLens 数 据集验证了群聚效应的存在,分析了舆论领袖对于网络群体的巨大影响力。 关键词:社会网络;共演博弈;合作;群聚效应;舆论领袖 中图分类号:TP393.4 文献标志码:A 文章编号:1673⁃4785(2014)01⁃0088⁃04 中文引用格式:仇建平.共演博弈下的网络合作[J]. 智能系统学报, 2014, 9(1): 88⁃91. 英文引用格式:QIU Jianping. Network cooperation of co⁃evolutionary games[J]. CAAI Transactions on Intelligent Systems, 2014, 9(1): 88⁃91. Network cooperation of co⁃evolutionary games QIU Jianping (Institute of Computer Science and technology, Taiyuan University of Science and Technology, Taiyuan 030024, China) Abstract:In accordance with competition and cooperation among individuals in social networks, a social network model has been designed. Game theory is introduced to simulate the complicated interaction relations among individ⁃ uals in social networks. Cooperators or defectors interact with their neighbors following the payoff matrix. It can be seen that the cooperative behavior is easy to extinct for too low or too high values of degrees of influence, and the maximum cooperation level is achieved for medium values of degrees of influence. When the reward is fixed, the co⁃ operative behavior can gradually diffuse and build higher reputations. Finally, we verified the existence of the clus⁃ ter effect based on the MovieLens dataset and analyzed important influences of opinion leaders in netizen groups. Keywords:social network; co⁃evolutionary game; cooperation; cluster effect; opinion leader 收稿日期:2013⁃09⁃07. 网络出版日期:2014⁃02⁃20. 基金项目:山西省回国留学人员科研基金资助项目(2013⁃097). 通信作者:仇建平. E⁃mail: 920868329@ qq.com. 随着基于社会网络的媒体及其应用的迅速发 展,人们越来越多地参与到社会网络上丰富的活动 中,社会网络应用在人们的日常生活中发挥了越来 越重要的作用[1] 。 社会网络是指社会个体成员之 间因为互动而形成的相对稳定的复杂网络,其关注 的是个体之间的互动和联系, 这种复杂的社会结构 对个体行为的价值偏向以及大众舆论的形成起着至 关重要的作用。 社会网络分析有着重要的现实意 义,在市场营销、广告发布、舆情预警以及社会安定 等方面有十分重要的应用[2⁃3] 。 社会网络分析作为 一种应用性很强的研究方法, 引起了国内外学者的 关注,主要集中于以下三方面:1) 网络拓扑对于合 作的影响;2)合作与演化的共演;3)网络拓扑与群 聚效应。 其中,P. S. Dodds 和 D. J. Watts [4] 研究了 社会网络传播中的累积效应,E. Agliari 等[5] 探讨了 社会网络传播中的演化问题。 本文则把社会网络中 的合作共演博弈作为研究的重点,主要集中于网络 个体间的动态交互对于合作的影响以及社会网络中 的群聚效应。 1 社会网络模型 一般将社会网络抽象为一张有向加权网络 G(t) = {N(t),L(t),f} ,其中 N(t) 为社会网络中的 节点(称为个体),其状态集合用 S 来表示; L(t) 为 社会网络中的链路,链路有一个权重(影响度) h, 定义了链路对节点态度和立场的影响; f 是一个 N ×N 的映射,即 G 的拓扑图。 网络的状态方程如

第1期 仇建平:共演博弈下的网络合作 ·89. 式(1)所示。 表1收益矩阵 s,(t+1)=s(t)+∑[s(t)-s(t)]m= Table 1 Payoff matrix 收益 c D s,()+∑△s,() (1) C R S 式中:△s,()=∑[n'(i,)(s,-s:)]代表个体i在 D T P 在每一个时间单位内,社会网络中的个体会以 社会网络中每次互动后其态度改变的量。如果 一定的概率改变其状态。比如,当网络个体x随机 L(t)的谱隙小于0,则△s(t)=Ls,(t)(L为L(t) 选择邻居个体y,并受其影响改变状态的概率[)如 转置矩阵的拉普拉斯算子),网络便会同步,即相邻 个体之间的态度没有区别,达成认同61,如式(2)所 式(3)所示。 1 示,否则陷入僵局。 (3) s(t+1)=s:(t)+Ls:(t)= W(x→)=1+exp[-(P.-U,)/K 式中:个体的平均收益P,表征了个体具有的能量 [I+L]s,(t)=[1+L]s,(0) (2) 而个体所有邻居的平均收益U.则代表了个体所处 在社会网络中,个体状态的变化由个体本身的 的势阱的能量:K表示选择邻居的随机性,K=0代 状态及与相邻个体之间的状态差异来决定,即个体 表下一个邻居已确定,K=∞代表下一邻居为随机。 能量和势阱的能量(个体受到的平均压力)。 在仿真博弈中,采用经济人假设,即网络个体的行为 社会网络是网络中的个体基于局部信息行动的 动机根源于经济诱因,网络个体都要争取最大的经 智能性、自适应性的主体网络,网络内的个体的行为 济利益,因此将个体之间的影响度h定义为平均收益。 遵循一定的规则,根据“环境”和接收信息来调整自 随着仿真博弈的进行,网络个体状态会不断变 身的状态和行为。通过网络内个体之间的相互竞 化。设n(t)为在仿真时间单位t内网络个体x的 争、协作等局部相互作用,在整体上显现出更高层 邻居中改变状态的邻居个数。.(t)越大表明x越 次、更加复杂、更加协调的有序性。 多的邻居改变状态,这暗示着个体x在邻居中有着 2仿真博弈 更大的威望,处于群体领袖地位,网络个体x的威望 可定义为式(4): 在仿真系统中建立一个网络人群,其人口规模 R(t+1)=R(t)+h×n(t) (4)】 为M,由2种个体行为状态组成),即M=C+D, 设初始状态R(0)=0,当影响度h为0时,表示 其中C为合作者(用(0,1]的正数表示),D为背叛 个体无法影响他人,从而无法改变邻居状态,当h不 者(用[-1,0)的负数表示),每个个体都只与其邻 为0时,表示个体有能力影响他人,随着h的增加, 居进行交互。 个人威望也快速增长。同时,n(t)的增长也促进 在时间维上,将仿真的全部过程分成若干个仿 了威望的增长。 真时间单位。在每一个时间单位内,每个网络个体 最多只能与一个邻居个体交互一次,并且最多只能 3仿真系统及结果分析 变换一次个体行为状态,状态的变化取决于收益的 3.1仿真系统 博弈,其收益矩阵如表1所示。合作者C遇到背叛 在仿真系统中,根据文献[8]生成无标度网络, 者D,合作者收益为S,背叛者收益为T;2个合作 起始网络为3个节点的完全网络,每次有3条边与 者相遇,收益均为R:2个背叛者相遇,收益均为P, 新节点相连,每个仿真时间单位以概率P(k:)= 收益值的大小为T>R>S>P。当2个个体陷入 僵局时所需付出的代价为c,带来的收益为b。如 k/∑添加一个节点来增长网络,生成的无标度 果2人都为合作者,则他们的收益为R=b-c/2;如 网络服从幂律分布,从而构建仿真社会网络。 果只有一人付出代价,虽然2个个体都可以获得好 在仿真系统中将社会网络个体抽象为具有自主 处,但背叛者未付出代价,背叛者收益为T=b,而合 学习、自主适应和自主组织的智能代理Agent,利用 作者的收益为S=b-c;如果2人都选择不合作,即 Agent可以模拟个体之间复杂的相互作用,容易实 2人都为背叛者,2人都被无法改变对方状态,则他 现个体的差异化及个体的决策行为。网络模型的系 们的收益都为P=0。不失一般性,假定b-c/2为 统框架如图1所示。系统初始化模块包括两部分, 1,则损益比为1=分20-。0<r<》,7=1+ 分别用来配置初始参数和Agent的初始设置。其中, K为0.1,仿真时间单位为0.5s,R=100,合作者密 R=1,S=1-r,P=0。 度f=合作者人数/总人数N,最初只有一个背叛者
式(1)所示。 si(t + 1) = si(t) + ∑ j [sj(t) - si(t)]η T = si(t) + ∑ j Δ si(t) (1) 式中: Δ si(t) =∑ j [η T (i,j)(sj - si)] 代表个体 i 在 社会网络中每次互动后其态度改变的量。 如果 L(t) 的谱隙小于 0,则 Δ si(t) = Lsi(t) ( L 为 L(t) 转置矩阵的拉普拉斯算子),网络便会同步,即相邻 个体之间的态度没有区别,达成认同[ 6 ] ,如式(2)所 示,否则陷入僵局。 si(t + 1) = si(t) + L si(t) = [I + L] si(t) = [I + L ] si(0) (2) 在社会网络中,个体状态的变化由个体本身的 状态及与相邻个体之间的状态差异来决定,即个体 能量和势阱的能量(个体受到的平均压力)。 社会网络是网络中的个体基于局部信息行动的 智能性、自适应性的主体网络,网络内的个体的行为 遵循一定的规则,根据“环境”和接收信息来调整自 身的状态和行为。 通过网络内个体之间的相互竞 争、协作等局部相互作用,在整体上显现出更高层 次、更加复杂、更加协调的有序性。 2 仿真博弈 在仿真系统中建立一个网络人群,其人口规模 为 M ,由 2 种个体行为状态组成[7] ,即 M = C + D , 其中 C 为合作者(用 (0,1] 的正数表示), D 为背叛 者(用 [ - 1,0) 的负数表示),每个个体都只与其邻 居进行交互。 在时间维上,将仿真的全部过程分成若干个仿 真时间单位。 在每一个时间单位内,每个网络个体 最多只能与一个邻居个体交互一次,并且最多只能 变换一次个体行为状态,状态的变化取决于收益的 博弈,其收益矩阵如表 1 所示。 合作者 C 遇到背叛 者 D ,合作者收益为 S ,背叛者收益为 T ;2 个合作 者相遇,收益均为 R ;2 个背叛者相遇,收益均为 P , 收益值的大小为 T > R > S > P。 当 2 个个体陷入 僵局时所需付出的代价为 c ,带来的收益为 b 。 如 果 2 人都为合作者,则他们的收益为 R = b - c/ 2; 如 果只有一人付出代价,虽然 2 个个体都可以获得好 处,但背叛者未付出代价,背叛者收益为 T = b ,而合 作者的收益为 S = b - c ;如果 2 人都选择不合作,即 2 人都为背叛者,2 人都被无法改变对方状态,则他 们的收益都为 P = 0。 不失一般性,假定 b -c/ 2 为 1,则损益比为 r = c 2 = c 2b - c (0 < r < 1),T =1 + r, R = 1,S = 1 - r,P = 0。 表 1 收益矩阵 Table 1 Payoff matrix 收益 C D C D R T S P 在每一个时间单位内,社会网络中的个体会以 一定的概率改变其状态。 比如,当网络个体 x 随机 选择邻居个体 y ,并受其影响改变状态的概率[8] 如 式(3)所示。 W(x → y) = 1 1 + exp[ - (Px - Ux) / K] (3) 式中:个体的平均收益 Px 表征了个体具有的能量, 而个体所有邻居的平均收益 Ux 则代表了个体所处 的势阱的能量; K 表示选择邻居的随机性, K = 0 代 表下一个邻居已确定, K = ¥代表下一邻居为随机。 在仿真博弈中,采用经济人假设,即网络个体的行为 动机根源于经济诱因,网络个体都要争取最大的经 济利益,因此将个体之间的影响度 h 定义为平均收益。 随着仿真博弈的进行,网络个体状态会不断变 化。 设 nx(t) 为在仿真时间单位 t 内网络个体 x 的 邻居中改变状态的邻居个数。 nx(t) 越大表明 x 越 多的邻居改变状态,这暗示着个体 x 在邻居中有着 更大的威望,处于群体领袖地位,网络个体 x 的威望 可定义为式(4): Rx(t + 1) = Rx(t) + h × nx(t) (4) 设初始状态 R(0) = 0,当影响度 h 为 0 时,表示 个体无法影响他人,从而无法改变邻居状态,当 h 不 为 0 时,表示个体有能力影响他人,随着 h 的增加, 个人威望也快速增长。 同时, nx(t) 的增长也促进 了威望的增长。 3 仿真系统及结果分析 3.1 仿真系统 在仿真系统中,根据文献[8]生成无标度网络, 起始网络为 3 个节点的完全网络,每次有 3 条边与 新节点相连, 每个仿真时间单位以概率 P(ki) = ki /∑ j kj 添加一个节点来增长网络,生成的无标度 网络服从幂律分布,从而构建仿真社会网络。 在仿真系统中将社会网络个体抽象为具有自主 学习、自主适应和自主组织的智能代理 Agent ,利用 Agent 可以模拟个体之间复杂的相互作用,容易实 现个体的差异化及个体的决策行为。 网络模型的系 统框架如图 1 所示。 系统初始化模块包括两部分, 分别用来配置初始参数和 Agent 的初始设置。 其中, K 为 0.1,仿真时间单位为 0.5 s, Rmax = 100,合作者密 度 f c = 合作者人数/ 总人数 Nt ,最初只有一个背叛者 第 1 期 仇建平:共演博弈下的网络合作 ·89·
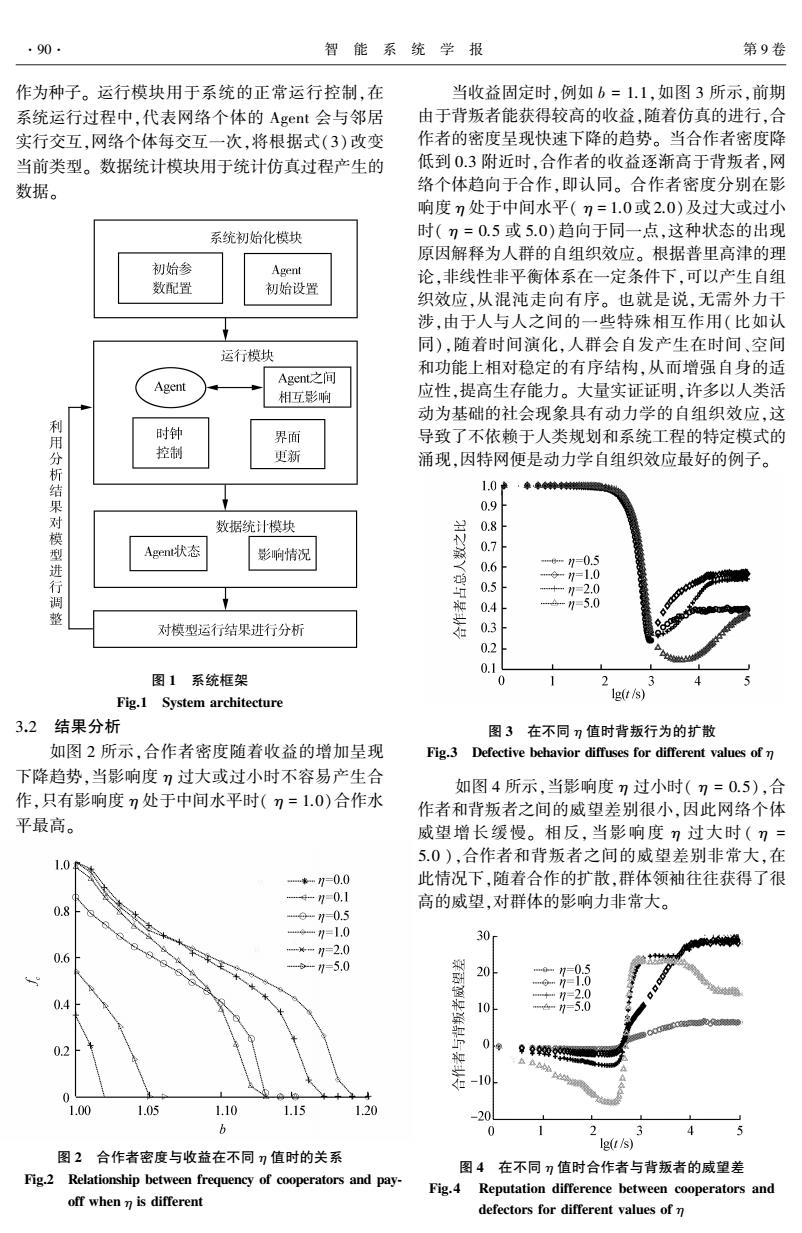
90 智能系统学报 第9卷 作为种子。运行模块用于系统的正常运行控制,在 当收益固定时,例如b=1.1,如图3所示,前期 系统运行过程中,代表网络个体的Agent会与邻居 由于背叛者能获得较高的收益,随着仿真的进行,合 实行交互,网络个体每交互一次,将根据式(3)改变 作者的密度呈现快速下降的趋势。当合作者密度降 当前类型。数据统计模块用于统计仿真过程产生的 低到03附近时,合作者的收益逐渐高于背叛者,网 数据。 络个体趋向于合作,即认同。合作者密度分别在影 响度7处于中间水平(7=1.0或2.0)及过大或过小 系统初始化模块 时(7=0.5或5.0)趋向于同一点,这种状态的出现 原因解释为人群的自组织效应。根据普里高津的理 初始参 Agent 论,非线性非平衡体系在一定条件下,可以产生自组 数配置 初始设置 织效应,从混沌走向有序。也就是说,无需外力干 涉,由于人与人之间的一些特殊相互作用(比如认 同),随着时间演化,人群会自发产生在时间、空间 运行模块 和功能上相对稳定的有序结构,从而增强自身的适 Agent之间 Agent 相互影响 应性,提高生存能力。大量实证证明,许多以人类活 动为基础的社会现象具有动力学的自组织效应,这 时钟 利用分析结果 界面 导致了不依赖于人类规划和系统工程的特定模式的 控制 更新 涌现,因特网便是动力学自组织效应最好的例子。 1.0 0.9 数据统计模块 模型进行调整 Agent状态 影响情况 -m1=0.5 mg-1=1.0 -=2.0 42 1=5.0 对模型运行结果进行分析 0.2 0.1 图1系统框架 2 Fig.1 System architecture lg(t/s) 3.2结果分析 图3在不同)值时背叛行为的扩散 如图2所示,合作者密度随着收益的增加呈现 Fig.3 Defective behavior diffuses for different values of 下降趋势,当影响度)过大或过小时不容易产生合 如图4所示,当影响度7过小时(7=0.5),合 作,只有影响度)处于中间水平时()=1.0)合作水 作者和背叛者之间的威望差别很小,因此网络个体 平最高。 威望增长缓慢。相反,当影响度)过大时(η三 5.0),合作者和背叛者之间的威望差别非常大,在 1.0 =…*1=0.0 此情况下,随着合作的扩散,群体领袖往往获得了很 4-1-0.1 0.8 高的威望,对群体的影响力非常大。 010.5 ◆=1.0 30 …4-1=2.0 0.6 o-1=5.0 0.4 0 +1=2.0 4-15.0 0.2 0 90细 -10L 1.00 1.05 1.10 1.15 1.20 -20L b 2 Ig(t/s) 图2合作者密度与收益在不同刀值时的关系 图4在不同η值时合作者与背叛者的威望差 Fig.2 Relationship between frequency of cooperators and pay- Fig.4 Reputation difference between cooperators and off when m is different defectors for different values of
作为种子。 运行模块用于系统的正常运行控制,在 系统运行过程中,代表网络个体的 Agent 会与邻居 实行交互,网络个体每交互一次,将根据式(3)改变 当前类型。 数据统计模块用于统计仿真过程产生的 数据。 图 1 系统框架 Fig.1 System architecture 3.2 结果分析 如图 2 所示,合作者密度随着收益的增加呈现 下降趋势,当影响度 η 过大或过小时不容易产生合 作,只有影响度 η 处于中间水平时( η = 1.0)合作水 平最高。 图 2 合作者密度与收益在不同 η 值时的关系 Fig.2 Relationship between frequency of cooperators and pay⁃ off when η is different 当收益固定时,例如 b = 1.1,如图 3 所示,前期 由于背叛者能获得较高的收益,随着仿真的进行,合 作者的密度呈现快速下降的趋势。 当合作者密度降 低到 0.3 附近时,合作者的收益逐渐高于背叛者,网 络个体趋向于合作,即认同。 合作者密度分别在影 响度 η 处于中间水平( η = 1.0 或2.0)及过大或过小 时( η = 0.5 或 5.0)趋向于同一点,这种状态的出现 原因解释为人群的自组织效应。 根据普里高津的理 论,非线性非平衡体系在一定条件下,可以产生自组 织效应,从混沌走向有序。 也就是说,无需外力干 涉,由于人与人之间的一些特殊相互作用(比如认 同),随着时间演化,人群会自发产生在时间、空间 和功能上相对稳定的有序结构,从而增强自身的适 应性,提高生存能力。 大量实证证明,许多以人类活 动为基础的社会现象具有动力学的自组织效应,这 导致了不依赖于人类规划和系统工程的特定模式的 涌现,因特网便是动力学自组织效应最好的例子。 图 3 在不同 η 值时背叛行为的扩散 Fig.3 Defective behavior diffuses for different values of η 如图 4 所示,当影响度 η 过小时( η = 0.5),合 作者和背叛者之间的威望差别很小,因此网络个体 威望增长缓慢。 相反,当影响度 η 过大时 ( η = 5.0 ),合作者和背叛者之间的威望差别非常大,在 此情况下,随着合作的扩散,群体领袖往往获得了很 高的威望,对群体的影响力非常大。 图 4 在不同 η 值时合作者与背叛者的威望差 Fig.4 Reputation difference between cooperators and defectors for different values of η ·90· 智 能 系 统 学 报 第 9 卷

第1期 仇建平:共演博弈下的网络合作 ·91- 随着计算机技术的广泛使用和社会网络的成 统,网络中的每一个人都不自觉地被所处的环境所 熟普及,人们在享受着前所未有的便捷的同时,在利 影响。本文研究了社会网络上的合作博弈行为。首 益格局固定的情况下,处于某一利益共同体的个体, 先通过无标度上个体博弈结果,得到个体影响度对 个性就会自觉地消失而群体的共性便随之显现出 网络合作水平的作用:其次探索了合作收益固定时, 来,即形成所谓的“群体效应”,如图5、6所示。 影响网络个体威望的因素:最后阐述了群聚效应的 存在及社交网络中舆论领袖的影响。研究结果将对 探讨社交网络中的某些现象提供帮助。 参考文献: 20 40 60 80 100 [1]PAN Wei,AHARONY N,PENTLAND A.Composite social 电影序列 network for predicting mobile apps installation[C]//The 图5五分制评分序列 25th AAAI Conference on Artificial Intelligence.San Fran- Fig.5 Five grade Grading sequence cisco,USA:AAAI Press,2011:821-827. [2]ZHANG Chengjun,ZENG An.Behavior patterns of online users and the effect on information filtering[J].Physical A: 20 40 60 80 100 Statistical Mechanics and its Applications,2011,391(12): 电影序列 1822-1830. [3]GUO S,WANG Mengqiu,LESKOVEC J.The role of social 图6正负分评分序列 networks in online shopping:information passing,price of Fig.6 Positive and negative grading sequence trust,and consumer choice[C]//The 12th ACM Conference 利用MovieLens站点提供的数据集(htp:// on Electronic Commerce.New York,USA:ACM Press, 2011:157-166. wvw.grouplens..org)来验证群聚效应的存在。Mov- ieLens数据集由美国明尼苏达大学的GroupLens研 [4]DODDS P S,WATTS D J.Universal behavior in a general- ized model of contagion J.Physical Review Letter,2004, 究项目组收集,是一个基于网络的推荐系统,包含了 简要的用户统计信息。数据集包括71567个用户 92(21):1-4. [5]AGLIARI E,BURIONI R,CASSI D,et al.Efficiency of 对10681部电影的10000054个评分。 通过观察评分,发现在高分对象后面的打分 information spreading in a population of diffusing agents[. Physical Review E.2006,73(1):1-16. 普遍高,而在低分对象后面的打分普遍也低。进一 [6]GABBAY M.The effects of nonlinear interactions and net- 步地,采用去除均值偏移的办法将打分分成2类:相 work structure in small group opinion dynamics[J].Physi- 比而言偏高的打分和相比而言偏低的打分。图5为 calA,2007,378(1):118-126. 某一用户按五分制对电影的打分,图6中白色表示 [7]AXELROD R.The evolution of cooperation[M].New York: 为正分,黑色为负分。从图5中可以看出,这是一个 American Association for the Advancement of Science, 典型的用户打分偏高和偏低出现的序列,这种统计 1981:1390-1396. 具有显著的群聚效应,即偏高分和偏低分倾向于集 [8]SZABO G.TOKE C.Evolutionary prisoner's dilemma game 中一起出现。 on a square lattice[J].Physical Review E,1998,58(1): 在社会网络中,网民的个人责任感极容易消失, 69-73. 从而变得非常烦躁、多变和冲动]。这时网民的理 [9]王根生.网络舆情群体极化动力模型与仿真分析[J].情 智不容易受控制,所谓的真相变得无足轻重,取而代 报杂志,2012,31(3):20-24. 之的是具有浓重感情色彩的主观价值判断。网民归 WANG Gensheng.Dynamic model and simulation analysis of 属群体的舆论领袖往往影响着网民群体的思维方 group polarization of online public opinion[J].Journal of 式,左右着大众的观点和看法。原因解释如下。 Intelligence,2012,31(3):20-24. 1)群体的推理判断能力往往低于孤立的个体, [10]MOSCOVICI S.The age of the crowd:a historical treatise 而群体态度的选择也很大程度上取决于群体领袖, on mass psychology[M].Cambridge:Cambridge Universi- 群体对领袖暗示盲从的心理特征,让领袖暗示的价 ty Press,1985:439.450 值取向变得尤为重要。当群体领袖所传播的信息客观 作者简介: 公正时,群体的态度选择往往比较理性:反之,则不然。 仇建平,男,1973年生,讲师,主要 2)舆论领袖往往充当着群体领袖的角色,且威 研究方向为复杂网络、人工智能,发表 力巨大,比如微博上的“大V”。 学术论文10余篇,参编专著1部,编写 教材1部。 4 结束语 社会网络,比如互联网,都是典型的多体关联系
随着计算机技术的广泛使用和社会网络的成 熟普及,人们在享受着前所未有的便捷的同时,在利 益格局固定的情况下,处于某一利益共同体的个体, 个性就会自觉地消失而群体的共性便随之显现出 来,即形成所谓的“群体效应”,如图 5、6 所示。 图 5 五分制评分序列 Fig.5 Five grade Grading sequence 图 6 正负分评分序列 Fig.6 Positive and negative grading sequence 利用 MovieLens 站 点 提 供 的 数 据 集 ( http: / / www.grouplens. org) 来验证群聚效应的存在。 Mov⁃ ieLens 数据集由美国明尼苏达大学的 GroupLens 研 究项目组收集,是一个基于网络的推荐系统,包含了 简要的用户统计信息。 数据集包括 71 567 个用户 对 10 681 部电影的 10 000 054 个评分。 通过观察评分[9] ,发现在高分对象后面的打分 普遍高,而在低分对象后面的打分普遍也低。 进一 步地,采用去除均值偏移的办法将打分分成 2 类:相 比而言偏高的打分和相比而言偏低的打分。 图 5 为 某一用户按五分制对电影的打分,图 6 中白色表示 为正分,黑色为负分。 从图 5 中可以看出,这是一个 典型的用户打分偏高和偏低出现的序列,这种统计 具有显著的群聚效应,即偏高分和偏低分倾向于集 中一起出现。 在社会网络中,网民的个人责任感极容易消失, 从而变得非常烦躁、多变和冲动[10] 。 这时网民的理 智不容易受控制,所谓的真相变得无足轻重,取而代 之的是具有浓重感情色彩的主观价值判断。 网民归 属群体的舆论领袖往往影响着网民群体的思维方 式,左右着大众的观点和看法。 原因解释如下。 1)群体的推理判断能力往往低于孤立的个体, 而群体态度的选择也很大程度上取决于群体领袖, 群体对领袖暗示盲从的心理特征,让领袖暗示的价 值取向变得尤为重要。 当群体领袖所传播的信息客观 公正时,群体的态度选择往往比较理性;反之,则不然。 2)舆论领袖往往充当着群体领袖的角色,且威 力巨大,比如微博上的“大 V”。 4 结束语 社会网络,比如互联网,都是典型的多体关联系 统,网络中的每一个人都不自觉地被所处的环境所 影响。 本文研究了社会网络上的合作博弈行为。 首 先通过无标度上个体博弈结果,得到个体影响度对 网络合作水平的作用;其次探索了合作收益固定时, 影响网络个体威望的因素;最后阐述了群聚效应的 存在及社交网络中舆论领袖的影响。 研究结果将对 探讨社交网络中的某些现象提供帮助。 参考文献: [1]PAN Wei, AHARONY N, PENTLAND A. Composite social network for predicting mobile apps installation[C] / / The 25th AAAI Conference on Artificial Intelligence. San Fran⁃ cisco, USA: AAAI Press, 2011: 821⁃827. [2] ZHANG Chengjun, ZENG An. Behavior patterns of online users and the effect on information filtering[J]. Physical A: Statistical Mechanics and its Applications, 2011, 391(12): 1822⁃1830. [3]GUO S, WANG Mengqiu, LESKOVEC J. The role of social networks in online shopping: information passing, price of trust, and consumer choice[C] / / The 12th ACM Conference on Electronic Commerce. New York, USA: ACM Press, 2011: 157⁃166. [4]DODDS P S, WATTS D J. Universal behavior in a general⁃ ized model of contagion[J]. Physical Review Letter, 2004, 92(21): 1⁃4. [5] AGLIARI E, BURIONI R, CASSI D, et al. Efficiency of information spreading in a population of diffusing agents[J]. Physical Review E, 2006, 73(1): 1⁃16. [6]GABBAY M. The effects of nonlinear interactions and net⁃ work structure in small group opinion dynamics[ J]. Physi⁃ cal A, 2007, 378(1): 118⁃126. [7]AXELROD R. The evolution of cooperation[M]. New York: American Association for the Advancement of Science, 1981: 1390⁃1396. [8]SZABO G, TOKE C. Evolutionary prisoners dilemma game on a square lattice[J]. Physical Review E, 1998, 58(1): 69⁃73. [9]王根生.网络舆情群体极化动力模型与仿真分析[ J].情 报杂志, 2012, 31(3): 20⁃24. WANG Gensheng. Dynamic model and simulation analysis of group polarization of online public opinion[J]. Journal of Intelligence, 2012, 31(3): 20⁃24. [10]MOSCOVICI S. The age of the crowd: a historical treatise on mass psychology[M]. Cambridge: Cambridge Universi⁃ ty Press, 1985: 439⁃450. 作者简介: 仇建平,男,1973 年生,讲师,主要 研究方向为复杂网络、人工智能,发表 学术论文 10 余篇,参编专著 1 部,编写 教材 1 部。 第 1 期 仇建平:共演博弈下的网络合作 ·91·