
第9卷第3期 智能系统学报 Vol.9 No.3 2014年6月 CAAI Transactions on Intelligent Systems Jun.2014 D0:10.3969/j.issn.1673-4785.201310014 网络出版地址:http:/www.cnki.net/kcms/doi/10.3969/j.issn.16734785.201310014.html 基于人工蜂群算法的贝叶斯网络结构学习 张平,刘三阳,朱明敏 (西安电子科技大学数学与统计学院,陕西西安710071) 摘要:从数据集中学习贝叶斯网络结构是一个NP难问题。针对此问题提出基于遗传算子的人工蜂群算法。首 先将贝叶斯网络结构映射为一种二进制编码:其次,根据贝叶斯网络的结构特点,设计了蜜源的更新策略,从而 将学习贝叶斯网络结构的过程转化为蜂群寻找最优蜜源的过程。实验结果表明,该算法应用于贝叶斯网络结构学 习中的有效性。 关键词:贝叶斯网络:NP难;人工蜂群算法;遗传算子;结构学习 中图分类号:TP181文献标志码:A文章编号:1673-4785(2014)03-0325-05 中文引用格式:张平,刘三阳,朱明敏.基于人工蜂群算法的贝叶斯网络结构学习[J].智能系统学报,2014,9(3):325329. 英文引用格式:ZHANG Ping,LIU Sanyang,ZHU Mingmin.Structure learning of Bayesian networks by use of the artificial bee colo- ny algorithm[J].CAAI Transactions on Intelligent Systems,2014,9(3):325-329. Structure learning of Bayesian networks by use of the artificial bee colony algorithm ZHANG Ping,LIU Sanyang,ZHU Mingmin (School of Mathematics and Statistics,Xidian University,Xi'an 710071,China) Abstract:The learning structure of Bayesian networks from a data set is an NP-hard problem.To deal with this problem,an artificial bee colony algorithm based on genetic operators is proposed in this paper.The structure of the Bayesian network is mapped to binary encoding,and the updated strategy of nectar is designed according to the characteristics of the Bayesian network structure.Thus the process of structure learning of the Bayesian network is transformed into the process of the bee colony finding the optimal nectar.The experimental results show that the al- gorithm is valid in the structure learning of Bayesian networks. Keywords:Bayesian networks;NP-hard;artificial bee colony;genetic operators;structure learning 贝叶斯网络(Bayesian networks,BN)Ii-2是概 Chickering在2OO2年提出贪婪算法(greedy search, 率论与图论结合的产物,已经成为处理不确定性问 GS)[。李显杰等在2008年将量子遗传算法用于 题的有效工具。近年来,如何从数据集中高效地学 贝叶斯网络结构学习,取得较好的效果,但该方法编 习贝叶斯网络结构受到了众多学者的广泛关注。一 码方式较复杂。高晓利在2011年提出了一种改进 般地,贝叶斯网络结构学习的方法可以分为两大类: 的学习贝叶斯结构的贪婪算法,该算法结合了条件 1)基于独立性测试的方法[3:2)基于评分搜索的 独立性测试方法,当节点个数增大时,条件独立性测 方法[5s。基于评分搜索的方法包括2个要素,即评 试呈指数增长,这种方法适合节点较少的网络结构。 分标准和搜索策略。由于贝叶斯网络结构学习是一 人工蜂群(artificial bee colony,ABC)算法是D 个NP难问题,因此基于评分搜索的贝叶斯网络结 Karaboga【1o2005年提出的一种群体智能优化算法。 构学习方法中的搜索算法一般采用启发式搜索算 该算法结构简单、参数较少、易于实现,受到了众多学 法。国内外的学者提出了许多基于评分搜索的方 者的关注和研究,并成功应用于函数优化.)、神经 法,例如Cooper等1992年提出了K2算法[剧。 网络训练[1]控制工程16等问题。本文将ABC算 法用于贝叶斯网络结构学习问题,具体论述了算法的 收稿日期:2013-11-04.网络出版日期:2014-06-14 基金项目:国家自然科学基金资助项目(61075055):西安电子科技大学 实现过程。最后,通过在Asia和Car网络上测试,结 基本科研业务基金资助项目(K5051270013). 果表明了本文算法的合理性和有效性。 通信作者:张平.E-mail:pzhangxdedu@163.com
第 9 卷第 3 期 智 能 系 统 学 报 Vol.9 №.3 2014 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2014 DOI:10.3969 / j.issn.1673⁃4785.201310014 网络出版地址:http: / / www.cnki.net / kcms/ doi / 10.3969 / j.issn.16734785.201310014.html 基于人工蜂群算法的贝叶斯网络结构学习 张平,刘三阳,朱明敏 (西安电子科技大学 数学与统计学院,陕西 西安 710071) 摘 要:从数据集中学习贝叶斯网络结构是一个 NP 难问题。 针对此问题提出基于遗传算子的人工蜂群算法。 首 先,将贝叶斯网络结构映射为一种二进制编码; 其次, 根据贝叶斯网络的结构特点, 设计了蜜源的更新策略, 从而 将学习贝叶斯网络结构的过程转化为蜂群寻找最优蜜源的过程。 实验结果表明, 该算法应用于贝叶斯网络结构学 习中的有效性。 关键词:贝叶斯网络;NP 难;人工蜂群算法;遗传算子;结构学习 中图分类号: TP181 文献标志码:A 文章编号:1673⁃4785(2014)03⁃0325⁃05 中文引用格式:张平,刘三阳,朱明敏. 基于人工蜂群算法的贝叶斯网络结构学习[J]. 智能系统学报, 2014, 9(3): 325⁃329. 英文引用格式:ZHANG Ping,LIU Sanyang,ZHU Mingmin. Structure learning of Bayesian networks by use of the artificial bee colo⁃ ny algorithm[J]. CAAI Transactions on Intelligent Systems, 2014, 9(3): 325⁃329. Structure learning of Bayesian networks by use of the artificial bee colony algorithm ZHANG Ping, LIU Sanyang, ZHU Mingmin (School of Mathematics and Statistics, Xidian University, Xi'an 710071, China) Abstract: The learning structure of Bayesian networks from a data set is an NP⁃hard problem. To deal with this problem, an artificial bee colony algorithm based on genetic operators is proposed in this paper. The structure of the Bayesian network is mapped to binary encoding, and the updated strategy of nectar is designed according to the characteristics of the Bayesian network structure. Thus the process of structure learning of the Bayesian network is transformed into the process of the bee colony finding the optimal nectar. The experimental results show that the al⁃ gorithm is valid in the structure learning of Bayesian networks. Keywords:Bayesian networks; NP⁃hard; artificial bee colony; genetic operators; structure learning 收稿日期:2013⁃11⁃04. 网络出版日期:2014⁃06⁃14. 基金项目:国家自然科学基金资助项目(61075055);西安电子科技大学 基本科研业务基金资助项目(K5051270013). 通信作者:张平.E⁃mail:pzhangxdedu@ 163.com. 贝叶斯网络(Bayesian networks, BN) [ 1⁃ 2] 是概 率论与图论结合的产物,已经成为处理不确定性问 题的有效工具。 近年来,如何从数据集中高效地学 习贝叶斯网络结构受到了众多学者的广泛关注。 一 般地,贝叶斯网络结构学习的方法可以分为两大类: 1)基于独立性测试的方法[3 ⁃ 4] ;2)基于评分搜索的 方法[5⁃7] 。 基于评分搜索的方法包括 2 个要素,即评 分标准和搜索策略。 由于贝叶斯网络结构学习是一 个 NP 难问题,因此基于评分搜索的贝叶斯网络结 构学习方法中的搜索算法一般采用启发式搜索算 法。 国内外的学者提出了许多基于评分搜索的方 法,例 如 Cooper 等 1992 年 提 出 了 K2 算 法[8] 。 Chickering 在 2002 年提出贪婪算法( greedy search, GS) [9] 。 李显杰等在 2008 年将量子遗传算法用于 贝叶斯网络结构学习,取得较好的效果,但该方法编 码方式较复杂。 高晓利在 2011 年提出了一种改进 的学习贝叶斯结构的贪婪算法,该算法结合了条件 独立性测试方法,当节点个数增大时,条件独立性测 试呈指数增长,这种方法适合节点较少的网络结构。 人工蜂群(artificial bee colony,ABC) 算法是 D Karaboga [10] 2005 年提出的一种群体智能优化算法. 该算法结构简单、参数较少、易于实现,受到了众多学 者的关注和研究,并成功应用于函数优化[11⁃12] 、神经 网络训练[13⁃15] 、控制工程[16]等问题。 本文将 ABC 算 法用于贝叶斯网络结构学习问题,具体论述了算法的 实现过程。 最后,通过在 Asia 和 Car 网络上测试,结 果表明了本文算法的合理性和有效性

·326· 智能系统学报 第9卷 1 贝叶斯网络 引领蜂和跟随蜂按照式(5)由蜜源X:= (x,x2,…,xD)得到新蜜源: 贝叶斯网络是一个二元组,即BN=(G,P),其 写=xg+r×(xg-x与) (5) 中G=(V,E)为一个有向无环图,表示BN的结构: 式中:k∈{1,2,…,SN}且k≠i;j∈{1,2,…,D} P表示节点的条件概率分布集合,表示节点之间的 是随机产生的整数;r∈[-1,1]是一个随机数。 依赖程度。根据条件独立性,给定BN,存在一个离 若在一定循环次数(1imit)后,蜜源质量没有提高,则 散变量集合X={V,V2,…,V}上的联合概率分布 引领蜂放弃该蜜源,转变为侦查蜂,按照式(6)随机 P(V): 产生新蜜源: P(V)=P(V,V2,...v)=IIP(VI Pa(V)) =l;rand(0,1)x (u;-) (6) 式中:l和u分别是变量x:的下界和上界。 (1) 式中:Pa(V)是V:的父节点。 3 人工蜂群算法的贝叶斯网络结构学习 假设一组随机变量x1,x2,…,x。, D= ABC算法中,学习最优贝叶斯网络结构的过程 (D1,D2,…,D)是关于这组变量独立分布的数据 就是蜂群寻找高收益蜜源的过程。引领蜂能够保持 集。贝叶斯网络的结构学习就是尽可能结合先验知 优良蜜源,有精英特性:跟随蜂能够增加较优蜜源对 识,找到和样本数据D拟合最好的网络结构。测试 应的蜜蜂数量,加速算法的收敛:侦查蜂任意搜索新 网络结构与样本集匹配程度的函数称为评分函数。 蜜源,增加了蜜源的多样性,有利于算法跳出局部最 本文采用基于贝叶斯统计思想的贝叶斯评分函数: 优。2个过程的对应关系如表1所示。 9 P(D1S)=Π r( T(a话+Nt) 表12个过程的对应关系 I(ag+Ni) I(a) Table 1 The corresponding relation of the two processes (2) 蜂群寻找蜜源过程 贝叶斯网络结构学习过程 式中:N#是D中满足x:=k、Pa(x)=j的样本个数, 蜜源位置 所有贝叶斯网络结构 ∑N,= 蜜源的收益 贝叶斯网络的得分 Ni= k=1 三心:,取一个等价样本,其数量 高收益蜜源 最优贝叶斯网络结构 为N,t= 3.1贝叶斯网络结构的编码 9T: 文中采用文献[17]中的矩阵编码方式,一个包 2 人工蜂群算法原理 含n个节点的贝叶斯网络可以表示为n×n的矩阵 A={ar},其中a定义如下: ABC算法中,蜜源的位置表示问题的候选解, 1j是i的父节点 花蜜数量反映解的质量。最优蜜源的确定依靠人工 a,={0,否则 蜂群的迭代搜索。人工蜂群包括3类:引领蜂、跟随 本文算法中表示贝叶斯网络结构的个体为 蜂和侦查蜂。引领蜂标记较优蜜源,并将信息传递 给跟随蜂,跟随蜂根据蜜源的花蜜数量选择蜜源进 a11a21…an1a12a22…a2a1na2n…0m 3.2 基于遗传算子的蜜源更新策略 行更新,侦查蜂随机搜索新蜜源。 人工蜂群算法一般用于解决连续优化问题,而 设在D维空间中,种群规模为2×SN(引领蜂个 贝叶斯网络结构为二进制编码,因此不能直接应用 数=跟随蜂个数=SN),蜜源与引领蜂一一对应,即 ABC算法中式(5)产生新蜜源。考虑式(5),实际上 蜜源数目为SN,第i个蜜源的位置记为X,= 是两个蜜源之间信息的分享以及个体蜜源自身特性 (x1,x2,…,xD)。算法的迭代过程中,跟随蜂根据 的继承,这类似于遗传算法中的交叉和变异算子,所 引领蜂分享的信息,以轮盘赌的方式根据式(3)选 以采用交叉和变异两种算子对蜜源进行更新。 择一个蜜源: 在交叉算子中,本文采用rand和best两种交叉 fit P.= (3) 策略。其中rand交叉策略是指随机选择一个蜜源 SN 与待更新蜜源进行两点交叉,能够增强种群之间的 i=1 信息共享:best交叉策略是指利用当前最优蜜源与 式中:ft:是花蜜数量(适应度),按照式(4)计算: 待更新蜜源进行两点交叉,有利于最优蜜源特性的 1 继承。文中通过参数p来决定采取哪种交叉策略, fit=+f f≥0 (4) p的取值将在实验部分讨论。 1 abs(f)f< 在变异算子中,有加边、删边和反转边3种变异 式中f是第i个解的目标函数值。 操作。本文通过随机均匀产生1、2、3的任意一个整
1 贝叶斯网络 贝叶斯网络是一个二元组,即 BN = (G,P) ,其 中 G = (V,E) 为一个有向无环图,表示 BN 的结构; P 表示节点的条件概率分布集合,表示节点之间的 依赖程度。 根据条件独立性,给定 BN,存在一个离 散变量集合 X = V1 ,V2 ,…,Vn { } 上的联合概率分布 P(V) : P(V) = P V1 ,V2 ,…,Vn ( ) = Π n i = 1 P Vi | Pa Vi ( ( ) ) (1) 式中: Pa(Vi) 是 Vi 的父节点。 假 设 一 组 随 机 变 量 x1 ,x2 ,…,xn , D = D1 ,D2 ,…,Dn ( ) 是关于这组变量独立分布的数据 集。 贝叶斯网络的结构学习就是尽可能结合先验知 识,找到和样本数据 D 拟合最好的网络结构。 测试 网络结构与样本集匹配程度的函数称为评分函数。 本文采用基于贝叶斯统计思想的贝叶斯评分函数: P(D | S) = ∏ n i = 1 ∏ qij j = 1 Γ αij ( ) Γ αij + Nij ( ) ∏ r i k = 1 Γ αijk + Nijk ( ) Γ αijk ( ) (2) 式中: Nijk 是 D 中满足 xi = k、Pa xi ( ) = j 的样本个数, Nij = ∑ r i k = 1 Nijk,αij = ∑ r i k = 1 αijk ,取一个等价样本,其数量 为 N, αijk = N qi ri 。 2 人工蜂群算法原理 ABC 算法中,蜜源的位置表示问题的候选解, 花蜜数量反映解的质量。 最优蜜源的确定依靠人工 蜂群的迭代搜索。 人工蜂群包括 3 类:引领蜂、跟随 蜂和侦查蜂。 引领蜂标记较优蜜源,并将信息传递 给跟随蜂,跟随蜂根据蜜源的花蜜数量选择蜜源进 行更新,侦查蜂随机搜索新蜜源。 设在 D 维空间中,种群规模为 2×SN(引领蜂个 数=跟随蜂个数 = SN),蜜源与引领蜂一一对应,即 蜜源 数 目 为 SN, 第 i 个 蜜 源 的 位 置 记 为 Xi = xi1 ,xi2 ,…,xiD ( ) 。 算法的迭代过程中,跟随蜂根据 引领蜂分享的信息,以轮盘赌的方式根据式(3) 选 择一个蜜源: Pi = fit i ∑ SN j = 1 fit j (3) 式中: fit i 是花蜜数量(适应度),按照式(4)计算: fit i = 1 1 + f i ,f i ≥ 0 1 + abs f i ( ) ,f i < 0 ì î í ï ï ïï (4) 式中 f i 是第 i 个解的目标函数值。 引领 蜂 和 跟 随 蜂 按 照 式 ( 5 ) 由 蜜 源 Xi = xi1 ,xi2 ,…,xiD ( ) 得到新蜜源: vij = xij + r × xij - xkj ( ) (5) 式中: k ∈ {1,2,…,SN} 且 k ≠ i ; j ∈ {1,2,…,D} 是随机产生的整数; r ∈ [ - 1,1] 是一个随机数。 若在一定循环次数(limit)后,蜜源质量没有提高,则 引领蜂放弃该蜜源,转变为侦查蜂,按照式(6)随机 产生新蜜源: xij = l j + rand(0,1) × uj - l j ( ) (6) 式中: l j 和 uj 分别是变量 xij 的下界和上界。 3 人工蜂群算法的贝叶斯网络结构学习 ABC 算法中,学习最优贝叶斯网络结构的过程 就是蜂群寻找高收益蜜源的过程。 引领蜂能够保持 优良蜜源,有精英特性;跟随蜂能够增加较优蜜源对 应的蜜蜂数量,加速算法的收敛;侦查蜂任意搜索新 蜜源,增加了蜜源的多样性,有利于算法跳出局部最 优。 2 个过程的对应关系如表 1 所示。 表 1 2 个过程的对应关系 Table 1 The corresponding relation of the two processes 蜂群寻找蜜源过程 贝叶斯网络结构学习过程 蜜源位置 所有贝叶斯网络结构 蜜源的收益 贝叶斯网络的得分 高收益蜜源 最优贝叶斯网络结构 3.1 贝叶斯网络结构的编码 文中采用文献[17]中的矩阵编码方式,一个包 含 n 个节点的贝叶斯网络可以表示为 n × n 的矩阵 A = aij { } ,其中 aij 定义如下: aij = 1,j 是 i 的父节点 {0,否则 本文算法中表示贝叶斯网络结构的个体为 a11 a21…an1 a12 a22…an2…a1n a2n…ann 3.2 基于遗传算子的蜜源更新策略 人工蜂群算法一般用于解决连续优化问题,而 贝叶斯网络结构为二进制编码,因此不能直接应用 ABC 算法中式(5)产生新蜜源。 考虑式(5),实际上 是两个蜜源之间信息的分享以及个体蜜源自身特性 的继承,这类似于遗传算法中的交叉和变异算子,所 以采用交叉和变异两种算子对蜜源进行更新。 在交叉算子中,本文采用 rand 和 best 两种交叉 策略。 其中 rand 交叉策略是指随机选择一个蜜源 与待更新蜜源进行两点交叉,能够增强种群之间的 信息共享;best 交叉策略是指利用当前最优蜜源与 待更新蜜源进行两点交叉,有利于最优蜜源特性的 继承。 文中通过参数 p 来决定采取哪种交叉策略, p 的取值将在实验部分讨论。 在变异算子中,有加边、删边和反转边 3 种变异 操作。 本文通过随机均匀产生 1、2、3 的任意一个整 ·326· 智 能 系 统 学 报 第 9 卷
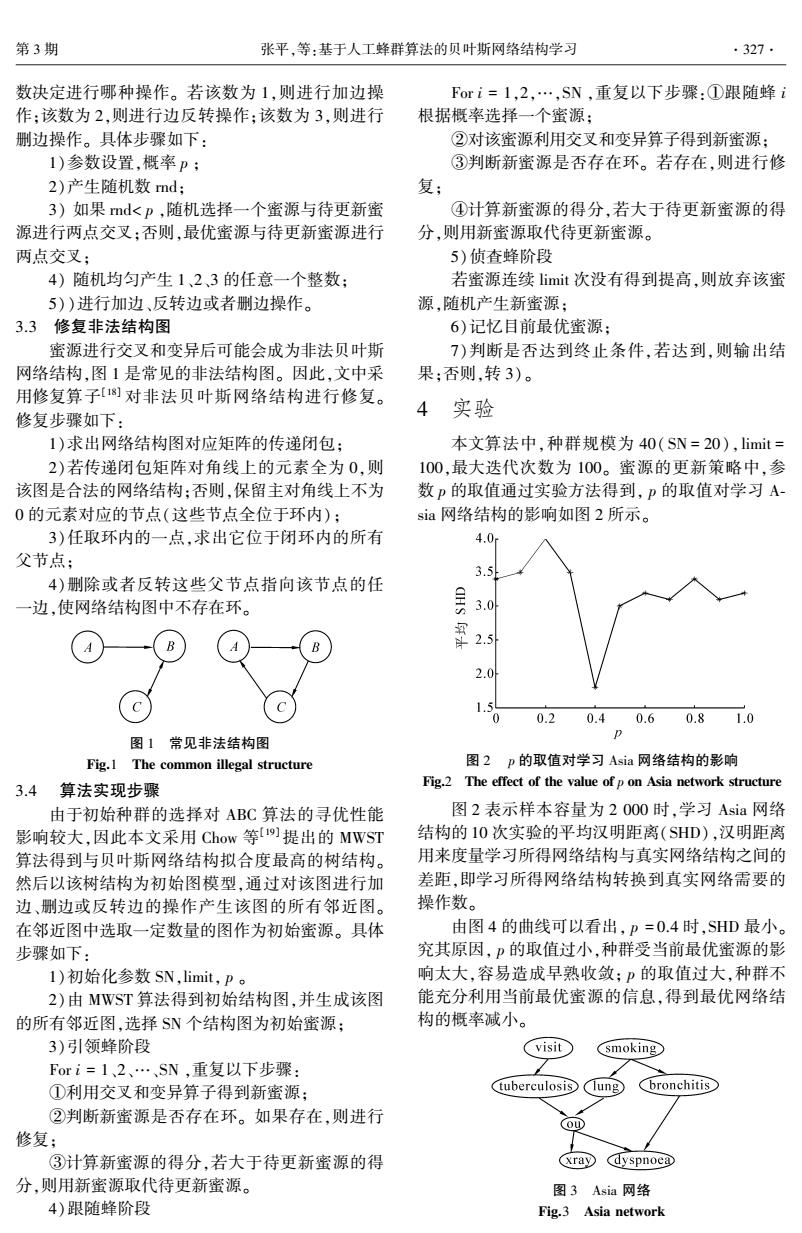
第3期 张平,等:基于人工蜂群算法的贝叶斯网络结构学习 .327. 数决定进行哪种操作。若该数为1,则进行加边操 Fori=1,2,…,SN,重复以下步骤:①跟随蜂i 作:该数为2,则进行边反转操作:该数为3,则进行 根据概率选择一个蜜源; 删边操作。具体步骤如下: ②对该蜜源利用交叉和变异算子得到新蜜源: 1)参数设置,概率p; ③判断新蜜源是否存在环。若存在,则进行修 2)产生随机数md; 复; 3)如果md<p,随机选择一个蜜源与待更新蜜 ④计算新蜜源的得分,若大于待更新蜜源的得 源进行两点交叉:否则,最优蜜源与待更新蜜源进行 分,则用新蜜源取代待更新蜜源。 两点交叉; 5)侦查蜂阶段 4)随机均匀产生1、2、3的任意一个整数: 若蜜源连续limit次没有得到提高,则放弃该蜜 5))进行加边、反转边或者删边操作。 源,随机产生新蜜源: 3.3修复非法结构图 6)记忆目前最优蜜源: 蜜源进行交叉和变异后可能会成为非法贝叶斯 7)判断是否达到终止条件,若达到,则输出结 网络结构,图1是常见的非法结构图。因此,文中采 果:否则,转3)。 用修复算子1]对非法贝叶斯网络结构进行修复。 修复步骤如下: 4实验 1)求出网络结构图对应矩阵的传递闭包; 本文算法中,种群规模为40(SN=20),limit= 2)若传递闭包矩阵对角线上的元素全为0,则 100,最大迭代次数为100。蜜源的更新策略中,参 该图是合法的网络结构:否则,保留主对角线上不为 数p的取值通过实验方法得到,p的取值对学习A- 0的元素对应的节点(这些节点全位于环内): sa网络结构的影响如图2所示。 3)任取环内的一点,求出它位于闭环内的所有 4.0 父节点; 3.5 4)删除或者反转这些父节点指向该节点的任 一边,使网络结构图中不存在环。 3.0 2.5 2.0 1.5 0 0.20.40.60.81.0 图1常见非法结构图 Fig.I The common illegal structure 图2p的取值对学习Asia网络结构的影响 3.4算法实现步骤 Fig.2 The effect of the value of p on Asia network structure 由于初始种群的选择对ABC算法的寻优性能 图2表示样本容量为2000时,学习Asia网络 影响较大,因此本文采用Chow等]提出的MWST 结构的10次实验的平均汉明距离(SHD),汉明距离 算法得到与贝叶斯网络结构拟合度最高的树结构。 用来度量学习所得网络结构与真实网络结构之间的 然后以该树结构为初始图模型,通过对该图进行加 差距,即学习所得网络结构转换到真实网络需要的 边、删边或反转边的操作产生该图的所有邻近图。 操作数。 在邻近图中选取一定数量的图作为初始蜜源。具体 由图4的曲线可以看出,p=0.4时,SHD最小。 步骤如下: 究其原因,p的取值过小,种群受当前最优蜜源的影 1)初始化参数SN,limit,p。 响太大,容易造成早熟收敛;p的取值过大,种群不 2)由MWST算法得到初始结构图,并生成该图 能充分利用当前最优蜜源的信息,得到最优网络结 的所有邻近图,选择SN个结构图为初始蜜源: 构的概率减小。 3)引领蜂阶段 visit smoking Fori=1、2、…、SN,重复以下步骤: ①利用交叉和变异算子得到新蜜源: tuberculosis Cung Cbronchitis ②判断新蜜源是否存在环。如果存在,则进行 00 修复; ③计算新蜜源的得分,若大于待更新蜜源的得 xray dyspnoea 分,则用新蜜源取代待更新蜜源。 图3Asia网络 4)跟随蜂阶段 Fig.3 Asia network
数决定进行哪种操作。 若该数为 1,则进行加边操 作;该数为 2,则进行边反转操作;该数为 3,则进行 删边操作。 具体步骤如下: 1)参数设置,概率 p ; 2)产生随机数 rnd; 3) 如果 rnd< p ,随机选择一个蜜源与待更新蜜 源进行两点交叉;否则,最优蜜源与待更新蜜源进行 两点交叉; 4) 随机均匀产生 1、2、3 的任意一个整数; 5))进行加边、反转边或者删边操作。 3.3 修复非法结构图 蜜源进行交叉和变异后可能会成为非法贝叶斯 网络结构,图 1 是常见的非法结构图。 因此,文中采 用修复算子[18] 对非法贝叶斯网络结构进行修复。 修复步骤如下: 1)求出网络结构图对应矩阵的传递闭包; 2)若传递闭包矩阵对角线上的元素全为 0,则 该图是合法的网络结构;否则,保留主对角线上不为 0 的元素对应的节点(这些节点全位于环内); 3)任取环内的一点,求出它位于闭环内的所有 父节点; 4)删除或者反转这些父节点指向该节点的任 一边,使网络结构图中不存在环。 图 1 常见非法结构图 Fig.1 The common illegal structure 3.4 算法实现步骤 由于初始种群的选择对 ABC 算法的寻优性能 影响较大,因此本文采用 Chow 等[19] 提出的 MWST 算法得到与贝叶斯网络结构拟合度最高的树结构。 然后以该树结构为初始图模型,通过对该图进行加 边、删边或反转边的操作产生该图的所有邻近图。 在邻近图中选取一定数量的图作为初始蜜源。 具体 步骤如下: 1)初始化参数 SN,limit, p 。 2)由 MWST 算法得到初始结构图,并生成该图 的所有邻近图,选择 SN 个结构图为初始蜜源; 3)引领蜂阶段 For i = 1、2、…、SN ,重复以下步骤: ①利用交叉和变异算子得到新蜜源; ②判断新蜜源是否存在环。 如果存在,则进行 修复; ③计算新蜜源的得分,若大于待更新蜜源的得 分,则用新蜜源取代待更新蜜源。 4)跟随蜂阶段 For i = 1,2,…,SN ,重复以下步骤:①跟随蜂 i 根据概率选择一个蜜源; ②对该蜜源利用交叉和变异算子得到新蜜源; ③判断新蜜源是否存在环。 若存在,则进行修 复; ④计算新蜜源的得分,若大于待更新蜜源的得 分,则用新蜜源取代待更新蜜源。 5)侦查蜂阶段 若蜜源连续 limit 次没有得到提高,则放弃该蜜 源,随机产生新蜜源; 6)记忆目前最优蜜源; 7)判断是否达到终止条件,若达到,则输出结 果;否则,转 3)。 4 实验 本文算法中,种群规模为 40( SN = 20),limit = 100,最大迭代次数为 100。 蜜源的更新策略中,参 数 p 的取值通过实验方法得到, p 的取值对学习 A⁃ sia 网络结构的影响如图 2 所示。 图 2 p 的取值对学习 Asia 网络结构的影响 Fig.2 The effect of the value of p on Asia network structure 图 2 表示样本容量为 2 000 时,学习 Asia 网络 结构的 10 次实验的平均汉明距离(SHD),汉明距离 用来度量学习所得网络结构与真实网络结构之间的 差距,即学习所得网络结构转换到真实网络需要的 操作数。 由图 4 的曲线可以看出, p = 0.4 时,SHD 最小。 究其原因, p 的取值过小,种群受当前最优蜜源的影 响太大,容易造成早熟收敛; p 的取值过大,种群不 能充分利用当前最优蜜源的信息,得到最优网络结 构的概率减小。 图 3 Asia 网络 Fig.3 Asia network 第 3 期 张平,等:基于人工蜂群算法的贝叶斯网络结构学习 ·327·

.328. 智能系统学报 第9卷 习,并与贪婪算法(GS)和爬山算法(HC)进行 Battery Age StarterFuelPump)FuelLine Fuel Spark 比较。为了保证3种算法在相同的实验条件下 进行,3种算法均采用MWST算法得到初始结 Battery CFuelSubsys Gauge 构图,在不同样本数据集上分别独立运行10 次。测试结果如表2和表3所示,其中A(G)表 Lights TurnsOver Starts 示学习所得的网络结构中额外增加的边数;D 图4Car网络 (G)表示学习所得的网络结构中丢掉的边数:1 Fig.4 Car network (G)表示学习所得的网络结构中错误指向的边 为检验算法应用于贝叶斯网络结构学习的 数;Score表示网络结构的得分值。3种算法对 有效性,对经典的Asia和Car网络进行结构学 Asia网络和Car网络的学习结果如表2和表3。 表23种算法对Asia网络的学习结果 Table 2 Learning results of the three algorithms for Asia network 1000 1500 2000 算法 A(G) D(G) K(G) A(G) D(G) KG) A(G) D(G) K(G) ABC-BN 0.5 1.0 1.0 0.5 1.0 0.5 0 1.0 0.4 GS 0.8 1.0 1.7 0.7 1.0 1.5 0.8 1.0 1.0 HC 0.8 1.0 1.6 0.8 1.0 1.5 0.6 1.0 1.0 表3 3种算法对Car网络的学习结果 Table 3 Learning results of the three algorithms for Car network 1000 1500 2000 算法 A(G) D(G) K(G) A(G) D(G) KG) A(G) D(G) I(G) ABC-BN 0.6 1.0 1.4 0.5 1.0 1.0 0.4 1.0 0.5 GS 1.8 1.2 1.7 1.3 1.0 1.2 0.9 1.0 1.1 HC 1.8 1.0 1.5 1.5 1.0 1.3 0.6 1.2 1.0 由表2、3的数据可以看出,在样本容量相同能算法的种群规模均为40。最大迭代次数为 的情况下,ABC-BN算法得到的网络结构最接近 100。表4列出了3种算法学习Asia网络的有效 真实的网络结构,而GS和HC算法得到的网络收敛时间和相应的得分。实验中,每种算法独立 结构错误边数相对较多。这说明了ABC-BN算运行10次,取平均值。由表4的数据可以看出, 法的有效性。 ABC-BN算法得到的网络结构得分最高且有效收 为了说明ABC-BN算法的学习性能。将本文敛时间最短。由此证明了ABC-BN算法能较快 算法与智能算法GA和HPGA-BN[1⑧]比较。各智地收敛到高精度的解。 表43种算法学习Asia网络的结果比较 Table 4 Comparison of the results of the three algorithms for learning Asia network 样本 GA HPGA-BN ABC-BN 容量 得分值 时间/s 得分值 时间/s 得分值 时间/s 1000 -2292.48 8.16 -2281.02 6.54 -2280.24 3.21 1500 -3457.10 8.83 -3446.14 7.28 -3444.18 3.85 2000 -4523.61 9.14 -4515.42 7.90 -4515.00 4.02 5 结束语 步的研究方向是在样本容量较小的情况下,通过设计 更有效的操作算子得到质量较高的网络结构。 本文提出一种基于遗传算子的人工蜂群算法。 该算法将遗传算子嵌入到人工蜂群算法中,并成功应 参考文献: 用于贝叶斯网络结构学习问题。实验结果表明,该算 [1]CAI Z,SUN S,SI S,et al.Identifying product failure rate 法具有较快的收敛速率和较高的学习质量。在实际 based on a conditional Bayesian network classifier[J].Expert 应用中,往往得不到容量较大的样本数据,所以,下一 Systems with Applications,2011,38(5):5036-5043 2]HSIEH N C.HUNG L P.A data driven ensemble classifier
图 4 Car 网络 Fig.4 Car network 为检验算法应用于贝叶斯网络结构学习的 有效性,对经典的 Asia 和 Car 网络进行结构学 习,并与贪婪算法 ( GS) 和 爬 山 算 法 ( HC) 进 行 比较。 为了保证 3 种算法在相同的实验条件下 进行,3 种 算 法 均 采 用 MWST 算 法 得 到 初 始 结 构图,在 不 同 样 本 数 据 集 上 分 别 独 立 运 行 10 次。 测试结果如表 2 和表 3 所示,其中 A( G) 表 示学习所 得 的 网 络 结 构 中 额 外 增 加 的 边 数; D ( G) 表示学习所得的网络结构中丢掉的边数; I ( G) 表示学习所得的网络结构中错误指向的边 数;Score 表示网络结构的得分值。 3 种算法对 Asia 网络和 Car 网络的学习结果如表 2 和表 3。 表 2 3 种算法对 Asia 网络的学习结果 Table 2 Learning results of the three algorithms for Asia network 算法 1 000 A( G) D( G) I( G) 1 500 A( G) D( G) I( G) 2 000 A( G) D( G) I( G) ABC⁃BN 0.5 1.0 1.0 0.5 1.0 0.5 0 1.0 0.4 GS 0.8 1.0 1.7 0.7 1.0 1.5 0.8 1.0 1.0 HC 0.8 1.0 1.6 0.8 1.0 1.5 0.6 1.0 1.0 表 3 3 种算法对 Car 网络的学习结果 Table 3 Learning results of the three algorithms for Car network 算法 1 000 A( G) D( G) I( G) 1 500 A( G) D( G) I( G) 2 000 A( G) D( G) I( G) ABC⁃BN 0.6 1.0 1.4 0.5 1.0 1.0 0.4 1.0 0.5 GS 1.8 1.2 1.7 1.3 1.0 1.2 0.9 1.0 1.1 HC 1.8 1.0 1.5 1.5 1.0 1.3 0.6 1.2 1.0 由表 2、3 的数据可以看出,在样本容量相同 的情况下,ABC⁃BN 算法得到的网络结构最接近 真实的网 络 结 构,而 GS 和 HC 算 法 得 到 的 网 络 结构错误 边 数 相 对 较 多。 这 说 明 了 ABC⁃BN 算 法的有效性。 为了说明 ABC⁃BN 算法的学习性能。 将本文 算法与智能算法 GA 和 HPGA⁃BN [ 18] 比较。 各智 能算 法 的 种 群 规 模 均 为 40。 最 大 迭 代 次 数 为 100。 表 4 列出了 3 种算法学习 Asia 网络的有效 收敛时间和相应的得分。 实验中,每种算法独立 运行 10 次,取平均值。 由表 4 的数据可以看出, ABC⁃BN 算法得到的网络结构得分最高且有效收 敛时间最 短。 由 此 证 明 了 ABC⁃BN 算 法 能 较 快 地收敛到高精度的解。 表 4 3 种算法学习 Asia 网络的结果比较 Table 4 Comparison of the results of the three algorithms for learning Asia network 样本 容量 GA 得分值 时间/ s HPGA⁃BN 得分值 时间/ s ABC⁃BN 得分值 时间/ s 1 000 -2 292.48 8.16 -2 281.02 6.54 -2 280.24 3.21 1 500 -3 457.10 8.83 -3 446.14 7.28 -3 444.18 3.85 2 000 -4 523.61 9.14 -4 515.42 7.90 -4 515.00 4.02 5 结束语 本文提出一种基于遗传算子的人工蜂群算法。 该算法将遗传算子嵌入到人工蜂群算法中,并成功应 用于贝叶斯网络结构学习问题。 实验结果表明,该算 法具有较快的收敛速率和较高的学习质量。 在实际 应用中,往往得不到容量较大的样本数据,所以,下一 步的研究方向是在样本容量较小的情况下,通过设计 更有效的操作算子得到质量较高的网络结构。 参考文献: [1]CAI Z, SUN S, SI S, et al. Identifying product failure rate based on a conditional Bayesian network classifier[J]. Expert Systems with Applications, 2011, 38(5): 5036⁃5043. [2]HSIEH N C, HUNG L P. A data driven ensemble classifier ·328· 智 能 系 统 学 报 第 9 卷

第3期 张平,等:基于人工蜂群算法的贝叶斯网络结构学习 ·329. for credit scoring analysis[J].Expert Systems with Applica- algorithm for neural network training[C]//2011 IEEE Con- tions,2010,37(1):534-545. gress on Evolutionary Computation.New Orleans,LA:IEEE [3]De CAMPOS L M.Independency relationships and learning Press,2011:84-88. algorithms for singly connected networks[J].Journal of Ex-[16]ABACHIZADEH M,YAZDI M,YOUSEFI-KOMA A.Opti- perimental Theoretical Artificial Intelligence,1998,10 mal tuning of PID controllers using artificial bee colony algo- (4):511-549. rithm[C]//2010 IEEE/ASME International Conference on [4]De CAMPOS L M HUETE J F.A new approach for learning Advanced Intelligent.Montreal:IEEE Press,2010:379- belief networks using independence criteria[J].Interational 384. Journal of Approximate Reasoning,2000,24(1):11-37.[17]LARRANAGA P,POZA M,YURRAMENDI Y.et al. [5]COOPER G F,HERSKOVITS E.A Bayesian method for the Structure learning of Bayesian networks by genetic algo- induction of probabilistic networks from data[J].Machine rithms:a performance analysis of control parameters[J]. Learning,1992,9(4):309-347. IEEE Transactions on Pattem Analysis and Machine Intelli- [6]HECKERMAN D,GEIGER D,CHICKERING D M.Learning gence,1996,18(9):912-926. Bayesian networks:The combination of knowledge and statis-[l8]许丽佳,黄建国,王厚军,等.混合优化的贝叶斯网络结 tical data[J].Machine Learning,1995,20(3):197-243. 构学习[J].计算机辅助设计与图形学报,2009,21(5): [7]LAM W,BACCHUS F.Learning Bayesian belief networks: 633-639. an approach based on the MDL principle[J].Computational XU Lijia,HUANG Jianguo,WANG Houjun,et al.Hybrid Intelligence,1994,10(3):269-293. optimized algorithm for learning Bayesian network structure [8]COOPER G F,HERSKOVITS E.A Bayesian method for the []Journal of Computer-Aided Design Computer Graph- induction of probabilistic networks from data[J.Machine ics,2009,21(5):633-639. Learning,1992,9(4):309-347. [19]CHOW C,LIU C.Approximation discrete probability distri- [9 CHICKERING D M.Optimal structure identification with butions with dependence trees[J].IEEE Transactions on In- greedy search[J].The Journal of Machine Learning Re- formation Theory,1968,14(3):462-467. 8 earch,2003(3):507-554. 作者简介: [10]KARABOGA D.An idea based on honey bee swarm for nu- 张平,女,1988年生,硕士研究生,主 merical optimization[R].Erciyes university,engineering 要研究方向为优化算法、贝叶斯网络结 faculty,computer engineering department,2005. 构学习。 [11]KARABOGA D,BASTURK B.A powerful and efficient al- gorithm for numerical function optimization:artificial bee colony (ABC)algorithm[J].Journal of Global Optimiza- 刘三阳,男,1959年生,教授.博士生 tion,2007,39(3):459-471. [12]KARABOGA D,BASTURK B.On the performance of artifi- 导师,主要研究方向为优化理论及其应 cial bee colony (ABC)algorithm[J].Applied soft Compu- 用、网络算法。主持多项国家级项目,发 ting,2008,8(1):687-697. 表多篇学术论文。 [13]KARABOGA D.AKAY B.Artificial bee colony (abc)algo- rithm on training artificial neural networks[C]//2007 IEEE 朱明敏,女,1985年生,讲师,博士 15th Signal Processing and Communications Applications. Eskisehir:IEEE Press,2007:1-4. 后,主要研究方向为优化算法及其在贝 叶斯网络结构学习中的应用。 [14]KARABOGA D,OZTURK C.Neural networks training by artificial bee colony algorithm on pattern classification[J]. Neural Netw World,2009,19(3):279-292. [15]OZTURK C,KARABOGA D.Hybrid artificial bee colony
for credit scoring analysis[ J]. Expert Systems with Applica⁃ tions, 2010, 37(1): 534⁃545. [3]De CAMPOS L M . Independency relationships and learning algorithms for singly connected networks[ J]. Journal of Ex⁃ perimental & Theoretical Artificial Intelligence, 1998, 10 (4): 511⁃549. [4]De CAMPOS L M , HUETE J F. A new approach for learning belief networks using independence criteria[ J]. International Journal of Approximate Reasoning, 2000, 24(1): 11⁃37. [5]COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data [ J]. Machine Learning, 1992, 9(4): 309⁃347. [6]HECKERMAN D, GEIGER D, CHICKERING D M. Learning Bayesian networks: The combination of knowledge and statis⁃ tical data[J]. Machine Learning, 1995, 20(3): 197⁃243. [7] LAM W, BACCHUS F. Learning Bayesian belief networks: an approach based on the MDL principle[ J]. Computational Intelligence, 1994, 10(3): 269⁃293. [8]COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data [ J]. Machine Learning, 1992, 9(4): 309⁃347. [ 9 ] CHICKERING D M. Optimal structure identification with greedy search [ J]. The Journal of Machine Learning Re⁃ search, 2003(3): 507⁃554. [10]KARABOGA D. An idea based on honey bee swarm for nu⁃ merical optimization [ R]. Erciyes university, engineering faculty, computer engineering department, 2005. [11]KARABOGA D, BASTURK B. A powerful and efficient al⁃ gorithm for numerical function optimization: artificial bee colony ( ABC) algorithm [ J]. Journal of Global Optimiza⁃ tion, 2007, 39(3): 459⁃471. [12]KARABOGA D, BASTURK B. On the performance of artifi⁃ cial bee colony (ABC) algorithm[ J]. Applied soft Compu⁃ ting, 2008, 8(1): 687⁃697. [13]KARABOGA D, AKAY B. Artificial bee colony (abc) algo⁃ rithm on training artificial neural networks[C] / / 2007 IEEE 15th Signal Processing and Communications Applications. Eskisehir: IEEE Press, 2007: 1⁃4. [14] KARABOGA D, OZTURK C. Neural networks training by artificial bee colony algorithm on pattern classification[ J]. Neural Netw World, 2009, 19(3): 279⁃292. [15]OZTURK C, KARABOGA D. Hybrid artificial bee colony algorithm for neural network training[C] / / 2011 IEEE Con⁃ gress on Evolutionary Computation. New Orleans, LA:IEEE Press, 2011: 84⁃88. [16]ABACHIZADEH M, YAZDI M, YOUSEFI⁃KOMA A. Opti⁃ mal tuning of PID controllers using artificial bee colony algo⁃ rithm[ C] / / 2010 IEEE/ ASME International Conference on Advanced Intelligent. Montreal: IEEE Press, 2010: 379⁃ 384. [17] LARRANAGA P, POZA M, YURRAMENDI Y. et al. Structure learning of Bayesian networks by genetic algo⁃ rithms: a performance analysis of control parameters[ J]. IEEE Transactions on Pattern Analysis and Machine Intelli⁃ gence, 1996, 18(9): 912⁃926. [18]许丽佳, 黄建国, 王厚军, 等. 混合优化的贝叶斯网络结 构学习[J]. 计算机辅助设计与图形学报, 2009, 21(5): 633⁃639. XU Lijia, HUANG Jianguo, WANG Houjun, et al. Hybrid optimized algorithm for learning Bayesian network structure [J]. Journal of Computer⁃Aided Design & Computer Graph⁃ ics, 2009, 21(5): 633⁃639. [19]CHOW C, LIU C. Approximation discrete probability distri⁃ butions with dependence trees[J]. IEEE Transactions on In⁃ formation Theory, 1968, 14(3): 462⁃467. 作者简介: 张平,女,1988 年生,硕士研究生,主 要研究方向为优化算法、贝叶斯网络结 构学习。 刘三阳,男,1959 年生,教授,博士生 导师,主要研究方向为优化理论及其应 用、网络算法。 主持多项国家级项目,发 表多篇学术论文。 朱明敏,女, 1985 年生,讲师,博士 后, 主要研究方向为优化算法及其在贝 叶斯网络结构学习中的应用。 第 3 期 张平,等:基于人工蜂群算法的贝叶斯网络结构学习 ·329·