
生物大分子波谱学原理 吴季辉 与CBHP关联的三共振实验 已经讨论过的三共振实验涉及主链上的连接关系,而HCCH 类型的实验提供了氨基酸侧链上的连接,将二者结合起来可 以获得完整的证认信息。虽然二者的连接点在H或13C, 但由于这两种核的化学位移分布范围不大,不利于谱峰的解 析,更好的是利用HN及15N。因此产生出两类实验:一类利 用COSY原理将信号传递至13Ca,再进一步传递至15N及1HN, 这类实验有CBCA(CO)NH,CBCANH, HBHA(CBCACO)NH,HBHA(CBCA)NH;另一类实验利用 TOCSY将信号传递至3C,再进一步传递至15N及HN,这类 实验有C(CO)NH-TOCSY,H(C)(CO)NH-TOCSY。由于这些 实验涉及侧链,侧链碳骨架的形式对信号的传递效率有很大 影响。另一方面所得信息也可提供侧链类型即残基类型的信 息
与C /H关联的三共振实验 生物大分子波谱学原理 吴季辉 已经讨论过的三共振实验涉及主链上的连接关系,而HCCH 类型的实验提供了氨基酸侧链上的连接,将二者结合起来可 以获得完整的证认信息。虽然二者的连接点在1H或13C , 但由于这两种核的化学位移分布范围不大,不利于谱峰的解 析,更好的是利用1HN及15N。因此产生出两类实验:一类利 用COSY原理将信号传递至13C ,再进一步传递至15N及1HN , 这类实验有CBCA(CO)NH,CBCANH, HBHA(CBCACO)NH,HBHA(CBCA)NH;另一类实验利用 TOCSY将信号传递至13C ,再进一步传递至15N及1HN ,这类 实验有C(CO)NH-TOCSY,H(C)(CO)NH-TOCSY。由于这些 实验涉及侧链,侧链碳骨架的形式对信号的传递效率有很大 影响。另一方面所得信息也可提供侧链类型即残基类型的信 息

生物大分子波谐学原理 吴季辉 CBCACONH H-C- CBCA(CONH H
CBCA(CO)NH 生物大分子波谱学原理 吴季辉
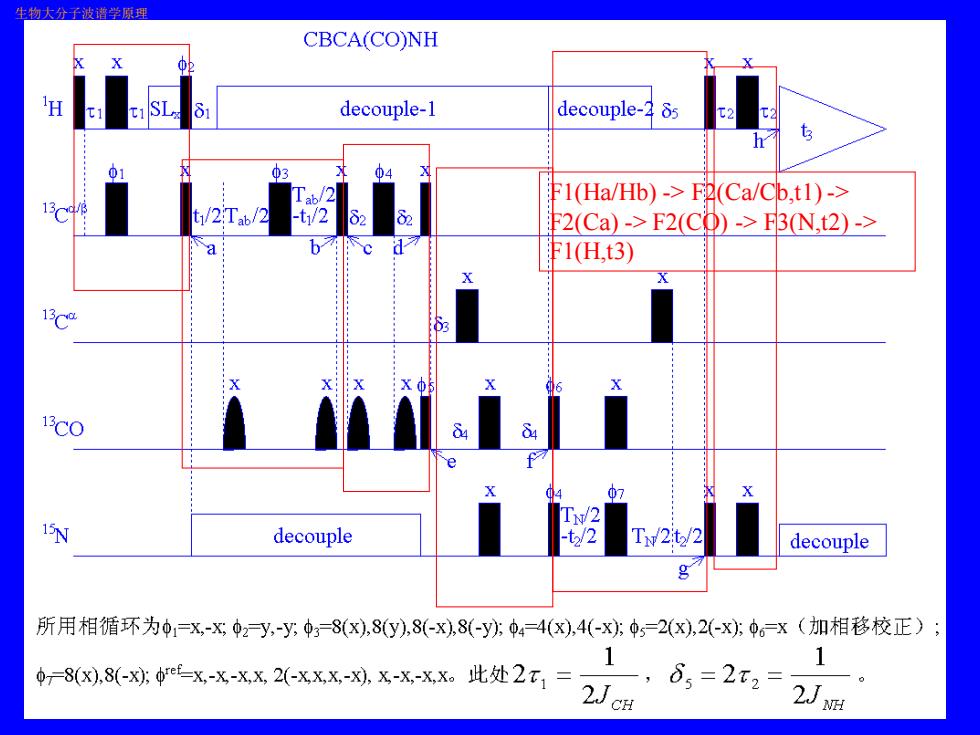
生物大分子波谱学原理 CBCA(CO)NH decouple-1 decouple-2 85 2 03 F1(Ha/Hb)->F2(Ca/Cb,t1)-> 139 2Tab /2 2(Ca)->F2(Cp)->F3N,t2)-> F1(Ht3) 13C X O 6 13C0 07 X Ty/2 1 decouple -t2/2 Ty2t/2 decouple g 所用相循环为中=x,-Xφ2y,-y,中8(X),8(y),8(-X),8(-y中44(X),4(-x;-2(),2(-x。=x(加相移校正); 1 1 =8(x),8(-x:e=X-X-X,X,2(-xxX-X),X-X,-X,X。此处2T1= 2Jc用 6,=2x2=
CBCA(CO)NH 生物大分子波谱学原理 吴季辉 F1(Ha/Hb) -> F2(Ca/Cb,t1) -> F2(Ca) -> F2(CO) -> F3(N,t2) -> F1(H,t3)

生物大分子波增学原理 CBCA(CO)NH 吴季辉 decouple-I decouple- CBCA(CONH co decouple Liwii decouple 从1HH的信号出发,经过第一个NEPT,分别传递给13C13C: 8(-y以44(.4(-x=2,2(-x实=X〔加相移校正) o。=-2HgCg-2HBCS x此处2x= 6,=22J 在第一个恒时期间,13CP的信号通过J偶合形成相对13C的反相分量,通 常取TAB=6.6ms以优化二者间的传递: =C cos(h)cos(nIT)mI() +2CCcos()sin(Tco(TnI,( 此处b为13C核的数目,m为H的数目,g为13C核的数目,n为1H 的数目,δ1取2.2ms以优化Tm(61)和Tm(⑥1) 随后的13C90度脉冲对第一分量无影响,而使第二项发生相千转移: o。=C&cos(24)cos(πJcTA)mLm(6,) 2CC)sin(To(nT (
CBCA(CO)NH 生物大分子波谱学原理 吴季辉

生物大分子波谱学原理 CBCA(CO)NH 吴季辉 decouple-I decouple-48 CBCACONH decouple 接着282期间要建立相对13C0的反相磁化,同时会聚13C一13C间的反相 4(x),4(-x=2x,2(-x◆=X(加相移校正) 磁化: oa=2 C cos(2ce4)cos(πJCeTAB)mΓm(⑥,)r4(62) .6,=2=2J +2CCcos()sin(T)cos5 (Tn,(( 此处4(62)=cos(2mdec62)sin(2zdco62) T(2)=sin(2n/2)sin(2/2) 取δ2=3.7ms以优化二者 随后13C13CP及13C0的90度脉冲形成13C0相对13C的反相磁化: .=-2CC cos()cos(T)mI()) -2CC cos()sin()cos (/T)n (
CBCA(CO)NH 生物大分子波谱学原理 吴季辉
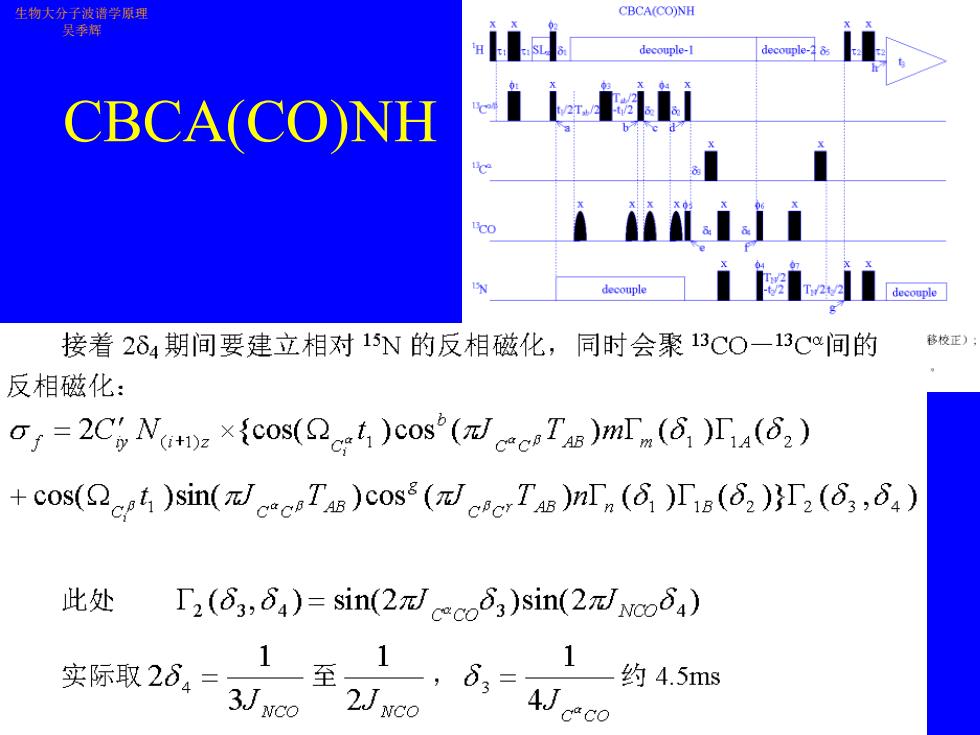
生物大分子波谐学原理 CBCA(CO)NH 吴季辉 decouple-1 CBCACONH co iiiliii decouple 接着264期间要建立相对15N的反相磁化,同时会聚13C0一13C间的 移校正); 反相磁化: o=2C NtDz xicos()cos (T)mIm ()Ta(62) +cos()sin()cos(Tn ()(,, 此处 2(⊙,d4)=sin(2 nco3)sin(2 No4) 实际取264= 1至,1,6=, 3J NCO 一约4.5ms 4J
CBCA(CO)NH 生物大分子波谱学原理 吴季辉

生物大分子波谱学原理 CBCA(CO)NH 吴季辉 decouple-I decouple-48 CBCA(CONH FCO N decouple decouple 所用相循环为:=X-xy,-y8x,8y),8(-x8(-y实:4(x),4(-x实=2x,2(-x◆=X(加相移校正) BC0及15N的90度脉冲产生极化转移,随后在第二个恒时期间,15N4xt处22 6,=22 演化并会聚相对3C0的反相磁化,同时建立相对H的反相磁化: =2HN xcos()cos'(nl T)mI () +cos()sin(T)cos(T)nT ()( x2(,6,)cos()sin(T) 通常TN取22ms左右 最后的会聚形成1H信号: oh=HYx{cos(2e4)cos(NcTAB)mm(⑥,)ⅡiA(62) +cos()sin(T)cos (T)nT (( (,)cos()sin(/)
CBCA(CO)NH 生物大分子波谱学原理 吴季辉
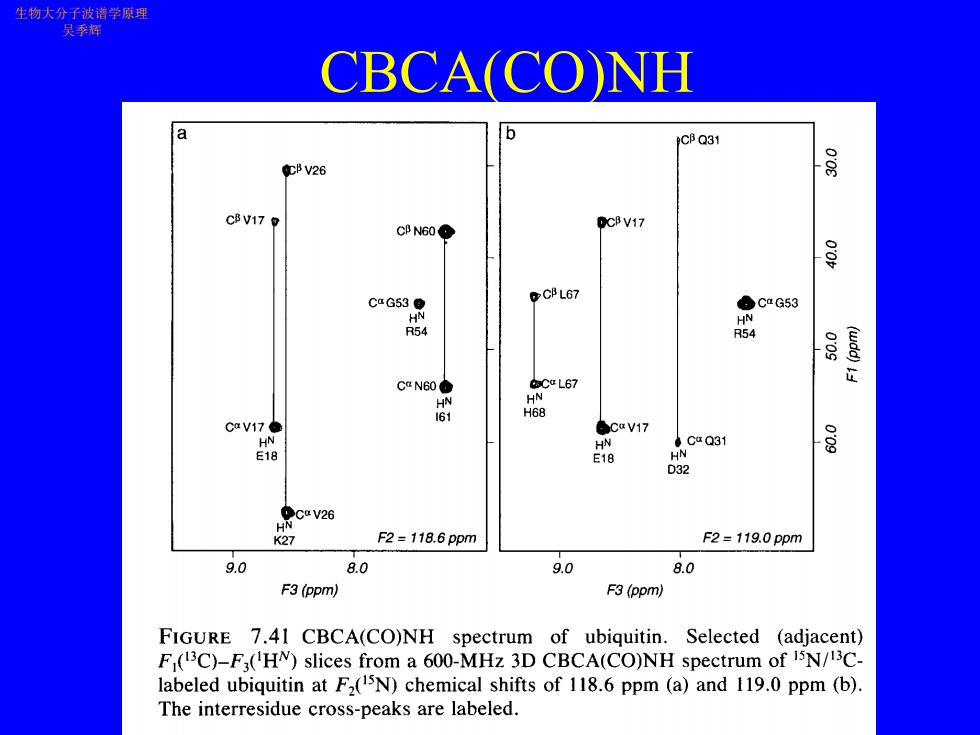
生物大分子波谱学原理 吴季辉 CBCA(CONH a CB Q31 CB V26 s CB V17 CBN6O◆ DCB V17 C CB L67 ●caG53 H R54 R54 惠 caN60 C L67 6 HN 68 CaV17● CaV17 HN Co Q31 品 E18 D32 caV26 HN 27 F2=118.6ppm F2=119.0ppm 9.0 8.0 9.0 8.0 F3(ppm) F3(ppm) FIGURE 7.41 CBCA(CO)NH spectrum of ubiquitin.Selected (adjacent) F(13C)-F3(HN)slices from a 600-MHz 3D CBCA(CO)NH spectrum of i5N/13C- labeled ubiquitin at F2(15N)chemical shifts of 118.6 ppm (a)and 119.0 ppm (b). The interresidue cross-peaks are labeled
CBCA(CO)NH 生物大分子波谱学原理 吴季辉
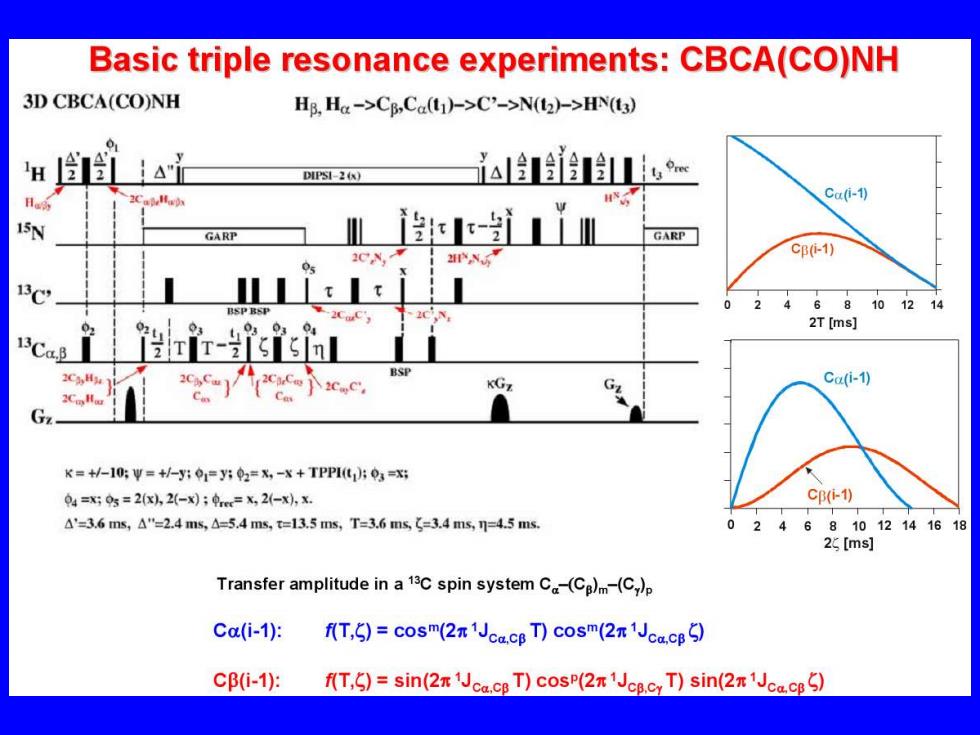
Basic triple resonance experiments:CBCA(CO)NH 3D CBCA(CO)NH Hg.Ha->CB,Ca(tj)->C'->N(t2)->HN(t3) △"1 DIPSI-2 (x) iali Ca(i-1) 15N GARP GARP CB-1) 13C 1: 2 BSPBSP 4681012 14 2T [ms] 2C3,H se-cce-)icsc. KGz G Ca(i-1) K=+/-10:"=+/-y:01=y52=X,-X+TPP1i03=x 04=x9g=2x2(-x刘;=x2(-x,x. C(作1) △'=3.6ms,△"=2.4ms,△-5.4ms,t=13.5ms,T=3.6ms,=3.4ms=4.5ms 024681012141618 2 [ms] Transfer amplitude in a 13C spin system C-(Ca)m-(C)p Ca(i-1): fT,)=cosm(2π1 Jca.cB)cosm(2π1 Jca.cp9 Ci-1: f(T,)=sin(2 Jca.ce T)cosP(2n1JcB.cyT)sin(2n 1Jca.cB5)
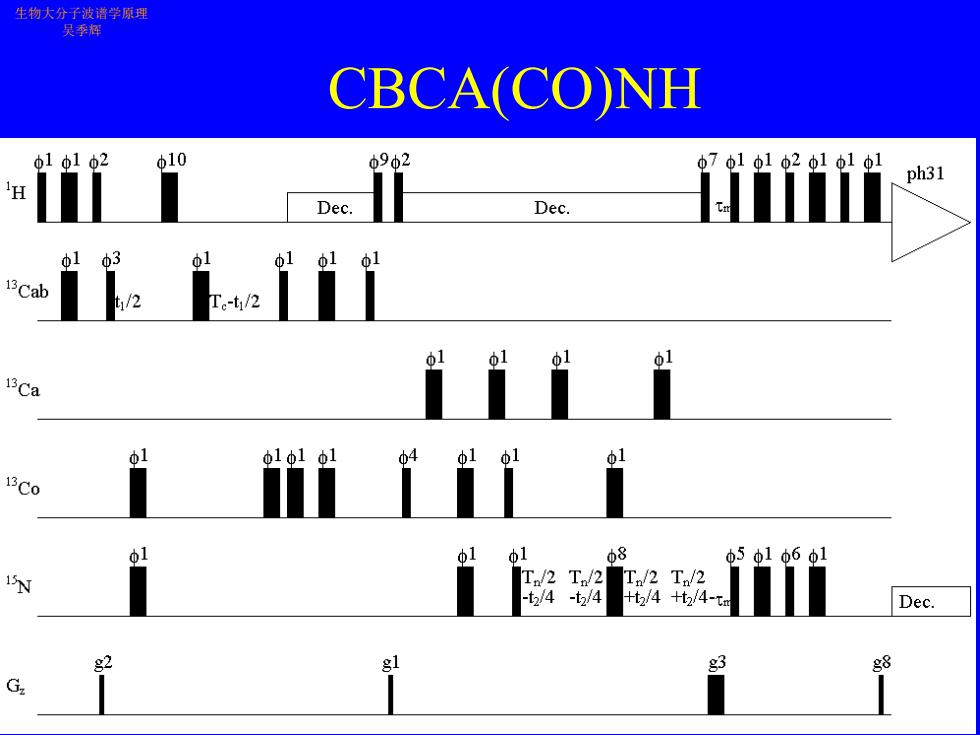
生物大分子波谐学原理 吴季辉 CBCA(CONH φ1Φ1Φ2 Φ10 09b2 07Φ1φ1φ2Φ1φ1φ1 ph31 H Dec. Dec. 01 1 13Cab /2 T.-t/2 61 1 1 13Ca 01 o101 o1 b101 13C0 91 Φ1 08 5φ1Φ61 N /2T/2 T/2 T/2 -t2/4 -t2/4 +t2/4+t2/4-t Dec. g2 gl g3 g8 G
CBCA(CO)NH 生物大分子波谱学原理 吴季辉