
第3章 化学反应概述 第3章 化学反概 上寿交通大学化学化工学限 3.2化学反应进行的方向 3.2.1基本概念 ·热力学: (1)体系和环境(system Surroundings - 研究热和其他形式能量间的转换规律的科学, and surroundings) 它研究某个体系发生变化时,引起体系的物 理量发生的变化。 ·被研究的物质体系(对象) 蓼·化学热力学: 称体系(系统); 第3 ·体系以外,与体系相联系 研究化学反应过程中能量转换与传递的科学。 化学反器 的部分称环境。 体系的分类: 体系的性质 热力学变量 我们的 ·量度性质(广延性质) 研究对象 具有加和性,如V,m 散开体系 封闭体系 孤立体系 第3章 (open (closed (isolated 第3章 ·强度性质 system) system) system) 物质交换 有 无 无 华 不具有加和性,如P,C 能量交换 有 有 无 反
1 第3章 化学反应概述 上海交通大学化学化工学院 大学化学教研室 第 3章化学反应概述 吸热反应 放热反应 Ba(OH)2·8H2O + 2NH4Cl(s)→BaCl2(s) + 2 NH3(aq) + 8 H2O(l) • 热力学: - 研究热和其他形式能量间的转换规律的科学, 它研究某个体系发生变化时,引起体系的物 理量发生的变化 第 3章化学反应概述 。 • 化学热力学: - 研究化学反应过程中能量转换与传递的科学。 3.2 化学反应进行的方向 3.2.1基本概念 (1)体系和环境(system and surroundings) 第 3章化学反应概述 • 被研究的物质体系(对象) 称体系(系统); • 体系以外,与体系相联系 的部分称环境。 体系的分类: 我们的 研究对象 第 3章化学反应概述 敞开体系 (open system) 封闭体系 (closed system) 孤立体系 (isolated system) 物质交换 有 无 无 能量交换 有 有 无 研究对象 体系的性质 热力学变量 • 量度性质(广延性质) 第 3章化学反应概述 具有加和性,如V, m • 强度性质 不具有加和性,如ρ, C
(2)状态和状态函数 状态函数的特征 (state and state function 1.状态函数:决定体系热力学状态的物理量称 为状态函数,如温度、压力、体积、密度等。 状态一定值一定; 2. 状态:热力学平衡状态,热平衡、力学平衡、 相平衡、化学平衡。 殊途同归变化等; 第3草 周而复始变为零。 化学反概送 两个例子 (3)过程和途径 (process and path) A途径 某气体 300K 350K △T=50K P:=50kPa ·350K △T=50K 350K △T=50K V,=4m3 300K 460K 350K 一300K △T=0K 始态 终态 改变量 P=100kPa P2=200kPa 始态 V,=2m3 V,=1m3 终态 化学 P.=400kPa 化学反应概述 V=0.5m3 B途径 热力学中常见的过程: (4)功和热(work and heat) 等温过程:体系的始态温度与终态温度相同,并等 于环境的温度:(T,=T2=T环) 热—热力学中把体系与环境之间因温差而 ·等压过程:始态、终态的压力与环境相同 变化的或传递的能量称为热,以Q表示 (P1=P2=P环) 体系吸热: ·等容过程:体系的体积不发生变化(V,=V2) ·绝热过程:体系与环境之间无热量交换(Q=0) 体系放热: ·循环过程:过程进行后,体系重新回到初始状态 (各种状态函数的增量为零)。 Endothermic Exothermic 自发过程:一定条件下,不需要外加能量就能够 System Q>0 Q<0 自动进行的过程。 Surroundings 2
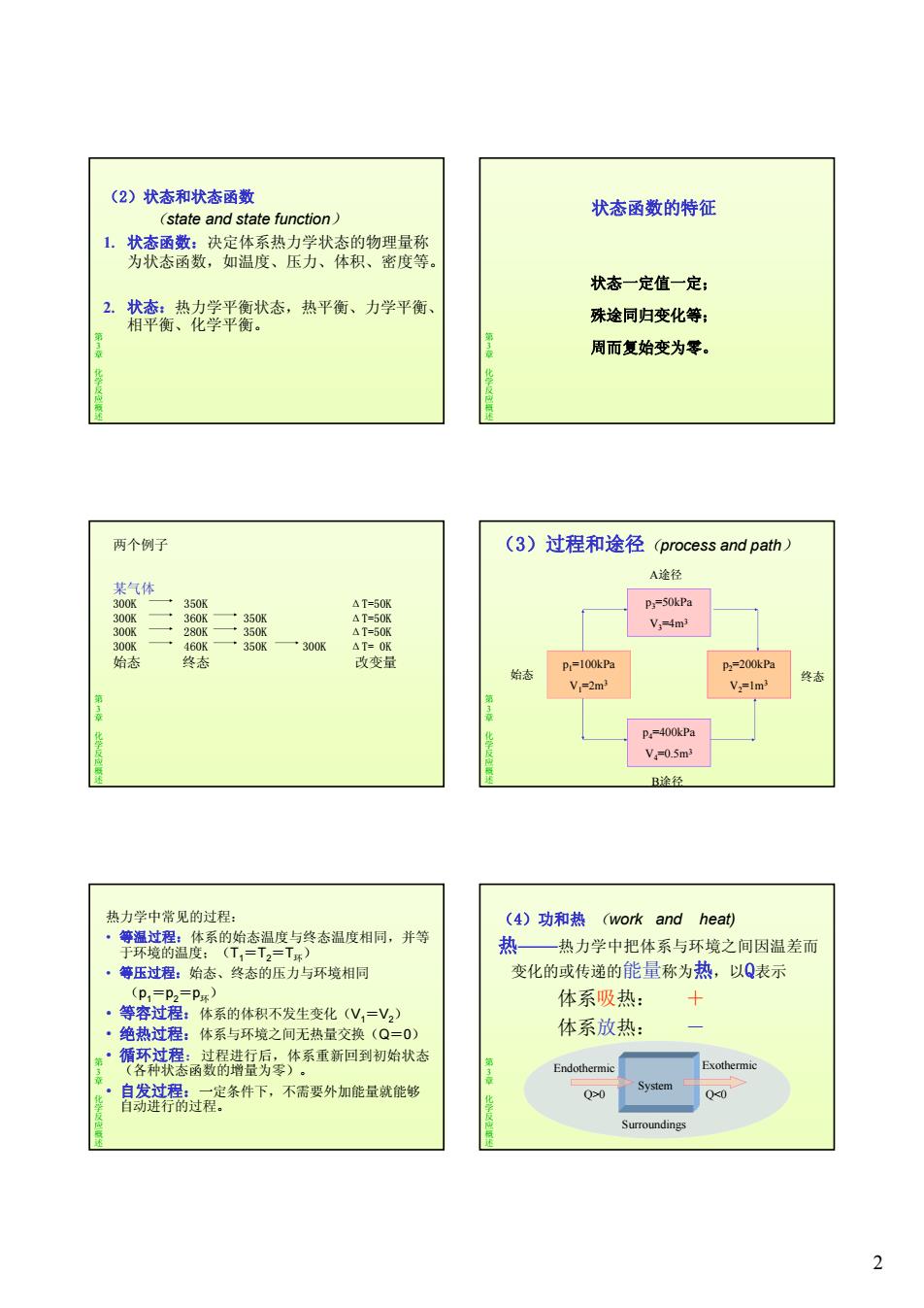
2 (2)状态和状态函数 (state and state function) 1. 状态函数:决定体系热力学状态的物理量称 为状态函数,如温度、压力、体积、密度等。 第 3章化学反应概述 2. 状态:热力学平衡状态,热平衡、力学平衡、 相平衡、化学平衡。 状态函数的特征 状态一定值一定; 第 3章化学反应概述 殊途同归变化等; 周而复始变为零。 某气体 300K 350K ΔT=50K 300K 360K 350K ΔT=50K 300K 280K 350K ΔT=50K 300K 460K 350K 300K ΔT= 0K 两个例子 第 3章化学反应概述 始态 终态 改变量 (3)过程和途径(process and path) p3=50kPa V3=4m3 A途径 第 3章化学反应概述 p2=200kPa V2=1m3 p1=100kPa V1=2m3 p4=400kPa V4=0.5m3 B途径 始态 终态 热力学中常见的过程: • 等温过程:体系的始态温度与终态温度相同,并等 于环境的温度;(T1=T2=T环) • 等压过程:始态、终态的压力与环境相同 (p1=p2=p环) • 等容过程:体系的体积不发生变化(V1=V2) 第 3章化学反应概述 等容过程:体系的体积不发生变化(V1 V2) • 绝热过程:体系与环境之间无热量交换(Q=0) • 循环过程:过程进行后,体系重新回到初始状态 (各种状态函数的增量为零)。 • 自发过程:一定条件下,不需要外加能量就能够 自动进行的过程。 (4)功和热 (work and heat) 热——热力学中把体系与环境之间因温差而 变化的或传递的能量称为热,以Q表示 体系吸热: + 第 3章化学反应概述 体系放热: - System Surroundings Q>0 Q<0 Endothermic Exothermic
功一体系与环境之间 leaves s work 除热以外,以其他形式交 换的能量都称为功,以丽 表示。 一膨胀功或体积功: -非体积功,用W表示 化学反感概述 膨胀功 Surroundings 0T1 ·功和热均以体系为参照背景 -w+w 体系吸热: 体系放热: 体系接受功: System 体系做出功: + Surroundings 第3草 ·功和热都是在状态变化过程中传递的能量,其 数值与状态变化的途径有关,故热、功不是状 化学反 C.H:N2+Cl-+H2O-C.H.OH+H++Cl+N2 化学反器 态函数,又称为过程函数。 状态函数与过程函数的关系之一 ·状态函数:状态一定值一定,其变化只 与体系变化过程的始态和终态有关,而与 方式或途径无关 ·过程函数:必与发生变化的具体途径有 关,伴随着途径而定 做功 不做功 状态函数过程函数 CaCo3=Ca0+CO2↑ 3
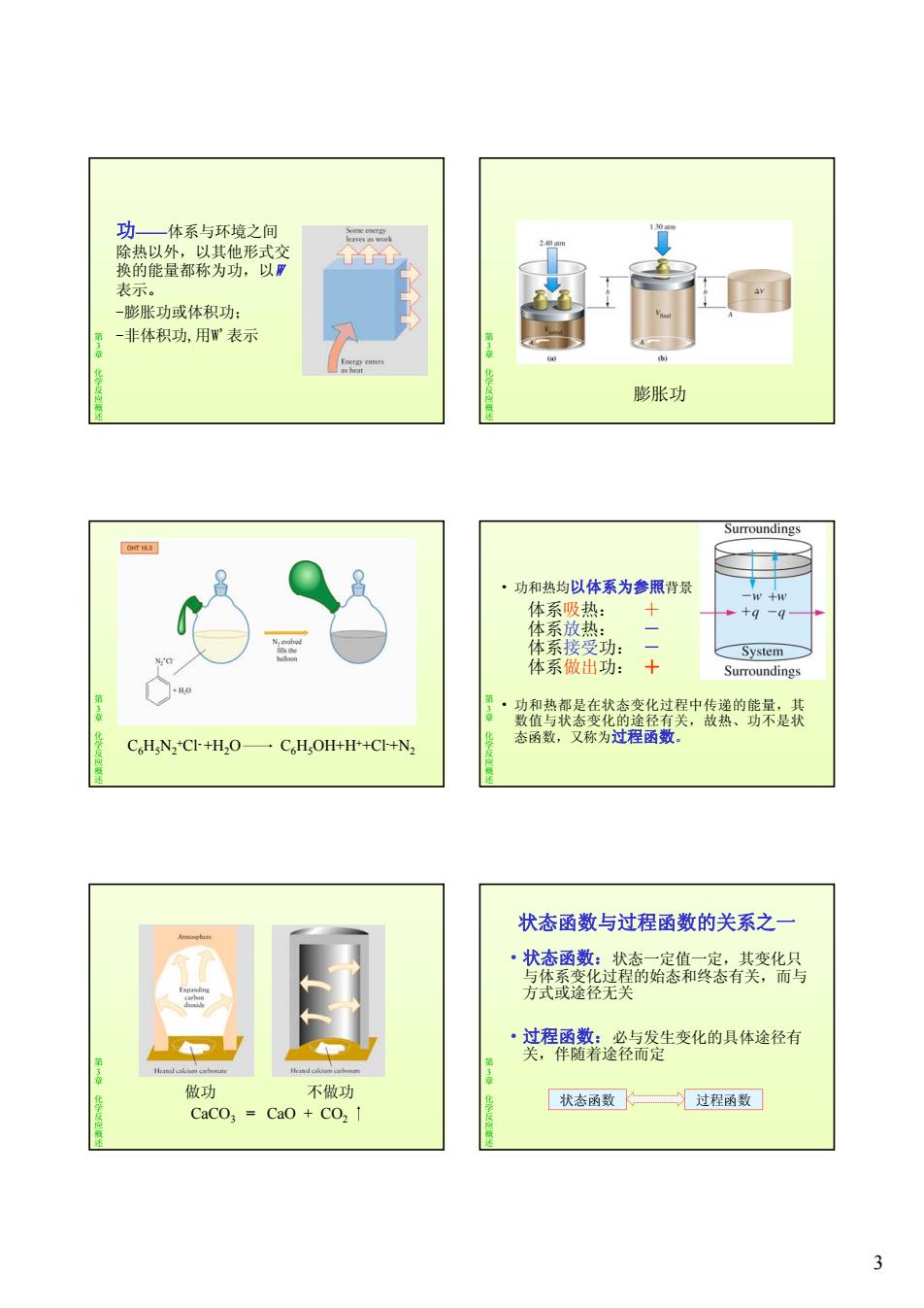
3 功——体系与环境之间 除热以外,以其他形式交 换的能量都称为功,以W 表示 第 3章化学反应概述 。 -膨胀功或体积功; -非体积功,用W'表示 第 3章化学反应概述 膨胀功 第 3章化学反应概述 C6H5N2 +Cl- +H2O C6H5OH+H++Cl- +N2 • 功和热均以体系为参照背景 体系吸热: + 体系放热: - 体系接受功: - 第 3章化学反应概述 体系接受功: 体系做出功: + • 功和热都是在状态变化过程中传递的能量,其 数值与状态变化的途径有关,故热、功不是状 态函数,又称为过程函数。 第 3章化学反应概述 做功 不做功 CaCO3 = CaO + CO2 状态函数与过程函数的关系之一 • 状态函数:状态一定值一定,其变化只 与体系变化过程的始态和终态有关,而与 方式或途径无关 第 3章化学反应概述 • 过程函数:必与发生变化的具体途径有 关,伴随着途径而定 状态函数 过程函数

(5)热力学能U(内能) 3.2.2热力学第一定律 [thermodynamic energy(internal energy)] 体系内部一切能量的总和: ·数学表达式:△U=Q一w a.分子或原子的位能、振动能、转动能、 =Q-PAV-W Turddand 平动能、电子的动能以及核能等。 b.绝对值无法测量或计算,只能计算AU。⊙心⑦ ·研究内容:体系变化过程中热力学能、功、 热的转换方式。 4理想气体的只是温度的函数,恒温过一人 c.U是体系的状态函数。 ·实质:能量守恒和转化定律。 章程△U=0。 能量的总量是守恒的,不会凭空产生,也不会凭空 e.具有加和性。 消失,只可能从一种形式转化为另一种形式。 化学反 在孤立体系中能量的总值恒定不变。 例:(1)某过程中,体系从环境吸收热量50kJ, 对环境做功30kJ。求过程中体系热力学能的改 变量△U和环境热力学能的改变量△U。 (2)如果开始时,体系先放热40kJ,环境 对体系做功60kJ,求体系的热力学能的改 解:由热力学第一定律的数学表达式可知 变量△U以及终态的热力学能U。 Q=+50kJ,=+30kJ 解:Q=-40kJ,F=-60kJ .4U体茶QM =50-30=20(kJ) 4U体系Q一F=20kJ UU1+20(kJ) 若将环境当做体系来考虑, 则有Q=-50kJ,=-30kJ, 故环境热力学能改变量4U'=Q'一W“ 化学反 ∴4U'环城-50-(-30)=-20(kJ) 讨论: 对于体系的始态U,和终态(U,+20), 3.2.3化学反应的热效应 虽然变化途径不同(Q、W不同),但△U却 1.化学反应热 相同。说明Q、W是非状态函数,它们与途 径有关,而热力学能是状态函数,与途径无 (1)定义: 关。 当产物与反应物温度相同且化学反应时 只作膨胀功的条件下,化学反应过程中体系 Q=50KJ =30KJ 吸收或放出的热量称为反应热。 UII "Q=-40KJ) W=-60KJ 4
4 体系内部一切能量的总和: a.分子或原子的位能、振动能、转动能、 平动能、电子的动能以及核能等。 (5)热力学能U(内能) [thermodynamic energy (internal energy)] 第 3章化学反应概述 b.绝对值无法测量或计算,只能计算ΔU。 c.U是体系的状态函数。 d.理想气体的U只是温度的函数,恒温过 程△U=0。 e.具有加和性。 3.2.2热力学第一定律 • 数学表达式:ΔU = Q-W = Q - pΔV - W′ • 研究内容:体系变化过程中热力学能、功、 第 3章化学反应概述 研究内容:体系变化过程中热力学能、功、 热的转换方式。 • 实质:能量守恒和转化定律。 能量的总量是守恒的,不会凭空产生,也不会凭空 消失,只可能从一种形式转化为另一种形式。 • 在孤立体系中能量的总值恒定不变。 例:(1)某过程中,体系从环境吸收热量50kJ, 对环境做功30kJ。求过程中体系热力学能的改 变量ΔU和环境热力学能的改变量ΔU’。 解:由热力学第一定律的数学表达式可知 Q=+50kJ,W=+30kJ 第 3章化学反应概述 ∴ ΔU体系=Q-W =50-30=20(kJ) 若将环境当做体系来考虑, 则有Q’= 50kJ,W”= 30kJ, 故环境热力学能改变量ΔU’=Q’-W” ∴ΔU’环境= 50-(30)= 20(kJ) (2)如果开始时,体系先放热40kJ,环境 对体系做功60kJ,求体系的热力学能的改 变量ΔU以及终态的热力学能U 。 解: Q =-40kJ W = -60kJ 第 3章化学反应概述 解: Q = 40kJ,W = 60kJ ΔU体系= Q -W =20kJ ∴ UII= UI+20(kJ) 讨论: 对于体系的始态UI 和终态(UI +20), 虽然变化途径不同(Q、W不同),但ΔU却 相同。说明Q、W是非状态函数,它们与途 径有关,而热力学能是状态函数,与途径无 第 3章化学反应概述 关。 3.2.3 化学反应的热效应 1.化学反应热 (1)定义: 当产物与反应物 度相 化学反应时 第 3章化学反应概述 当产物与反应物温度相同且化学反应时 只作膨胀功的条件下,化学反应过程中体系 吸收或放出的热量称为反应热

(2)化学反应热的类型: ⅱ恒压反应热: 等压条件下,p△V=△(N) △U=Q-p△V=Q-△(W) ⅰ恒容反应热: Q=△U+p△V=△U+△(W) △U=Q-pAV: =(U2-U1)+(p2V2p1V1) 因为 △V=0: 定义一个新的热力学函数—烙H(enthalpy) 所以 △Uw=Q H=U+p 第 3 Q。=-H=△H。 Q,具有状态函数的性质一恒容条件下的 盖斯定律。 Q,具有状态函数的性质一恒压条件下的盖斯定律。 2.焙 H=U pV (3)恒容反应热与恒压反应热的关系(p58) H是状态函数,称为热焓,简称焓。具有加和性质。 1.Qp=△Hp,Qv-△Uv,-U+pY *注意 Qp-Qv=ap-AUv=△UptA(p)-△Uv=△(p) ·理想气体的烙H只是温度的函数,△T=0则△H=0。 2.讨论: *对不含气体的反应:△(p)很小,Qp-Qv 理短气体的熟力学 ·△H的具体数值与化学反应方程式的具体表达形 对含气体的反应: 能只是温度的通数 式有关,所以焓变要与具体的反应式同时出现。 pV=nRT,△(p门=△hRT)-RT△n, △Up-△ △n为反应前后气体摩尔数的变化 在书写反应式时不仅要表达出各反应物的计量关 系,还要表达出各个物质的物态,即气、固、液 即Qp-Qv+△nRT-Qv+(En-2nE)RT 态。 △H-AU+(En-2n度)RT 化学反 前提:理想气体,恒湿,不作非体积功 搅拌器3引燃线1温度计 例:求苯的燃烧反应的焓变 15 弹式量热计 绝热外套 C。H,0+20,(8)=6C0,(8)+3H,0W 钢制容器 解:根据氧弹量热计中苯的燃烧放热为3264kJ.moll得 第3章 钢弹 第37 水 Ar281=-3264×10+6-7x8314×239815 样品盘 =-32.7×102kJ-mo J
5 (2)化学反应热的类型: ⅰ 恒容反应热: ΔU=Q-pΔV; 因为 ΔV=0 第 3章化学反应概述 因为 ΔV=0; 所以 ΔUV=QV QV具有状态函数的性质——恒容条件下的 盖斯定律。 ⅱ 恒压反应热: 等压条件下, pΔV = Δ(pV) ΔU = Q - pΔV = Q -Δ(pV) Q = ΔU + pΔV = ΔU +Δ(pV) = (U2-U1)+(p2V2-p1V1) 焓 第 3章化学反应概述 定义一个新的热力学函数——焓H (enthalpy) H = U + pV Qp = H2-H1 = Hp Qp 具有状态函数的性质——恒压条件下的盖斯定律。 H 是状态函数,称为热焓,简称焓。具有加和性质。 *注意 • 理想气体的焓H只是温度的函数, T=0则H=0。 • H的具体数值与化学反应方程式的具体表达形 2. 焓 H = U + pV 第 3章化学反应概述 具 式具 式有关,所以焓变要与具体的反应式同时出现。 • 在书写反应式时不仅要表达出各反应物的计量关 系,还要表达出各个物质的物态,即气、固、液 态。 (3)恒容反应热与恒压反应热的关系(p58) 1.Qp=△Hp, Qv=△Uv, H=U+pV Qp-Qv=△Hp-△Uv= △Up+△(pV)-△Uv = △(pV) 2.讨论: *对不含气体的反应:△(pV)很小,Qp=Qv **对含气体的反应: 理想气体的热力学 能只是温度的函数, 第 3章化学反应概述 pV=nRT, △(pV)=△(nRT)=RT △n, △n为反应前后气体摩尔数的变化 即Qp=Qv+△nRT=Qv+(∑n产-∑n反)RT 能只是温度的函数, △Up=△Uv 前提:理想气体,恒温,不作非体积功 △H=△U+(∑n产-∑n反)RT 弹 式 第 3章化学反应概述 量热计 例:求苯的燃烧反应的焓变 ( ) 6 ( ) 3H O( ) 2 15 C H ( ) 6 6 2 2 2 l O g CO g l 第 3章化学反应概述 2 3 2 1 15 (298.15) 3264 10 (6 ) 8.314 298.15 2 32.7 10 rH kJ mol 解:根据氧弹量热计中苯的燃烧放热为3264kJ.mol-1得

4.化学反应热的计算 (1)盖斯定律(Hess'Law) 计算反应热的几种方法: 1.盖斯定律一利用状态函数的性质: 1840 Germain Henri Hess (1802-1850) 2.生成焓法一热力学函数标准摩尔生成 "the heat evolved or absorbed in a chemical 焓的导出(定义一个起点)。 process is the same whether the process takes place in one or in several steps" ·在等容或等压、不做非体积功的条件下,化学反应 化字反 的反应热只取决于反应的始态和终态,与反应的具 体途径无关。 (1)盖斯定律 应用 讨论 ·适用于等容、等压过程。 ·H和U的绝对值无法测得,但△=Q。, △U=Qy,可通过实验测得。 一个化学反应若能分解为几步来完成,总反应 的焓变△H等于各分步反应的焓变△H之和。 第3 。 盖斯定律表达式:(在等压或等容条件下) Q,Qy具有状态函数的性质,只取决于体 系的始态和终态,与途径无关。 △H=∑△,H 又 盖斯定律应用举例2 (2)生成焓法 Hg1am)+子Og1atm) 标准摩尔生成焓 H2(g)+C(graphite)+ 摩尔生成焓的定 0 102(g 1mo1某化合物时反应的 H=-M 摩尔生成烙。 Enthalpy of formation Ho(g 标准摩尔生成焓: 态下该化合物的生成焓 △H=-108.6kJ 的标准摩尔生成焓。简 The25℃ The c 记作 △rHn°,单 HCHO ( 6
6 4.化学反应热的计算 计算反应热的几种方法: 1. 盖斯定律——利用状态函数的性质; 第 3章化学反应概述 2. 生成焓法——热力学函数标准摩尔生成 焓的导出(定义一个起点) 。 (1)盖斯定律(Hess’ Law) 1840 Germain Henri Hess (1802 - 1850) 第 3章化学反应概述 • "the heat evolved or absorbed in a chemical process is the same whether the process takes place in one or in several steps” • 在等容或等压、不做非体积功的条件下,化学反应 的反应热只取决于反应的始态和终态,与反应的具 体途径无关。 (1)盖斯定律——应用 第 3章化学反应概述 一个化学反应若能分解为几步来完成,总反应 的焓变ΔrH 等于各分步反应的焓变ΔrHi之和。 盖斯定律表达式:(在等压或等容条件下) Δr H = ∑ΔrHi 讨论 • 适用于等容、等压过程。 • H和U的绝对值无法测得,但ΔH= Q , 第 3章化学反应概述 • H和U的绝对值无法测得,但ΔH Qp, ΔU= QV,可通过实验测得。 • Qp,QV 具有状态函数的性质,只取决于体 系的始态和终态,与途径无关。 盖斯定律应用举例2 第 3章化学反应概述 (2)生成焓法 • 标准摩尔生成焓 摩尔生成焓的定义:由指定单质生成 1mol某化合物时反应的焓变,成为该化合物的 摩尔生成焓 第 3章化学反应概述 。 标准摩尔生成焓:在一定温度和标准状 态下该化合物的生成焓称为该物质在此条件下 的标准摩尔生成焓。简称为标准摩尔生成焓。 记作 Δf Hm θ, 单位kJ·mol-1

标准摩尔生成焓 标准摩尔生成焓 例在P以及298.15K下, (1)C(石墨)+0(g)=C0(g) △,H(298.15K)=-393.5J·mo 标准状态 △H.cou(298.15K)=-393.5J-mol1 溶液中的物质A的浓度c=1nold血3 气相物质的分压等于101.3kPa (2)H(g)+O(g)=H,O() △,H(298.15)=-285.83/-mo △yHon(298.15K)=-285.83kJ.mol ·指定单质的标准摩尔生成格为零。 (298.15K 的标准摩尔生成焓可查表p366,附表3) 物质的标准生成焓是相对格值。 化学反所概 对于任意化学反应的标准摩尔焓变的计算 在101.3kPa,25℃(298.15K)条件下: 即 △H=? △,Hg=△,H-A,H 反应物aA+bB yY+Z生成物 △,H (终态)1 (终态)2 △,H9 A,H298.15K0=vAH88,298.15K0 同样数量和种类 第 的稳定态各单质 =2(v,△yH)生物-2(V,△yH)反陈物 (始态) 草 △,H9=△H+△Hg 化学反应概述 注意 恒压反应热计算举例1 0 联氨燃烧反应 >各种物质的聚集状态。 吸热反应,△H>0 >反应焓变的数值与化学 N,,()+0,g)-2®)+2组,0(1) 反应方程式的计量有关。热 arHo 50.6300 -285.83 >△H>0,吸热反应: △H在常温常压下一般将其 视为常数。 华 H 7
7 标准摩尔生成焓 标准状态 溶液中的物质A的浓度cA=1mol•dm-3 气相物质的分压等于101 3kP 第 3章化学反应概述 气相物质的分压等于101.3kPa • 指定单质的标准摩尔生成焓为零。(298.15K 的标准摩尔生成焓可查表p366,附表3) • 物质的标准生成焓是相对焓值。 例 在Pθ以及298.15K下, (1) C(石墨 ) + O2(g) = CO2(g) 1 (298.15 ) 393.5 rH K kJ mol (2) H (g) + ½ O (g)=H O(l) 1 H K kJ l (298 15 ) 285 83 2 1 , () (298.15 ) 393.5 f m CO g H K kJ mol 标准摩尔生成焓 第 3章化学反应概述 (2) H2(g) + ½ O2(g) = H2O(l) 1 (298.15 ) 285.83 rH K kJ mol 2 1 , () (298.15 ) 285.83 f mHOl H K kJ mol 在101.3kPa,25℃(298.15 K)条件下: 反应物 aA + bB = yY + zZ 生成物 H (终态)2 3 ? rH (终态)1 第 3章化学反应概述 同样数量和种类 的稳定态各单质 (始态) rH2 (终态)2 rH1 (终态)1 r rr HHH 213 r rr H HH 3 21 即 H K HB K (298 15 ) ( 298 15 ) 对于任意化学反应的标准摩尔焓变的计算 第 3章化学反应概述 (298.15 ) ( ,298.15 ) r Bf m B H K HB K ()() if m if m H H 生成物 反应物 各种物质的聚集状态。 反应焓变的数值与化学 反应方程式的计量有关。 ΔH >0 吸热反应 注意 热 H 吸热反应, ΔH >0 第 3章化学反应概述 ΔH >0,吸热反应; ΔH <0,放热反应。 正负号不可忽略!!! 在常温常压下一般将其 视为常数。 H 放热反应, ΔH <0 热 恒压反应热计算举例I N2H4(l) + O2(g)=N2(g)+2H2O(l) △fHm o 50.63 0 0 -285.83 联氨燃烧反应 第 3章化学反应概述 △Hm o(298.15K)=(-285.83×2+0)-(0+50.63) = -622.29KJ/mol = -20.7KJ/g

C0,△H·=-283.0kJmo1-1 n-C6H14),△L°=-4141.52kJmo1-1 食物的热量 n-CgH18),4H°=-5450.76kJmo1-1 Approxiinate Composition (%by mass Fuel Value gca 05 品 蟹 化学反概述 Fuels Fuels U.S.:1.0 X 105 kJ of fuel per day. Fuel value energy released when 1 g of substance is burned. Hydrogen has great potential as a fuel with a fuel value Ful Values and Compositons of Some Camen Fuels of 142 kJ/g. Approximelo日omontal corposnion HO网a阳Kg塑 2 0250 0006 3草 化学反应概述 自发过程举例一放热 3.2.4化学反应进行的方向 甲烷燃烧 1.自发过程 铁 ·给定条件下,不需外加能量即能自动进行。 锈 ·限度一达到平衡状态。 CHa(g)+20:(g)=CO:(g)+2H:0(g) 2Fe(s)+O:(g)=Fe2Os(s) 第·逆过程一非自发过程一没有外加能量的 第3章 △H=-8023kmo △H=-824J-mo 情况下不能自动进行。 化学反应概 放热过程 8
8 CO, ΔcHm θ = - 283.0 kJ·mol-1 n-C6H14(l), ΔcHm θ = – 4141.52 kJ·mol-1 n-C8H18(l), ΔcHm θ = – 5450.76 kJ·mol-1 第 3章化学反应概述 食物的热量 第 3章化学反应概述 Fuels U.S.: 1.0 × 106 kJ of fuel per day. 第 3章化学反应概述 Fuels Fuel value = energy released when 1 g of substance is burned. Hydrogen has great potential as a fuel with a fuel value of 142 kJ/g. 第 3章化学反应概述 3.2.4 化学反应进行的方向 1.自发过程 • 给定条件下,不需外加能量即能自动进行。 第 3章化学反应概述 • 限度——达到平衡状态。 • 逆过程——非自发过程——没有外加能量的 情况下不能自动进行。 自发过程举例—放热 第 3章化学反应概述 放热过程

自发过程举例一吸热 这些现象是吸热过程,但也自发进行 自发过程的共同特征 )只能单向自发进行而不可能自发逆向进行。 b)要使其逆向进行,必须借助外力。 c)可能用来作功。 d)有一定的进行限度。 豪化钾等盐典凉解 许多现象说明,放热过程是常见的自发过程, 但并不唯一。 化学反概送 可逆途径 ·体系经历一个过程从某一始态变到某一 可逆途径 终态后,若能经另一过程使体系和环 ·是一种理想方式,其中间步骤都是可以逆 境都完全复原至始态,则原来的变化 转的 途径称为可逆途径:否则,若用任何方 ·在同样的始终态之间可以有许多不同的途 法都不可能使体系和环境完全复原,则 径,则其中的可逆方式下体系所做的功为 是不可逆途径。 最大 化学反应概 eg准静态膨胀或压缩过程: 液体在其沸点时的蒸发,周体在其熔点时的熔化 一步膨胀: W-F△L=PA△L=PAV 无限多步膨胀: P外=P铁-dP =0.5(20.0-10.0)=5.0am-1 二步膨胀: 形=pdW=f(Ps-pdr 3=0.7513.3-10.0)+0.520.0-13.3) =5.83atm-l -收par- 三步膨胀: 第3章 n吃=r哈 V 始态:1atm,10.01 f2=0.812.5-10.0+0.606.7-12.5)+0.520.0-16.7) 终态:0.5atm,20.01 =6.17am-1 化学反应概 =6.93atm-l 9
9 自发过程举例—吸热 这些现象是吸热过程,但也自发进行 第 3章化学反应概述 许多现象说明,放热过程是常见的自发过程, 但并不唯一。 自发过程的共同特征 a) 只能单向自发进行而不可能自发逆向进行。 b) 要使其逆向进行,必须借助外力。 ) 可能用来作功 第 3章化学反应概述 c) 可能用来作功。 d) 有一定的进行限度。 可逆途径 • 体系经历一个过程从某一始态变到某一 终态后,若能经另一过程使体系和环 境都完全复原至始态 则原来的变化 第 3章化学反应概述 境都完全复原至始态,则原来的变化 途径称为可逆途径;否则,若用任何方 法都不可能使体系和环境完全复原,则 是不可逆途径。 可逆途径 是一种理想方式,其中间步骤都是可以逆 转的 第 3章化学反应概述 在同样的始终态之间可以有许多不同的途 径,则其中的可逆方式下体系所做的功为 最大 e.g. 准静态膨胀或压缩过程; 液体在其沸点时的蒸发,固体在其熔点时的熔化 一步膨胀: 1 0.5(20.0 10.0) 5.0 W F L PA L P V atm l 外 始态: 1atm, 10.0l 终态:0.5atm, 20.0l 二步膨胀: 2 0.75(13.3 10.0) 0.5(20.0 13.3) 5.83a l W tm 三步膨胀: 2 0.8(12.5 10.0) 0.6(16.7 12.5) 0.5(20.0 16.7) 6.17a W tm l 无限多步膨胀: P外 P系统 dP 2 2 ( ) V V W P dV P dp dV 外 系统 第 3章化学反应概述 1 1 2 2 1 1 2 2 1 1 ( ) ln ln 6.93 V V V V V r V P dV P dp dV nRT P dV dV V V V nRT PV V V atm W l 外 系统 系统

膨胀功和压缩功比较 2.热力学熵(S)及其物理意义 (1)熵的微观本质 ·熵的概念:混乱度、微观状态数: ·熵的性质:具有加和性: 步骤数 膨胀功(am.压缩功(atm.) 结论 ·联系宏观与微观的热力学函数: 一步 5.00 10.00 S=kIno 章 不可逆 三步 6.17 7.84 Boltzmann?常数 无限多步 6.93 6.93 可逆 化学反概述 k=1.38×1023J·K-1 熵增过程 8 固体 液体 (a)熔化:S> b)蒸发:S气>S Taluene (C.H.CH 部款 三种熵增过程 溶质 容剂 ()溶解宫夜>(容质+容剂) 化学反概 孤立体系总是从热力学根率小的宏观态(非平衡态) 向热力学率大的宏观态(平衡态)过渡。 熵和分子的结构 Uo 1.Temperature Change:273K 295K 298K Cu:S,(J/mol-K)31.0 32.9 33.1 29 程2% Solid Liquid Gas 21374 5H.7 Na:s°,d/mol351.4 153.6 H,0:S°,d/mol9· 69.9 188.7 41 440 389 化学反应概 10
10 膨胀功和压缩功比较 第 3章化学反应概述 步骤数 膨胀功(atm.l) 压缩功(atm.l) 结论 一步 5.00 10.00 不可逆 三步 6.17 7.84 无限多步 6.93 6.93 可逆 2. 热力学熵(S)及其物理意义 (1)熵的微观本质 • 熵的概念:混乱度、微观状态数; • 熵的性质:具有加和性; 第 3章化学反应概述 • 联系宏观与微观的热力学函数: S k ln Boltzmann常数 k=1.38×1023J • K -1 第 3章化学反应概述 熵增过程 第 3章化学反应概述 孤立体系总是从热力学概率小的宏观态(非平衡态) 向热力学概率大的宏观态(平衡态)过渡。 熵和分子的结构 第 3章化学反应概述 Sθ 1. Temperature Change: 273K 295K 298K Cu: S°, (J/mol•K) 31.0 32.9 33.1 第 3章化学反应概述 2. Phase Change: Solid Liquid Gas Na : S°, (J/mol•K) 51.4 - 153.6 H2O : S°, (J/mol•K) - 69.9 188.7