
系统发生自发变化有两种驱动力 通过放热使系统趋向于最低能量状态 系统趋向于最大混乱度

★熵与微观粒子状态数关系 1878年,L.Boltzman提出 了熵与微观状态数的关系 S=kIn2 S-熵 玻耳兹曼 2-微观状态数 (Boltzmann L,1844-1906) 奥地利物理学家 k--Boltzman常量 R 8.314J .mol -1.K-1 k= NA 6.022×1023m0l -1 1.3806×10-23J.K1
★ 熵与微观粒子状态数关系 1878年,L.Boltzman提出 了熵与微观状态数的关系 S = klnΩ S---熵 Ω---微观状态数 k--- Boltzman常量 -23 -1 23 -1 -1 -1 A 1.3806 10 J K 6.022 10 mol 8.314J mol K N R k 玻耳兹曼 (Boltzmann L,1844-1906) 奥地利物理学家

热力学第三定律 The third law of thermodynamics 纯物质完整有序晶体在0K时的熵值为零 S(完整晶体,0K)=0 (a)0K (b)稍大于0K 通过s(0K 值和其他有关热力学数据,可以算得物 质在温度高于0K时的绝对熵S(T)
纯物质完整有序晶体在0K时的熵值为零 S0 (完整晶体,0 K) = 0 通过 值和其他有关热力学数据,可以算得物 质在温度高于0 K时的绝对熵 。 0K) θ S ( ) θ S (T

标准摩尔熵的一些规律 物质的熵值随温度升高而增大。例如,CS,(①)在 161K和298K时的S8值分别为103J小mo1K1 和150J·mo1.K-1。 2. 同一物质在气态的熵值总是大于液态的熵值,而后 者又大于固态的熵值。 △S>0 4S>0 △S<0 AS<0 3.气态多原子分子的S值比单原子分子大,例如: N2(g) NO(g) NO2(g) 153 210 240
2. 同一物质在气态的熵值总是大于液态的熵值,而后 者又大于固态的熵值。 1. 物质的熵值随温度升高而增大。例如, CS2(l)在 161K 和 298 K时的 值分别为 103 J·mol -1·K-1 和150 J · mol -1·K-1 。 θ S m N2(g) NO(g) NO2(g) 153 210 240 3. 气态多原子分子的 值比单原子分子大,例如: θ S m
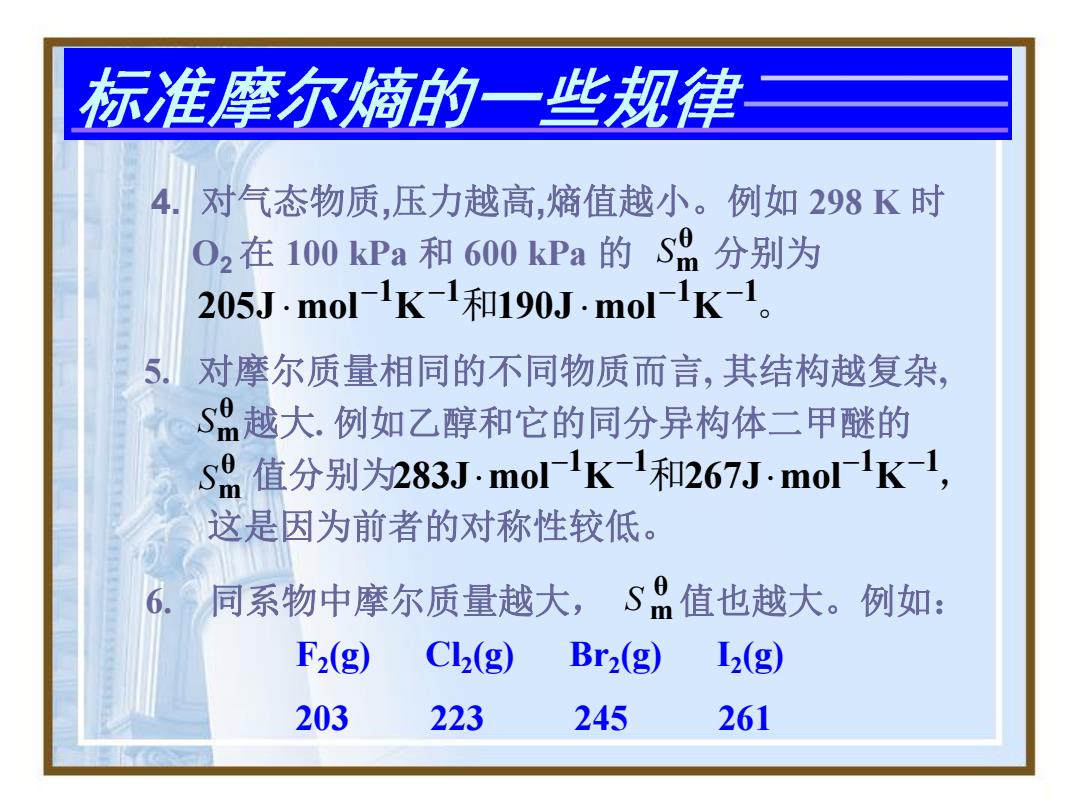
标准摩尔熵的一些规律 4.对气态物质,压力越高,熵值越小。例如298K时 O2在100kPa和600kPa的S8分别为 205Jmol-1K-1和190J·mol-1K-1。 对摩尔质量相同的不同物质而言,其结构越复杂, S越大.例如乙醇和它的同分异构体二甲醚的 sA值分别为283J·molK-1和267J-mol-K1, 这是因为前者的对称性较低 同系物中摩尔质量越大,S 值也越大。例如: F2(g) Cl2(g) Br2(g) 12(g) 203 223 245 261
5. 对摩尔质量相同的不同物质而言, 其结构越复杂, 越大. 例如乙醇和它的同分异构体二甲醚的 值分别为 这是因为前者的对称性较低。 θ Sm θ Sm 283Jmol1K 1和267Jmol1K 1 , 6. 同系物中摩尔质量越大, 值也越大。例如: F2(g) Cl2(g) Br2(g) I2(g) 203 223 245 261 θ S m 4. 对气态物质,压力越高,熵值越小。例如 298 K 时 O2 在 100 kPa 和 600 kPa 的 分别为 205J mol1K 1和190J mol1K 1 。 θ Sm

化学和物理变化过程的熵变 熵变(△S)与焓变相对应: AS=∑yS(终态物质)-∑S(始态态物 ) AS=∑yS(态物质)-∑ySH(始态态物 热力学第二定律 The second law of thermodynamics 在任何自发过程中,体系和环 △S总=(△S体系+△S环境 )> 自发变化 境的熵变化的总和是增加的 AS点>0 AS总<0 非自发变化 克劳修斯表述: 热从低温物体传给高温 AS总 =0 平衡状态 物体,而不产生其他变化是不可能的。 开尔文表述:从一个热源吸热,使之完全转 化为功,而不产生其他变化是不可能的
化学和物理变化过程的熵变 熵变 与焓变相对应: 平衡状态 非自发变化 自发变化 总 总 总 总 体系 环境 0 0 0 0 S S S S S S 在任何自发过程中,体系和环 境的熵变化的总和是增加的 ( ) ( ) ( ) ( ) θ i m θ j m θ m j i 终态物质 始态态物 终态物质 始态态物 S v S v S S v S v S (S) 克劳修斯表述:热从低温物体传给高温 物体,而不产生其他变化是不可能的。 开尔文表述:从一个热源吸热,使之完全转 化为功,而不产生其他变化是不可能的

Ques 已知H2,N,和NH3在298K的 标准熵分别为130.6J·mo1K1,191.5 Jmo1K-1和192.3J·mo1.K-1,试计 算反应3H2(g)+N2(g)→2NH3(g) 的标准摩尔熵。 AS=2×SA(NH3)-[3×Sa(H2)+1×Sm(N2】 =2X192.3Jmo1.K-1 3×130.6J。·mo1.K-1-1×191.5J·mo1.K-1 =-198.3Jmo1.K-1
已知 H2,N2和 NH3在 298 K 的 标准熵分别为 130.6 J · mol -1·K-1 , 191.5 J·mol -1·K-1和 192.3 J · mol -1·K-1,试计 算反应 3H2(g) + N2(g) 2 NH3(g) 的标准摩尔熵。 Solution = 2×192.3 J·mol -1·K-1 -3×130.6 J · mol -1·K-1-1×191.5 J · mol -1·K-1 = -198.3 J∙mol -1·K-1 Question ( ) [ ( ) ( )] 2 θ 2 m θ 3 m θ m θ Sm 2 S NH 3 S H 1 S N

自由能— 反应自发性的最终判据 Free energy-the determined criterion for 1 the spontaneous process 如果综合两种反应自发性驱动力,就会得到 △G=△H-T△S(吉布斯-亥姆霍兹公式) 定义 G=H-TS Gibbsi函数(Gibbs free energy) G是状态函数,与焓一样,人们只能测得或 算得自由能变(△©,而无法得到G本身。 (Gibbs J,1839-1903)
如果综合两种反应自发性驱动力,就会得到 △G = △H - T △S (吉布斯-亥姆霍兹 公式) 定义 G = H - TS G Gibbs函数(Gibbs free energy) G是状态函数,与焓一样,人们只能测得或 算得自由能变(△G),而无法得到G本身。 自由能——反应自发性的最终判据 Free energy-the determined criterion for the spontaneous process (Gibbs J ,1839-1903)

应用Gibbs函数〈变→ 可以判据化学反应进行的方向 在定温定压下,任何自发变化总是体系的Gbbs 函数减小。 △G0 反应是非自发的,能逆向进行 △G=0 反应处于平衡状态 △G代表了化学反应的总驱动力,它就是化学家长 期以来所寻找的、明确判断过程自发性的那个物理量!
在定温定压下,任何自发变化总是体系的Gibbs 函数减小。 △G 0 反应是非自发的,能逆向进行 △G = 0 反应处于平衡状态 △G代表了化学反应的总驱动力,它就是化学家长 期以来所寻找的、明确判断过程自发性的那个物理量!

标准摩尔生成bbs焓 The standard free energy of molar formation 在温度TK下,由参考状态的单质生成1mol物 质B的反应的标准摩尔Gibbs函数变,称为物质B的标 准摩尔生成Gibbsi函数。 △rGA(B,相态,T) △G(参考态单质,T)=0 化学反应的标准摩尔Gibbsi函数为 △GHn≈△rHl-T△SA
θ r m θ r m θ rGm H T S 0 B θ f m θ f m G T G T , , 参考态单质 ,相态 化学反应的标准摩尔Gibbs函数为 在温度T K下,由参考状态的单质生成1 mol物 质B的反应的标准摩尔Gibbs函数变,称为物质B的标 准摩尔生成Gibbs函数