
HEAT TRANSFER CHAPTER 8 Internal flow Heat Transfer #1 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 1 HEAT TRANSFER CHAPTER 8 Internal flow
Internal Flow Heat Transfer Where we've been ..... Introduction to internal flow,boundary layer growth,entry effects Inviscid flow region Boundary layer region u(r.x) Hydrodynamic entrance region Fully developed regior xtd. Where we're going: Developing heat transfer coefficient relationships and correlations for internal flow Heat Transfer #2 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 2 Internal Flow Heat Transfer Where we’ve been …… • Introduction to internal flow, boundary layer growth, entry effects Where we’re going: • Developing heat transfer coefficient relationships and correlations for internal flow ro

Internal Flow Heat Transfer KEY POINTS THIS LECTURE 。 Energy balance for internal flow in a tube Temperature and heat transfer relations for two cases: Constant surface heat flux Constant surface temperature Heat Transfer #3 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 3 Internal Flow Heat Transfer KEY POINTS THIS LECTURE • Energy balance for internal flow in a tube • Temperature and heat transfer relations for two cases: – Constant surface heat flux – Constant surface temperature

Basic concepts-thermal considerations .1.The mean temperature Inviscid flow region Boundary layer region (r,x) Hydrodynamic entrance region Fully developed regior Xid.h For the internal energy E,=∫puc,TdA and E,三imC,Tm So puc,7TdA.∫puc,TA. T.= mcy pumAcy For incompressible flow in a circular tube, 2 uTrdr Heat Transfer #4 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 4 Basic concepts—thermal considerations • 1. The mean temperature • For the internal energy • So • For incompressible flow in a circular tube, ro Ac t u vTdAc E c t vTm E m c and m c v A v c v A v c m u A c uc TdA mc uc TdA T c c 0 0 2 0 2 r m m uTrdr u r T

Basic concepts-thermal considerations 2.Newton's law of cooling qs=h(T,-Tm力 Not constant! Here,the mean T plays the same role as the free stream T for external flows. 3.Fully developed conditions because of heat transfer,T(r)is continuously changing with x. can fully developed conditions be reached?? For thermally fully developed a T,(x)-T(r,x) =0 x T(x)-T (x) Although the temperature profile T(r)changes with x,the relative shape of the profile no longer changes. Heat Transfer #5 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 5 Basic concepts—thermal considerations • 2. Newton’s law of cooling • Here, the mean T plays the same role as the free stream for external flows. • 3. Fully developed conditions because of heat transfer, T(r) is continuously changing with x. can fully developed conditions be reached?? • For thermally fully developed • Although the temperature profile T(r) changes with x, the relative shape of the profile no longer changes. ( ) qs h Ts Tm T Not constant! 0 ( ) ( ) ( ) ( , ) , m fd t s s T x T x T x T r x x

Basic concepts-thermal considerations o In the thermally fully developed flow of a fluid with constant properties,the local convection coefficient is a constant,independent of x. h≠f(x) For the special case of uniform surface heat flux ot Axial T dT Independent of gradient Ox fd,t dx fd.t radial location q"cons tant For the case of constant surface temperature Depends on the ot (Ts -T)dTmn radial coordinate 8x\fd. (Ts-Tm)dx T,cons tant Heat Transfer #6 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 6 Basic concepts—thermal considerations • In the thermally fully developed flow of a fluid with constant properties, the local convection coefficient is a constant, independent of x. • For the special case of uniform surface heat flux • For the case of constant surface temperature h f (x) fd t m fd t dx dT x T , , q cons t s tan Axial T gradient Independent of radial location fd t m s m s fd t dx dT T T T T x T , , ( ) ( ) T cons t s tan Depends on the radial coordinate

Example:Velocity and temperature profiles for laminar flow in a tube of radius r=10mm have the form )=0.l-(1] T(r)=344.8+75.0r/-18.8r/) with units of m/s and K,respectively.Determine the corresponding value of the mean (or bulk) temperature,,at thisaxial position KNOWN:Velocity and temperature profles for laminar flow in a tube of radius10mm FIND:Mean(r bulk)temperature,T at this axial position. SCHEMATIC: ,T0 Fluid ASSUMPTIONS:(1)Laminar incompressible flow,(2Constant propertes. Heat Transfer #7 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 7 Example: Velocity and temperature profiles for laminar flow in a tube of radius have the form with units of m/s and K, respectively. Determine the corresponding value of the mean (or bulk) temperature, , at this axial position. ro 10mm Tm 2 4 2 ( ) 344.8 75.0 / 18.8 / ( ) 0.11 / o o o T r r r r r u r r r
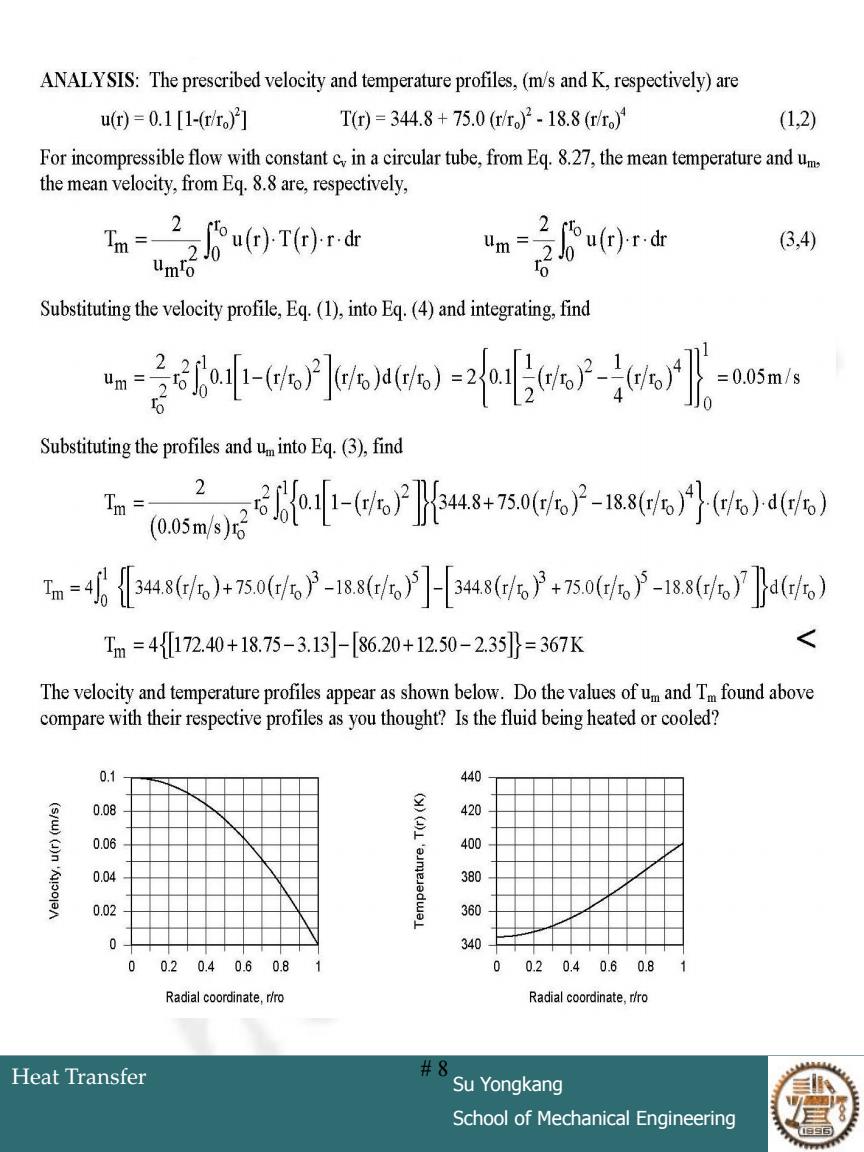
ANALYSIS:The prescribed velocity and temperature profiles,(m/s and K,respectively)are ut=0.1[1-r] Tr)=344.8+75.0(rr)2-18.8(rr)4 (1,2) For incompressible flow with constant c in a circular tube,from Eq.8.27,the mean temperature and um the mean velocity,from Eq.8.8 are,respectively, aa (3,4) Substituting the velocity profile,Eq.(1),into Eq.(4)and integrating,find i)am Substituting the profiles and uinto Eq.(3),find h-oeiseaseus-iae-oos)oe n=4348t,)+75otP-18to]-3486户+750t6户-1s8t。7a(6o) Tm=4172.40+18.75-3.13]-[86.20+12.50-2.35}=367K < The velocity and temperature profiles appear as shown below.Do the values of um and Tm found above compare with their respective profiles as you thought?Is the fluid being heated or cooled? 0.1 440 0.08 420 0.06 400 0.04 380 0.02 360 340 0 0.20.40.60.8 1 0 0.20.40.60.81 Radial coordinate,r/ro Radial coordinate,r/ro Heat Transfer #8 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 8

Review:Energy Balance Analysis Eim.adv=i Cp Tmx in.dv Bout.ady Eo,ady=mi cp Tm.x+ds Econ =gcomP.dx=comdx X x+dx Energy Balance Change in energy in the control volume energy input-work out energy in by advection energy carried out by advection(flow) or 0=qoom P.dx ri cp Tm.x-li cp Tm.xtd 0=qcom·P.dk -i cp dTm dIn.=P=,-Tn) dx mcp mcp Two Special Cases: 1.Constant surface heat flux 2.Constant surface temperature Heat Transfer #9 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 9 Review: Energy Balance Analysis x x + dx Ein,adv Eout,adv Econvection Energy Balance Change in energy in the control volume = energy input – work out + energy in by advection – energy carried out by advection (flow) or Two Special Cases: 1. Constant surface heat flux 2. Constant surface temperature E q P dx q dx E m c T E m c T conv conv conv out adv p m x dx in adv p m x , , , , 0 0 , , s m p p m conv conv p m conv p m x p m x dx h T T m c P m c q P dx dT q P dx m c dT q P dx m c T m c T

Case 1:Constant Surface Heat Flux ·Example application Electrical heater element around a pipe Recognize that: qg≠f(x) From the energy balance equation 7(田=Tn+gPx ·ifq”is constant Entrance region Fully developed region T.() If g"is a known function of x instead,must T.(x) integrate the above to obtain Tm.x g=constant Heat Transfer #10 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 10 Case 1: Constant Surface Heat Flux • Example application – Electrical heater element around a pipe • Recognize that: • From the energy balance equation • if q ” is constant If q ” is a known function of x instead, must integrate the above to obtain Tm,x q f (x) s ( ) Tm,i x m c q P T x p s m