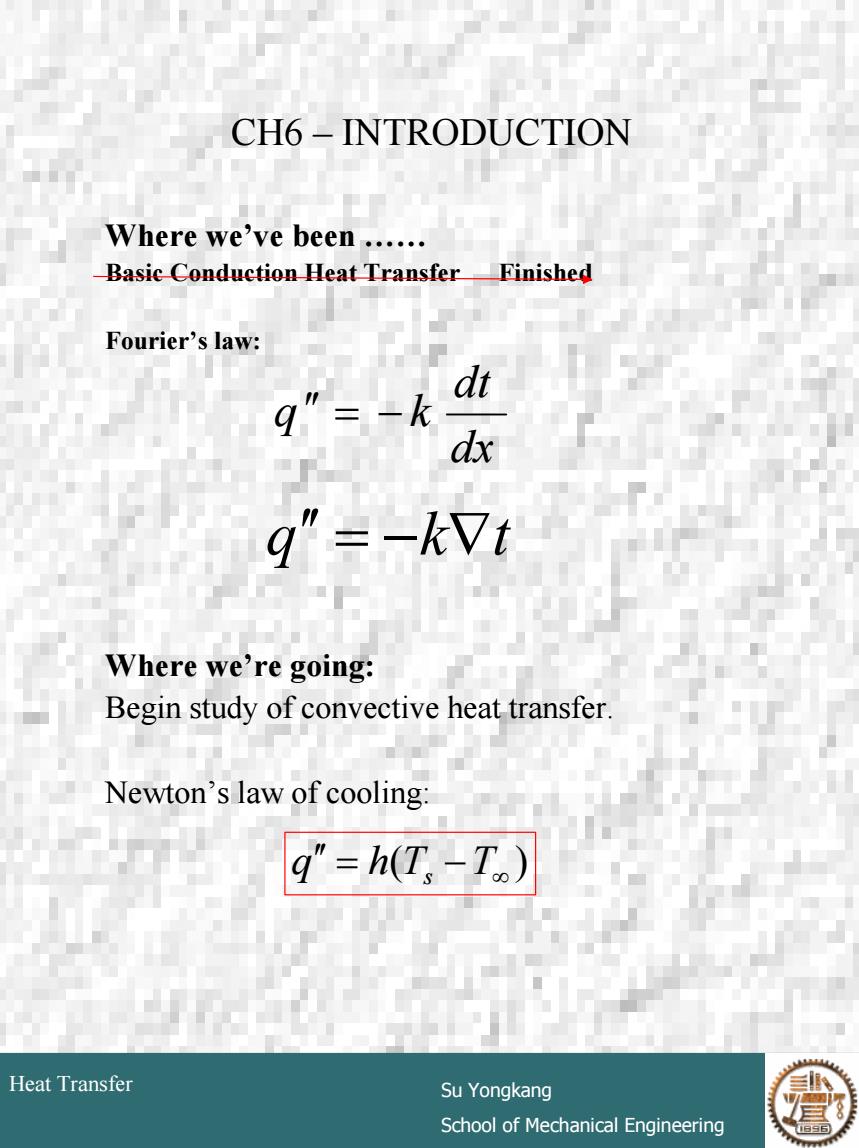
CH6-INTRODUCTION Where we've been...... Basic Conduction Heat Transfer Finished Fourier's law: q"=-k dt dx g"=-kVt Where we're going: Begin study of convective heat transfer. Newton's law of cooling: q"=h(T,-T) Heat Transfer Su Yongkang School of Mechanical Engineering
# 4 Heat Transfer Su Yongkang School of Mechanical Engineering CH6 – INTRODUCTION Where we’ve been …… Basic Conduction Heat Transfer Finished Fourier’s law: Where we’re going: Begin study of convective heat transfer. Newton’s law of cooling: dx dt q ′′ = − k q ′′ = −k∇t ( ) = − ∞ q ′′ h Ts T

Convective transfer problem A FAMILY CIRCUS 2-6 D2o02 BIKeane,nt Dt tyKng Frmn世Srd hEAM FIRCUS. 蒸 "I forget.Does holding the door open let the cold air in,or the warm out?" Heat Transfer Su Yongkang School of Mechanical Engineering
# 5 Heat Transfer Su Yongkang School of Mechanical Engineering Convective transfer problem

CH6 INTRODUCTION KEY POINTS THIS CHAPTER What are the key variables when analyzing convection heat transfer? Review boundary layer concept and significance General idea of relationship between velocity and thermal profiles in a boundary layer. Effect of laminar versus turbulent flow on heat transfer potential Boundary layer similarity This chapter will be taught in two lectures: the first includes text book sections 6.1 to 6.4 the other includes text book sections 6.5 to 6.10 Heat Transfer Su Yongkang School of Mechanical Engineering
# 6 Heat Transfer Su Yongkang School of Mechanical Engineering CH6 INTRODUCTION KEY POINTS THIS CHAPTER • What are the key variables when analyzing convection heat transfer? • Review boundary layer concept and significance • General idea of relationship between velocity and thermal profiles in a boundary layer. • Effect of laminar versus turbulent flow on heat transfer potential • Boundary layer similarity • This chapter will be taught in two lectures: the first includes text book sections §6.1 to 6.4 the other includes text book sections §6.5 to 6.10

Convection overview Consider a flat plate of length L,in air flow with velocity u and temperature To yA 1 1 Local heat flux is: where h is the local heat transfer coefficient q"=h(T,-T) Total heat transfer rate: 9=∫9d4,=(T,-T) hdA. q=hA,(Ts-T) 万= average heat transfer coefficient Determination of h'will rely on analytical as well as empirical data Heat Transfer Su Yongkang School of Mechanical Engineering
# 7 Heat Transfer Su Yongkang School of Mechanical Engineering Convection overview • Consider a flat plate of length L, in air flow with velocity u∞ and temperature T∞ • Local heat flux is: where h is the local heat transfer coefficient • Total heat transfer rate: ( ) = − ∞ q ′′ h Ts T ∫ ∞ ∫ = ′′ = − s As s s A s q q dA (T T ) hdA ( ) q = hAs Ts −T∞ average heat transfer coefficient h = Determination of ‘h’ will rely on analytical as well as empirical data

Convection overview(Cont'd) Same principal applies to any arbitrary shape,not just a flat plate dAs As:Ts Average convection heat transfer coefficient: or,for unit width: d So,we need to know how h varies with x,the distance from the leading edge...... What do you think key parameters that might influence h? Heat Transfer Su Yongkang School of Mechanical Engineering
# 8 Heat Transfer Su Yongkang School of Mechanical Engineering Convection overview (Cont’d) • Same principal applies to any arbitrary shape, not just a flat plate • Average convection heat transfer coefficient: So, we need to know how h varies with x, the distance from the leading edge…….. What do you think key parameters that might influence h? q ′′ dAs As Ts , or, for unit width: ∫ = As s s hdA A h 1 ∫ = L hdx L h 0 1

Key parameters Transfer potential:forced flow or free flow Phase change:boiling and condensation Flow conditions:laminar or turbulent flow Geometries:shape,size,position and roughness. Properties:density,viscosity,thermal conductivity,specific heat,and so on. Heat Transfer Su Yongkang School of Mechanical Engineering
# 9 Heat Transfer Su Yongkang School of Mechanical Engineering Key parameters • Transfer potential: forced flow or free flow • Phase change: boiling and condensation • Flow conditions: laminar or turbulent flow • Geometries: shape, size, position and roughness. • Properties: density, viscosity, thermal conductivity, specific heat, and so on
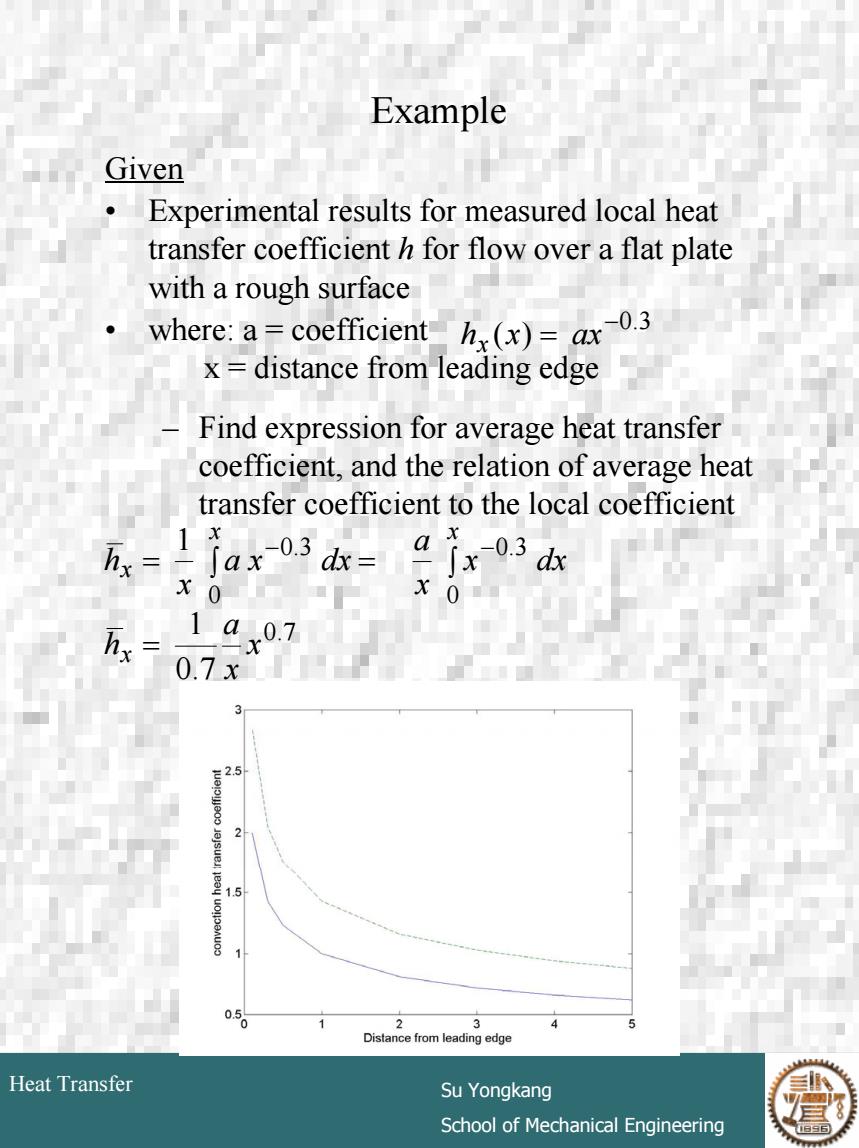
Example Given Experimental results for measured local heat transfer coefficient h for flow over a flat plate with a rough surface 0.3 where:a=coefficienth(x)=ax x=distance from leading edge Find expression for average heat transfer coefficient,and the relation of average heat transfer coefficient to the local coefficient 万x= I jax03ds=ajx3d X0 hx 1ax07 0.7x 2.5 1.5 050 2 Distance from leading edge Heat Transfer Su Yongkang School of Mechanical Engineering
# 10 Heat Transfer Su Yongkang School of Mechanical Engineering Example Given • Experimental results for measured local heat transfer coefficient h for flow over a flat plate with a rough surface • where: a = coefficient x = distance from leading edge – Find expression for average heat transfer coefficient, and the relation of average heat transfer coefficient to the local coefficient ( ) −0.3 h x = ax x 0.7 0 0.3 0 0.3 0.7 1 1 x x a h x dx x a a x dx x h x x x x = = ∫ = ∫ − −

The Convection Boundary Layers Velocity Boundary Layer Free stream 一6(x) Velocity boundary layer For fluid flow over a flat plate,which disturbs the fluid flow: -ASy→0: u=uo where u is velocity in x-direction Asy-→0: u=0 (no-slip condition) The boundary layer thickness is defined as the value at which: u(y)=0.99u。 - The boundary layer thickness 8 varies with x Shear Stress Bu ay Dynamic viscosity y=0 Local friction coefficient u 2 Heat Transfer Su Yongkang School of Mechanical Engineering
# 11 Heat Transfer Su Yongkang School of Mechanical Engineering The Convection Boundary Layers Velocity Boundary Layer • For fluid flow over a flat plate, which disturbs the fluid flow: – As y→∞: where u is velocity in x-direction – As y→0: (no-slip condition) – The boundary layer thickness is defined as the value at which: – The boundary layer thickness δ varies with x • Shear Stress • Local friction coefficient =0 ∂ ∂ = y s y u τ µ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ∞ 2 2 u C s f ρ τ = ∞ u u u = 0 = ∞ u( y) 0.99u Dynamic viscosity

The Convection Boundary Layers Thermal Boundary Layer Free stream 6,x) Thermal boundary layer 一T,≠To T. A hot or cold plate alters the temperature distribution in the air -Asy-→o:T(y)=T - Asy→0:T(y)=T, The thermal boundary layer thickness is defined as the value at which: T,-Tair(y)=0.99 Ts-Too The thermal boundary layer thickness,t also varies (increases)with x Heat Transfer Su Yongkang School of Mechanical Engineering
# 12 Heat Transfer Su Yongkang School of Mechanical Engineering The Convection Boundary Layers Thermal Boundary Layer • A hot or cold plate alters the temperature distribution in the air – As y→∞: – As y→0: – The thermal boundary layer thickness is defined as the value at which: – The thermal boundary layer thickness, δt also varies (increases) with x 0.99 ( ) = − ∞ − T T T T y s s air Ts ≠ T∞ = T∞ T( y) Ts T( y) =

The Convection Boundary Layers Thermal Boundary Layer (Cont'd) Free stream 6,) Thermal boundary layer 一T,≠T0 T Heat Flux 0 Heat flux analogous to shear stress in velocity boundary layer Heat flux proportional to the temperature gradient at the surface, AND since u(y=0)-0,energy transfer to/from fluid occurs by conduction only! wall at temperature fluid thermal gradient conductivity y=0 Since thermal boundary layer gets larger along x direction,the temperature gradient changes with x,and therefore Heat Transfer Su Yongkang School of Mechanical Engineering
# 13 Heat Transfer Su Yongkang School of Mechanical Engineering The Convection Boundary Layers Thermal Boundary Layer (Cont’d) Heat Flux • Heat flux analogous to shear stress in velocity boundary layer • Heat flux proportional to the temperature gradient at the surface, AND since u(y=0) =0, energy transfer to/from fluid occurs by conduction only! • Since thermal boundary layer gets larger along x direction, the temperature gradient changes with x, and therefore Ts ≠ T∞ fluid thermal conductivity wall temperature gradient ____________________ =0 ∂ ∂ ′′ = − y s f y T q k