
HEAT TRANSFER CHAPTER 8 Internal flow Heat Transfer #1 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 1 HEAT TRANSFER CHAPTER 8 Internal flow

Internal Flow Heat Transfer Where we've been ..... Introduction to internal flow,basic concepts, energy balance. Inviscid flow region Boundary layer region u(r.x) Hydrodynamic entrance region Fully developed regior xd. Where we're going: Developing heat transfer coefficient relationships and correlations for internal flow Heat Transfer #2 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 2 Internal Flow Heat Transfer Where we’ve been …… • Introduction to internal flow, basic concepts, energy balance. Where we’re going: • Developing heat transfer coefficient relationships and correlations for internal flow ro

Internal Flow Heat Transfer KEY POINTS THIS LECTURE Convection correlations Laminar flow Turbulent flow Other topics Non-circular flow channels Concentric tube annulus Heat Transfer #3 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 3 Internal Flow Heat Transfer KEY POINTS THIS LECTURE • Convection correlations – Laminar flow – Turbulent flow • Other topics – Non-circular flow channels – Concentric tube annulus

Convection correlations:laminar flow in circular tubes 1.The fully developed region from the energy equation,we can obtain the exact solution. for constant surface heat flux hD Nup= =4.36 q"=C k for constant surface temperature hD Nup= k =3.66 T、=C Note:the thermal conductivity k should be evaluated at T Heat Transfer #4 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 4 Convection correlations: laminar flow in circular tubes • 1. The fully developed region from the energy equation,we can obtain the exact solution. for constant surface heat flux for constant surface temperature Note: the thermal conductivity k should be evaluated at . 4.36 k hD NuD q s C 3.66 k hD NuD Ts C Tm
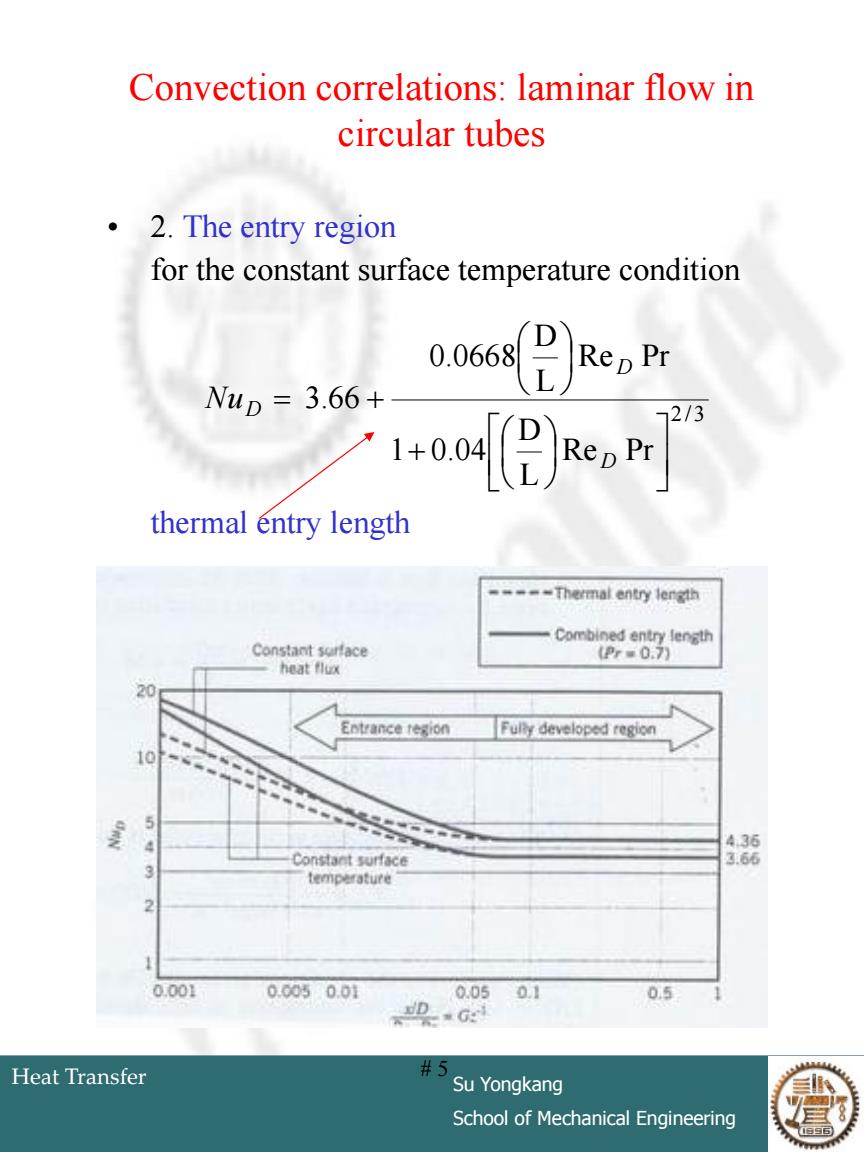
Convection correlations:laminar flow in circular tubes 0 2.The entry region for the constant surface temperature condition Rep Pr Wup=3.66+ 72/3 人1 1+-0.04Rep Pr thermal entry length ----Thermal entry length Combined entry length Constant sorface (Prs0.7) heat flux 20 Entrance region Fulty developed region 10 4.36 Constant surface 3.66 temperature 2 0.001 0.c050.01 0.0501 0.5 Heat Transfer #5 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 5 Convection correlations: laminar flow in circular tubes • 2. The entry region for the constant surface temperature condition thermal entry length 2/3 Re Pr L D 1 0.04 Re Pr L D 0.0668 3.66 D D NuD

Convection correlations:laminar flow in circular tubes .2.The entry region(cont'd) for the combined entry length 0.14 ·For values of [RepPr/(L/DΨ(u/u,P4}≥2 T.=C 0.48≤Pr<16,700 0.0044<(u14,)<9.75 All fluid properties evaluated at the mean T Tm =(Tmi+Tm.o)/2 Heat Transfer #6 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 6 Convection correlations: laminar flow in circular tubes • 2. The entry region(cont’d) for the combined entry length • For values of 1/3 0.14 / Re Pr 1.86 s D D L D Nu Re Pr/( / ) / 2 1/3 0.14 D L D s All fluid properties evaluated at the mean T / 2 Tm Tm,i Tm,o Ts C 0.48 Pr 16,700 0.0044 / 9.75 s

Convection correlations:turbulent flow in circular tubes A lot of empirical correlations are available. For smooth tubes,the fully developed flow Heating: Nup =0.023Res Pr4 Cooling: Nup=0.023Res Pr03 For rough tubes,coefficient increases with wall roughness.For fully developed flows Nua (f/8)ReD-1000)Pr 1+12.7f18)2(Pr23-1) Consider the entry length Short tubes NuD≈Nup,fa NuD C =1+ Nup,fd (x/D)m For liquid metals,see textbook p461. Heat Transfer #7 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 7 Convection correlations: turbulent flow in circular tubes • A lot of empirical correlations are available. • For smooth tubes, the fully developed flow Heating: Cooling: • For rough tubes, coefficient increases with wall roughness. For fully developed flows • Consider the entry length • For liquid metals, see textbook p461. 4/5 0.4 0.023Re Pr NuD D 4/5 0.3 0.023Re Pr NuD D 1 12.7( / 8) (Pr 1) ( / 8)(Re 1000)Pr 1/ 2 2/3 f f Nu D d Nu D NuD, fd or m D fd D x D C Nu Nu ( / ) 1 , Short tubes

Internal convection heat transfer coefficient (summary) 1.For laminar and fully developed flow (S 8.4.1): i.g"constant: Wup=4.36 Eq.8.53 ii.Ts constant: Wup=3.36 Eq.8.55 2.For laminar flow in entry region(before fully developed flow,§8.4.2: i.Ts constant 0.0668 Rep Pr WuD=3.66+- 213 Eq.8.56 1+004 ReoP ii.Combined entry length with full tube: ,1R 0.14 Eq.8.57 3.For turbulent and fully developed (S 8.5) i.Heating Nup =0.023Res Pr04 Eq.8.60 ii.Cooling No=0.023Re5Pr03 All fluid properties evaluated at the mean T Tm =(Tmi+Tmo)/2 Heat Transfer #8 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 8 Internal convection heat transfer coefficient (summary) 1. For laminar and fully developed flow (§8.4.1): i. q ” constant: ii. Ts constant: 2. For laminar flow in entry region (before fully developed flow, §8.4.2: i. Ts constant : ii. Combined entry length with full tube: 3. For turbulent and fully developed (§8.5) i. Heating ii. Cooling 2/3 Re Pr L D 1 0.04 Re Pr L D 0.0668 3.66 D D NuD 1/3 0.14 / Re Pr 1.86 s D D L D Nu All fluid properties evaluated at the mean T / 2 Tm Tm,i Tm,o Eq. 8.53 Eq. 8.55 Eq. 8.56 Eq. 8.57 Eq. 8.60 4/5 0.4 0.023Re Pr NuD D 4/5 0.3 0.023Re Pr NuD D NuD 4.36 NuD 3.36

Example:Oil at 150C flows slowly through a long,thin- walled pipe of 30-mm inner diameter.The pipe is suspended in a room for which the air temperature is 20 C and the convection coefficient at the outer tube surface is 11W/m2.K. Estimate the heat loss per unit length of tube. KNOWN:Oil flowing slowly through a long,thin-walled pipe suspended in a room. FIND:Heat oss pernt of the pipe, SCHEMATIC: Koom air ho=11W/m2 Tm=20℃ 1hinD 1haMD Ppe,D30m -Tm-150℃ ASSUMPTIONS:(1)Steady-state conditions,(2)Tube wall thermal resistance negligible,(3) Fully developed flow,(4)Radiation exchange between pipe and room negligble PROPERTIES:Table 4-5,Unused engine oil (Tm=150C=423K):k=0.133 W/mK. Heat Transfer #9 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 9 Example: Oil at 150℃ flows slowly through a long, thin- walled pipe of 30-mm inner diameter. The pipe is suspended in a room for which the air temperature is 20 ℃ and the convection coefficient at the outer tube surface is 11W/m2 .K. Estimate the heat loss per unit length of tube

ANALYSIS:The rate quation,for a unit length of the pipe,can be written as oym-1o) Rt where the thermal resistance is comprised of two elements, ,11 R财DDD 1,1 hi ho The convection cofficient for intemal flow,h,must be estimated from an appropriate correlation. From practical considerations,we recognize that the oil flow rate cannot be large enough to achieve turbulent flow conditions.Hence,the flow is am,and ifthe pipe is very long,the flow will be fully developed.The appropriate correlation is n p-366 h1=Nup kD=366x0.13W0.030m=162wm2K m.K The heat rate per unit length of the pipe is (150-20)°C =80.3W/m. < 1 1,1 m.K π(0.030m) 162+i W COMMENTS:This problem requires making a judgment that the oil flow will be laminar rather than turbulent.Why is this a reasonable assumption?Recognize that the correlation applies to a constant surface temperature condition. Heat Transfer #1 Su Yongkang School of Mechanical Engineering
Heat Transfer Su Yongkang School of Mechanical Engineering # 10