
€H7小脑模型神经网络辨 识及其应用
1 CH7小脑模型神经网络辨 识及其应用

要点: ·CMAC网络特点 ·改进的CMAC干式变压器卷线机跑偏信号谐波分析 ·CMAC网络对非线性函数学习过程 ·干式变压器卷线机跑偏信号谐波分析 ·跑偏信号谐波仿真与分析 ·改进的CMAC学习多维函数 ·CMAC网络辨识MATLAB仿真举例 CMAC网络原理及其应用 难点: ·CMAC网络对非线性函数学习过程 •跑偏信号谐波仿真与分析 ·改进的CMAC学习多维函数 2
2 要点: •CMAC网络特点 •改进的CMAC干式变压器卷线机跑偏信号谐波分析 •CMAC网络对非线性函数学习过程 •干式变压器卷线机跑偏信号谐波分析 •跑偏信号谐波仿真与分析 •改进的CMAC学习多维函数 •CMAC网络辨识MATLAB仿真举例 •CMAC网络原理及其应用 难点: •CMAC网络对非线性函数学习过程 •跑偏信号谐波仿真与分析 •改进的CMAC学习多维函数

7.1CMAC网络的特点 正常人的大脑是由大约1010~1012个神经元组成,神经 元有着相似的结构。每个细胞体有大量的树突(输入端) 和轴突(输出端),不同神经元的轴突与树突互连的结合 部为突轴,突轴决定神经元之间的连接强度和作用性质 ,而每个神经元胞体本身则是一非线性输入输出单元, 其非线性特性可用阈值型、分段线性型和连续的型函数 近似,如Sigmoid、tanh或高斯函数。 3
3 7.1 CMAC网络的特点 正常人的大脑是由大约1010~1012个神经元组成,神经 元有着相似的结构。每个细胞体有大量的树突(输入端) 和轴突(输出端),不同神经元的轴突与树突互连的结合 部为突轴,突轴决定神经元之间的连接强度和作用性质 ,而每个神经元胞体本身则是一非线性输入/输出单元, 其非线性特性可用阈值型、分段线性型和连续的型函数 近似,如Sigmoid、tanh或高斯函数

7.1CMAC网络的特点 小脑存在多层的神经元和大量的互连接。当小脑接 受许多来自各种传感器(如肌肉、四肢、关节、皮肤等) 的不同信号后,它利用负反馈进行广泛的选择(滤波), 使得输入活动仅限制在最活跃神经的一个最小子集,而 大多数的神经将受到限制,也即最活跃的神经抑制了不 太活跃的神经。人们对此进行深入研究,便得出了一个 数学上的描述,这就是Abus在于1972年提出的小脑模型 连接控制器(Cerebellar Model Articulation Controller, 简称CMAC)。 4
4 7.1 CMAC网络的特点 小脑存在多层的神经元和大量的互连接。当小脑接 受许多来自各种传感器(如肌肉、四肢、关节、皮肤等) 的不同信号后,它利用负反馈进行广泛的选择(滤波), 使得输入活动仅限制在最活跃神经的一个最小子集,而 大多数的神经将受到限制,也即最活跃的神经抑制了不 太活跃的神经。人们对此进行深入研究,便得出了一个 数学上的描述,这就是Albus在于1972年提出的小脑模型 连接控制器(Cerebellar Model Articulation Controller, 简称CMAC)

CMAC把多维离散的输入空间经过映射形成复杂的非线 性函数,具有三个特性: 一、利用散列编码(Hashing Coding)进行多对少的映射, 压缩查表的规模; 二、通过对输入分布信号的测量值编码,提供输出响应的 泛化和插补功能;三是通过有监督的学习过程,训练合适 的非线性函数。学习过程就是在查表过程中修正地址及每 个地址所对应的权值。 5
5 CMAC把多维离散的输入空间经过映射形成复杂的非线 性函数,具有三个特性: 一、利用散列编码(Hashing Coding)进行多对少的映射, 压缩查表的规模; 二、通过对输入分布信号的测量值编码,提供输出响应的 泛化和插补功能;三是通过有监督的学习过程,训练合适 的非线性函数。学习过程就是在查表过程中修正地址及每 个地址所对应的权值

近年来,国内外专家们采用各种频率分析开拓新的研究方 法解决实际问题。 1、波多黎各大学的Aceros Moreno Cesar A,Sanchez, William D.等利用离散的线性调频富里叶变换和标度频率 分析有效、省时地解决了复杂的大数据量的数学计算问题 2、多伦多的大学Ramirez Abner,.Gomez Pablo等提出了 基于数字拉氏变换的电磁暂态频率分析方法,并用电力系 统的实际应用事例证明了方法的有效性。 6
6 • 近年来,国内外专家们采用各种频率分析开拓新的研究方 法解决实际问题。 1、波多黎各大学的Aceros Moreno Cesar A, Sanchez, William D. 等利用离散的线性调频富里叶变换和标度频率 分析有效、省时地解决了复杂的大数据量的数学计算问题 2、多伦多的大学Ramirez Abner, Gomez Pablo等提出了 基于数字拉氏变换的电磁暂态频率分析方法,并用电力系 统的实际应用事例证明了方法的有效性

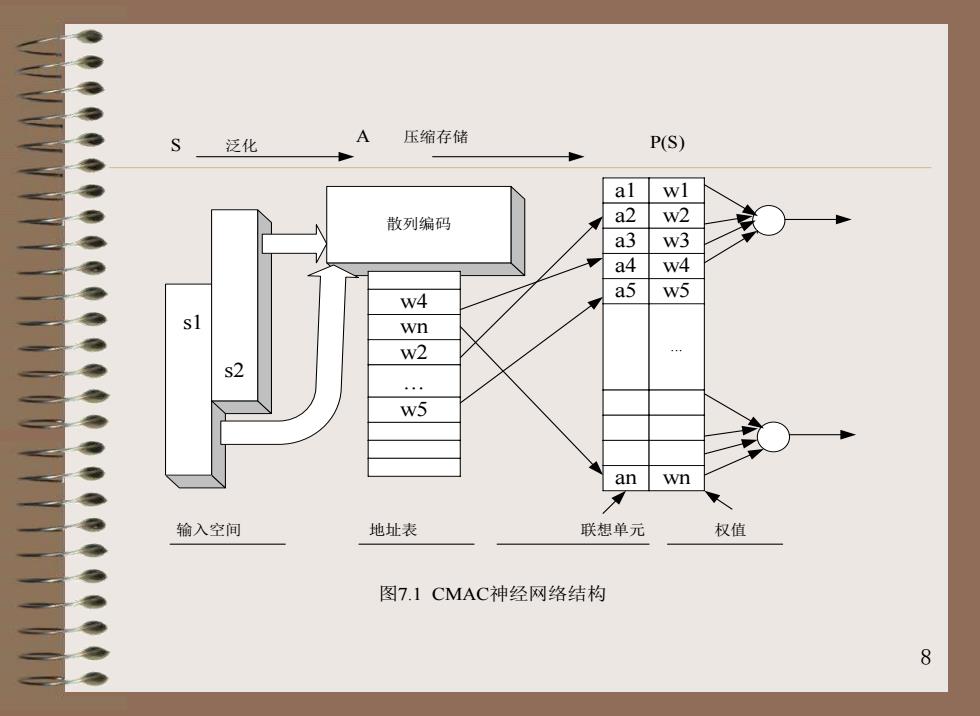
CMAC网络的结构图如图7.1所示。图中S为n维输入状 态空间,其为随机表格;A为概念存储器,它实际是散列 编码的地址表;P中的a,a2,an为实际存储器的联想单元 ,,w2,w为权值表。从S到A是由大到小的映射,从A到 P又是存储压缩映射。从而可见,CMAC实质一个智能式 的自适应查表技术,也可以描述成一个计算装置,它接 受一个输入向量S=(S,S2Sn),产生一个输出向量P=S)。 为了对给定输入状态$计算输出向量,进行了二次映射: f:S→A,g:A→P (7.1) 7
7 CMAC网络的结构图如图7.1所示。图中S为n维输入状 态空间,其为随机表格;A为概念存储器,它实际是散列 编码的地址表;P中的 为实际存储器的联想单元 , 为权值表。从S到A是由大到小的映射,从A到 P又是存储压缩映射。从而可见,CMAC实质一个智能式 的自适应查表技术,也可以描述成一个计算装置,它接 受一个输入向量 , 产生一个输出向量P=f(S)。 为了对给定输入状态S计算输出向量,进行了二次映射: 1 2 a a a , , n 1 2 , , w w wn 1 2 S (S ,S , ) Sn = f S A g A P : , : → → (7.1)
泛化 压缩存储 P(S) al wl 散列编码 w2 w4 a wn w2 s2 … w5 an wn 输入空间 地址表 联想单元 权值 图7.1CMAC神经网络结构 P
8 a1 w1 a2 w2 a3 w3 a4 w4 a5 w5 ... an wn 散列编码 w4 wn w2 ... w5 s1 s2 S 泛化 A 压缩存储 P(S) 图7.1 CMAC神经网络结构 输入空间 地址表 联想单元 权值

它把多维离散的输入空间经过映射形成复杂的非线性 函数,它具有三个特性: 一、利用散列编码Hashing Coding)进行多对少的映射, 压缩查表的规模; 二、通过对输入分布信号的测量值编码,提供输出响应 的泛化和插补功能; 三、通过有监督的学习过程,训练合适的非线性函数。 学习过程就是在查表过程中修正地址及每个地址所对应 的权值。 9
9 它把多维离散的输入空间经过映射形成复杂的非线性 函数,它具有三个特性: 一、利用散列编码(Hashing Coding)进行多对少的映射, 压缩查表的规模; 二、通过对输入分布信号的测量值编码,提供输出响应 的泛化和插补功能; 三、通过有监督的学习过程,训练合适的非线性函数。 学习过程就是在查表过程中修正地址及每个地址所对应 的权值

它把多维离散的输入空间经过映射形成复杂的非线性 函数,它具有三个特性: 在图7.1中,若输入相量元素n的个数为二,即输入S, S2,则它们激活概念存储器A中两个交叠的联想单元集合 4,4。如果希望S,的输出响应与8的输出响应有共同之 处,那么交叠就具有有利的性质。因为对S的正常响应已 经记存,对S,就能采取非常相近的响应而不必为S,再调整 权值,这种性质称为泛化(Generalition)。 10
10 它把多维离散的输入空间经过映射形成复杂的非线性 函数,它具有三个特性: 在图7.1中,若输入相量元素n的个数为二,即输入 , ,则它们激活概念存储器A中两个交叠的联想单元集合 。如果希望 的输出响应与 的输出响应有共同之 处,那么交叠就具有有利的性质。因为对 的正常响应已 经记存,对 就能采取非常相近的响应而不必为 再调整 权值,这种性质称为泛化(Generalition)。 1 2 A A, 2 S 1 S 2 S 1 S 2 S 2 S 1 S