
绝 CH3 最小二乘参数辨识 1 202414120
2024/4/20 1 CH3 最小二乘参数辨识

CH3 最小二乘参数辨识 要点: 1)最小二乘法的概念 2)一次完成的最小二乘法 3)递推的最小二乘法(适应在线辨识) 4)最小二乘遗忘因子法 5)增广的、广义的最小二乘法 2 202414120
2024/4/20 2 CH3 最小二乘参数辨识 要点: 1)最小二乘法的概念 2)一次完成的最小二乘法 3)递推的最小二乘法(适应在线辨识) 4)最小二乘遗忘因子法 5)增广的、广义的最小二乘法

单 5)增广的、广义的最小二乘法 难点: 最小二乘遗忘因子法 增广的最小二乘法 3 202414120
2024/4/20 3 5)增广的、广义的最小二乘法 难点: 最小二乘遗忘因子法 增广的最小二乘法

最小二乘法是一种经典的数据处理方法。本章 将研究最小二乘类参数辨识方法, 主要包括: •最小二乘参数估计的一次完成算法; •最小二乘递推算法; •最小二乘遗忘因子法; 4 202414120
2024/4/20 4 最小二乘法是一种经典的数据处理方法。本章 将研究最小二乘类参数辨识方法, 主要包括: •最小二乘参数估计的一次完成算法; •最小二乘递推算法; •最小二乘遗忘因子法;

增广最小二乘法; 广义最小二乘法和多级最小二乘法。 其中最小二乘的一次完成算法是最基本的, 也是现代辨识应用最广泛的一种方法,其余的 方法都是以最小二乘原理为基础推导出来的。 5 202414120
2024/4/20 5 •增广最小二乘法; •广义最小二乘法和多级最小二乘法。 其中最小二乘的一次完成算法是最基本的, 也是现代辨识应用最广泛的一种方法,其余的 方法都是以最小二乘原理为基础推导出来的

3.1最小二乘法的概念 早在1795年,著名科学家高斯就提出了最小二乘法LSM(Least Squares Method),并将其应用到了行星和彗星的运动轨道的计算中。高 斯在计算行星和彗星运动轨迹时,要根据望远镜所获得的观测数据,估 计描述天体运动的六个参数值。高斯认为根据观测数据推断未知参数时, 未知参数的最合适数值应是这样的数值,它使各次实际观测值和计算值 之间差值的平方乘以度量其精确度的数值以后和和为最小。这就是最早 的最小二乘法思想。此后,最小二乘法就被用来解决许多实际问题。针 对不同的用途,对最小二乘法进行修正,就出现了各种相应的最小二乘 算法。 6 202414120
2024/4/20 6 3.1最小二乘法的概念 早在1795年,著名科学家高斯就提出了最小二乘法LSM(Least Squares Method),并将其应用到了行星和彗星的运动轨道的计算中。高 斯在计算行星和彗星运动轨迹时,要根据望远镜所获得的观测数据,估 计描述天体运动的六个参数值。高斯认为根据观测数据推断未知参数时, 未知参数的最合适数值应是这样的数值,它使各次实际观测值和计算值 之间差值的平方乘以度量其精确度的数值以后和和为最小。这就是最早 的最小二乘法思想。此后,最小二乘法就被用来解决许多实际问题。针 对不同的用途,对最小二乘法进行修正,就出现了各种相应的最小二乘 算法

在系统辨识领域中,最小二乘法是一种基本的估计方 法。最小二乘法可用于动态系统,也可用于静态系统;可 用于线性系统,也可用于非线性系统;可用于离线估计, 也可用于在线估计。在随机的环境下,利用最小二乘法时, 并不要求观测数据提供其概率统计方面的信息,而其估计 结果,却有相当好的统计特性。最小二乘法容易理解和掌 握,利用最小二乘原理所拟定的辨识算法在实施上比较简 单。在其他参数辨识方法难以使用时,最小二乘法能提供 问题的解决方案。此外,许多用于辨识和系统参数估计的 算法往往也可以解释为最小二乘法。所有的原因使得最小 二乘法广泛应用于系统辨识领域,同时最小二乘法也达到 了相当完善的程度。 202414120
2024/4/20 7 在系统辨识领域中,最小二乘法是一种基本的估计方 法。最小二乘法可用于动态系统,也可用于静态系统;可 用于线性系统,也可用于非线性系统;可用于离线估计, 也可用于在线估计。在随机的环境下,利用最小二乘法时, 并不要求观测数据提供其概率统计方面的信息,而其估计 结果,却有相当好的统计特性。最小二乘法容易理解和掌 握,利用最小二乘原理所拟定的辨识算法在实施上比较简 单。在其他参数辨识方法难以使用时,最小二乘法能提供 问题的解决方案。此外,许多用于辨识和系统参数估计的 算法往往也可以解释为最小二乘法。所有的原因使得最小 二乘法广泛应用于系统辨识领域,同时最小二乘法也达到 了相当完善的程度
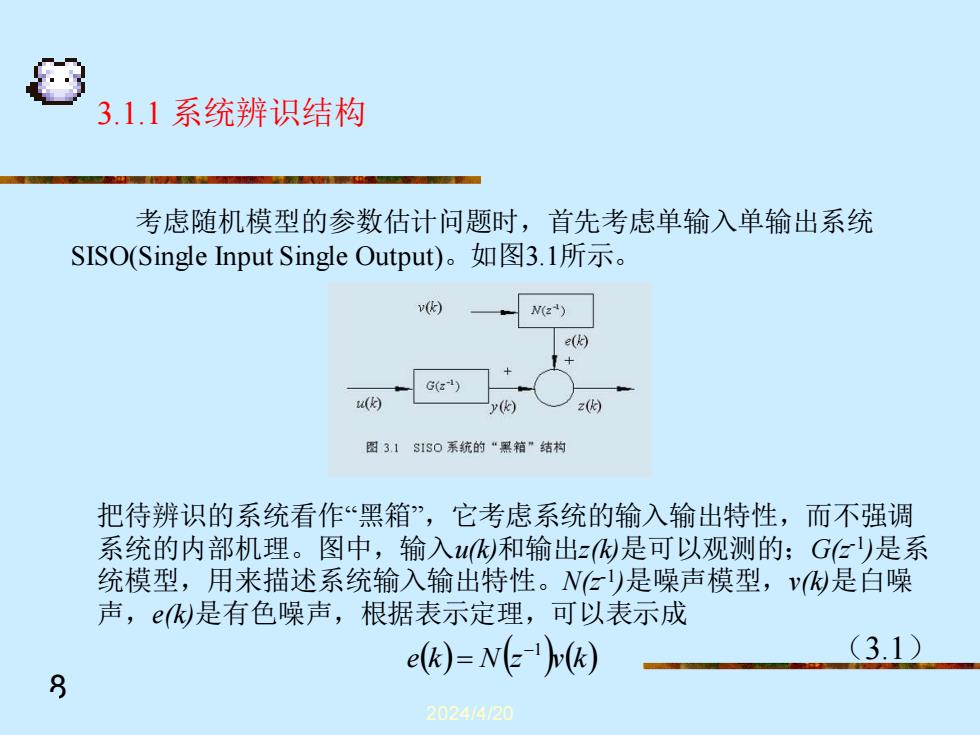
3.1.1系统辨识结构 考虑随机模型的参数估计问题时,首先考虑单输入单输出系统 SISO(Single Input Single Output)。如图3.l所示。 v(k) N(z) e( G(z) ( y() z( 图31S1S0系统的“黑箱”结构 把待辨识的系统看作“黑箱”,它考虑系统的输入输出特性,而不强调 系统的内部机理。图中,输入)和输出z)是可以观测的;GE)是系 统模型,用来描述系统输入输出特性。N仁)是噪声模型,v)是白噪 声,e是有色噪声,根据表示定理,可以表示成 e(k)=N(=-v(k) (3.1) 8 202414/20
2024/4/20 8 3.1.1 系统辨识结构 考虑随机模型的参数估计问题时,首先考虑单输入单输出系统 SISO(Single Input Single Output)。如图3.1所示。 把待辨识的系统看作“黑箱”,它考虑系统的输入输出特性,而不强调 系统的内部机理。图中,输入u(k)和输出z(k)是可以观测的;G(z-1 )是系 统模型,用来描述系统输入输出特性。N(z-1 )是噪声模型,v(k)是白噪 声,e(k)是有色噪声,根据表示定理,可以表示成 e(k) N(z )v(k) −1 = (3.1)

通常 c),- (3.2) 其中 Ae=1+a21+a222++an,2 (3.3) Bl)=b=1+bz2+.+bnem (3.4) 本章所用的系统模型总是一样的,噪声模型在各个方法中有所不 同。对实际辨识问题来说,应该选用什么样的模型,这没有一般的原 则可循。总的来说,可先选择简单的模型获得辨识结果,检验模型的 可信度,或者看实际的使用效果。如果不能满足要求,就需要换用 9 202414120
2024/4/20 9 ( ) ( ) ( ) 1 1 1 − − − = A z B z G z ( ) ( ) ( ) 1 1 1 − − − = C z D z N z ( ) ( ) = + + + = + + + + − − − − − − − − b b a a n n n n B z b z b z b z A z a z a z a z ... 1 ... 2 2 1 1 1 2 2 1 1 1 ( ) ( ) = + + + + = + + + + − − − − − − − − d d c c n n n n D z d z d z d z C z c z c z c z 1 ... 1 ... 2 2 1 1 1 2 2 1 1 1 通常 , (3.2) 其中 (3.3) (3.4) 本章所用的系统模型总是一样的,噪声模型在各个方法中有所不 同。对实际辨识问题来说,应该选用什么样的模型,这没有一般的原 则可循。总的来说,可先选择简单的模型获得辨识结果,检验模型的 可信度,或者看实际的使用效果。如果不能满足要求,就需要换用

他种模型,这时所用的辨识方法自然也就不同。也就是说解决一个实际 问题,到底应该怎样采用哪种辨识方法,这要取决于这个模型类的选择, 而模型类的确定往往需要通过多次的实验比较,最后才能确认。 3.1.2最小二乘法的基本概念 对于SISO离散随机系统,其描述方程为 zk)+azk-)+…+an,zk-n) (3.5) =bk-1)+b,4k-2)…+bk-n)+ek) 式中,(为系统输出量的第k次观测值,z(k-1)为系统输出量的第(k-1) 次观测值,以此类推。为系统第k个输入值,(k-1)为系统第(k-1)个 输入值。 10 202414120
2024/4/20 10 他种模型,这时所用的辨识方法自然也就不同。也就是说解决一个实际 问题,到底应该怎样采用哪种辨识方法,这要取决于这个模型类的选择, 而模型类的确定往往需要通过多次的实验比较,最后才能确认。 3.1.2 最小二乘法的基本概念 对于SISO离散随机系统,其描述方程为 ( ) ( ) ( ) b u(k ) b u(k ) b u(k n ) e(k) z k a z k a z k n n b n a b a = − + − + − + + − + + − 1 2 1 1 2 1 (3.5) 式中,z(k)为系统输出量的第k次观测值,z(k-1)为系统输出量的第(k-1) 次观测值,以此类推。u(k)为系统第k个输入值,u(k-1)为系统第(k-1)个 输入值