
CH5其他参数辨识方法及原理 1
1 CH5 其他参数辨识方法及原理

CH5其他参数辨识方法及原理 本章要点: 1梯度校正参数辨识原理; 2梯度校正参数辨识法的应用; 3 Bayes辨识的基本原理; 4 Bayes辨识的应用; 难点: 1梯度校正参数辨识原理; 2 Bayes辨识的基本原理; 2
2 CH5 其他参数辨识方法及原理 本章要点: 1 梯度校正参数辨识原理; 2梯度校正参数辨识法的应用; 3 Bayes辨识的基本原理; 4 Bayes辨识的应用; 难点: 1 梯度校正参数辨识原理; 2 Bayes辨识的基本原理;

CHS其他参数辨识方法及原理 5.1梯度校正参数辨识 5.2 Bayes辨识 ■53小结 3
3 ◼ 5.1 梯度校正参数辨识 ◼ 5.2 Bayes辨识 ◼ 5.3 小结 CH5 其他参数辨识方法及原理
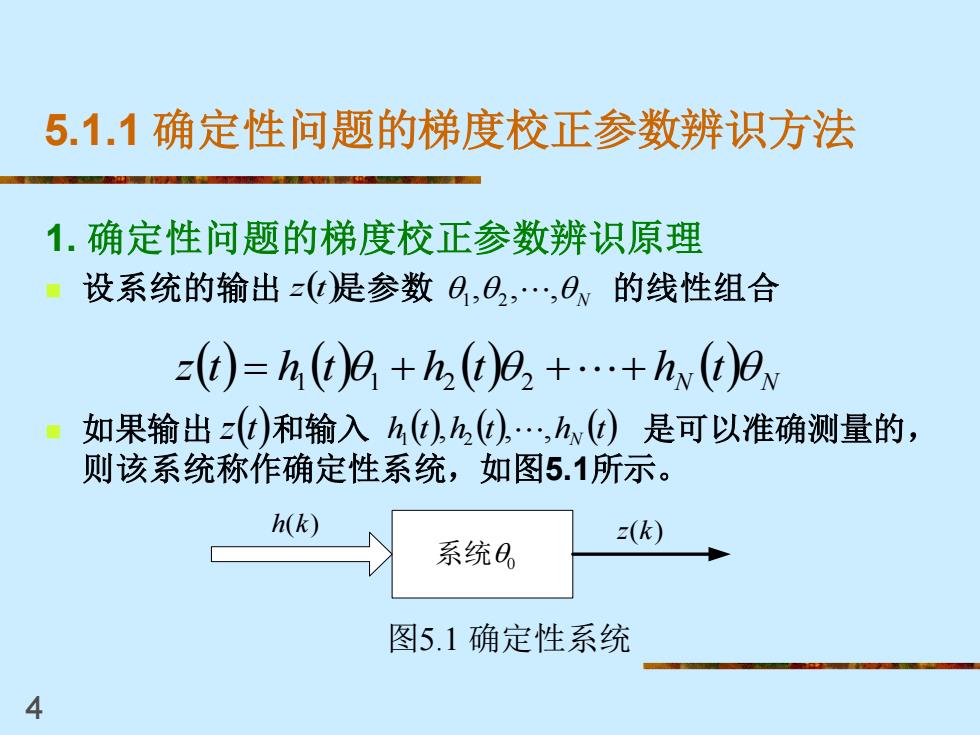
5.1.1确定性问题的梯度校正参数辨识方法 1.确定性问题的梯度校正参数辨识原理 设系统的输出z(t是参数0,O,…,0v的线性组合 zt)=h,t)9,+h,t)92++h(t)9N 如果输出zt和输入h(d),h,d),…,hw(d)是可以准确测量的, 则该系统称作确定性系统,如图5.1所示。 h(k) =(k) 系统, 图5.1确定性系统 4
4 5.1.1 确定性问题的梯度校正参数辨识方法 1. 确定性问题的梯度校正参数辨识原理 ◼ 设系统的输出 是参数 的线性组合 ◼ 如果输出 和输入 是可以准确测量的, 则该系统称作确定性系统,如图5.1所示。 ( ) ( ) ( ) ( ) N N z t = h1 t 1 + h2 t 2 ++ h t z(t) N , , , 1 2 z(t) h (t) h (t) h (t) N , , , 1 2 系统0 h(k) z(k) 图5.1 确定性系统

■设 hd)=[hd,h,d.…,hv(dI 0=[8,02,…,0y 若系统参数的真值记作日,,则有 =(t)=h'(t)0 离散化后可记为 z(k)=h(k)9 其中, h)=h(n 5
5 ◼ 设 ( ) ( ) ( ) ( ) = = T N T N h t h t h t h t , , , , , , 1 2 1 2 若系统参数的真值记作 0 ,则有 ( ) ( )0 z t h t T = 离散化后可记为 ( ) ( )0 z k h k T = 其中, ( ) ( ) ( ) ( ) T N h k h k ,h k , ,h k = 1 2

例如,用差分方程描述的确定性系统 z(k)+azk-1)+…+anzk-n)=bk-1)+…+b,4k-n) 很容易化为k)=k)只的形式,其中 h(k)=[-z(k-1...z(k-n).u(k-1)...u(k-n 10=[a,a2,…,an,b,b,…,bJ 现在的问题就是如何利用输入输出数据)和)来确定参数 0在k时刻的估计值k),使准则函数 J0)m-tei(0.k)wo (5.8) 值最小,其中 ε0,k)=zk)-h(k)e 6
6 例如,用差分方程描述的确定性系统 z(k) a z(k ) a z(k n) bu(k ) b u(k n) + 1 −1 ++ n − = 1 −1 ++ n − 很容易化为 z(k) h (k)0 的形式,其中 T = ( ) ( ) ( ) ( ) ( ) = = − − − − − − T n n T a a a b b b h k z k z k n u k u k n , , , , , , , 1 , , , 1 , , 1 2 1 2 h(k) z(k) k (k ) ^ 现在的问题就是如何利用输入输出数据 和 来确定参数 在 时刻的估计值 , ,使准则函数 ( ) ( ) ( ) k (k ) J ^ ,k ^ 2 2 1 = 值最小,其中 ( k) z(k) h (k) T , = − (5.8)

梯度校正法,即最速下降法,可以解决上述问题。 具体做法就是沿着JO)的负梯度方向不断修正k)值,直到 J⊙达到最小。梯度校正法的数学表达式为 (+1=6(k)-R(k)grad[) (5.10) 其中,Rk为N维对称矩阵,称作加权阵;gad[U(o)】 表示准则函数J旧)关于0的梯度。当准则函数⊙) 取式8时,有rad,k】 =-s(0(k).k)n(k)=-=(k)-h(k)(k)(k) (5.1) 7
7 梯度校正法,即最速下降法,可以解决上述问题。 J() (k ) ^ J() 具体做法就是沿着 的负梯度方向不断修正 值,直到 达到最小。梯度校正法的数学表达式为 ( ) ( ) ( ) ( ) (k ) k k R k grad J ˆ ˆ 1 ˆ + = − 其中, R(k) 为N维对称矩阵,称作加权阵; gradJ( ) 表示准则函数 J() 关于 的梯度。当准则函数 J() 取式(5.8)时,有 ( ) ( ) ( ) k (k ) k d d grad J ˆ 2 2 1 ˆ = , ( (k ) k )h(k ) z(k ) h (k ) (k )h(k ) T ˆ , ˆ = − = − − (5.11) (5.10)

式(5.11)代入式5.10),得 (k+1)=6(k)+R(k)h(k)(k)-h"(k)(k) (5.12) 该式就是确定性问题的梯度校正参数辨识递推公式,其权矩阵 (k)的选择是非常关键的。 8
8 式(5.11)代入式(5.10),得 (k ) (k ) R(k )h(k )z(k ) h (k ) (k ) T ˆ ˆ 1 ˆ + = + − 该式就是确定性问题的梯度校正参数辨识递推公式,其权矩阵 R(k) 的选择是非常关键的。 (5.12)

2.权矩阵的选择 权矩阵的作用是用来控制各输入分量对参数估计值的影响 程度。由式(5.12)知,输入数据向量)的各分量hk) 将直接影响参数估计值轂权矩阵俱有如下形式 R(k)=c(k)diagk)k).,k 只要选择2(),就能控制各输入分量h()对参数估计的影响。 如果选择 diag[2(k),2,(k…,v(k】=1 意味着输入分量的加权值相同,它们对参数估计值的影响 是一样的。 9
9 2.权矩阵的选择 权矩阵的作用是用来控制各输入分量对参数估计值的影响 程度。 h(k) h (k ) 由式(5.12)知,输入数据向量 的各分量 i 将直接影响参数估计值。设权矩阵 R(k 具有如下形式 ) R(k) c(k)diag (k) (k) (k) N , , , = 1 2 (k ) i h (k ) 只要选择 ,就能控制各输入分量 i 对参数估计的影响。 如果选择 diag (k) (k) (k) I 1 ,2 , ,N = 意味着输入分量的加权值相同,它们对参数估计值的影响 是一样的

至于如何合理地选择加权值k,这需要视具体问题而定。 权矩阵中的标量ck)由工程经验给出,由于,(k) 是有界的值,其下界00 ∑,kh) 10
10 至于如何合理地选择加权值 (k ) i ,这需要视具体问题而定。 权矩阵 R(k) 中的标量 c(k) 由工程经验给出,由于 (k ) i 是有界的值, (k) 0 L 其下界 且上界 H (k)1 , ,则 0 (k) (i 1,2, ,N) L i H = 另外考虑到样本的取值个数 N ,一般取 c(k) 为 ( ) ( ) ( ) = = N i i i k h k c k 1 2 1 c(k) 0