内容提要 第7章 。异步电动机三相数学模型 ·异步电动机动态数学模型的性质 基于动态模型的异步电动机调速系统 。坐标变换 。异步电动机在正交坐标系上的动态数学模型 。异步电动机按转子磁链定向的矢量控制系统 ·异步电动机按定子磁链控制的直接转矩控制系统 ·直接转矩控制系统与矢量控制系统的比较 7.1异步电动机的三相数学模型 。假设 (1)忽略空间诺被,三相绕组对桥,产生的融动势沿气隙按正弦规律分 布。 目西也 (2)忽略藏路饱和,各绕短的自感和互感都是恒定的, (3)忽略铁心损耗, (4)不考虑须率变化和温度变化对绕组电阻的影响。 (5)无论异步电动机特子是绕战型还是纯型的,都可以等效成三相镜线 转子,并折第到定子侧,后的 异步电动机运行原理 三相异步电动机的物理模型 定子三相绕组轴线 B、C在空间是固定的, 口异步电动机原 转子绕组粕线、b、c 始模型两个坐 随转子旋转。 标系! 0为n轴与A轴的夹角 如为电动机角速度 de 0=axdt 图正

.1,1异步电动机三相动态模型数学表达式 1.磁链方程 Ψ=L ·异步电动机每个绕组的磁链是它本身的自感磁链和 其它绕组对它的互感磁链之和,六个绕组的磁链可 。异步电动机的动态数学模型 用下武表示: 。磁链方程 ◆电压方程: [w L.i La 。转矩方程: ·运动方程。 :,g,各相绕组 全磁链 自感 互感 ·对于每一相绕组来说,它所交链的磁通是互感 ·互感分为两类: 磁通(主磁通)与漏感磁通之和,因此,定子 1,定子三相彼此之间和转子三相彼此之间位置都是 各相绕组自感系数为: 固定的,故互感为常值: LA L8B Lcc=L +L (7-2 2.定子任一相与转子任一相之间的位置是变化的 互感是角位移的函数。 转子各相自感为: Lu Lob Lo Lo +L L。L 与定子一相绕组交链的最大互感磁通对应的定子互感 L ,定、转子漏感 第一类互感:定子三相间或转子三相间互感 第二类互感:定、转子绕组间的互感 。因为三相绕组轴线彼此在空间 的相位差是士二,在假定磁 定子绕组任一相与转子绕 动势沿气摩被正弦规佛分布的 组任一相之间的互感,因 相对位置是变化的,互感 条件下,宜值应为 是角位移0的函数。 即有: 。定子三相间或特子三相间互感 L=Lu=Lm =Lo=Lo =Lc=L cos 6 La-bi=ha=Lu-la-be=-L LAs=L=La=Ln=Lo=Lc=L cos(0+120) (1-5) Lu=Lo Lgs Lug =Los =Lc =L cos(120-0) (7-4 当定、转子相应的两相绕组轴线重合时, 相应两者之间的互感 互感为负值,说明互感磁链起弱磁作用。 值达最大Lm

。用分块矩阵表示的磁链方程 定子电感矩阵 L.. L L 转子电感矩阵 Ψ=Li 7-8 定、转子互感矩阵 L=L 2.电压方程 c0s0-120)c0s0+1207 。三相绕组电压平衡方程 =L.cos(0+120)cos0 cos(0-120) cos(0-1209yc0s0+120 (7-9 cos0 ”,=1,R+y 式中,为定子A轴和转子a轴间的空间位移角: d d :以上两个分块矩阵互为转置 且各元素均与转子位置有关,均是 dt 变参数的,这是系镜春线性的一个 将电压方程写成矩阵形式 把磁链方程代入电压方程,展开得: 00 000 000 000 (7-12 00 其中 由于电流变化引起的脉变电动势或称变压器电动势 这更电压电流均为瞬时,链为各绕组的树金相 由于定、转子相对位置变化产生的与转速成 比的量电对势

3.转矩方程 4.运动方程 T=-,Lk+o+i6)sm0+*.+e)sm0+120 +0+i+4)sm8-l20 J do =T-T n,dt GD'dn -T.-T 物理概念:任意一相定子绕组与任意一相转子绕组间 的电磁转矩之和。 o-do 75 di 7.12异步电动机三相原始模型的性质 3.非独立性 异步电动机三相绕组为Y无中线连接,若 。1.非线性强耦合性 为A连接,可等效为Y连接。 非线性耦合体现在电压方程、磁链方程与转矩方 程。既存在定子和转子间的桐合,也存在三相绕组 ",+a+e=0 间的交叉耦合。 9。+%+9=0 is+in+ic =0 。2.非线性变参数 +4+4=0 4+ag+4=0 旋转电动势和电磁转矩中都包含变量之间的乘积, 。+6+u=0 这是非线性的基本因素。定转子间的相对运动,导 。三相变量中只有两相是独立的 ,因此三相原始数学模型并 致其夹角日不断变化,使得互感矩阵为非镜性变 不是物理对象最简洁的描述 数矩阵。 小结 (2)非线性:异步电动机无法单独对磁通进行控制,电流 ●异步电动机的数学模型的特点主要表现在以下三 个方面 (3)高阶、强精合性:三相异步电动机三相绕组存在交叉 糰合,每个绕组都有各自的电磁惯性,再考虑运动系统 ()多变量:异步电动机变压变须调速时需要进 的机电惯性,转速与转角的积分关系等,动态模型是 行电压(或电流)和频率的协调控制,有电压 个高阶系统 (或电流)和频率两种独立的输入变量。在输出 变量中,除转速外,磁通也是一个输出变量。 ◆异步电动机的动态数学模型是一个高阶、非线性, (MIMO) 强耦合的多变量系统(多输入、 多输出)

72坐标变换 72.1坐标变换的基本思路 能香将交流电动机的物理模型等效地变换成类似直 异步电动机三相原始动态模型相当复杂, 流电动机的模型? 导致异步电动机控制十分困难。简化的基本方 法就是坐标变换。 1.简化模型 2.分析得出等效直流电动机模型 1.简化模型一-非独立性 ",+9。+Ψc=0 9。+9。+Ψ。=0 在交流电动机三相对称的静止绕组A、B、C中,通 i+is +ic=0 。+%+。=0 以三相平衡的正弦电流,所产生的合成磁动势是旋 +g+4e=0 。+a+4=0 转磁动势F,它在空间呈正弦分布,以同步转速 (即电流的角频率)顺着A-B-C的相序旋转。 。非独立性:三相变量中只有两相为独立变量,完全可以消去一 。两相绕组,通以两相平衡交流电流,也能产生 相。 旋转磁动势。 所以,三相绕组可以用相互独立的 信正交时修绕组等效代替 。当三相绕组和两相绕组产生的旋特圈动静大术 。所谓独立是指两相绕组间无约束条件: 和转速都相等时,即认为两相绕组与三相绕组 。所谓对称是指两相绕组的匝数和阻值相等: 等效。 。所谓正交是指两相绕组在空间互差90度。 三相-两相变换(3/2变换) ABC台aB 2直流电动机的模型 直流电动机有电枢绕组、励磁绕组和补偿绕组,转子上的 电枢绕组通过电刷与外电略相连,通入直流电。在转子旋转 图7-3三相坐标系和两相坐标系物理模型 由。 由于电刷的, 用电 绕组产生 的磁场的 不 这种号体旋转而 浅静止的 称之为“伪静

直流电动机的励磁绕组是固定在凸极式定子上的,其产生的磁 场空间位置轴线与电枢绕组轴线相互垂直,即它们之间设有 直流电机特点:励磁和电枢各自产生磁动势空间相 可以认为主通是由师电流决定 差0度,无交叉耦合,通过励磁电流牌刺健塘,通 过电躯电流控制电感转矩。 直流电机动态数学模型:一个输入-电枢电压, 一个输出转速,可用单输入单输出的线性系镜描 他师直流电列 肠磁绕组位于直轴 轴)方向,电绕组与补偿绕组轴线位 于交轴(轴)方向上。 等效直流电动机模型 坐标变换:静止两相-旋转正交变换(2s/2r) 坐标变换:静止两相-旋转正交变换(2s/2r) aB←→dg 两个匝数相等相互正交的绕组d、4,分别通以直流电流, 产生合成磁动势下,其位置相对于绕组来说是固定的。 如果人为地让包含两个绕组在内的铁心以同步转速旋转 童动物自然也简之黄转起来,成为 若旋转磁动势的大小和转速与静止的两相交流绕组产生的 旋转磁动势相等,则旋转的直流绕组也就和静止的两相 交流绕组等效了 国74静止两相坐标系和转正交 坐标系的物理型 因此,坐标变换包括 坐标变换等效关系 三相-两相变换(3/2变换) ABC aB 如何求出ia、ig、ic与a、g和i 啊相静止-炭转正交变换(22r变典)B←→d化 之间准确的等效关系,这就是坐标 变换的任务
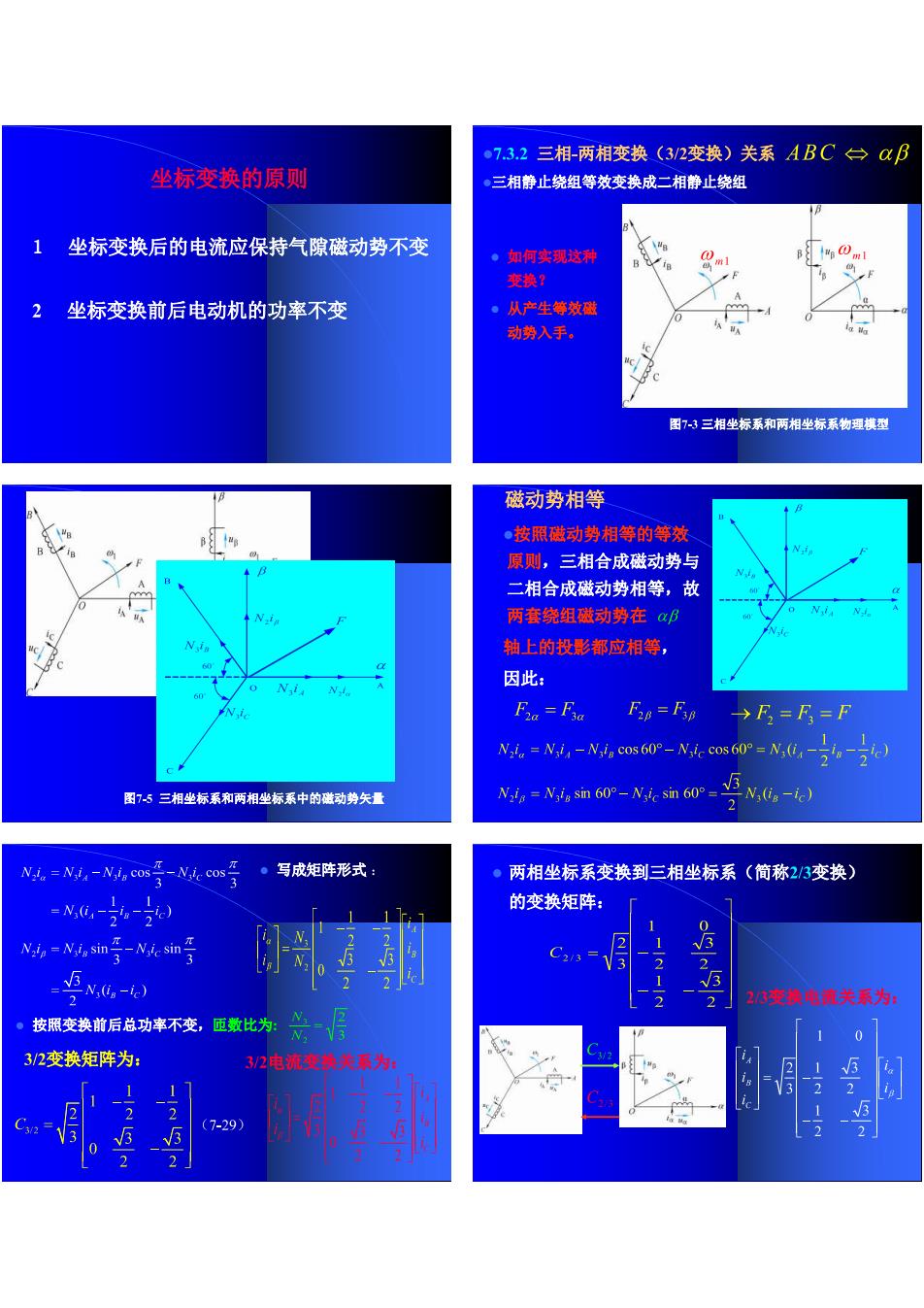
●7.3.2三相-两相变换(3/2变换)关系ABC台a阝 坐标变换的原则 ·三相静止绕组等效变换成二相静止绕组 1 坐标变换后的电流应保持气隙磁动势不变 ·如同实现这为 变换 2 坐标变换前后电动机的功率不变 ·从产生等效微 动势入平。 图73三相坐标系和两相坐标系物理横型 磁动势相等 ■按照磁动势相等的等效 原则,三相合成磁动势与 二相合成磁动势相等,故 两套绕组磁动势在a印 轴上的投影都应相等, 因此: F2n=F →F=F=F !-N cos60-N,lc cos 60=N() 图75三相坐标系和两相坐标系中的磁喇势矢量 =sin 60-N,ie sin 60N,(i-ic) N=N -cos 。写成矩阵形式 两相坐标系变换到三相坐标系(简称2/3变换) -N6-。-) 的变换矩阵: ·装照变款前后总功率不变。重康比秀兰一得 10 3/2变换矩阵为: 1 1 (7-29)
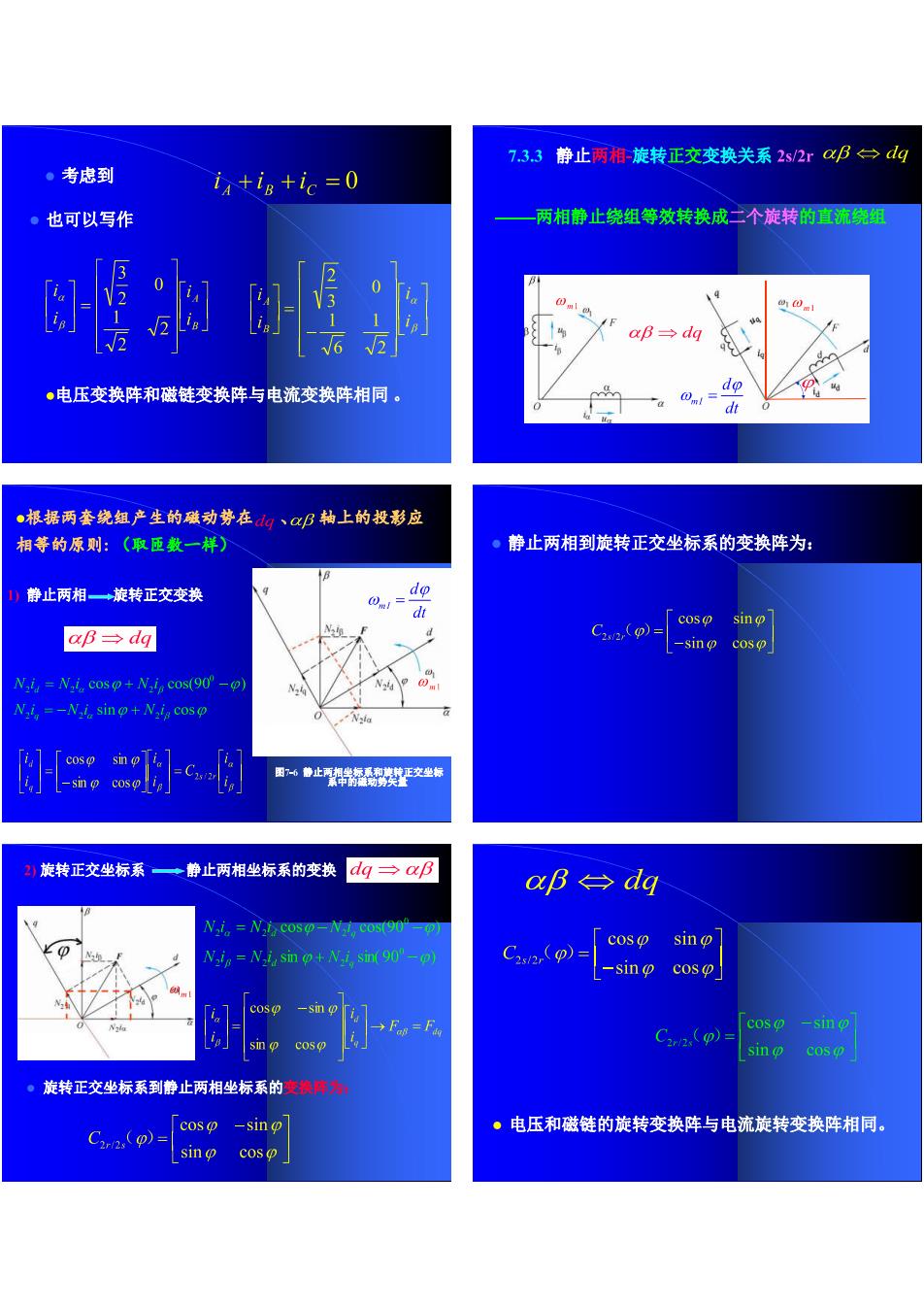
7.33静止两帽旋转正交变换关系2s/2rB台dg 。考虑到 iatin +ic=0 。也可以写作 一两相静止绕组等效转换成个旋转的直流绕组 19 a→dg 电压变换阵和磁链变换阵与电流变换阵相同 ●根据两套绕组产生的磁动势在山、αB上的投影应 相等的原则:(取匝数一样) 。静止两相到旋转正交坐标系的变换阵为: 静止两相一→莱转正交变挨 do p→dg C-csp sin c N.i-N cos+i cos(9 Ni =-i sino+N,i cos [c 燕转正交坐标系一静止两相坐标系的变换dg→ aB→dg N.=Ni cos-N cos(90 N.i=N.i sin +N.i,sin(90) C3(p) [coso sino -sin cos cos -sin C)= sin 。旋转正交坐标系到静止两相坐标系的变牌 。电压和磁链的旋转变换阵与电流旋转变换阵相同, C() cosp sin cos

7.4异步电动机在正交坐标系上的 定子三相ABC→两相aB 动态数学模型 ○首先推导静止两相坐标系中的数学模型, 转子三相abc三转子两相aB 然后推广到旋转正交坐标系。 。由于运动方程不随坐标变换而变化,故仅 讨论电压方程、磁链方程和转矩方程。 在以下论述中,下标表示定子或静止,下 标表示转子或旋转。 7.4.1静止两相坐标系中的动态数学模型 (2)磁链方程为: 1、定子绕组和转子绕组仅3/2变换后的方程m ●(1)电压方程 -L si 0 L cos 0 小结 (3)转矩方程 (1)3/2变换将按 2红分布的三相绕组等效为互相 垂直的两相绕组,消除了定子三相绕组、转子三 相绕组间的相互耨合。 T.=-npLa(i+i)sn +(iiii )cos](742) (2)定子绕组与转子绕组间仍存在相对运动,因 而定、转子绕组互感阵仍是非线性的变参数阵。 输出转矩仍是定、转子电流及其定、转子夹角的 函数。 3/2变换减少了状态变量的 子和转子的自成

2、静止两相坐标系中的方程(a) aB三aB )ne的关系: cose -sine xB→caB C2.(0= N.i,=N,i cos0-N.i,sin0 N.i=N.i sin0+N,i,cos0 N 转子两相αB→定子两相aB变换系数矩阵为 C(0)=[cos0 -sino] 2)静止两相坐标系中的电压方程(aB): 。静止两相坐标系中的磁链方程(aB): 0 DV. 。静止两相坐标系中的转矩方程 。结论: ·旋转变换改变了定、转子绕组间的耦合关系, T。=nLn(daa-iin) 7-46 将相对运动的定、转子绕组用相对静止的等效 绕组来代替,消除了定、转子绕组间夹角对磁 链和转矩的影响。 T.=-n,Ln【ii。+i)sin0+0.g-i.eos0 ·旋转变换的优点在于将非线性变参数的磁链方程 转化为线性定常的方程,但却加剧了电压方程中 7-42 的非线性耦合程度,将矛盾从磁链方程转移到电 压方程中了,并没有改变对象的非线性合性