
第3章转速闭环控制的直流调速系统 调节器:比例、积分、微分 根据自动控制原理,将系统的被调节量作为 反馈量引入系统输入端,与给定量进行比较,用 比较后的偏差值对系统进行控制,可以有效地抑 制甚至消除扰动造成的影响,从而维持被调节量 很少变化或不变,这就是反绩控制的基本作用。 在调速系统中,被调节量是转速一一构成的是转速 ()比例调节器 有静差调速 闭环控制的直流周速系统。 (2)I、PI调节器 无静差调速 S3.1有静差(比例控制)的转速闭环直流调速系统 1,转速反馈控制直流调速系统的组成 S3.1.1比例控制直流调速系统的结构与静特性 比例调节器: R =-R 图3】带转速负反馈的闭环直流调速系统原理框图 各环节稳态关系如下: 下面分析闭环调速系统的稳态特性,以 确定它如何减少转速波动。 ()电压比较环节 为了突出主要矛盾,先作如下的假定 调节器的净输入信号 (1)忽略各种非线性因素,假定系统中各 U,=U-U 环节的输入输出关系都是线性的,或者只 ()比斜调节器 取其线性工作段; U.=k,4☑ (2)忽略控制电源和电位器的内阻。 3)测速反馈环节U,=am
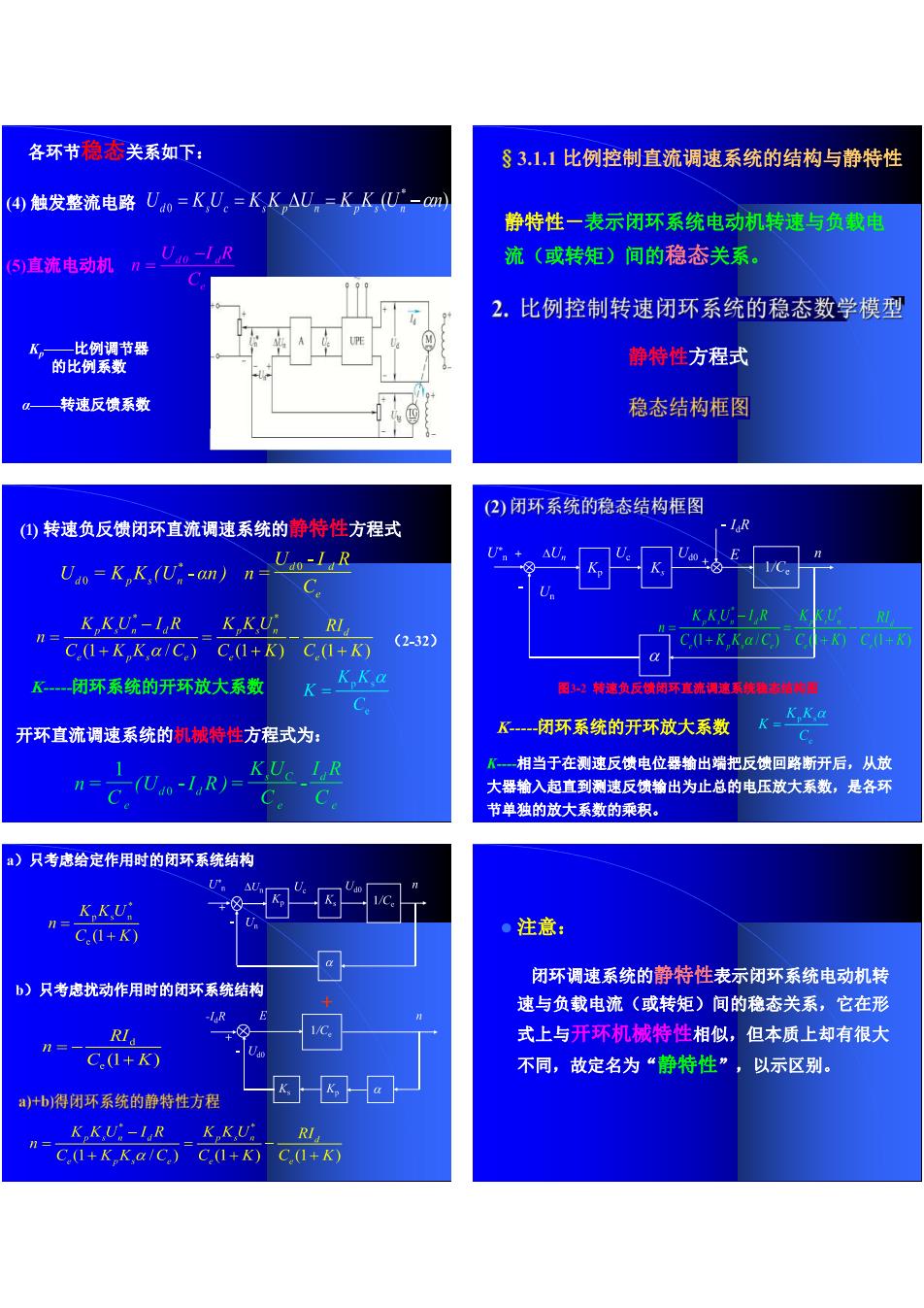
各环节稳态关系如下: S3.1,1比例控制直流调速系统的结构与静特性 4触发整流电路Un=KU=KK△U=KK(U广-am) 静特性一表示闭环系统电动机转速与负载电 5)直流电动机=U一, 流(或转矩)间的稳态关系。 2.比例控制转速闭环系统的稳态数学模型 静特性方程式 转速反债系数 稳态结构框图 (②)闭环系统的稳态结构框图 ()转速负反馈闭环直流调速系统的静特性方程式 Uo=K,K,Ui-an)n Uo-1R C KKU-IRKKU RI /C)C()C.(G) K闭环系统的开环放大系数 磨小特南负反净明醉重满调童成纳非地角门 开环直流调速系统的机城特性方程式为: …闭环系统的开环放大系数 K= n= -(Un-1R)-KU LR K一相当于在测速反馈电位器输出端把反馈回路断开后,从放 大器输入起直到测速反馈输出为止总的电压放大系数,是各环 节单独的放大系数的乘积。 )只考虑给定作用时的闭环系统结构 KK.U' C+K) 注意 b)只考虑扰动作用时的闭环系统结构 闭环调速系统的静特性表示闭环系统电动机转 速与负载电流(或转矩)间的稳态关系,它在形 式上与开环机械特性相似,但本质上却有很大 不同,故定名为“静特性”,以示区别。 ab)得闭环系统的静特性方程 KKU:-IR KKU; n-CIC)C0万 C+)

-R 53.12开环系统与闭环系统的特性的对比分析 -IR 而闭环时的静特性可写成 1、性能指标对比分析 如果断开反馈回路,则上述系统的开环机城特性为: KKU._ C0 (3.3 % =6p-n3-2 C 比较式(3-2)和式(3-3)不难得出以下的论断: (2)如果比较同一个开环和闭环系统,则闭环系统 的静差率要小得多, ()闭环系统静特性可以比开环系统机械特性硬得多。 闭环系统和开环系统的静差率分别为 在同样的负载扰动下,两者的转速降落分别为 Sd= △和 RI. An C0+ 它们的关系是 当mp=e时 (3-5) K (34 (3)当要求的静差率一定时,闭环系统可以大大提 高调速范围, 概括起来,可得下述结论: 如果电动机的最高转速都是m:而对最低速静 要取得上述三项优势,都取决于一点,闭环系统 差率的要求相同,那么: 必须设置放大器,且K要足铭大。 开环时,“司 闭环时,司 闭环调速系统可以获得比开环调速系统硬得多 的稳态特性,从而在保证一定静差率的要求下,能 再考虑式 1+K 够提高调速范围,为此须增设调节器以及检测与反 馈装置 Da=(l+K)Dp 3-6

S3,12开环系统与闭环系统的特性对比分析 2、开环系统机城特性与闭环系统静特性对比分析 开环系统,负载增加↑→ n-ao-1aR C 。比例控制的闭环调速系统可以获得比开环系统 硬得多的稳态特性,即负领增加的转速 客减小了 闭环系统: 。问题:闭环系统负载波动时转速变化 负载增加,↑→+ 为什么会减小了呢? 开环系统机械特性和闭环系统静特性的关系 R 开环系统机城性 D 由此看来,闭环系统能够减少稳态速 的实质在于它的自动调节作用,在于它能 随着负载的变化而相应地改变电枢电压, 以补偿电枢回路电阻压降。 ●例题3-1 片!有静楚调速票统突加负教过划 S3.1.3有静差闭环系统动态过程 在例题2-2中,龙门创床要求D=20,s<5%, 已知K=30,a=0.015 V.min/r,.C。=0.2Vmi 比例控制为什么是有静差的 如何采用比例闭环系统满足此要求? 解:在上例中已经求得:△np=275r/min, 但为了满足调速要求,须有△m=2.63r1min, 由式(34)可得 275 a 代入已知李,则得K,一K己 036 30×0.0150

S3.1.4闭环调速系统的反馈控制规律 S3,1.4闭环调速系统的反馈控制规律 1,比例控制系统是被调量有静差的调速系统 闭环时的静特性为: 转速反馈调速系统是一种基本的反馈控制系 -A 统,它具有以下三个基本特征,也就是反馈控制 =M 63 C.0+K0C.0+K0 的基本规律,各种不另加其他调节器的基本反惯 采用比例放大器,闭环系统的开环放大系数 控制系统都服从于这些规律」 值越大,系统的稳态性能越好。然而,闭环系统的稳 态速整为: Ar-C.0+K) 只有 ,才能使△=0,而这是不可能的。因此,这 样的调速系统叫做有静差调速系统。 S3.1.4闭环调速系统的反馈控制规律 ■调速系统的扰动源 2,服从给定,抵抗扰动 负载变化的扰动(使1变化); 交流电源电压波动的扰动(使K变化); 。找动—除给定信号外,作用在控制系统各环节 上的一切会引起输出量变化的因素都叫做“扰动作 电动机励磁的变化的扰动(造成C变化): 用”。 -放大器输出电压漂移的扰动(使K变化); 温升引起主电路电阻增大的扰动(使变化) 检测误差的扰动(使a变化)。 ,变化 ▣抗扰能力分析K。变 电源被动 电变化 电阻变化 变化 爵盛变化 a 检海误若 检意误是 图3一4闭环调速系续的给定作用和扰动作用 。雕是,如果在反续通道上的测速反绩系数受到某种影响而发 例如:→d0l→d→Um→ant 生变化,它非但不能得到反馈控制系统的抑制,反而会增大 被调量的误差, mt←La0↑eCet -例如:a→↑→A,↓→U↓→Um↓→mk 。反馈控制系统对被反馈环包围的前向通道上的找 因此,反锁控制系统所能抑制的只是被反锁环包固的前向 动都有抑制功能, 通道上的扰动

■给定作用 变化 R上 反馈控制系统具有良好的抗扰性能,它能 有效地抑制一切被负反馈环所包围的前向通 道上的扰动作用,但对给定作用则是唯命是 检清视出 从的。 与众不同的是在反锁环外的给定作用,如图中的 转速给定信号,它的些徽变化都会使被调量随之 变化,丝毫不受反馈作用的抑制。 S3.1.4闭环调速系统的反馈控制规律 ■结论: 3.系统的精度依赖于给定和反馈检测精度 给定精度一由于给定决定系统输出,输出精度自然取 反馈控制系统的规律是:一方面能够有 决于给定精度 效地地制一切被包围在负反幢环内邮向通 如果产生给定电压的电源发生波动,反债控制系统无 法鉴别是对给定电压的正常调节还是不应有的电压波动, 道上的忧功作用: 因此,高精度的调速系统必须有更高精度的给定稳压电 另一方面,紧紧地跟随着给定作用,对 源。 给定信号的任何变化都是唯命是从的。 检测辅度 一反绩检测装置的误差也是反债控制系统无 法克服的,因此检测精度决定了系统输出精度。 S3.1.5比例控制转速闭环系统的稳定性分析 §3,15比例控制转速闭环系统的稳定性分析 1比例控制直流调速系统的动态数学模型 。问题:增加比例调节器的比例系数,可以减小转速 、一个带有储能环节的线性物理系统的动态过程可以用线 降落,从而扩大调速范围。 性微分方程措述 5 。微分方程的解即系绕的动志过耀,它包括两部分:暂态 比钢系数可以感 响应和稳态响应。 。在动态过程中,从施加给定输入值的时刻开始,到输出 生意:设计系统首先要保证系统是稳定的】 达到稳态值以前,是系统的动态响应, 。系统达到稳态后, 可用稳态解来描述系统的稳态特性
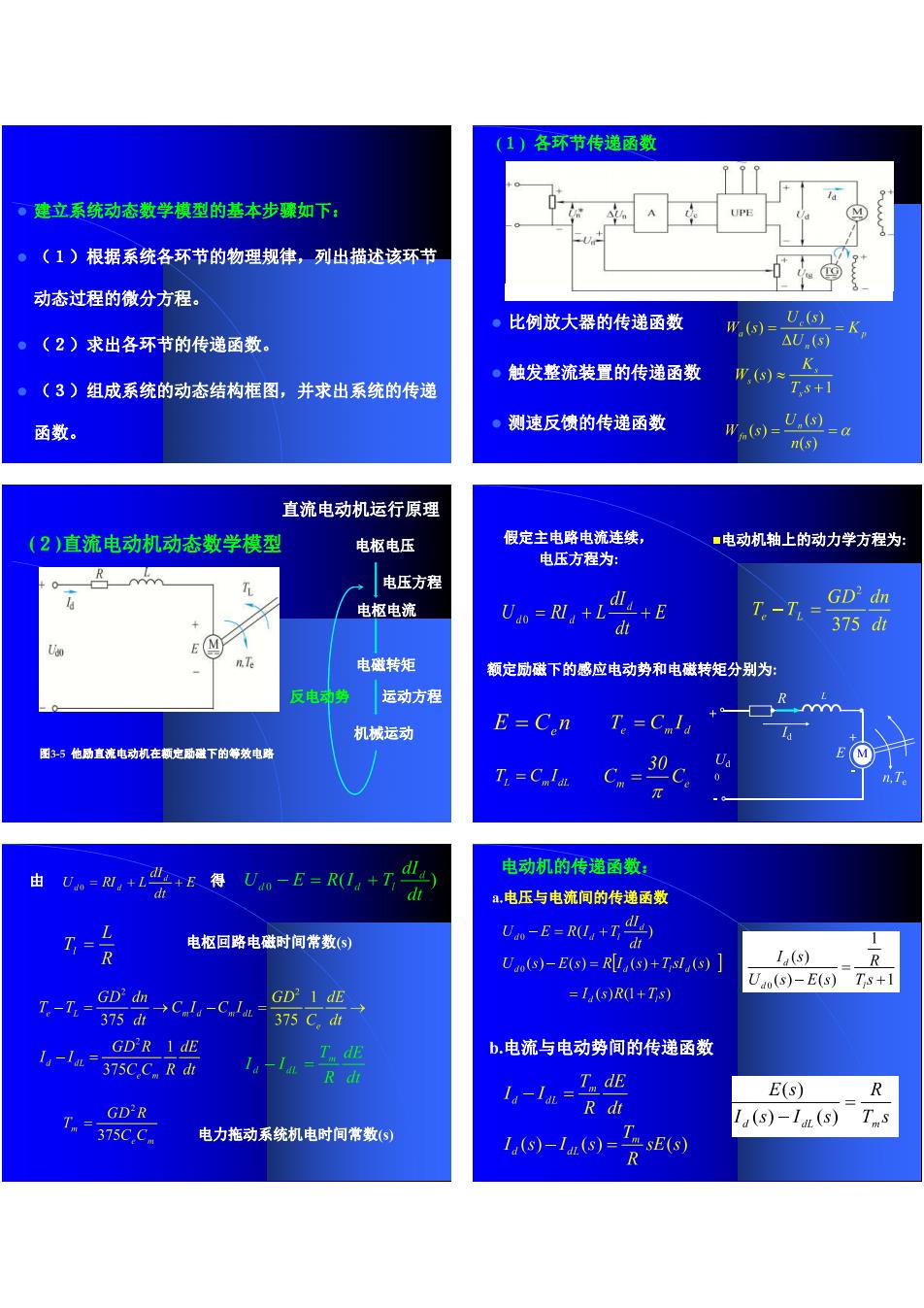
(1)各环节传递函数 。建立系统动态数学模型的基本步骤如下 ·(1)根据系统各环节的物理规律,列出描述该环节 动态过程的徽分方程。 ·比例放大器的传递函数 U.(s) 。(2)求出各环节的传递函数。 触发整流装置的传递函数 。(3)组成系统的动态结构框图,并求出系统的传递 函数。 ·测速反馈的传递函数 n(s) 直流电动机运行原理 (2)直流电动机动态数学模型 电据电压 假定主电路电流连续, ■电动机轴上的动力学方程为 电压方程为: 电压方程 Uw=刷+L GD dn 电枢电流 -+E T.-T=35d (M 电转矩 额定励磁下的感应电动势和电磁转矩分别为: 运动方程 R 机械运动 E=Cn T.=Cl 图35他扇直流电动机在 定磁下的等效电路 Tr =Cala 电动机的传递函数: 品,电压与电流间的传递函数 电枢回路电磁时间常数(付 -f,7尝 U)-E=R,+T,s)] L(s) GD'I dE =1()R+T Uao(s)-E(s)Ts+1 375d 375C,d GD'R I dE 1,-a-375C.C.R d T.de b.电流与电动势间的传递函数 R di E(s) R GD'R T.=375C.C. Rd山 I.(s)-Ia(s)Ts 电力施动系统机电时间常数何 1,-10= -sE(s)

直流电动机的动态结构框图 直流电动机的动态结构图 ) E(s) /-E药R 1s) U0(s)-E(s)Ts+1 ES) + 89 E(s) 》式(315)的结构国 切式(316的结构国 )整个直流电动 图36额定最磁下直流电动机动态结构国 ■结构图的变换和简化 额定励磁下的直流电动机是一个二阶线性环节, 1/R 17 IC. Uao(s)T.Ts+T.s+1 在结构图中显现出电流,可将扰动量 由特征方程知:当T。>7时, 再进行等效变换,得下图 U一n间可以分解成两个惯性环节 R(Ts+1) 当T。<4时, i(). IC. 电动机是一个二阶晨荡环节。 +Tos+1 (③)闭环调速系统的动态结构图及传递函数 (6)系统的传建函数 (:)对春结构图 设1=0,从给定输入作用上看 KK IC Ua(s) )_ T.T,s2+Ts+1 KK C,(1+K) 图8闭环调速系续的动态结构图 + 1+K 1+K

S3,1.5比例控制转速闭环系统的稳定性分析 根据三阶系统的劳斯-赫尔维茨(ROuh 2,比例控制直流调速系统的稳定性分析 Hurwit2)判据,系统稳定的充分必要条件是 KK. 路受 C(1+K) a,>0,a>0a,>0,4,>04,4-a,4,>0 1+K> 1+K 1+K 闭环直流调速系统的特征方程为: 式(3-21)的各项系数显然都是大于零的 因此稳定条件就只有: 10 1+K + TI+T)T。+TTT 它的一般表达式为 1+K T+T,+T)>+K0 dos'+as'+as+a; 整理后得 例题3-2 在例愿31中,系统采用的是三相桥式可控 K= 际作系统的临界放大系数 .TT 整流电路,已知电枢回路总电阻R-0,18Q, 电感量L=3mH,系统运动部分的飞轮惯 当K之Kcr时,系统将不稳定 量GD2=60N·m2,试判别系统的稳定性。 对于一个自动控制系统来说,稳定性是它能否正常工 作的要条件,是必须保证的 这与稳态误差对K的要求是矛盾的。 解: 例题3-3 。电磁时间常数 T--00-00167 在上题的闭环直流调速系统中,若改用全 。机电时间常数 GD'R 60x0.18 T.-37CC.- 控型器件的PVM调速系统,电动机不变, 电枢回路参数为:R=010,L=1mW,K,=44 。晶闸管装置的滞后时间常数为 PVM开关频率为8kh。按同样的稳态性能 7=0.0016 。为保证系统稳定,应满足的稳定条件 指标D=20,8≤5%,该系统能否稳定? 如果对静差率的要求不变,在保证稳定时 系统能够达到的最大调速范围有多少? 闭环系统的动态稳定性和例题3-1中稳态性能要求 K≥103.5是矛盾的

解: (1)该系统能否稳定? ●按照稳态性能指标D=20、s≤5%要求 △nys2.63tmin (见例题22) 60x0.1 =0.0417s 而M调速系统的开环额定速降为: 0.2 7=80=00o125s 1=5 。按系统稳定性要求应有。 K=-1≥1525 An. 2.63 20 D=- 1000×0.05 偏差是维系系统运行的基础,必然要产生静差, 属于有静差系统。 。可见,PWM调速系统的稳态性能指标可以比2 系统大大提高。 能否实现无静差调速 如果要消除系统误差,必须寻找其他控制方 法,比如:采用积分(Integration)调节器或比 例积分(PI)调节器来代替比例放大器。 如何实现无静差调速? 本节将讨论,采用积分(1)调节器或 比例积分(P)调节器代替比例放大器 ●调节器选择P? I? PI? ,构成无静差调速系统