
3引试球以下序列因的装分A、y与求和立0 0,k<0 =分≥0 解 ()的闭式表达式为 f)=(与)() ()=fk+1)-f)=(5)ε(k+)-(分)6() 0,k<-1 =(分2&(k+)-(k]=1,k=-1 -(分",k≥0 =f-fk-)=(宁ε)-学“ek-) 0,k<0 =(宁)[s(k)-2(k-1】=1,k=0 立0-2的a刻=吃rr 0,k<0 =2-(5)()= 2-(,k≥0 32求齐次差分方程的解,)-k-》=00)=1 解: 此方程的齐次解为 陶=C分,k20 将初始条件代入得 0)=C(°=C=1 则齐次方程的解为 )=分a) 3.3求以下齐次差分方程的解: k)-2k-1)+2(k-2)-2k-3)+yk-4)=0, y0)=0,y(1)=1,y2)=2,y3)=5
3.1 试求以下序列 f (k) 的差分f (k) 、f (k) 与求和 k i f (i) 。 f (k) ) , 0 2 1 ( 0, 0 k k k 解: f (k) 的闭式表达式为 ) ( ) 2 1 f (k) ( k k ) , 0 2 1 ( 1, 1 0, 1 ( 1) ( )] 2 1 ) [ 2 1 ( ) ( ) 2 1 ) ( 1) ( 2 1 ( ) ( 1) ( ) ( 1 1 k k k k k f k f k f k k k k k k k ) , 1 2 1 ( 1, 0 0, 0 ) [ ( ) 2 ( 1)] 2 1 ( ) ( 1) 2 1 ) ( ) ( 2 1 ( ) ( ) ( 1) ( 1 k k k k k f k f k f k k k k k k k ) , 0 2 1 2 ( 0, 0 ) ] ( ) 2 1 [2 ( ) ] ( ) 2 1 ) ( ) [ ( 2 1 ( ) ( 0 k k k f i k k k k k i k k i k k i 3.2 求齐次差分方程的解: ( 1) 0, (0) 1 2 1 y(k) y k y 。 解: 此方程的齐次解为 ) , 0 2 1 y(k) C( k k 将初始条件代入得 ) 1 2 1 (0) ( 0 y C C 则齐次方程的解为 ) ( ) 2 1 y(k) ( k k 3.3 求以下齐次差分方程的解: y(k) 2 y(k 1) 2y(k 2) 2y(k 3) y(k 4) 0, y(0) 0, y(1) 1, y(2) 2, y(3) 5

解:已知差分方程的特征方程为 1-22+22-21+1=0 (22+12-1)2=0 解特征根为2=与入4=1 令)=Ck+C,)+Dcor(受)+D,sm5 将0)=00=12)=23)=5代入得 [C。+D=0 C,=2 JC+C。+D,=1 JC6=-1 2℃+C-D-2 D=1 3C1+C。-D=5D=0 =2-1+cwk≥0 3.4求下列差分方程所描述的LTΠ离散系统的零输入响应。 (2))+2k-)+k-2)=f)-fk-1),(-=1-2)=-3 解:零输入响应满足方程 y,(k)+2y(k-1)+y,(k-2)=0 特征根为入=入=-山故齐次解为 y(k)=C(-I)+Ck(-1),k20 将初始值代入,得 y,(-)=-C+C2=1 y,(-2)=C1-2C2=-3 由以上两式可解得9,=1,C,=2,得该系统的零输入响应 y,()=[-I)+2k(-)]s(k)=(2k+1(-)ε() 3.6求下列差分方程所描述的离散系统的零输入响应、零状态响应和全响应。 (2)Jk)+2k-1)=f(k),fk)=2,(),W-1)=1 解 yk)-2yk-1)=0 零输入响应(-)=-1 y0)=-2y(-1)=-2 特征方程 +2=0y(k)=C(-2) 由0)=-2得C=-2 y,(k)=(-2)k≥0 零状态响应 k)+2k-1)=2(k) -)=1
解:已知差分方程的特征方程为 2 2 2 1 0 4 3 2 ( 1)( 1) 0 2 2 解特征根为 j 1,2 1 3,4 令 ) 2 ) sin( 2 ( ) ( ) ( 1 0 1 0 y k C k C D cox k D k 将 y(0) 0 y(1) 1 y(2) 2 y(3) 5 代入得 0 1 1 2 3 5 2 2 1 0 0 1 0 1 1 0 0 1 0 1 1 0 1 0 1 D D C C C C D C C D C C D C D ), 0 2 ( ) 2 1 cos( k k y k k 3.4 求下列差分方程所描述的 LTI 离散系统的零输入响应。 (2) y(k) 2y(k 1) y(k 2) f (k) f (k 1), y(1) 1, y(2) 3 解:零输入响应满足方程 y (k) 2y (k 1) y (k 2) 0 x x x 特征根为 1, 1 2 故齐次解为 ( ) ( 1) ( 1) , 0 y k C1 C2 k k k k x 将初始值代入,得 ( 2) 2 3 ( 1) 1 1 2 1 2 y C C y C C x x 由以上两式可解得 1, 2, C1 C2 得该系统的零输入响应 y (k) [( 1) 2k( 1) ] (k) (2k 1)( 1) (k) k k k x 3.6 求下列差分方程所描述的离散系统的零输入响应、零状态响应和全响应。 (2) y(k) 2 y(k 1) f (k), f (k) 2 , (t), y(1) 1 k 解: 零输入响应 ( 1) 1 ( ) 2 ( 1) 0 y y k y k y(0) 2y(1) 2 特征方程 k 2 0 yzi (k) C(2) 由 y(0) 2得 C 2 ( ) ( 2) 0 1 y k k k zi 零状态响应 ( 1) 1 ( ) 2 ( 1) 2 ( ) y y k y k k k

y(k)=-2y(k-1)+2ε(k) y(0)=-2y(-I)+1=-1 特解为'(=P2 代入方程 Pm+2P2=2P= ∴y(k)=2-,k≥0 y(k)=C2(-2)+2 0)=C+- C-3 y(k)=3(-2)-+2,k≥0 全响应为: y(k)=y(k)+y (k) =(-2)1+3(-2)+2 =7(-2)-+2-,k≥0 4)+3k-)+2k-2)=f),f)=(),-1)=1-2)=0 解: 零输入响应 [y(k)+3yk-1)+2k-2)=0 1(-1)=1,1W-2)=0 y(0)=-3y(-1)-2(-2)=-3 y0=-3y0)-2(-1)=7 特征方程2心+3孔+2=0,特征根为入=-山入=-2 设y(k)=C,(-)+D,(-2) 由0)利0可得 ∫C+D=-3 y(k)=(-1)-4(-2),k≥0 零状态响应 [yk)+3k-1)+2k-2)=(k) (-1)=1-2)=0 yk)=-3k-1)-2k-2)+(k) 0)=-2 y)=5
(0) 2 ( 1) 1 1 ( ) 2 ( 1) 2 ( ) zs zs k zs zs y y y k y k k 特解为 k y p (k) P2 代入方程 ( ) 3( 2) 2 , 0 2 3 1 2 1 (0) ( ) ( 2) 2 ( ) 2 , 0 2 1 2 2 2 2 1 1 2 2 1 2 1 1 y k k C y C y k C y k k P P P k k zs zs k k zs k p k k k 全响应为: 7( 2) 2 , 0 ( 2) 3( 2) 2 ( ) ( ) ( ) 1 1 1 1 1 k y k y k y k k k k k k zi zs (4) y(k) 3y(k 1) 2y(k 2) f (k), f (k) (k), y(1) 1, y(2) 0 解: 零输入响应 ( 1) 1, ( 2) 0 ( ) 3 ( 1) 2 ( 2) 0 y y y k y k y k (1) 3 (0) 2 ( 1) 7 (0) 3 ( 1) 2 ( 2) 3 y y y y y y 特征方程 3 2 0, 2 特征根为 1, 2 1 2 设 k k yzi (k) C ( 1) D ( 2) 1 1 由 y(0)和y(1) 可得 4 1 2 7 3 1 1 1 1 1 1 D C C D C D y (k) (1) 4(2) , k 0 k k zi 零状态响应 ( 1) 1, ( 2) 0 ( ) 3 ( 1) 2 ( 2) ( ) y y y k y k y k k (1) 5 (0) 2 ( ) 3 ( 1) 2 ( 2) ( ) y y y k y k y k k
将特解",)=P代入得P+3P+2P=1 P活 y,W)=石k20 =C-+(-2r+ 由0)及()得 1 c-2n+名5a-号 =--2r+名≥0 全响应为: y(k)=y(k)+y(k) r-9-2+20 3.10求下图所示系统的单位序列响应。 八 D 解:设左端加法器的输出为(),则相应延迟单元的输出为xk-),(k-2小由左边加法 器的输出可得 xk)=fK)+4x(k-1)-3x(k-2) 多 f(k)=x(k)+4x(k-1)-3x(k-2) 由右端加法器输出可得 k)=3x(k)-x(k-1) 由上式可得 -4k-1)=3-4x(k-1】-[-4x(k-2] 3k-2)=33x(k-2]-[3x(k-3) 将以上三式相加可得 k)-4y(k-1)+3k-2) =3[x(k)-4x(k-1)+3x(k-2】-[x(k-)-4x(k-2)+3.x(k-3) 考虑到f)=xk)+4x-)-3k-2),可得系统的方程
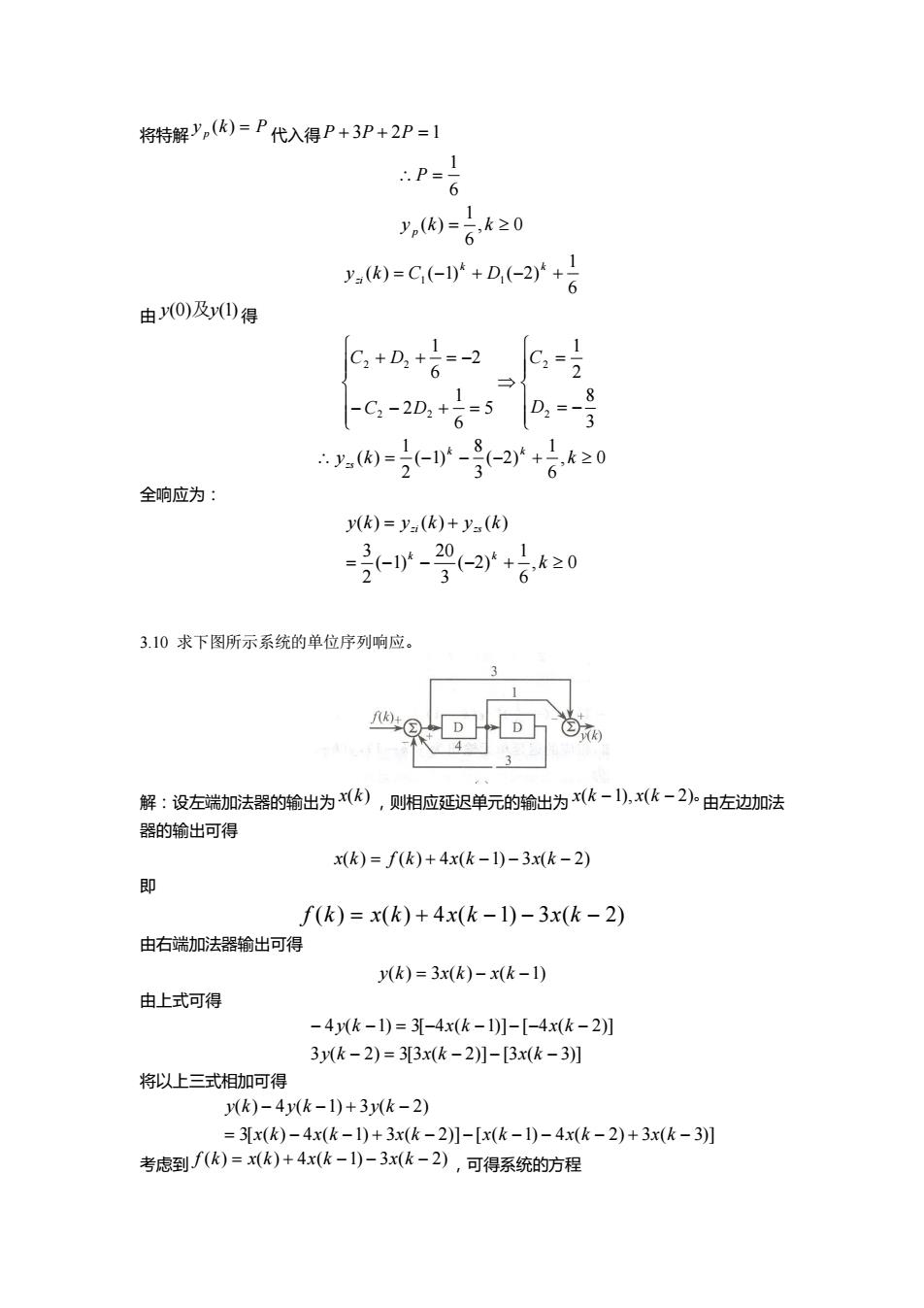
将特解 y p (k) P 代入得 P 3P 2P 1 , 0 6 1 ( ) 6 1 y k k P p 6 1 ( ) ( 1) ( 2) 1 1 k k yzi k C D 由 y(0)及y(1) 得 3 8 2 1 5 6 1 2 2 6 1 2 2 2 2 2 2 D C C D C D , 0 6 1 ( 2) 3 8 ( 1) 2 1 y (k) k k k zs 全响应为: , 0 6 1 ( 2) 3 20 ( 1) 2 3 ( ) ( ) ( ) k y k y k y k k k zi zs 3.10 求下图所示系统的单位序列响应。 解:设左端加法器的输出为 x(k) ,则相应延迟单元的输出为 x(k 1), x(k 2)。由左边加法 器的输出可得 x(k) f (k) 4x(k 1) 3x(k 2) 即 f (k ) x(k) 4x(k 1) 3x(k 2) 由右端加法器输出可得 y(k) 3x(k) x(k 1) 由上式可得 3 ( 2) 3[3 ( 2)] [3 ( 3)] 4 ( 1) 3[ 4 ( 1)] [ 4 ( 2)] y k x k x k y k x k x k 将以上三式相加可得 3[ ( ) 4 ( 1) 3 ( 2)] [ ( 1) 4 ( 2) 3 ( 3)] ( ) 4 ( 1) 3 ( 2) x k x k x k x k x k x k y k y k y k 考虑到 f (k) x(k) 4x(k 1) 3x(k 2) ,可得系统的方程

yk)-4k-)+3k-2)=3fk)-fk-1) 令右端只有(k)作用时,系统的单位序列响应为h,(k),它满足方程 h()-4h(k-1)+3h(k-2)=6k) 以及初始条件h(-)=(-2)=0则有 h(0)=4h,(-1)-3h,(-2)+6(0)=1 h(①)=61)+4h,(0)-3h(-1)=4 方程的解为h,(k)=C,+C23*,k≥0 将初始值代入,得 h(0)=C,+C=1 h)=C1+3C2=4 解以上两式可得9=~ 则系统的单位序列响应为 hk)=3h,(k)-h,(k-1)=【-1+43)1e(k) 3.11各序列的图形如图所示,求下列卷积和。 f(达 (d) (1)(k)*5(k) 原式=[6(k+1)+26(k)+6(k-1]*[ε(k+2)-ε(k-3) =6(k+3)+2(k+2)+6(k+I)-6(k-2)-(k-3)-s(k-4) =6…,0,13,4,4,4,31,0,} (2)()*f(附 原式=[ε(k+2)-s(k-3]*[36(k)+28(k-1)+8(k-2)] =(k+2)+2(k+)+5(k)-36(k-3)-2s(k-4)-6(k-5) .…0.3.56.6.63.1.0..1
y(k) 4y(k 1) 3y(k 2) 3 f (k) f (k 1) 令右端只有 (k) 作用时,系统的单位序列响应为 ( ) 1 h k ,它满足方程 ( ) 4 ( 1) 3 ( 2) ( ) 1 1 1 h k h k h k k 以及初始条件h1 (1) h(2) 0。则有 (1) (1) 4 (0) 3 ( 1) 4 (0) 4 ( 1) 3 ( 2) (0) 1 1 1 1 1 1 1 h h h h h h 方程的解为 h1 ( k ) C 1 C 2 3 , k 0 k 将初始值代入,得 (1) 3 4 (0) 1 1 1 2 1 1 2 h C C h C C 解以上两式可得 , 2 3 , 2 1 C1 C2 则有 3 ) ( ) 2 3 2 1 ( ) ( 1 h k k k 则系统的单位序列响应为 ( ) 3 ( ) ( 1) [ 1 4(3) ] ( ) 1 1 h k h k h k k k 3.11 各序列的图形如图所示,求下列卷积和。 (1) ( ) ( ) 1 2 f k f k ,0,1,3,4,4,4,3,1,0, ( 3) 2 ( 2) ( 1) ( 2) ( 3) ( 4) [ ( 1) 2 ( ) ( 1)]*[ ( 2) ( 3)] k k k k k k k k k k k 原式 (2) ( ) ( ) 3 4 f k f k { ,0,3,5,6,6,6,3,1,0 } ( 2) 2 ( 1) ( ) 3 ( 3) 2 ( 4) ( 5) [ ( 2) ( 3)]*[3 ( ) 2 ( 1) ( 2)] k k k k k k k k k k k 原式

3.12已知系统的激励)和单位序列响应)如下:求系统的零状态响应',() (2)f(K)=6(k),h(k)=6k)-6k-3) 解: y,()=f(k)*hk)=()*[6(k)-6k-3】 =£(k)-E(k-3) (4)f)=(0.5)'(k),hk)=()-(k-5) 解: y/()=fK)*hk)=(0.5)'ε(k)*[E(k)-E(k-5刃 =[∑(0.5)s(k)-∑0.5)s(k-5) =21-(0.5)]e(k)-21-(0.5)-6E(k-5) =[2-(0.5)*c(k)-2-(0.5)-5s(k-5) 322下图所示的复合系统由3个子系统组成,它们的单位序列响应分别为 h(k)=(k),h,()=(k-5)。求复合系统的单位序列响应。 →A肉 解令复合系统的单位序列响应为h(k),则有 h(k)=[h(k)-h(k)】*h(k)=[(k)-(k-5]*(k) 0,k<0 =k+10≤k≤4 5,k25
3.12 已知系统的激励 f (k) 和单位序列响应h(k) 如下:求系统的零状态响应 y (k) f 。 (2) f (k) (k),h(k) (k) (k 3) 解: ( ) ( 3) ( ) ( ) * ( ) ( ) *[ ( ) ( 3)] k k y k f k h k k k k f (4) f (k) (0.5) (k),h(k) (k) (k 5) k 解: [2 (0.5) ] ( ) [2 (0.5) ] ( 5) 2[1 (0.5) ] ( ) 2[1 (0.5) ] ( 5) [ (0.5) ] ( ) [ (0.5) ] ( 5) ( ) ( ) * ( ) (0.5) ( ) *[ ( ) ( 5)] 5 1 6 0 0 k k k k k k y k f k h k k k k k k k k k i k k i k k f 3.22 下 图 所 示 的 复 合 系 统 由 3 个 子 系 统 组 成 , 它 们 的 单 位 序 列 响 应 分 别 为 ( ) ( ), ( ) ( 5) h1 k k h2 k k 。求复合系统的单位序列响应。 解 令复合系统的单位序列响应为h(k) ,则有 5, 5 1,0 4 0, 0 ( ) [ ( ) ( )]* ( ) [ ( ) ( 5)]* ( ) 1 2 1 k k k k h k h k h k h k k k k