
一、选择题(每小题4分,共计20分) (以下题目均为单迷题,请得正确答案的标号(A或B或C或D或E) 填入题前的括号[]内) )1、信号f,(m)和f,(m)的波形如图所示,设f()=f,(m)*,(,则f(1)等 于 f1(k) f20) (a)1 (B)2 (C)0 D)-1 (E)3 ()2、计算6u-3)cos(m)d=? (A)1 (B)2 (C)0 (D)-1 (E)-2 〔)3、己知系统的输入为fm),输出为m),则系统m)=5fn-3)为: (A)非时变、 ®)时变、 (C)非时变、 ()时变、 因果系因果系统 因果系统 非因果系 统、 无记忆 记忆 记忆 统 无记忆 无记忆 〔)4、已知f()=26(t-3),则其拉普拉斯变换F(s)=? (A02e-2 (B)2e-3 (C)3e- (D)3e2 @)e 〔)5、序列差u(m)-(n-1)等于: (A)1 (B)6() (C)(n)(D)(n-l)(E)0 二、填空题(每小题4分,共计28分) 6、求傅立叶逆变换F-0e-】 = 1jo+21
一、 选择题(每小题 4 分,共计 20 分) (以下题目均为单选题,请将正确答案的标号(A 或 B 或 C 或 D 或 E) 填入题前的括号[ ]内) 〔 〕1、信号f1(n)和f2(n)的波形如图所示,设f(n)=f1(n)*f2(n),则f(1)等 于: k k f1(k) f2(k) 2 1 2 1 -1 0 1 -1 2 3 4 -1 0 1 2 3 (A)1 (B) 2 (C) 0 (D)-1 (E)3 〔 〕2、计算 − = ?)cos()3( ∫ +∞ ∞− δ π dttt (A)1 (B)2 (C)0 (D)-1 (E)-2 〔 〕3、已知系统的输入为 ,输出为 ,则系统 nf )( ny )( nfny −= )3(5)( 为: (A) 非时变、 因果系 统、 无记忆 (B)时变、 因果系统 无记忆 (C) 非时变、 因果系统 记忆 (D) 时变、 因果系统 记忆 (E) 时变、 非 因 果 系 统 无记忆 〔 〕4、已知 δ ttf −= ),3(2)( 则其拉普拉斯变换 sF = ?)( (A)2 s e−2 (B)2 s e−3 (C)3 s e−3 (D)3 s e−2 (E) s e s 1 −3 〔 〕5、序列差 nunu −− )1()( 等于: (A)1 (B)δ n)( (C) nu )( (D) nu − )1( (E) 0 二、填空题(每小题 4 分,共计 28 分) 6、 = ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ + − − 2 10 5 1 ω ω j e F j 求傅立叶逆变换 _______________
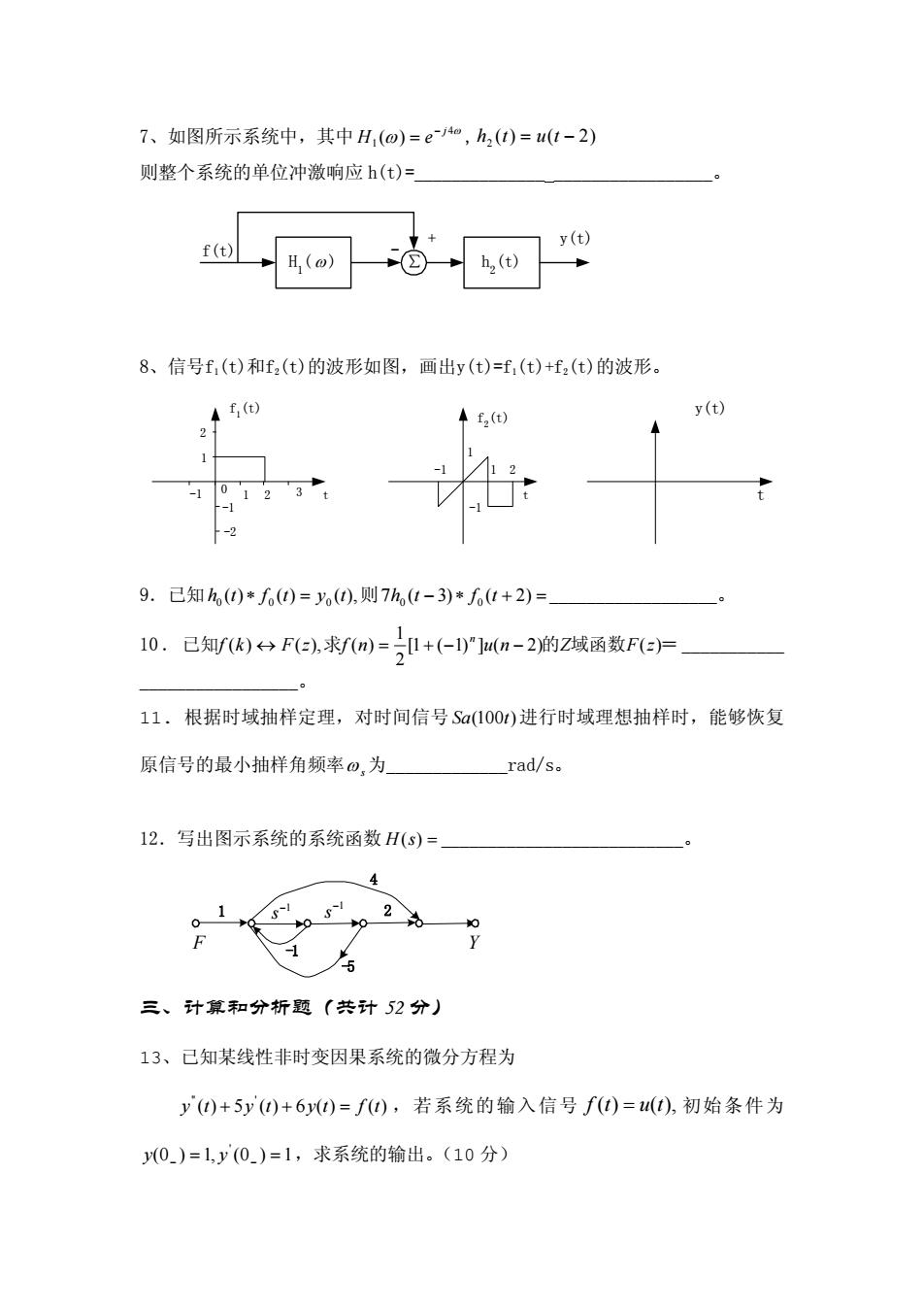
7、如图所示系统中,其中H,(@)=eo,h,()=ut-2) 测整个系统的单位冲激响应h(t)= f(t) H(o) 8、信号f,(t)和,(t)的波形如图,画出y(t)=f,(t)+f,(t)的波形。 4() y(t) 10123 -2 9.己知h,(0*f。0-0,则7h(1-3)*01+2)= 10.已知f()F(e),求f(m)=+(-)]un-2的Z域函数F(e)尸 11.根据时域抽样定理,对时间信号Sa(1001)进行时域理想抽样时,能够恢复 原信号的最小抽样角频率0,为 rad/s。 12.写出图示系统的系统函数H(s)= 4 三、计算和分析题(共计52分) 13、已知某线性非时变因果系统的微分方程为 y)+5y')+6)=f),若系统的输入信号f(t)=(0),初始条件为 0.)=1,y(0.)=1,求系统的输出。(10分)
7、如图所示系统中,其中 ,ω ω 4 1 )( j eH − = )2()( 2 = tuth − 则整个系统的单位冲激响应 h(t)=______________ _________________。 H1 ( ) ∑ h2(t) y(t) f(t) + - ω 8、信号f1(t)和f2(t)的波形如图,画出y(t)=f1(t)+f2(t)的波形。 0 -1 1 2 1 2 -1 -2 t f1(t) 3 y(t) t t f2 (t) -1 21 1 -1 9.已知 0 0 =∗ 0 tytfth ),()()( 则 0 − ∗ 0 tfth + )2()3(7 = __________________。 10.已知 求 )2(])1(1[ 的 域函数 )( = 2 1 nfzFkf )(),()( zFZnu n ↔ −−+= ___________ _________________。 11.根据时域抽样定理,对时间信号 进行时域理想抽样时,能够恢复 原信号的最小抽样角频率 tSa )100( ω s为_____________rad/s。 12.写出图示系统的系统函数 sH )( = __________________________。 1 −1 s −1 s 2 4 -5 -1 F Y 三、计算和分析题(共计 52 分) 13、已知某线性非时变因果系统的微分方程为 " ' =++ tftytyty )()(6)(5)( ,若系统的输入信号 = tutf ),()( 初始条件为 − yy ' − == 1)0(,1)0( ,求系统的输出。(10 分)
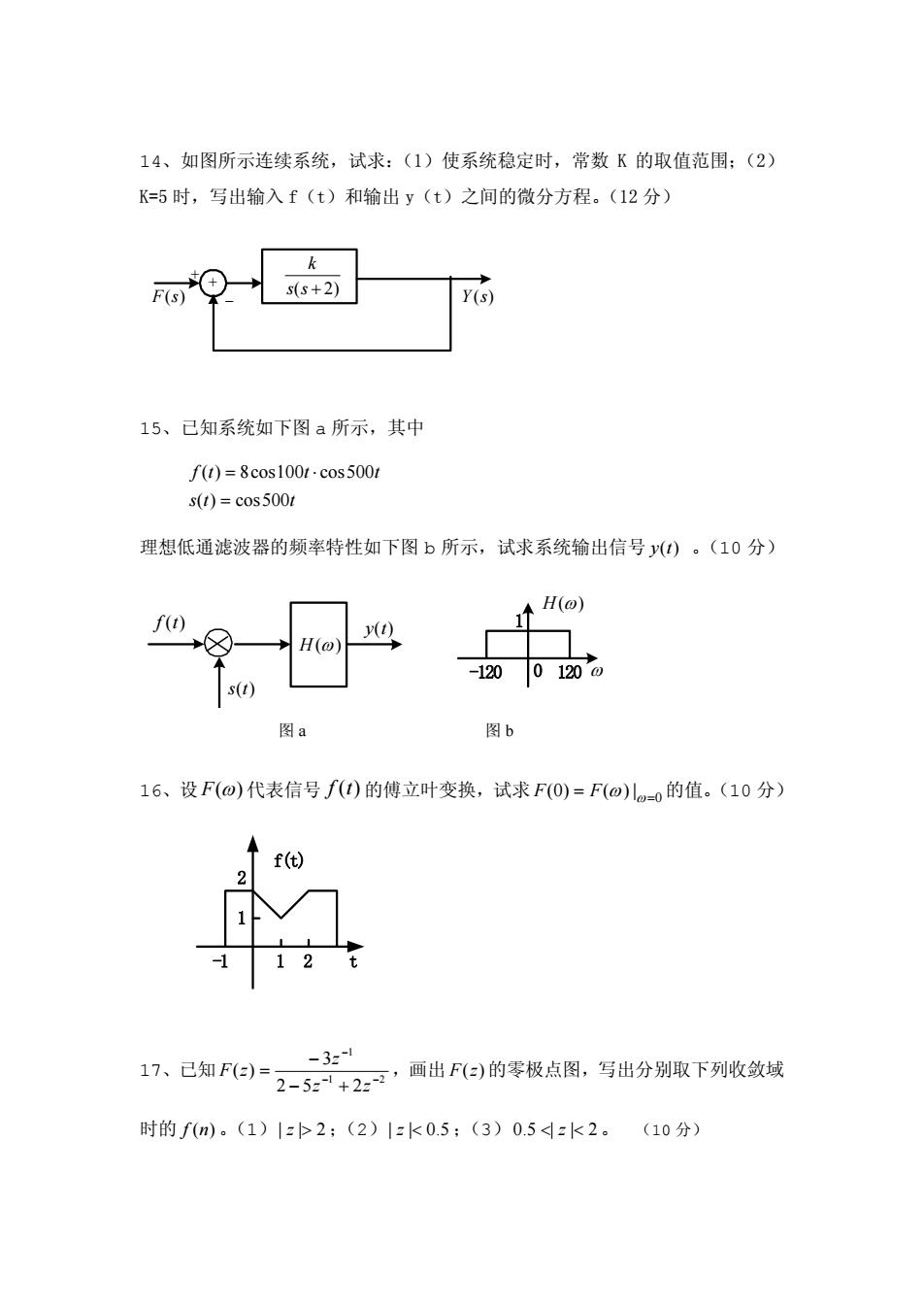
14、如图所示连续系统,试求:(1)使系统稳定时,常数K的取值范围:(2) K=5时,写出输入f(t)和输出y(t)之间的微分方程。(12分) F(s) s(5+2) 15、已知系统如下图a所示,其中 f(r)=8cos100t-cos500r s()=cos5001 理想低通滤波器的频率特性如下图b所示,试求系统输出信号()。(10分) H(o) f() H(@) -1200120'o s(1) 图a 图b 16、设F(@)代表信号f(I)的傅立叶变换,试求F(O)=F(o)lm0的值。(10分) f(t) 12 17、己知F(e) 2-。+2:,面出阳)的零极点图,写出分别取下列收致线 -321 时的fm)。(1)1=2(2)1=k0.5:(3)0.5=k2。(10分)
14、如图所示连续系统,试求:(1)使系统稳定时,常数 K 的取值范围;(2) K=5 时,写出输入 f(t)和输出 y(t)之间的微分方程。(12 分) + sF )( sY )( ss + )2( k + - 15、已知系统如下图 a 所示,其中 tts tf tt 500cos)( 500cos100cos8)( = ⋅= 理想低通滤波器的频率特性如下图 b 所示,试求系统输出信号 ty )( 。(10 分) -120 0 1 ty )( H ω)( tf )( H ω)( 120 ω ts )( 图 a 图 b 16、设 F ω)( 代表信号 的傅立叶变换,试求 tf )( 0 |)()0( = = ω ω FF 的值。(10 分) -1 1 2 t 1 2 f(t) 17、已知 1 2 1 252 3 )( − − − +− − = zz z zF ,画出 的零极点图,写出分别取下列收敛域 时的 。(1) ;(2) zF )( nf )( z > 2|| z < 5.0|| ;(3) < z < 2||5.0 。 (10 分)