
一、选择题(每小题4分,共计20分) (以下题目均为单选题,请将正确答的标号(月或B或C或D或E) 填入题前的括号[]内) ()1.卷积(u+1)*(t-1)的结果为: (B) (C) (D) (1+1)s(t+l)(1-1)s(t-) 1E(1) (t+1)s(1-1) ()2.离散系统k)=(k)属于: ()记忆、时不变 ⑧)无记忆、时 线性、非因果、不稳变,非线性、因果、 足 稳定 不稳定 不稳定 ()3.序列差(k)-(k-1)等于: ()1 B)6k) (C)s(k) D)s(K-1) ()4.已知f0分FU@),求f(31-2)的傅里叶变换: (A) (C) 3F(Bo)e ()5.已知f)=261-3),则其拉普拉斯变换F(s)=? ω1e(⑧)2e2 (C2e3 (D)3e2 二、填空题(每小题4分,共计28分) 6.信号f)=cos31+sin41的周期为: 7.f(t)=[e6()dr= 8.从信号频谱的连续性和离散性来考虑,周期信号的频谱是 9.已知f)→F(),求f)=k-1)k-2)对应的Z域函数: F(Z)= 10.设f)是一有限频宽信号,频带宽度为BHz
一、 选择题(每小题 4 分,共计 20 分) (以下题目均为单选题,请将正确答案的标号(A 或 B 或 C 或 D 或 E) 填入题前的括号[ ]内) ( )1.卷积ε + ε tt − )1(*)1( 的结果为: (A) ε tt ++ )1()1( (B) ε tt −− )1()1( (C) ε tt )( (D) + ε tt − )1()1( ( )2.离散系统 = kkfky )()( 属于: (A)记忆、时不变、 线性、非因果、不稳 定 (B) 无记忆、时 变、非线性、因果、 稳定 (C)记忆、时不 变、线性、因果、 不稳定 (D) 无记忆、时 变、线性、因果、 不稳定 ( )3.序列差ε ε kk −− )1()( 等于: (A) 1 (B) δ k)( (C) ε k)( (D) ε k − )1( ( )4.已知 ↔ jFtf ω)()( ,求 tf − )23( 的傅里叶变换: (A) ω ω 3 2 )3(3 j ejF − (B) ω ω 3 2 ) 3 ( 3 1 j ejF − (C) ω ω 3 2 ) 3 ( 3 1 j ejF (D) ω ω 2 3 ) 2 ( 2 1 j ejF − ( )5.已知 δ ttf −= ),3(2)( 则其拉普拉斯变换 sF = ?)( (A) s e s 1 −3 (B) 2 s e −2 (C) 2 s e−3 (D) 3 s e−2 二、填空题(每小题 4 分,共计 28 分) 6.信号 += 4sin3cos)( tttf 的周期为: 7. () ) ′ = ∫ f = e δ ( τ ∞− − t τ t d 3τ 8.从信号频谱的连续性和离散性来考虑,周期信号的频谱是 9.已知 ↔ kkkfzFkf −−= )2()1()(),()( 对应的 Z 域函数: k 求 ε F(Z)= _______________ 10.设 f(t)是一有限频宽信号,频带宽度为 B Hz
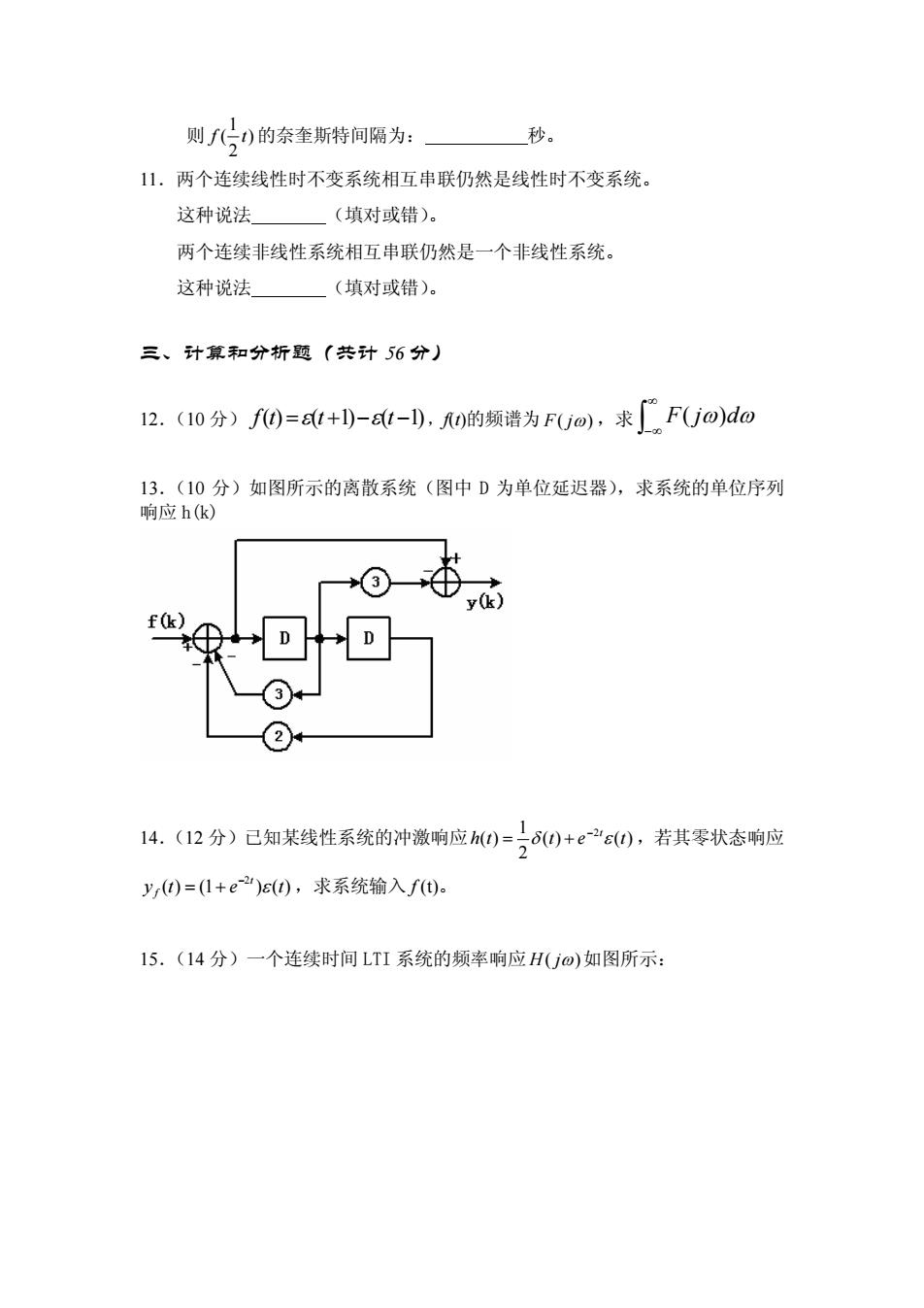
则f八)的奈奎斯特间隔为:—秒。 11.两个连续线性时不变系统相互串联仍然是线性时不变系统。 这种说法 (填对或错)。 两个连续非线性系统相互串联仍然是一个非线性系统。 这种说法 一(填对或错)。 三、计算和分析题(共计56分) 12.(10分)f0=+)--),0的频谱为FUo),求FUo)do 13.(10分)如图所示的离散系统(图中D为单位延迟器),求系统的单位序列 响应hk) ③ f(k) (② 14.(12分)已知某线性系统的冲激响应h)=,)+eε),若其零状态响应 y)=(1+e)e(),求系统输入f()。 15.(14分)一个连续时间LTI系统的频率响应H(Uo)如图所示
则 ) 2 1 ( tf 的奈奎斯特间隔为: 秒。 11.两个连续线性时不变系统相互串联仍然是线性时不变系统。 这种说法 (填对或错)。 两个连续非线性系统相互串联仍然是一个非线性系统。 这种说法 (填对或错)。 三、计算和分析题(共计 56 分) 12.(10 分) ε −+= ε tttf − )1()1()( ,f(t)的频谱为 jF ω)( ,求 ∫ ∞ ∞− )( djF ωω 13.(10 分)如图所示的离散系统(图中 D 为单位延迟器),求系统的单位序列 响应 h(k) 14.(12 分)已知某线性系统的冲激响应 )()( 2 1 )( 2 tetth t εδ − += ,若其零状态响应 f += −2t ε tety )()1()( ,求系统输入 f (t)。 15.(14 分)一个连续时间 LTI 系统的频率响应 jH ω)( 如图所示:

H(jo) 1 -15oo15oo -300-2.500 0 2.500300 00 (1)输入f)=2cos(o,)-3sin(2o,),求输出y(t); (2)是否存在其他的周期性输入信号(①),其奇波频率为,使其经过该系统 后输出等于(1)中的和?如果有,请给出)的表达式,如果没有,请说明 原因。 16(0分已米连维桐系装的系货酒黄州的二。检 出该系统的状态方程
jH ω)( 2 (1)输入 )2sin(3)cos(2)( 0 0 tf = ω t − ω t ,求输出 y(t); (2)是否存在其他的周期性输入信号f1(t),其奇波频率为ω0,使其经过该系统 后输出等于(1)中的 f(t) ?如果有,请给出f1(t)的表达式,如果没有,请说明 原因。 16.(10 分)已知某连续时间系统的系统函数为: 。试给 出该系统的状态方程。 -2.5ω0 0 -1.5ω0 1 1.5ω0 -3ω0 2.5ω0 3ω0 ω