
Chapter 5 2 Chapter 5 Stability Analysis Objectives: Input-output stability 。Internal stability ·Lyapunov theorem rol Theory Stability analysis of LTI systems
Chapter 5 Stability Analysis Objectives: • Input-output stability • Internal stability • Lyapunov theorem • Stability analysis of LTI systems Chapter 5 2
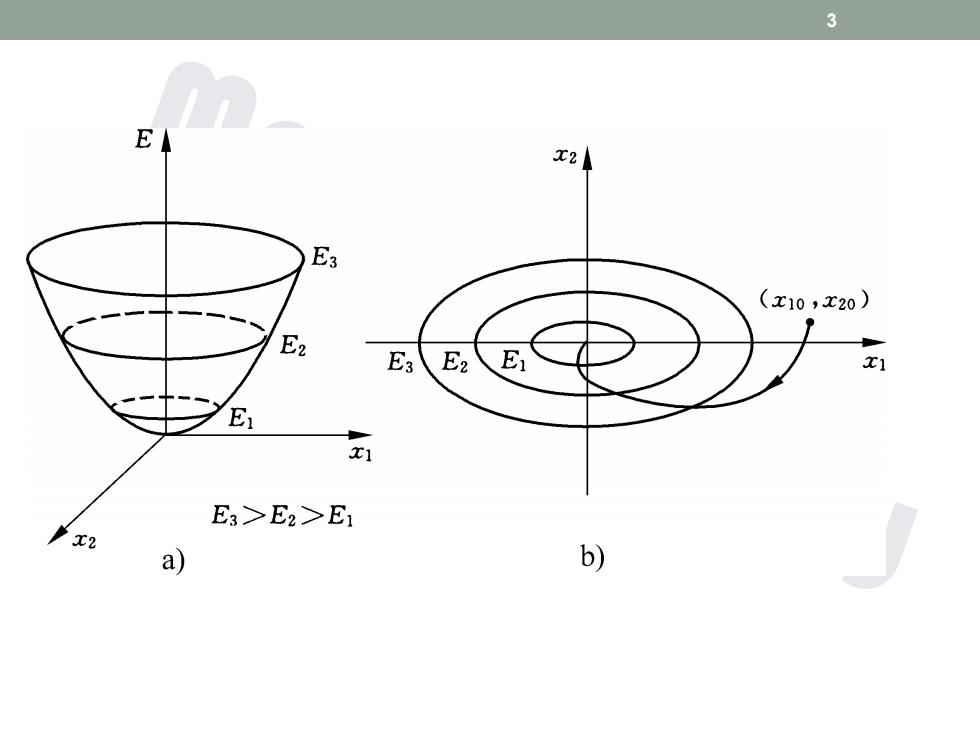
3 E X2 E3 (x10,x20) E2 E3 E2 E x1 E x1 E3>E2>E1 'x2 a) b)
3
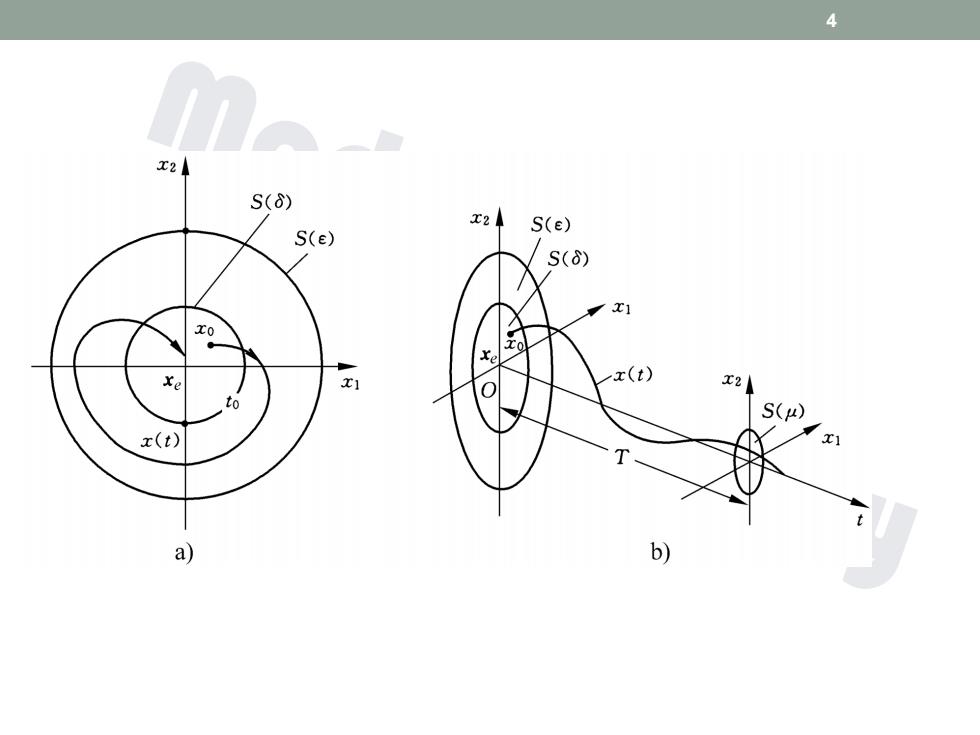
4 S(8) x2 S(e) S(e) S(6) xe x(t) S(μ) z(t) a) b)
4

Chapter 5 5 5.1 Input-output stability An input u(t)is bounded if there exists a constant um: u(t)≤um<oo A system said to be BlBO(bounded input bounded output)if for every bounded input excites a bounded output.The definition is for zero-state response condition or initially relax systems. Theorem:A SISO is BIBO if and only if the pulse response g()is:lg(tdt≤M<o
5.1 Input-output stability • An input u(t) is bounded if there exists a constant um: • A system said to be BIBO (bounded input bounded output) if for every bounded input excites a bounded output. The definition is for zero-state response condition or initially relax systems. • Theorem: A SISO is BIBO if and only if the pulse response g(t) is : 5 u(t ) um g( t )dt M 0 Chapter 5

Chapter 5 6 Proof: If input u is bounded,then< =fst-ww()de ≤lgt-列lur小t=ulst- flgt-dr≤M<o ly≤umM=K2 Therefore,output y is bounded,i.e.K<
Proof: • If input u is bounded, then • Therefore, output y is bounded, i.e. 6 g(t τ) u(τ ) dτ u g(t τ) dτ y g(t τ)u(τ )dτ t t m t t t t 0 0 0 If g(t τ) d τ M t t 0 u M K2 y m u um y K2 Chapter 5

Chapter 5 7 Example: A linear system as follows,where a is a positive constant, impulse response is g)=ce.Determine the stability of the following system. 文=-X+W wie-d Solution: So the system is BIBO stable
• Example: • A linear system as follows, where a is a positive constant, impulse response is . Determine the stability of the following system. • Solution: • So the system is BIBO stable. 7 y cx x ax u at g( t ) c e 0 0 1 0 0 a a a c g( τ ) d τ c e d τ aτ Chapter 5

Chapter 5 Theorem:A SISO system with proper rational transfer function G(s)is BIBO,if and only if the every pole of G(s) has negative real part,or lies inside left-half s-plane. (From classical control theory) ● 。 Theorem:A multi-variable system is BIBO if and only if every pole of transfer function matrix G(s)=[g(s)]has negative real part or lies inside left-half s-plane
• Theorem: A SISO system with proper rational transfer function G(s) is BIBO, if and only if the every pole of G(s) has negative real part, or lies inside left-half s-plane. (From classical control theory) • Theorem: A multi-variable system is BIBO if and only if every pole of transfer function matrix G(s)=[gij(s)] has negative real part or lies inside left-half s-plane. • Chapter 5 8

Chapter 5 9 Discrete system: Theorem:A SISO discrete system is BIBO if and only if g(k)is absolutely summable in [0,+o): ∑g(ksM<∞ 0 Theorem:A SISO discrete system is BIBO if and only if every pole of G(z)has a magnitude less than 1. Theorem:A multi-variable discrete system is BIBO if and only if every pole of matrix G(z)=[gi(z)]has a magnitude less than 1
Discrete system: • Theorem: A SISO discrete system is BIBO if and only if g(k) is absolutely summable in [0, +): • Theorem: A SISO discrete system is BIBO if and only if every pole of G(z) has a magnitude less than 1. • Theorem: A multi-variable discrete system is BIBO if and only if every pole of matrix G(z)=[gij(z)] has a magnitude less than 1. 9 g( k ) M 0 Chapter 5

Chapter 5 10 5.2 Internal stability The BIBO stability is defined for the zero-state response. Stability of zero-input response is defined as internal 。 stability. For zero-input case,system model and solution: 文=Ax x=eMxo "heory Therefore,the bound of x is determined by A
5.2 Internal stability • The BIBO stability is defined for the zero-state response. • Stability of zero-input response is defined as internal stability. • For zero-input case, system model and solution: • Therefore, the bound of x is determined by A. 10 0 x e x x Ax At Chapter 5

Chapter 5 11 Continuous system Theorem:The equation =x is marginally stable if and only if all eigenvalues of A have zero or negative real parts and those with zero real parts are simple roots of the minimal polynomial of A. Theorem:The equation=x is asymptotically stable if and only if all eigenvalues of A have negative real parts. Definition:A is stable if every eigenvalues of A has negative real part
Continuous system • Theorem: The equation is marginally stable if and only if all eigenvalues of A have zero or negative real parts and those with zero real parts are simple roots of the minimal polynomial of A. • Theorem: The equation is asymptotically stable if and only if all eigenvalues of A have negative real parts. • Definition: A is stable if every eigenvalues of A has negative real part. 11 x Ax x Ax Chapter 5