上海交通大学：《现代控制理论》课程教学资源（讲稿）Chapter 6 Controllability and Observability

Chapter 6 2 Chapter 6 Controllability and Observability Objectives: Definition of controllability Definition of observability Detective methods for controllability I Theory Detective methods for observability ·Decomposition

Chapter 6 Controllability and Observability Objectives: • Definition of controllability • Definition of observability • Detective methods for controllability • Detective methods for observability • Decomposition Chapter 6 2

Chapter 6 3 6.1 controllability 。Definition: The state equation=x+Bu or the pair (A,B)is said to be controllable if for any initial state x(O)=xo and any final state x1,there exists an input that transfer xo to x1 in a finite time.Otherwise is said to be uncontrollable Theory

6.1 controllability • Definition: • The state equation or the pair (A,B) is said to be controllable if for any initial state x(0)=x0 and any final state x1 , there exists an input that transfer x0 to x1 in a finite time. Otherwise is said to be uncontrollable. 3 x   Ax  Bu Chapter 6

Chapter 6 4 Example:uncontrollable network. 10k2 Let x=uc,x2 =uc2 33μF 10k2 4C2 33uF y=Cx=0 1 f0n-日henx0-erdi→xE起 No matter what the input is,the states are always equivalent. So the states of the system are uncontrollable

Example: uncontrollable network. 4 y Cx  x x Ax bu x u x uc , x uc 0 1 1 1 1 2 2 1 Let 1 1 2 2                                           t t t t t t t t t 3 3 3 3 e e e e e e e e 2 1 e A        0 0 If then x(0) x t u τ τ t t τ e ( )d 1 1 ( ) 0 ( )           x1  x2 No matter what the input is, the states are always equivalent. So the states of the system are uncontrollable. Chapter 6

Chapter 6 5 Theorem:The following statements are equivalent. 1.The n-dimensional pair(A,B)is controllable. 2. The following nxn matrix is non-singular for any t. W0-eBBte de-BBed 3. The following nxnp controllability matrix(Kalman matrix) has rank n(full row rank). C=BAB…A"B]

• Theorem: The following statements are equivalent. 1. The n-dimensional pair (A,B) is controllable. 2. The following nn matrix is non-singular for any t. 3. The following nnp controllability matrix (Kalman matrix) has rank n (full row rank). 5 W (t) e BB e dτ e BB e dτ A(t-τ ) T A (t τ) t Aτ T A τ t C T T          0 0 ] 1 C B AB A B  n-  [ Chapter 6

Chapter 6 A system is controllable if the following nxnp controllability matrix has rank n(full row rank). Oc=[B AB A'B·Am-B] rank Oc =n Proof:Caley-Hamilton theorem e*-d()I+a()4+>Fa.i()A->a() →x0)=-∑ABa,(ra(r)dr Ba neory i=0 a(r)u(r)dr- B2 =B(i=0,1,…,n-1) Br

A system is controllable if the following nnp controllability matrix has rank n (full row rank). Q [B AB A B A B] 2 n 1 C    rank QC  n Proof: Caley-Hamilton theorem           1 0 1 0 1 1 ( ) ( ) ( ) ( ) n i i i n- n τ e a τ I a τ A a τ A a τ A A  x a τ τ τ t i n i i (0) ( ) ( )d 1 0 1 0 A B u       i ir i i t i β β β a τ τ τ                  2 1 0 ( ) ( )d 1 u (i  0,1,  ,n 1) Chapter 6

Chapter 6 7 Bo Therefore x(0)=-[B AB A"B B The solution of B exists according to initial state x(0)only if following matrix has rank n. rank2c=rank[B7AB。AB A"-B]=n Theory

7 Therefore               1 1 0 1 (0) [ ] n n- β β β x B AB A B     n  rank Q rank[B AB A B A B] 2 n 1 C  The solution of  exists according to initial state x(0) only if following matrix has rank n. Chapter 6

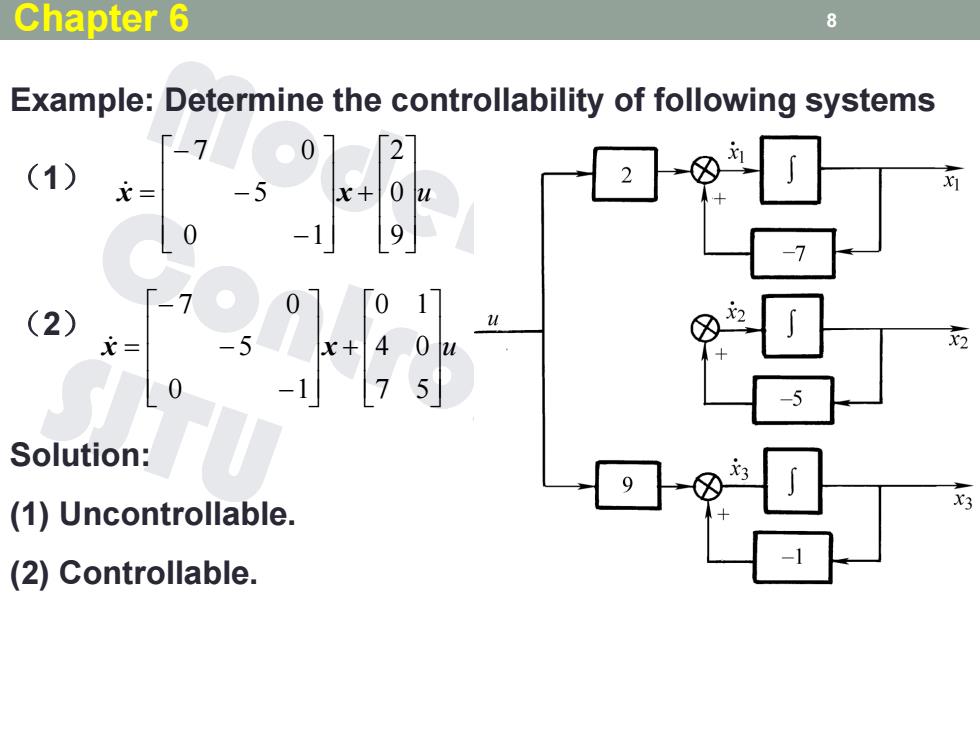
Chapter 6 8 Example:Determine the controllability of following systems 「-7 ●0 2 (1) = 0 2 9 -7 (2) Solution: 9 (1)Uncontrollable. (2)Controllable

8 Example: Determine the controllability of following systems u                          9 0 2 0 1 5 7 0 x x u                          7 5 4 0 0 1 0 1 5 7 0 x x （1） （2） Solution: (1) Uncontrollable. (2) Controllable. Chapter 6

Chapter 6 9 Example:Determine the controllability of following systems -4.1 0 「0 (1) = 0 -4 0 X十 u 0 0 -2 3 -4 0 4 2 0 -4 0 x+ 0 -2 3 。Solution: Theory ·(1)Controllable. ·(2)Uncontrollable

• Example: Determine the controllability of following systems • (1) • (2) 9 u                          3 4 0 0 0 2 0 4 0 4 1 0 x x u                          3 0 0 0 4 2 0 0 2 0 4 0 4 1 0 x x • Solution: • (1) Controllable. • (2) Uncontrollable. Chapter 6

Chapter 6 10 Theorem:If all the eigenvalues of a system are different,then the system can be transformed to the following form using similarity transformation.The system is controllable if there is no all zero row in B. 0 heory

10 Theorem: If all the eigenvalues of a system are different, then the system can be transformed to the following form using similarity transformation. The system is controllable if there is no all zero row in . x x  Bu              n λ λ λ 0 0 2 1   B Chapter 6

Chapter 6 11 Other conditions of controllability Theorem:If a system can be transformed to the following Jordan matrix form using similarity transformation.It is controllable if each row in matrix B corresponding to the last rows of each Jordan block is not all zero row. x+Bu J=

Other conditions of controllability 11 Theorem: If a system can be transformed to the following Jordan matrix form using similarity transformation. It is controllable if each row in matrix corresponding to the last rows of each Jordan block is not all zero row. B Chapter 6 x Bu J J J x               0 k 0 2 1                i i i i λ λ λ 0 1 1 0   J