
4.6求下列周期信号的基波角频率和周期T。 (4)cos(2)+cos(3)+cos(5) 牌:角期为0=0:,7-合-2 oo号0+o写0+cof0 解:角率为D-01ad: 周期 4.7用直接计算傅立叶系数的方法,求图示周期函数的傅立叶系数(三角形式和指数形式)。 (a) (b) (1)(1)图a: 行2,则有 1,4k-1≤1≤4k+1 f0=0.4k+1≤1≤4k+3 由此可得 a-退0eoh=0ca受h =0cod=2。 mn=02 b,=号f0 sin(nOr)dr=f0smd =上sm”ah=0n=12… F,=- nπ ,n=0,t1,+2 (2)(2)图b: 解:周期T=2 ,则有 sin(m),2ks1≤2k+1 f)= 0,2k+1<1<2k+2 由此可得
4.6 求下列周期信号的基波角频率和周期 T。 (4)cos(2t) cos(3t) cos(5t) 解:角频率为 rad /s ,周期 T 2s 2 (6) t) 5 t) cos( 3 t) cos( 2 cos( 解:角频率为 rad / s 30 ,周期 T 60s 2 4.7 用直接计算傅立叶系数的方法,求图示周期函数的傅立叶系数(三角形式和指数形式)。 (1) (1) 图 a: 解:周期 T=4, 2 2 T ,则有 0,4 1 4 3 1,4 1 4 1 ( ) k t k k t k f t 由此可得 , 0, 1, 2 ) 2 sin( 0, 1,2 2 sin 2 1 ) 2 ( )sin( 2 1 ( )sin( ) 2 sin( ), 0,1,2 2 ) 2 ( ) cos( 2 1 ) 2 ( ) cos( 2 1 ( ) cos( ) 2 1 1 2 2 2 2 1 1 2 2 2 2 n n n F dt n n t dt n t f t n t dt f t T b n n n n dt n t f t dt n t f t n t dt f t T a n T n T T n T (2) (2) 图 b: 解:周期 T=2, T 2 ,则有 0,2 1 2 2 sin( ),2 2 1 ( ) k t k t k t k f t 由此可得
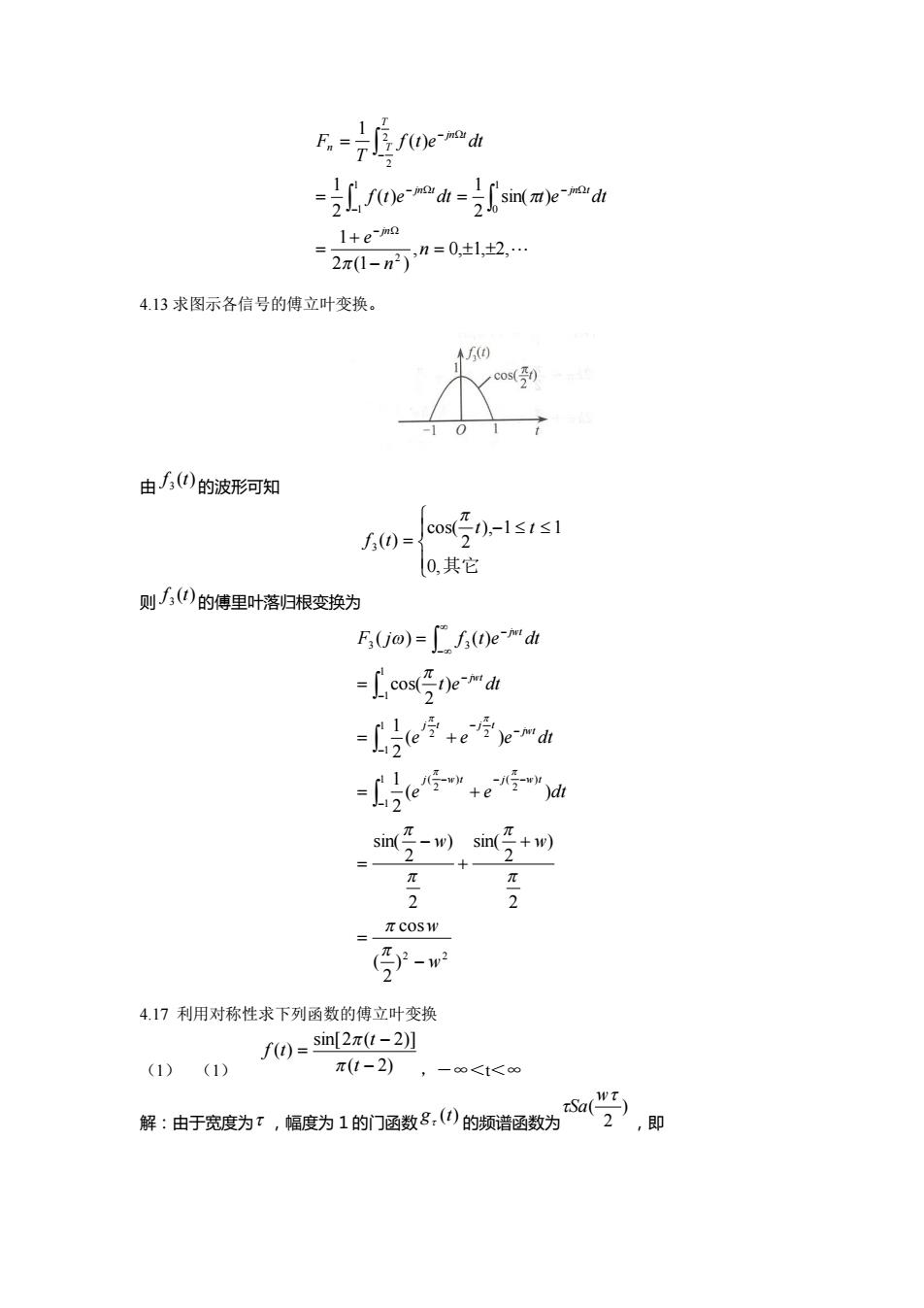
F.(ed Lefsirae 2a0-mn=0l2 4.13求图示各信号的傅立叶变换。 由/)的波形河知 f0)= cos-1s1≤1 0,其它 则/()的傅里叶落归根变换为 FUo)=广f0)ed -fcose-mdi -Ltyemdr (t sin-v)sinw) (孕-w 4.17利用对称性求下列函数的傅立叶变换 f0)=sim2π1-21 (1)(1) π(1-2) -o<1< 样:由于宽动:,低童为1的门面品,0的抚数为受,即
, 0, 1, 2, 2 (1 ) 1 sin( ) 2 1 ( ) 2 1 ( ) 1 2 1 0 1 1 2 2 n n e f t e dt t e dt f t e dt T F jn jn t jn t T T jn t n 4.13 求图示各信号的傅立叶变换。 由 ( ) 3 f t 的波形可知 0,其它 ), 1 1 2 cos( ( ) 3 t t f t 则 ( ) 3 f t 的傅里叶落归根变换为 2 2 1 1 ) 2 ) ( 2 ( 1 1 2 2 1 1 3 3 ) 2 ( cos 2 ) 2 sin( 2 ) 2 sin( ( ) 2 1 ( ) 2 1 ) 2 cos( ( ) ( ) w w w w e e dt e e e dt t e dt F j f t e dt j w t j w t jwt j t j t jwt jwt 4.17 利用对称性求下列函数的傅立叶变换 (1) (1) ( 2) sin[2 ( 2)] ( ) t t f t ,-∞<t<∞ 解:由于宽度为 ,幅度为 1 的门函数 g (t) 的频谱函数为 ) 2 ( w Sa ,即

.0 取π=2,幅度为2,根据傅里叶变换线性性质有 Fr8:01=)×2aw)=5aw0 即28,0Sa(m 注意到8,0是偶函数,根据对称性可得 Sa02r×782(w)=g,(w) 根据时移性和尺度变换性可知 FSa2r-2训=8.wen 由m四02别-2v-3 π(1-2) 可知 F (ees2madls 0,w 2xrad/s 2a 2)0=a4n∞<1<m 解· e 2a a2+p2 w2e+叫=2州 2a 2a 即0=0<1< 的傅里叶变换为2e州 4,18求下列信号的傅立叶变换 (2)f0=e--"8'u-l) 解:f0=e-8'-)=6-)-(-3)6t-1)=6'u-+360- 又8)分1,8'()分",由时移特性可知/的傅里叶变换为 F(w)=(w+3)e-m 4.20若已知0,试求下列函数的频谱: (8)ef3-2) 由尺度变换特性和时移特性可得
2 ) 2 sin( ) 2 ( ) ( w w w g t Sa 取 2,幅度为 2 1 ,根据傅里叶变换线性性质有 2 ( ) ( ) 2 1 ( )] 2 1 [ F g2 t Sa w Sa w 即 ( ) ( ) 2 1 g2 t Sa w 注意到 ( ) 2 g t 是偶函数,根据对称性可得 ( ) ( ) 2 1 ( ) 2 Sa t g2 w g2 w 根据时移性和尺度变换性可知 j w F Sa t g w e 2 4 ( ) 2 1 [ [2 ( 2)] 由 2 [2 ( 2)] ( 2) sin[2 ( 2)] ( ) Sa t t t f t 可知 w rad s e w rad s F f t g w e j w j w 0, 2 / , 2 / ( ) 2 1 [ ( )] 2 2 4 (2) t a t a f t , 2 ( ) 2 2 解: 由于 2 2 2 a w a e a t a w a w e e a w a 2 2 2 2 2 即 t a t a f t , 2 ( ) 2 2 的傅里叶变换为 a w e 2 4.18 求下列信号的傅立叶变换 (2) ( ) '( 1) 3( 1) f t e t t 解: ( ) '( 1) '( 1) ( 3) ( 1) '( 1) 3 ( 1) 3( 1) f t e t t t t t t 又 (t) 1, '(t) jw,由时移特性可知 f (t) 的傅里叶变换为 jw F jw jw e ( ) ( 3) 4.20 若已知[],试求下列函数的频谱: (8)e f (3 2t) jt 由尺度变换特性和时移特性可得

-20F-党 B-20片r-学 又由频移特性可得 6-2eg学fU5与当 FU/G-2F d*」 (9)di xt 解:由时域微分特性可得 又有 a分-jgn(W) 则由时域卷积定理可得 即层=m 4.34某LT系统的频率响应 若系统输入f0)=c0s2)),求该系统的输出0 解:系统输入的傅里叶变换为 F(r)=Fc0s2t=πδ(P+2)+ǒ(1w-2)l 则系统输出的傅里叶变换为 Y(w)=F()H()=6(w+2)+8(w-2 =jπ[8(w+2)-6(-2] 其傅里叶变换为 y(t)=F[Y(w)]=sin(2t) 此即为系统输入为/(0=c0s(2)时系统的输出
) 2 ( 2 1 (3 2 ) ) 2 ( 2 1 ( 2 ) 2 3 w f t e F j w f t F j w j 又由频移特性可得 ) 2 1 ( 2 1 [ (3 2 ) ] ) 2 1 ( 2 1 (3 2 ) 2 3( 1) 2 3( 1) w F f t e e F j w f t e e F j w j jt w j jt (9) dt t df t 1 * ( ) 解:由时域微分特性可得 f (t) jwF ( jw) dt d 又有 sgn( ) 1 j w t 则由时域卷积定理可得 ( ) ( )sgn( ) 1 ( ) * jwF jw j w t f t dt d 即 ] ( ) 1 [ ( ) * w F jw t f t dt d F 4.34 某 LTI 系统的频率响应 jw jw H jw 2 2 ( ) 若系统输入 f (t) cos(2t) ,求该系统的输出 y(t) 解:系统输入的傅里叶变换为 F( jw) F[cos2t] [ (w 2) (w 2)] 则系统输出的傅里叶变换为 [ ( 2) ( 2)] 2 2 ( ) ( ) ( ) [ ( 2) ( 2)] j w w jw jw Y jw F jw H jw w w 其傅里叶变换为 y(t) F[Y( jw)] sin(2t) 此即为系统输入为 f (t) cos(2t) 时系统的输出

-6rad/s< 片,0<w<6rad1s 0,其它 4.36一个LT1系统的频率响应 种人0-o天他 解:幅度为2'宽度为2的窗函数的博里叶变换为S(w),即有 28,)Sap) 由对称性可得 s30g。m) 又有cos(5)分π[8(w+5)+(w-5 则由频域卷积定理可得 F(w)=Frin30.cos(5】 1 F2元gw)*x[6(w+5)+6w-5 =g,0w+5+80m-5刃 又由已知可得 [j,-6rad/s<w<0 H(jw)=-j,0<w<6rad/s 0,其它 则系统输出的傅里叶变换为 Y()=F(hr)H()-L/g.(w+4)-Jg.(-) =8.0m)*j60w+4)-60w-4圳 =2元e,(*j6w+)-6w-4 又由傅里叶变换对称性可得 F1sin(4】=jπ[8(w+4)-8(w-4月 则由频域卷积定理可得系统的输出为 ()FLY()sin(2 sin(4r) t
4.36 一个 LTI 系统的频率响应 0,其它 ,0 6 / , 6 / 0 ( ) 2 2 e w rad s e rad s w H jw j j 若输入 cos(5 ), sin(3 ) ( ) t t t f t 求该系统的输出 y(t)。 解:幅度为 , 2 1 宽度为 2 的窗函数的傅里叶变换为Sa(w) ,即有 ( ) ( ) 2 1 g2 t Sa w 由对称性可得 ( ) sin(3 ) g6 w t t 又有 cos(5t) [ (w 5) (w 5)] 则由频域卷积定理可得 [ ( 5) ( 5)] 2 { ( ) * [ ( 5) ( 5)]} 2 1 ]* [cos( 5 )] sin( 3 ) [ 2 1 cos( 5 )] sin( 3 ) ( ) [ 6 6 6 g w g w g w w w F t t t F t t t F jw F 又由已知可得 0,其它 ,0 6 / , 6 / 0 ( ) j w rad s j rad s w H jw 则系统输出的傅里叶变换为 { ( ) * [ ( 4) ( 4)]} 2 1 ( ) * [ ( 4) ( 4)] 2 1 [ ( 4) ( 4)] 2 ( ) ( ) ( ) 4 4 4 4 g w j w w g w j w w Y jw F jw H jw jg w jg w 又由傅里叶变换对称性可得 F[sin(4t)] j[ (w 4) (w 4)] 则由频域卷积定理可得系统的输出为 sin(4 ) sin(2 ) ( ) [ ( )] t t t y t F Y jw

4.48有限频带信号(0)的最高频率为100出,若对下列信号进行时域取样,求最小取样频 率, (1)f(3) (2)f0 (3)f0*f2) (4)f)+f(0 (1)(1)解:由傅里叶变换的尺度变换特性可知 FLf(31=F(2z) 两台-人,B人= 由时域取样定理可知,最小取样频率/满足 f≥2fn=600E (2))(2)解:由傅里叶变换卷积定理可知 FV'-2aFfo*FUo例 FUFU1 由卷积性质可知最高/:=2/。=200:,则由时域取样定理可知,最小取样频 率了应满足 f,≥2f=400HE (3)(3)由傅里叶变换的线性性质可知 FUFQ201-F2x) 又由傅里叶变换时域卷积定理可知 FL/0*f2=FU20…)FU2r 则最高频率为人=人=100:由时域取样定理可知最高取样频率/应满起 f,≥2f=200E (4)(4)由傅里叶变换的线性可知 FLf()+(20]=FLf(]+FL()] FU)F2FU2) 则由(2)中结果可知信号f0)+f(2)的最高频率为人=2以。=200:,由时域取样 定理可知最高取样频率应满足
4.48 有限频带信号 f (t) 的最高频率为 100Hz,若对下列信号进行时域取样,求最小取样频 率 s f 。 (1) f (3t) (2) ( ) 2 f t (3) f (t) * f (2t) (4) ( ) ( ) 2 f t f t (1) (1) 解:由傅里叶变换的尺度变换特性可知 ) 3 ( 2 3 1 [ (3 )] f F f t F j 则有 m m f f 3 1 ,即 f f Hz m m 3 300 1 由时域取样定理可知,最小取样频率 s f 满足 f f Hz s m 2 600 (2) (2) 解:由傅里叶变换卷积定理可知 [ 2 ]* [ 2 ] 2 1 [ ( )]* [ ( )] 2 1 [ ( )] 2 F j f F j f F f t F f t F f t 由卷积性质可知最高 f f Hz m m 2 200 2 ,则由时域取样定理可知,最小取样频 率 s f 应满足 f f Hz s m 2 400 2 (3) (3) 由傅里叶变换的线性性质可知 ) 2 ( 2 2 1 [ (2 )] f F f t F j 又由傅里叶变换时域卷积定理可知 ) 2 ( 2 2 1 [ ( ) * (2 )] ( 2 ) f F f t f t F j f F j 则最高频率为 f f Hz m m 100 3 由时域取样定理可知最高取样频率 s f 应满足 f f Hz s m 2 200 3 (4) (4) 由傅里叶变换的线性可知 ( 2 ) * ( 2 ) 2 1 ( 2 ) [ ( ) (2 )] [ ( )] [ ( )] 2 2 F j f F j f F j f F f t f t F f t F f t 则由(2)中结果可知信号 ( ) (2 ) 2 f t f t 的最高频率为 f f Hz m m 2 200 4 ,由时域取样 定理可知最高取样频率 s f 应满足