
第8章高级神经网络

8.1模糊RBF网络 在模糊系统中,模糊集、隶属度函数和模糊规则 的设计是建立在经验知识基础上的。这种设计方法存 在很大的主观性。将学习机制引到模糊系统中,使模 糊系统能够通过不断学习来修改和完善隶属函数和模 糊规则,是模糊系统的发展方向

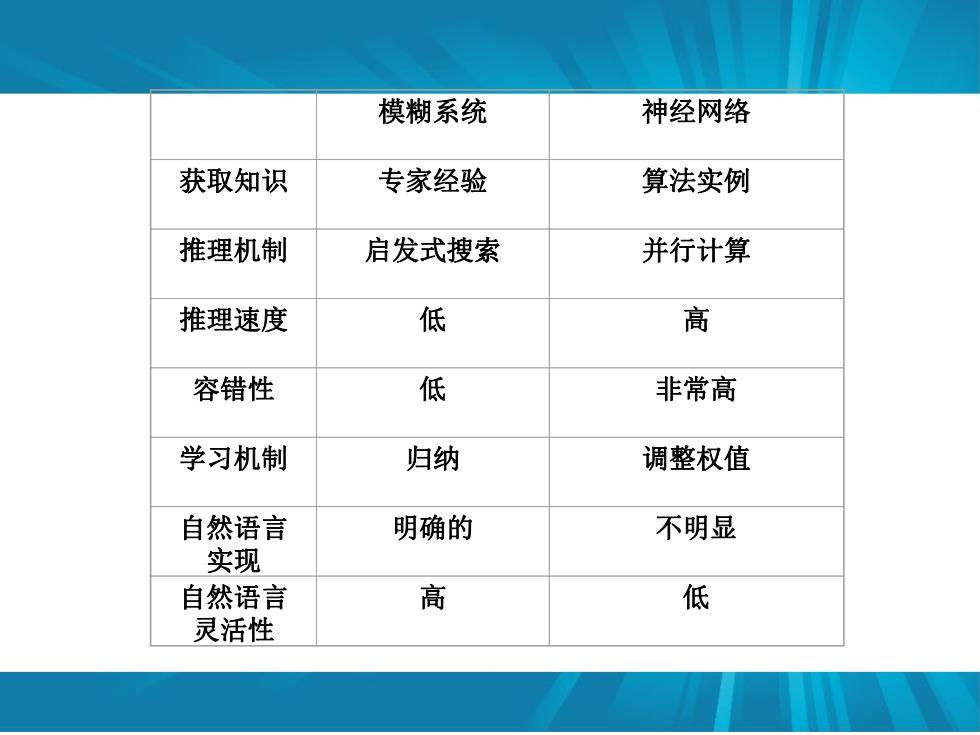
模糊系统与模糊神经网络既有联系又有区别, 其联系表现为模糊神经网络在本质上是模糊系统的 实现,其区别表现为模糊神经网络又具有神经网络 的特性。 神经网络与模糊系统的比较见表8-1。模糊神 经网络充分地利用了神经网络和模糊系统各自的优 点,因而受到了重视
• 模糊系统与模糊神经网络既有联系又有区别, 其联系表现为模糊神经网络在本质上是模糊系统的 实现,其区别表现为模糊神经网络又具有神经网络 的特性。 • 神经网络与模糊系统的比较见表8-1。模糊神 经网络充分地利用了神经网络和模糊系统各自的优 点,因而受到了重视
模糊系统 神经网络 获取知识 专家经验 算法实例 推理机制 启发式搜索 并行计算 推理速度 低 高 容错性 低 非常高 学习机制 归纳 调整权值 自然语言 明确的 不明显 实现 自然语言 高 低 灵活性
模糊系统 神经网络 获取知识 专家经验 算法实例 推理机制 启发式搜索 并行计算 推理速度 低 高 容错性 低 非常高 学习机制 归纳 调整权值 自然语言 实现 明确的 不明显 自然语言 灵活性 高 低

● 将神经网络的学习能力引到模糊系统中,将模 糊系统的模糊化处理、模糊推理、精确化计算通过 分布式的神经网络来表示是实现模糊系统自组织、 自学习的重要途径。在模糊神经网络中,神经网络 的输入、输出节点用来表示模糊系统的输入、输出 信号,神经网络的隐含节点用来表示隶属函数和模 糊规则,利用神经网络的并行处理能力使得模糊系 统的推理能力大大提高
• 将神经网络的学习能力引到模糊系统中,将模 糊系统的模糊化处理、模糊推理、精确化计算通过 分布式的神经网络来表示是实现模糊系统自组织、 自学习的重要途径。在模糊神经网络中,神经网络 的输入、输出节点用来表示模糊系统的输入、输出 信号,神经网络的隐含节点用来表示隶属函数和模 糊规则,利用神经网络的并行处理能力使得模糊系 统的推理能力大大提高

模糊神经网络在本质上是将常规的神经网络赋 予模糊输入信号和模糊权值,其学习算法通常是神 经网络学习算法或其推广。模糊神经网络技术己经 获得了广泛的应用,当前的应用主要集中在以下几 个领域:模糊回归、模糊控制、模糊专家系统、模 糊矩阵方程、模糊建模和模糊模式识别。 模糊神经网络是将模糊系统和神经网络相结合 而构成的网络。利用RBF网络与模糊系统相结合, 构成了模糊RBF网络
• 模糊神经网络在本质上是将常规的神经网络赋 予模糊输入信号和模糊权值,其学习算法通常是神 经网络学习算法或其推广。模糊神经网络技术已经 获得了广泛的应用,当前的应用主要集中在以下几 个领域:模糊回归、模糊控制、模糊专家系统、模 糊矩阵方程、模糊建模和模糊模式识别。 • 模糊神经网络是将模糊系统和神经网络相结合 而构成的网络。利用RBF网络与模糊系统相结合, 构成了模糊RBF网络

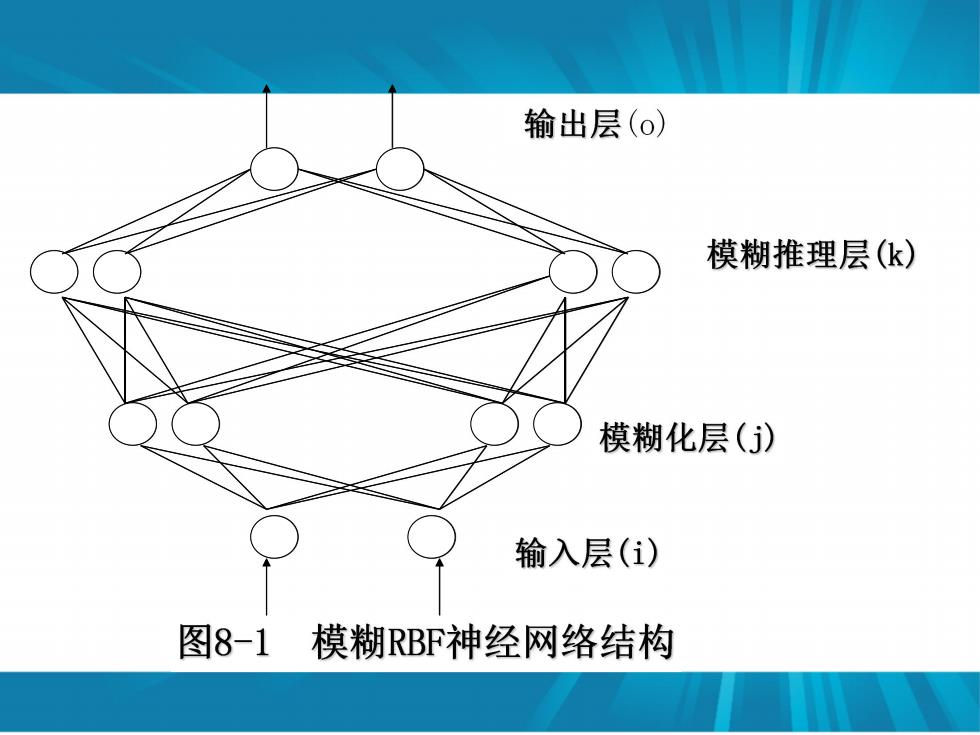
8.1.1网络结构 采用图8-1所示的模糊神经网络系统,其模糊推理 系统主要由输入层、模糊化层、模糊相联层、模糊后 相连层和输出层构成
输出层(o) 模糊推理层(k) 模糊化层(j) 输入层(i) 图8-1模糊RBF神经网络结构

模糊RBF网络中信号传播及各层的功能表示如下 第一层:输入层 该层的各个节点直接与输入量的各个分量连 接,将输入量传到下一层。对该层的每个节点的输 入输出表示为: f1()=x
i f (i) x 1

第二层:隶属函数层,即模糊化层 该层的每个节点具有隶属函数的功能,采用高斯函 数作为隶属函数。对第j个节点: f2(i,j)=exp(net) neu3-(io-cg)2 (6)2 其中C可和bj分别是第i个输入变量的第j个模糊 集合高斯函数的均值和标准差
第二层:隶属函数层,即模糊化层 该层的每个节点具有隶属函数的功能,采用高斯函 数作为隶属函数。对第j个节点: 其中 和 分别是第i个输入变量的第j个模糊 集合高斯函数的均值和标准差。 2 2 2 1 ( ) ( ( ) ) j ij j b f i c net ( , ) exp( ) 2 2 j f i j net ij c j b