
绝 CH2辨识理论基础及古典辨识法 1 202414120
2024/4/20 1 CH2 辨识理论基础及古典辨识法

CH2辨识理论基础及古典辨识法 本章要点: 1随机过程的基本概念及其数学描述; 2线性系统在随机输入下的响应; 3随机序列和白噪声及其产生方法及其MATLAB仿 真; 4基于相关函数的古典辨识方法; 难点: 相关函数及其古典辨识方法 白噪声及其产生方法 2 2024/4/20
2024/4/20 2 CH2 辨识理论基础及古典辨识法 本章要点: 1 随机过程的基本概念及其数学描述; 2 线性系统在随机输入下的响应; 3 随机序列和白噪声及其产生方法及其MATLAB仿 真; 4 基于相关函数的古典辨识方法; 难点: 相关函数及其古典辨识方法 白噪声及其产生方法

■2.1随机过程基本概念及其数学描述 2.2谱密度与相关函数 2.3线性系统在随机输入下的响应 ■2.4白噪声产生方法及其仿真 ■2.5古典辨识方法 ■2.6小结及习题 202414120
◼ 2.1 随机过程基本概念及其数学描述 ◼ 2.2 谱密度与相关函数 ◼ 2.3 线性系统在随机输入下的响应 ◼ 2.4 白噪声产生方法及其仿真 ◼ 2.5 古典辨识方法 ◼ 2.6 小结及习题 2024/4/20

2.1随机过程基本概念及其数学描述 ■2.1.1基本概念 在科学技术领域中,人们观察到各式各样的 事物变化过程。有些变化过程具有明确的规律性, 例如自由落体运动,电容充电过程等,这些称为 确定性过程。还有些变化过程具有偶然性,例如 电子放大器的零点漂移、风浪中海面的起伏等, 人们无法预知下一时刻将会发生什么情况,这些 称为随机过程。所谓“随机过程”就是指大量样 所构成的总体。 202414120
2024/4/20 4 2.1 随机过程基本概念及其数学描述 ◼ 2.1.1 基本概念 在科学技术领域中,人们观察到各式各样的 事物变化过程。有些变化过程具有明确的规律性, 例如自由落体运动,电容充电过程等,这些称为 确定性过程。还有些变化过程具有偶然性,例如 电子放大器的零点漂移、风浪中海面的起伏等, 人们无法预知下一时刻将会发生什么情况,这些 称为随机过程。所谓“随机过程”就是指大量样 4本所构成的总体

1)随机过程数学描述 为了对随机过程x()进行数学描述,应注意以下几点: ①在每一孤立的瞬间x()的取值是随机的,它是一个随机变量。这就 引出随机过程一维空间概率密度卫,(x,t)的概念。 ②延时间坐标轴看,x(t)是X的取值随时间变化的过程。为了完整描述 一个随机过程,还需反映不同的时刻X取值之间的联系。二维概率密 度P2(x,x24,2)代表X在t时刻X1t,时刻取值为,的概率密度。 这就是说p2(x,x2;t1,t2)dcdc2代表x(t) 相继通过随机过程图2.1中 dk和dx2两个小窗口的概率。 5 202414/20
2024/4/20 5 1)随机过程数学描述 为了对随机过程 进行数学描述,应注意以下几点: ① 在每一孤立的瞬间 的取值是随机的,它是一个随机变量。这就 引出随机过程一维空间概率密度 的概念。 ②延时间坐标轴看, 是 的取值随时间变化的过程。为了完整描述 一个随机过程,还需反映不同的时刻 取值之间的联系。二维概率密 度 代表 在 时刻 , 时刻 取值为 的概率密度。 这就是说 代表 相继通过随机过程图2.1中 和 两个小窗口的概率。 x(t) x(t) ( , ) 1 p x t x(t) x x ( , ; , ) 2 1 2 1 2 p x x t t x 1 t 1 x 2 1 2 1 2 1 2 p (x , x ;t ,t )dx dx x(t) dx 2 dx 2 t 2 x
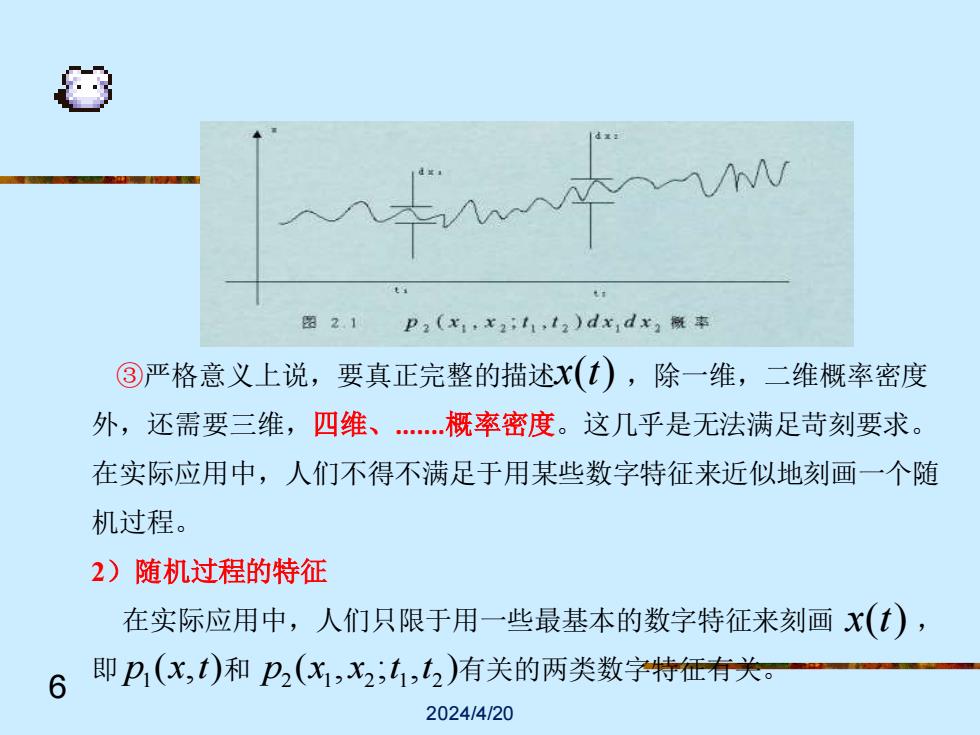
P2(x1,x211,t2)dx1dx2概率 ③严格意义上说,要真正完整的描述x(t),除一维,二维概率密度 外,还需要三维,四维、概率密度。这几乎是无法满足苛刻要求。 在实际应用中,人们不得不满足于用某些数字特征来近似地刻画一个随 机过程。 2)随机过程的特征 在实际应用中,人们只限于用一些最基本的数字特征来刻画x(), 6 即P(x,t)和P2(X1,x2t1,t2)有关的两类数字特征有关。 2024/14/20
2024/4/20 6 ③严格意义上说,要真正完整的描述 ,除一维,二维概率密度 外,还需要三维,四维、.......概率密度。这几乎是无法满足苛刻要求。 在实际应用中,人们不得不满足于用某些数字特征来近似地刻画一个随 机过程。 2)随机过程的特征 在实际应用中,人们只限于用一些最基本的数字特征来刻画 , 即 和 有关的两类数字特征有关。 x(t) x(t) ( , ) 1 p x t ( , ; , ) 2 1 2 1 2 p x x t t

如果平稳随机过程x()的各集合平均值等于相对应的时间平均值, 即: x=ux x(t)x(t+)=R,(t) (2.) 式中,x为随机过程x(t)的时间均值(指对dt的积分均值),ux为与 一维概率密度p,(x,t)有关的数字特征量集合均值(指对的积分的均 值),R,(口)为自相关函数。则称x(t)是各态遍历的平稳随机过程。 对于各态遍历的平稳随机过程,它的两个基本数字特征就可以只根据 一个很长的样本按下式计算: (2.2 7 R,()=lim 2024/4/20
2024/4/20 7 如果平稳随机过程 的各集合平均值等于相对应的时间平均值, 即: 式中, 为随机过程 的时间均值(指对 的积分均值), 为 与 一维概率密度 有关的数字特征量集合均值(指对 的积分的均 值), 为 自相关函数。则称 是各态遍历的平稳随机过程。 对于各态遍历的平稳随机过程,它的两个基本数字特征就可以只根据 一个很长的样本按下式计算: x(t) + = = ( ) ( ) ( ) x x x t x t R x u (2.1) x x(t) dt x u ( , ) 1 p x t dx ( ) Rx x(t) = + = → − → − x t x t dt T R x t dt T u T x T T T x ( ) ( ) 2 1 ( ) lim ( ) 2 1 lim (2.2)

实际上,只能使T取尽可能大的有限制 值,见图2.2假定T=NT,t=1T为采 样时间,则式(2.2)变为: N (2.3) 图22兴,和R(们的近似计复 1 N-/ R(R()= 以上讨论了一个随机过程单独存在时的情况。有时在同一个问题中涉 及两个互相有关的随机过程x()与y(t),例如一个人出现在过程的输入 侧,另一个出现在输出侧,则可用互相关函数和互协方差函数来描述它 8们之间的关系。 2024/14/20
2024/4/20 8 实际上,只能使T取尽可能大的有限制 值 值,见图2.2假定 , 为采 样 样时间 ,则式 变为: 以上讨论了一个随机过程单独存在时的情况。有时在同一个问题中涉 及两个互相有关的随机过程 与 ,例如一个人出现在过程的输入 侧,另一个出现在输出侧,则可用互相关函数和互协方差函数来描述它 们之间的关系。 T = NT0 0 = lT (2.2) + − − = = = N l k x x N k x x k x k l N R R l x k N u 1 1 ( ) ( ) 1 1 ( ) ( ) ( ) 1 (2.3) x(t) y(t)

互相关函数 R(t)△E{x(t)y(t+t)} 互协方差函数 Cs()ACov().y(t+AEx(t)-u,lIy(t+)-u] =R()-u,uy 若Cw(t)=0,廿-o<t<o,则称x()与y(t)互不相关。 2.1.2相关函数和协方差函数的性质 1)自相关函数和自协方差函数具有以下性质: (1)R(0)=E{(t)z(t+0)}=p2≥0 (2.6) (2)根据R(x)的定义,显然有R(-t)=R(),这说明R,(t)对称于 纵轴。 (3)R(r)≤R(0) 2.7 9 2024/4/20
2024/4/20 9 互相关函数 互协方差函数 若 , ,则称 与 互不相关。 2.1.2 相关函数和协方差函数的性质 1)自相关函数和自协方差函数具有以下性质: (1) (2)根据 的定义,显然有 ,这说明 对称于 纵轴。 (3) ( ) ( ) ( + ) = R E x t y t xy xy x y xy x y R u u C Cov x t y t E x t u y t u = − + − + − = = ( ) ( ) ( ), ( ) [ ( ) ][ ( ) ] Cxy ( ) = 0 − x(t) y(t) (0) ( ) ( 0) 0 2 Rx = E x t z t + =x (2.6) ( ) Rx ( ) ( ) Rx − = Rx ( ) Rx ( ) (0) Rx Rx (2.7)

(4)有时候设计的伪随机信号。例如M序列,具有周期性,称为“周期 性”随机过程。它们的自相关函数也具有周期性,即若x(t+T)=x(),则 R(t+T)=R(t)。 (5)根据x()均值不为零,则可分解成x()=y)+4,其中)是 均值为零的随机过程。此时: R,(t)=E()+4][y(t+x)+4]}=R,(x)+4 (2.8) 换言之x(t)中的直流成分使其自相关函数向上平移 (6)若出现x(t)均值为零,且不含有周期性成分,则当T很大时,x(t+x) 与x(t)必然是相互独立的,因而此时R(x)=0。 10 2.7分 2024/4/20
2024/4/20 10 (4)有时候设计的伪随机信号。例如M序列,具有周期性,称为“周期 性”随机过程。它们的自相关函数也具有周期性,即若 ,则 。 (5)根据 均值不为零,则可分解成 ,其中 是 均值为零的随机过程。此时: 换言之 中的直流成分使其自相关函数向上平移 。 (6)若出现 均值为零,且不含有周期性成分,则当 很大时, 与 必然是相互独立的,因而此时 。 x(t) y(t) (2.8) (2.7) x(t +T) = x(t) ( ) ( ) Rx +T = Rx x(t) ux x(t) = y(t) + 2 ( ) [ ( ) ][ ( ) ] ( ) x x ux Ry ux R = E y t +u y t + + = + 2 x u x(t) x(t + ) x(t) Rx ( ) = 0