
第一章原子结构和元素周期律 §1离子键理论 1916年德国科学家Kossel(科塞尔)提出离子键理论。 一离子键的形成 1形成过程 以NaCI为例。 第一步电子转移形成离子: Na -e —Na+, CI+e一 CI- 相应的电子构型变化: 2s22p63s1—2s22p6, 3s23p5—3s23p6 形成Ne和Ar的稀有气体原子的结构,形成稳定离子。 第二步靠静电吸引,形成化学键
第一章 原子结构和元素周期律 §1 离子键理论 1916 年德国科学家Kossel ( 科塞尔 ) 提出离子键理论。 一 离子键的形成 1 形成过程 以 NaCl 为例 。 第一步 电子转移形成离子: Na - e —— Na+ , Cl + e —— Cl - 第二步 靠静电吸引,形成化学键。 相应的电子构型变化: 2s 2 2p 6 3s 1 —— 2s 2 2p 6 , 3s 2 3p 5 —— 3s 2 3p 6 形成 Ne 和 Ar 的稀有气体原子的结构,形成稳定离子
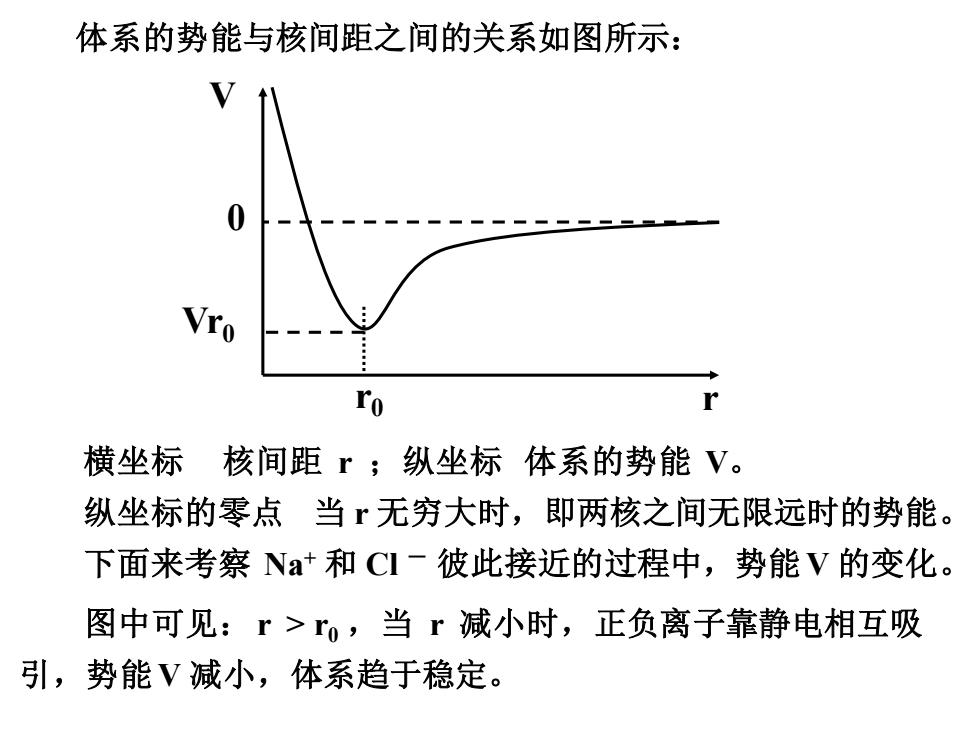
体系的势能与核间距之间的关系如图所示: 0 Vro ro r 横坐标 核间距r;纵坐标体系的势能V。 纵坐标的零点当无穷大时,即两核之间无限远时的势能。 下面来考察Na+和CI一彼此接近的过程中,势能V的变化。 图中可见:r>r0,当r减小时,正负离子靠静电相互吸 引,势能V减小,体系趋于稳定
横坐标 核间距 r ;纵坐标 体系的势能 V。 纵坐标的零点 当 r 无穷大时,即两核之间无限远时的势能。 下面来考察 Na+ 和 Cl - 彼此接近的过程中,势能V 的变化。 体系的势能与核间距之间的关系如图所示: V 0 Vr0 r0 r 图中可见:r > r0 ,当 r 减小时,正负离子靠静电相互吸 引,势能V 减小,体系趋于稳定
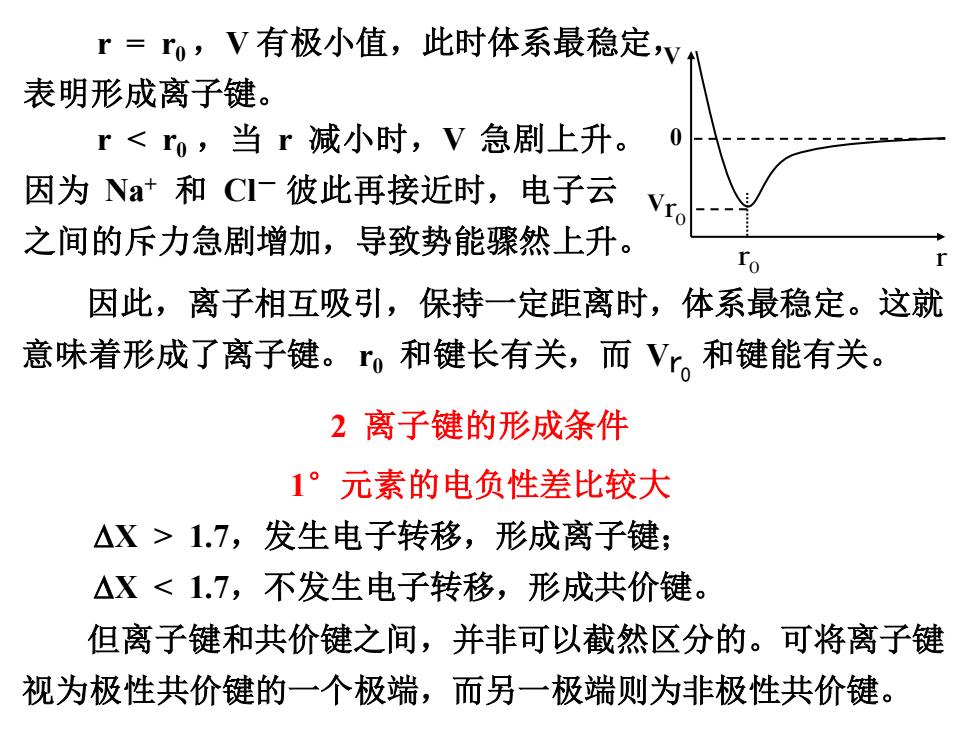
r=ro,V有极小值,此时体系最稳定v 表明形成离子键。 r1.7,发生电子转移,形成离子键; △X<1.7,不发生电子转移,形成共价键。 但离子键和共价键之间,并非可以截然区分的。可将离子键 视为极性共价键的一个极端,而另一极端则为非极性共价键
r = r0 ,V 有极小值,此时体系最稳定, 表明形成离子键。 2 离子键的形成条件 1°元素的电负性差比较大 X > 1.7,发生电子转移,形成离子键; X < 1.7,不发生电子转移,形成共价键。 但离子键和共价键之间,并非可以截然区分的。可将离子键 视为极性共价键的一个极端,而另一极端则为非极性共价键。 因此,离子相互吸引,保持一定距离时,体系最稳定。这就 意味着形成了离子键。 r0 和键长有关,而 V r0 和键能有关。 V 0 V 0 r 0 r r r < r0 ,当 r 减小时,V 急剧上升。 因为 Na+ 和 Cl- 彼此再接近时,电子云 之间的斥力急剧增加,导致势能骤然上升

极性增大 非极性共价键 极性共价键 离子键 化合物中不存在百分之百的离子键,即使是NaF的化学键, 其中也有共价键的成分。即除离子间靠静电相互吸引外,尚有共 用电子对的作用。 △X>1.7,实际上是指离子键的成分大于50%。 2°易形成稳定离子 Na+2s22p6,C-3s23p6,达到稀有气体式稳定结构。 Ag+4d10,Zn2+3d10,d轨道全充满的稳定结构。 只转移少数的电子,就达到稳定结构。 而C和Si原子的电子结构为s2p2,要失去或得到4e,才 能形成稳定离子,比较困难。所以一般不形成离子键。如
极性增大 非极性共价键 极性共价键 离子键 化合物中不存在百分之百的离子键,即使是 NaF 的化学键, 其中也有共价键的成分。即除离子间靠静电相互吸引外,尚有共 用电子对的作用。 X > 1.7 ,实际上是指离子键的成分大于 50 %。 2° 易形成稳定离子 Na + 2s 2 2p 6 ,Cl- 3s 2 3p 6 ,达到稀有气体式稳定结构。 Ag + 4d10 , Zn 2 + 3d10 , d 轨道全充满的稳定结构。 只转移少数的电子,就达到稳定结构。 而 C 和 Si 原子的电子结构为s 2 p 2 ,要失去或得到 4 e,才 能形成稳定离子,比较困难。所以一般不形成离子键。如

CCI4、SiF4等,均为共价化合物。 3°形成离子键时释放能量多 Na (s)1/2 CI2(g)=NaCl s)AH=-410.9 kJ-mol- 1 在形成离子键时,以放热的形式,释放较多的能量。 二离子键的特征 1作用力的实质是静电引力 F91·92 q1,q2分别为正负离子所带电量, r2 r为正负离子的核间距离。 2离子键无方向性和饱和性 与任何方向的电性不同的离子相吸引,所以无方向性; 且只要是正负离子之间,则彼此吸引,即无饱和性。 学习了共价键以后,会加深对这个问题的理解
3°形成离子键时释放能量多 Na ( s ) + 1/2 Cl 2 ( g ) = NaCl ( s ) H = -410.9 kJ·mol- 1 在形成离子键时,以放热的形式,释放较多的能量。 CCl 4 、SiF4 等,均为共价化合物。 二 离子键的特征 1 作用力的实质是静电引力 2 1 2 r q q F q1 ,q2 分别为正负离子所带电量, r 为正负离子的核间距离。 2 离子键无方向性和饱和性 与任何方向的电性不同的离子相吸引,所以无方向性; 且只要是正负离子之间,则彼此吸引,即无饱和性。 学习了共价键以后,会加深对这个问题的理解

三离子键的强度 1键能和晶格能 键能(以NaCI为例)1mol气态NaCI分子,离解成气 体原子时,所吸收的能量,用E:表示。 NaCI(g)=Na(g)+CI(g) △H=E: 键能E越大,表示离子键越强。 晶格能气态的正负离子,结合成1 mol NaC1晶体时,放 出的能量,用U表示。 Na(g)+CI(g)=NaCI(s) △H=一U 晶格能U越大,则形成离子键得到离子晶体时放出的能量 越多,离子键越强。 键能和晶格能,均能表示离子键的强度,而且大小关系一致。 晶格能比较常用
三 离子键的强度 1 键能和晶格能 键能 ( 以 NaCl 为例 ) 1 mol 气态 NaCl 分子,离解成气 体原子时,所吸收的能量,用 Ei 表示。 NaCl ( g ) = Na ( g ) + Cl ( g ) H = Ei 键能 Ei 越大,表示离子键越强。 晶格能 气态的正负离子,结合成 1 mol NaCl 晶体时,放 出的能量,用 U 表示。 Na + ( g ) + Cl- ( g ) = NaCl ( s ) H = -U 晶格能 U 越大,则形成离子键得到离子晶体时放出的能量 越多,离子键越强。 键能和晶格能,均能表示离子键的强度,而且大小关系一致。 晶格能比较常用
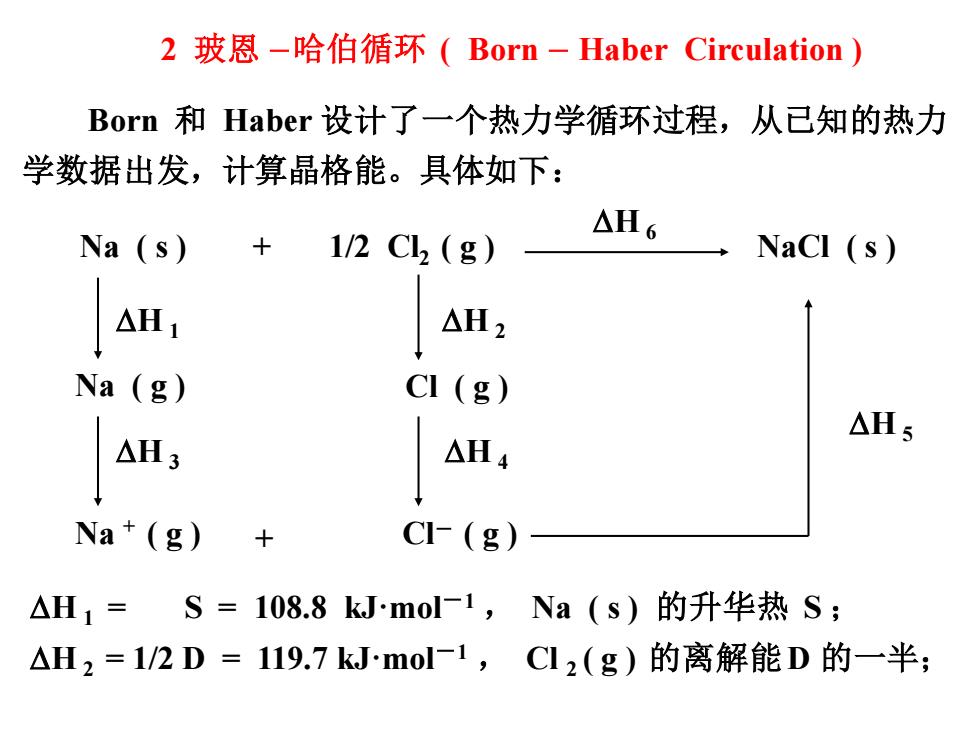
2玻恩-哈伯循环(Born-Haber Circulation) Borm和Haber设计了一个热力学循环过程,从已知的热力 学数据出发,计算晶格能。具体如下: △H6 Na (s) 1/2CL2(g) △H1 △H2 Na (g) CI (g) △H5 △H4 Na (g) CI-(g) △H1=S=108.8 kJmol-1,Na(s)的升华热S; △H2=1/2D=119.7 kJ.mol-1,Cl2(g)的离解能D的一半;
2 玻恩 -哈伯循环 ( Born - Haber Circulation ) Born 和 Haber 设计了一个热力学循环过程,从已知的热力 学数据出发,计算晶格能。具体如下: Na ( g ) H 1 Na + ( g ) H 3 Na ( s ) + 1/2 Cl2 ( g ) NaCl ( s ) H 6 H 1 = S = 108.8 kJ·mol-1 , Na ( s ) 的升华热 S ; H 2 = 1/2 D = 119.7 kJ·mol-1 , Cl 2 ( g ) 的离解能D 的一半; H 2 Cl ( g ) H 4 Cl- ( g ) H 5 +
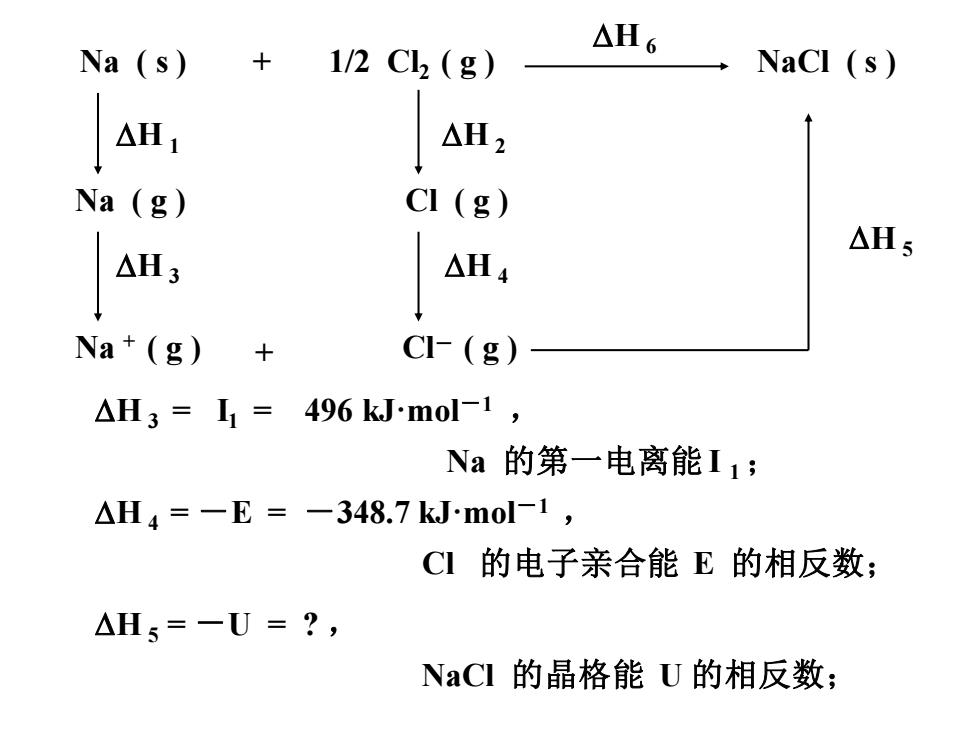
△H6 Na (s) 1/2C2(g) NaCI (s) △H1 △H2 Na (g) CI (g) △Hs △H3 △H4 Na (g) CI(g) △H3=I1=496 kJ.mol-1, Na的第一电离能I1; △H4=-E=-348.7 kJ.mol-1, CI的电子亲合能E的相反数; △Hs=一U=?, NaCI的晶格能U的相反数;
Na ( g ) H 1 Na + ( g ) H 3 Na ( s ) + 1/2 Cl2 ( g ) NaCl ( s ) H 6 H 2 Cl ( g ) H 4 Cl- ( g ) H 5 + H 3 = I1 = 496 kJ·mol-1 , Na 的第一电离能I 1 ; H 4 = -E = -348.7 kJ·mol-1 , Cl 的电子亲合能 E 的相反数; H 5 = -U = ? , NaCl 的晶格能 U 的相反数;
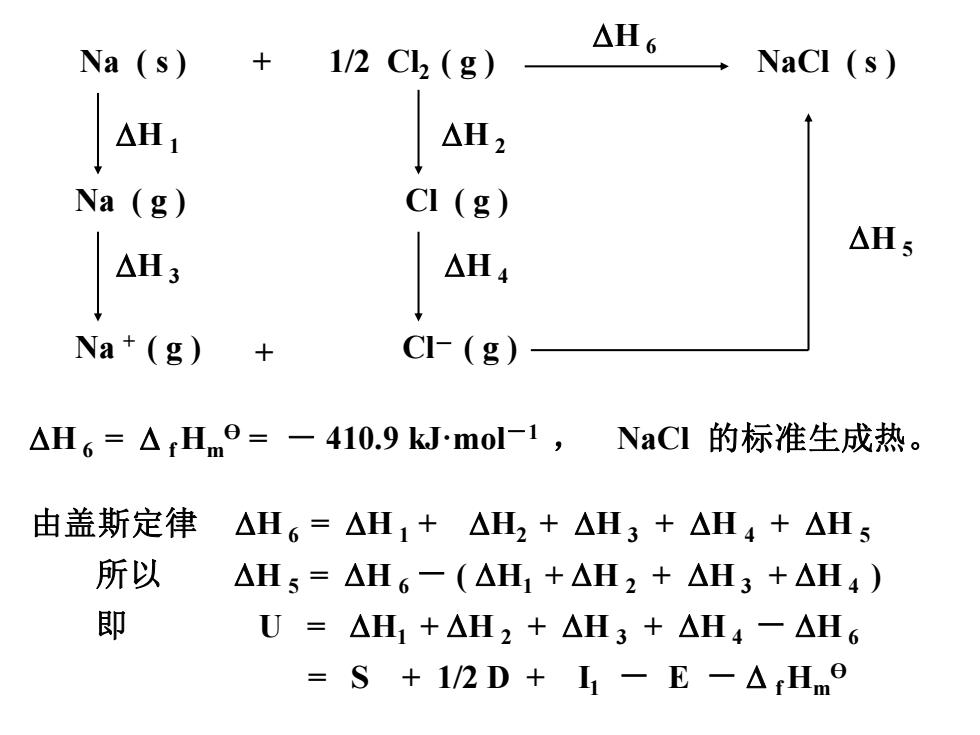
△H6 Na (s)+ 1/2C2(g) NaCl (s) △H1 △H2 Na(g) CI (g) △Hs AH, △H4 Na+(g) CI-(g) △H6=△rHm=一410.9kmol-1,NaCI的标准生成热。 由盖斯定律△H6=△H1+△H2+△H3+△H4+△Hs 所以 △Hs=△H6一(△H1+△H2+△H3+△H4) 即 U=△H1+△H2+△H3+△H4-△H6 =S+1/2D+1-E-△Hm9
Na ( g ) H 1 Na + ( g ) H 3 Na ( s ) + 1/2 Cl2 ( g ) NaCl ( s ) H 6 H 2 Cl ( g ) H 4 Cl- ( g ) H 5 + H 6 = f Hm Ө = - 410.9 kJ·mol-1 , NaCl 的标准生成热。 由盖斯定律 H 6 = H 1 + H2 + H 3 + H 4 + H 5 所以 H 5 = H 6 - ( H1 + H 2 + H 3 + H 4 ) 即 U = H1 + H 2 + H 3 + H 4 - H 6 = S + 1/2 D + I1 - E - f Hm Ө

U=108.8+119.7+496-348.7+410.9 =786.7(kJ-mol-1) 以上关系称为Borm一Haber循环。 利用盖斯定律,也可以计算NaCI的离子键的键能。 △H=Ei NaCl (g) Na (g) + C1(g) Na(g)+CI (g)- AHs=-Ei NaCI (g) AH, AH: △H3 Nat(g)+CI-(g) NaCl (s)
U = 108.8 + 119.7 + 496 - 348.7 + 410.9 = 786.7 ( kJ·mol-1 ) 以上关系称为 Born - Haber 循环 。 利用盖斯定律,也可以计算 NaCl 的离子键的键能。 NaCl ( g ) Na ( g ) + Cl ( g ) H = E i Na+ ( g ) H1 H4 H2 Cl-( g ) H3 + NaCl ( s ) Na ( g ) + Cl ( g ) NaCl ( g ) H5 = - E i