
第九章多元线性回归与多项式回归 直线回归研究的是一个依变量与一个自变量之 间的回归问题,但是,在畜禽、水产科学领域 的许多实际问题中,影响依变量的自变量往往 不止一个,而是多个,比如绵羊的产毛量这 变量同时受到绵羊体重、胸围、体长等多个变 量的影响,因此需要进行一个依变量与多个自 变量间的回归分析,即多元回归分析 (multiple regression analysis) 其中最为简单、常用并且具有基础性质的是多 元线性回归分析(multiple linear regression analysis)
第九章 多元线性回归与多项式回归 ◼ 直线回归研究的是一个依变量与一个自变量之 间的回归问题,但是,在畜禽、水产科学领域 的许多实际问题中,影响依变量的自变量往往 不止一个,而是多个,比如绵羊的产毛量这一 变量同时受到绵羊体重、胸围、体长等多个变 量的影响,因此需要进行一个依变量与多个自 变量间的回归分析,即多元回归分析 (multiple regression analysis),而 其中最为简单、常用并且具有基础性质的是多 元线性回归分析(multiple linear regression analysis)

第一节 多元线性回归分析 多元线性回归分析的基本任务包括:根据依 变量与多个自变量的实际观测值建立依变量 对多个自变量的多元线性回归方程;检验 分析各个自变量对依自变量的综合线性影响 的显著性;检验、分析各个自变量对依变量 的单纯线性影响的显著性,选择仅对依变量 有显著线性影响的自变量,建立最优多元线 性回归方程;评定各个自变量对依变量影响 的相对重要性以及测定最优多元线性回归方 程的偏离度等
第一节 多元线性回归分析 ◼ 多元线性回归分析的基本任务包括:根据依 变量与多个自变量的实际观测值建立依变量 对多个自变量的多元线性回归方程;检验、 分析各个自变量对依自变量的综合线性影响 的显著性;检验、分析各个自变量对依变量 的单纯线性影响的显著性,选择仅对依变量 有显著线性影响的自变量,建立最优多元线 性回归方程;评定各个自变量对依变量影响 的相对重要性以及测定最优多元线性回归方 程的偏离度等
一、多元线性回归方程的建立 (一)多元线性回归的数学模型 设依变量y与自变量x1、X2、、×m共有 n组实际观测数据: 变量 序号 X1 X2 Xm 1 y1 X11 X21 Xm1 2 V2 ×12 X22 Xm2 Xin X2n Xmn
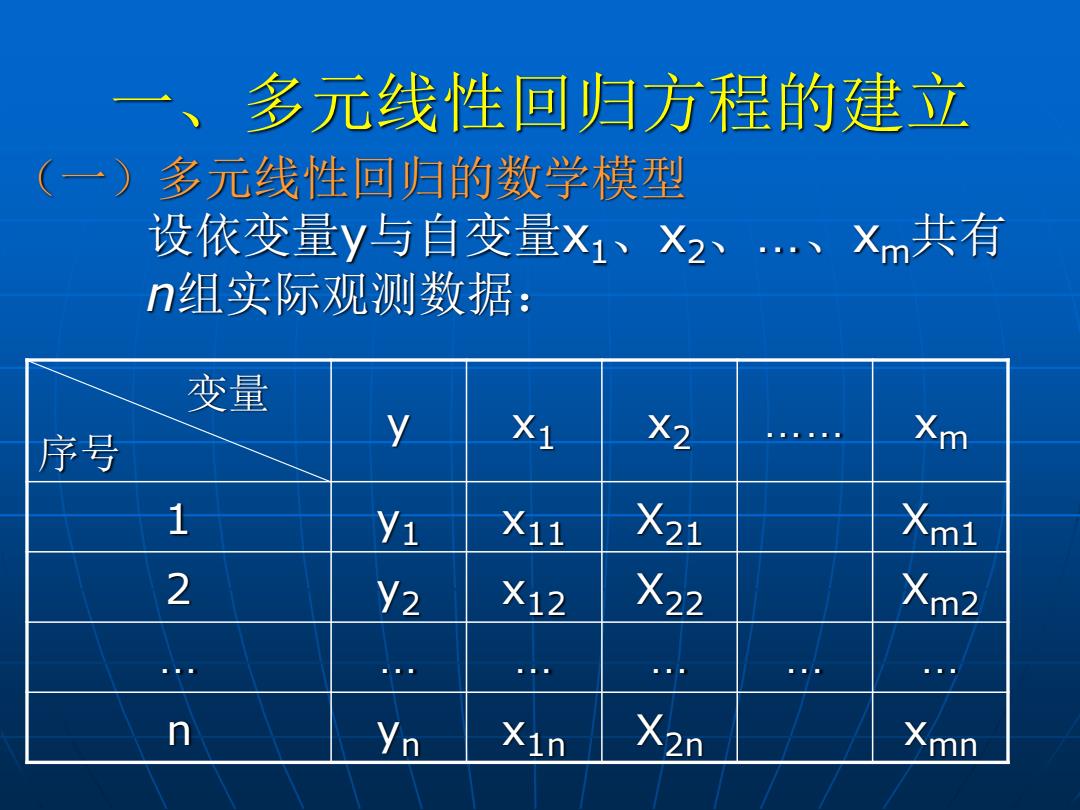
一、多元线性回归方程的建立 (一)多元线性回归的数学模型 设依变量y与自变量x1、x2、…、xm共有 n组实际观测数据: 变量 序号 y x1 x2 …… xm 1 y1 x11 X21 Xm1 2 y2 x12 X22 Xm2 … … … … … … n yn x1n X2n xmn

假定依交量y与自变量X1、X2、、Xm间存在 线性关系,其数学模型为: yi=Bo+B+Bx2+Bmxmi +j j=1,2,…n) 式中,X1、X2、、Xm为可以观测的一般变 量(或为可以观测的随机变量);y为可以观 测的随机变量,随X1、X2、、Xm而变,受 试验误差影响: £,为相互独立且都服从 N(0,σ2)的随机变量。我们可以根据实际观测 值对Bo、B、B2、Bm以及方差σ2作出 估计
◼ 假定依变量y与自变量x1、x2、…、xm间存在 线性关系,其数学模型为: (j=1,2,…,n) 式中,x1、x2、…、xm为可以观测的一般变 量(或为可以观测的随机变量);y为可以观 测的随机变量,随x1、x2、…、xm而变,受 试验误差影响; 为相互独立且都服从 的随机变量。我们可以根据实际观测 值对 以及方差 作出 估计。 j j j m mj j y = + x + x + ...+ x + 0 1 1 2 2 j (0, ) 2 N 、 、 、、 m ... 0 1 2 2

(二)建立多元线性回归方程 设y对X、x2、…、xm的m元线性回归方程为: =b+bx +b2x2++bnm 其中的b、b b bm 为 Po、B1P2、Pm的最小二乘估计值。 即b、b、b2、… bm应使实际观测值 y 与回归估计值的偏差平方和最小
(二)建立多元线性回归方程 设 y 对 1 x 、 2 x 、…、xm 的m元线性回归方程为: y=b0 +b1 x1+b2 x2 ++bmxm ˆ 其中的 b0 、 b1 、 b2 、…、 bm 为 0、 1、 2 ...、 m 的最小二乘估计值。 即 0 b 、b1、b2 、…、bm应使实际观测值 y 与回归估计值 yˆ 的偏差平方和最小

令 O=(y- =∑y,-b-bxy-bxy--bmxw】 1 Q为关于bn、、、…、bm的m+1元 函数。 根据微分学中多元函数求极值的方法, 若使Q达到最小,则应有:
令 = = − n j j j Q ( y ˆy ) 1 2 = = − − − − − n j j j j m mj y b b x b x b x 1 2 0 1 1 2 2 ( ) Q为关于 0 b 、 1b 、 2 b 、…、bm 的 m +1 元 函数。 根据微分学中多元函数求极值的方法, 若使Q 达到最小,则应有:

, =2>v,-h-bpy-bxy--Bry)=0 0=-20,-6=4与-6--w)-0 =1 (i=1、2、…、 m
= =− − − − − − = n j j j j m mj y b bx b x b x b Q 1 0 1 1 2 2 0 2 ( ) 0 = =− − − − − − = n j ij j j j m mj i x y b b x b x b x b Q 1 0 1 1 2 2 2 ( ) 0 (i =1、2、…、m )

经整理得: nbo+ (②x)b+(②x2b2++( ②xm)bm=马 ②xh+②xb+②2b2++②xm)bm=2xy 区x2b+②xxh+②b++②2Xm )bm= ②xmh,+②xmx)b+(②m)b2++②mbn=2xmJy
◼ 经整理得: + + + + = + + + + = + + + + = + + + + = x b x x b x x b x b x y x b x x b x b x x b x y x b x b x x b x x b x y nb x b x b x b y m m m m m m m m m m m m ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 0 1 1 2 2 2 2 2 2 2 0 2 1 1 2 1 1 2 2 1 1 2 1 0 1 0 1 1 2 2

由方程组中的第一个方程可得 b0=下-bx1-b2x2-…-bmXm 即 b0=-∑b,x i三1 其中:下=∑-之 n j=l n j=
由方程组中的第一个方程可得 m m b = y − b x − b x −− b x 0 1 1 2 2 即 = = − m i i i b y b x 1 0 1 , 1 : 1 1 = = = = n j i ij n j j x n y x n 其中 y

若记 8,-2-,8,=立y,- j=1 j=1 SPk=∑(y-,x-k)=SPa j=1 n SPo=∑(x)-,yy-) j=1 (i、k=、2、…、m;i≠k)
若记 ( ) , 1 2 = = − n j i ij i SS x x = = − n j y j SS y y 1 2 ( ) = = − − = n j ik ij i kj k SPki SP x x x x 1 ( )( ) = = − − n j io ij i j SP x x y y 1 ( )( ) (i 、k=1、 2 、…、 m ; i k)