
响应面(RESPONSE SURFACE)分析讲义 徐向宏编 (甘肃农业大学) 2009年2月
响应面(RESPONSE SURFACE)分析讲义 徐向宏 编 (甘肃农业大学) 2009 年 2 月
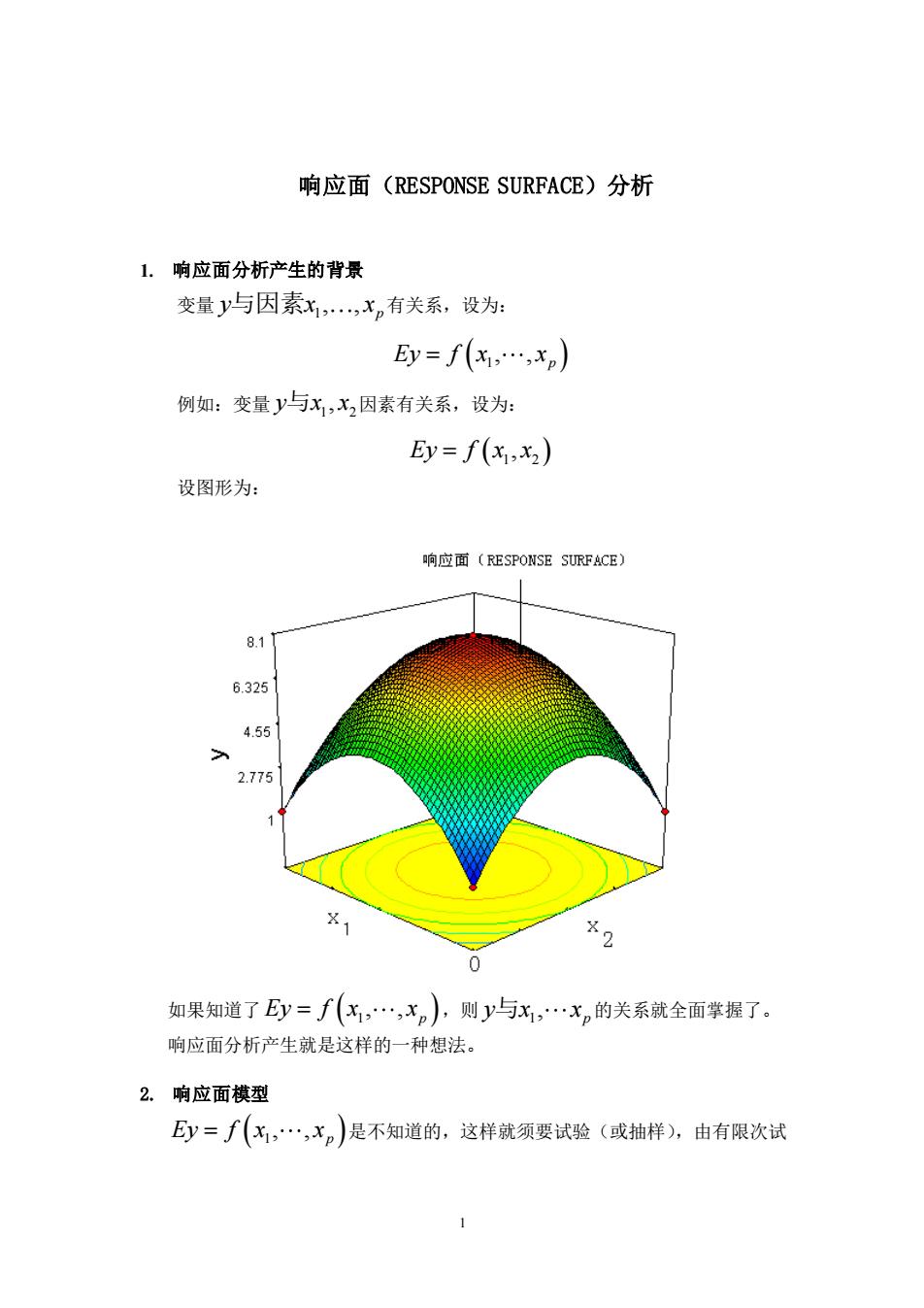
响应面(RESPONSE SURFACE)分析 1.响应面分析产生的背景 变量y与因素x,,x,有关系,设为: Ey=f(x,…,xp) 例如:变量y与x,x2因素有关系,设为: Ey=f(xx2) 设图形为: 响应面(RESPONSE SURFACE) 8.1 6.325 4.55 2.775 1 X 2 0 如果知道了y=f(x,,xp),则y与x,…x,的关系就全面掌握了。 响应面分析产生就是这样的一种想法。 2.响应面模型 y=∫(飞,…,xp)是不知道的,这样就须要试验(或抽样),由有限次试
1 响应面(RESPONSE SURFACE)分析 1. 响应面分析产生的背景 变量 1 , , p y x x 与因素 有关系,设为: Ey f x x = ( 1 , , p ) 例如:变量 1 2 y x x 与 , 因素有关系,设为: Ey f x x = ( 1 2 , ) 设图形为: 如果知道了 Ey f x x = ( 1 , , p ) ,则 1 , p y x x 与 的关系就全面掌握了。 响应面分析产生就是这样的一种想法。 2. 响应面模型 Ey f x x = ( 1 , , p ) 是不知道的,这样就须要试验(或抽样),由有限次试

验所得试验数据来估计y=f(x,…,x)(由部分来说明全体)。 哪么用什么样的模型来估计Ey=∫(x,…,x。)呢?在数学分析上已有麦 克劳林或泰勒展开式即:f(,)÷f(0)+(O) .f"(0) x2. 1 21 般都能满足(收敛),又生物科学领域变量间的特点,因此用 y=f(x,…,xp)≈a+bx+…+cxp+…+d2+…+ex,2+ X2…+g,-X,模型。 综上所述:试验得试验点: (x1,…xp1y),,(xa,xnmy) 估计出 y=f(x,…,xp)≈a+bx+…+cxp+…+d2+…+ex,2+ x2…+g,-1Xn的系数a,b,…,如果可用(检验),则X,…x,与y的关 系就全面掌握了。 3.响应面分析的试验设计(DOE一一Design of Exprement)一用Design-Expert7 软件 试验点(x1,…xp1乃?),…,(xn,…Xmn2 yn?)选择哪些点才能比较科 学地反映客观实际呢(包括试验次数要尽可能少、自变量间正交等)?这就是称 为试验设计研究。响应面分析的试验设计有: 中心组合设计(Central Composite Design-一CCD,二次正交旋转组合设计); BOX设计(Box-Behnken设计): D-optimal设计(2次饱和D一最优设计) 均匀设计: 田口设计: * 常用的是中心复合设计、BOX设计。现仅就这2个设计进行举例说明。 设:y=f(x,x2,x)≈a+bx+…+cx,+d2+…+ex2+ +fx2+…+gx2X3
2 验所得试验数据来估计 Ey f x x = ( 1 , , p ) (由部分来说明全体)。 哪么用什么样的模型来估计 Ey f x x = ( 1 , , p ) 呢?在数学分析上已有麦 克劳林或泰勒展开式即: ( ) ( ) ( ) ( ) ' 2 0 " 0 0 1! 2! f f f x f x x + + + 一般都能满足(收敛),又生物科学领域变量间的特点,因此用 ( ) 2 2 1 1 1 , , Ey f x x a bx cx dx ex = + + + + + + + + p p p 1 2 1 p p fx x gx x + − 模型。 综上所述:试验得试验点: ( x x y x x y 11 1 1 1 , , , , , , p n pn n ) ( ) 估计出 ( ) 2 2 1 1 1 , , Ey f x x a bx cx dx ex = + + + + + + + + p p p 1 2 1 p p fx x gx x + − 的系数 a b, , ,如果可用(检验),则 1 , p x x y 与 的关 系就全面掌握了。 3. 响应面分析的试验设计(DOE——Design of Exprement)—用 Design-Expert7 软件 试验点 ( x x y x x y 11 1 1 1 , , ? , , , , ? p n pn n ) ( ) 选择哪些点才能比较科 学地反映客观实际呢(包括试验次数要尽可能少、自变量间正交等)?这就是称 为试验设计研究。响应面分析的试验设计有: 中心组合设计(Central Composite Design—CCD,二次正交旋转组合设计); BOX 设计(Box-Behnken 设计); D-optimal设计(2次饱和D—最优设计) 均匀设计; 田口设计; …。 常用的是中心复合设计、BOX 设计。现仅就这 2 个设计进行举例说明。 设: ( ) 2 2 1 2 3 1 3 1 3 Ey f x x x a bx cx dx ex = + + + + + + + , , 1 2 2 3 + + + fx x gx x
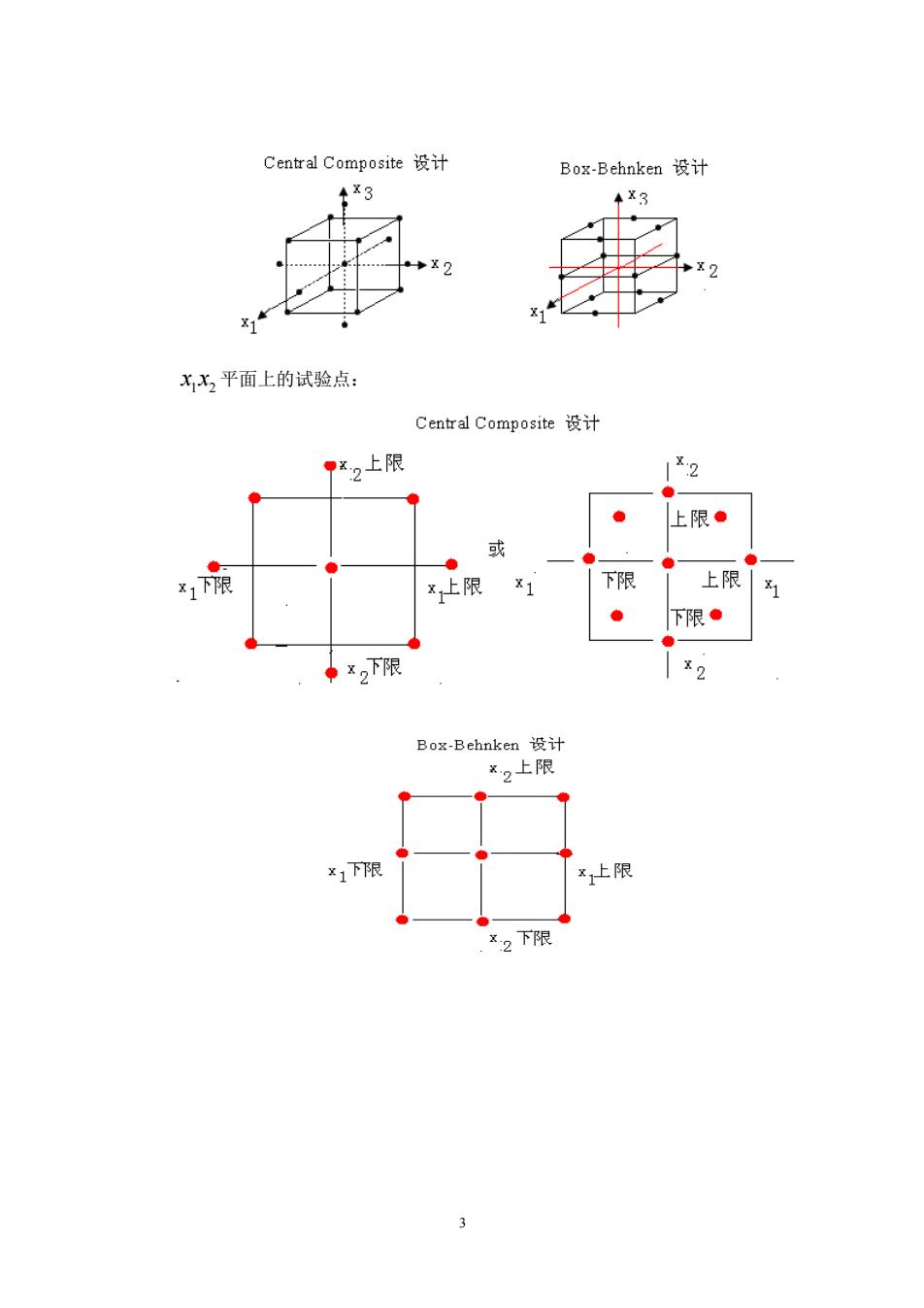
Central Composite设计 Box-Behnken设计 4x3 +x3 ¥2 Xx2平面上的试验点: Central Composite设计 72上限 ● 上限● 或 ● X1下限 限 4y 下限 上限 1 下限● x2下限 Box-Behnken设计 ×2上限 x1下限 ×上限 x:2下限 3
3 1 2 xx 平面上的试验点:
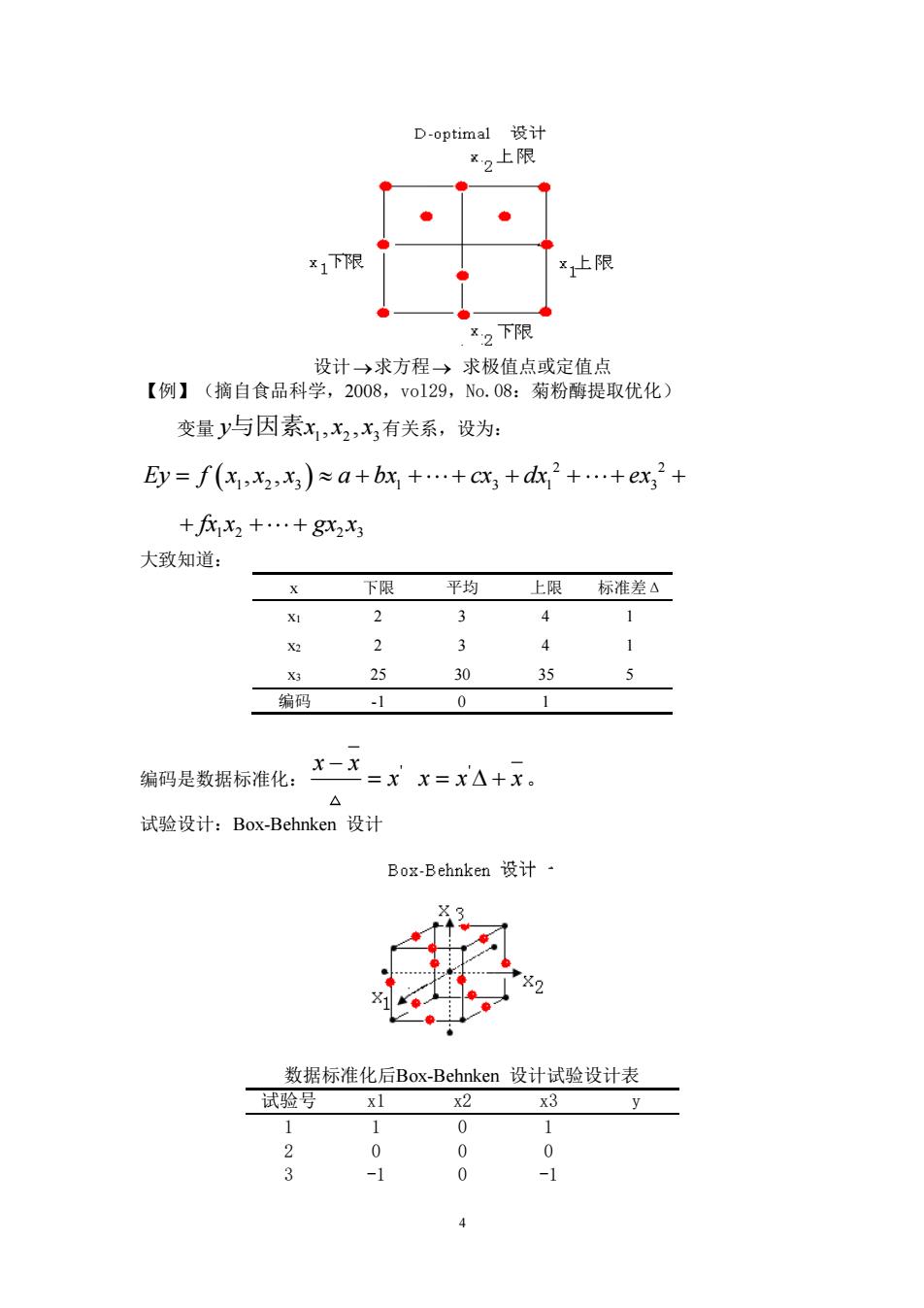
D-optimal设计 ×2上限 1下限 上限 *2下限 设计→求方程)求极值点或定值点 【例】(摘自食品科学,2008,vo129,No.08:菊粉酶提取优化) 变量y与因素x,x2,x3有关系,设为: y=f(x,2,x3)≈a+bx+…+cx3+d2+…+x2+ +x2+…+8x2X3 大致知道: 下限 平均 上限 标准差△ X1 2 3 4 1 X2 2 J 1 X3 25 30 35 5 编码 -1 0 1 x-x 编码是数据标准化: =xx=x△+x。 △ 试验设计:Box-Behnken设计 Box-Behnken设计· 1 数据标准化后Box-Behnken设计试验设计表 试验号 xl x2 X3 1 1 0 1 2 0 0 0 -1 0 -1
4 设计 → 求方程 → 求极值点或定值点 【例】(摘自食品科学,2008,vol29,No.08:菊粉酶提取优化) 变量 1 2 3 y x x x 与因素 , , 有关系,设为: ( ) 2 2 1 2 3 1 3 1 3 Ey f x x x a bx cx dx ex = + + + + + + + , , 1 2 2 3 + + + fx x gx x 大致知道: x 下限 平均 上限 标准差Δ x1 2 3 4 1 x2 2 3 4 1 x3 25 30 35 5 编码 -1 0 1 编码是数据标准化: x x ' ' x x x x − = = + 。 试验设计:Box-Behnken 设计 数据标准化后Box-Behnken 设计试验设计表 试验号 x1 x2 x3 y 1 1 0 1 2 0 0 0 3 -1 0 -1

4 1 1 0 5 1 0 -1 6 0 -1 1 1 1 -1 0 8 0 0 0 9 -1 -1 0 10 0 0 0 11 0 0 0 12 -1 0 1 13 0 -1 -1 14 0 1 1 15 -1 1 0 16 0 0 0 17 0 1 -1 Box-Behnken设计试验设计表 试验号 xl x2 x3 1 4 3 35 2 J 30 3 2 3 25 4 4 4 30 × 3 25 6 3 2 35 > 2 30 8 3 3 30 9 2 2 30 10 3 3 30 11 3 30 12 2 3 35 13 3 2 25 14 3 4 35 15 3 ¥ 30 16 3 3 30 17 3 4 25 数据标准化后Central Composite设计试验设计表 试验号 xl x2 X3 1 -1 -1 2 0 -1.682 0 3 -1 1 1 4 -1.682 0 0 5 0 1.682 0
5 4 1 1 0 5 1 0 -1 6 0 -1 1 7 1 -1 0 8 0 0 0 9 -1 -1 0 10 0 0 0 11 0 0 0 12 -1 0 1 13 0 -1 -1 14 0 1 1 15 -1 1 0 16 0 0 0 17 0 1 -1 Box-Behnken 设计试验设计表 试验号 x1 x2 x3 y 1 4 3 35 2 3 3 30 3 2 3 25 4 4 4 30 5 4 3 25 6 3 2 35 7 4 2 30 8 3 3 30 9 2 2 30 10 3 3 30 11 3 3 30 12 2 3 35 13 3 2 25 14 3 4 35 15 2 4 30 16 3 3 30 17 3 4 25 数据标准化后Central Composite 设计试验设计表 试验号 x1 x2 x3 y 1 -1 -1 1 2 0 -1.682 0 3 -1 1 1 4 -1.682 0 0 5 0 1.682 0

6 1 1 -1 7 -1 -1 -1 8 0 0 0 9 0 0 1.682 10 -1 1 -1 11 -1 1 12 1.682 0 0 13 0 0 -1.682 14 0 0 0 15 1 -1 -1 16 0 0 0 17 0 0 0 18 1 1 1 19 0 0 0 20 0 0 0 x=1.682→x1=x△1+x=1.682×1+3=4.682 x3=-1.682→x3=x3△3+x3=-1.682×5+30=21.59。 数据标准化后D-optimali设计试验设计表 试验号 x2 y 1 0.5 0.5 2 -1 1 3 1 0 4 1 1 5 0 1 6 0 -1 7 1 0 8 0 -0.5 9 1 -1 10 -0.5 0.5 11 -1 0 12 -1 13 -1 -1 14 1 1 15 -1 1 16 -1 -1 4.响应面分析一用Design-Expert7 6
6 6 1 1 -1 7 -1 -1 -1 8 0 0 0 9 0 0 1.682 10 -1 1 -1 11 1 -1 1 12 1.682 0 0 13 0 0 -1.682 14 0 0 0 15 1 -1 -1 16 0 0 0 17 0 0 0 18 1 1 1 19 0 0 0 20 0 0 0 ' ' 1 1 1 1 1 x x x x = → = + = + = 1.682 1.682 1 3 4.682 … ' ' 3 3 3 3 3 x x x x = − → = + = − + = 1.682 1.682 5 30 21.59。 数据标准化后D-optimal设计试验设计表 试验号 x1 x2 y 1 0.5 0.5 2 -1 1 3 1 0 4 1 1 5 0 1 6 0 -1 7 1 0 8 0 -0.5 9 1 -1 10 -0.5 0.5 11 -1 0 12 1 -1 13 -1 -1 14 1 1 15 -1 1 16 -1 -1 4. 响应面分析—用Design-Expert7
【例】(摘自食品科学,2008,vo129,No.08:菊粉酶提取优化) 变量y与因素x1,x2,x3有关系,设为: Ey=f(x,x2,x3)≈a+bx+…+cx3+dk2+…+ex32+ +fx2+…+gr2X3 希望知道在下表范围的响应面: 表1中心组合试验设计因素水平及编码 下限 平均 标准差 上限 4 1.318 2 3 4.682 1 X2 1.318 2 4.682 X3 21.59 25 30 35 38.41 5 编码 -1.682 -1 0 1 1.682 编码是数据标准化: x-x =Xx=x△+x。 采用Central Composite试验设计 回响应面分折讲义.d0 :文件)编辑)视 Windows Catalog @海2007专业版 键入需要帮助的问 03日引% Windows Update visagesoft 四B卫,小言嘉拒 通打开0ffic。文档 回4282 鱼金山词霸2003 国新键0fice文档 国金山快译2005 32343638d0424 ACDSee MathType 5 面STATISTICA8.0Demo Administ 画F1 ashGet Microsoft Office S-PLUS 7.0 Real 国Stat-2:e Design-Expert 7.1.6 Trial Internet Explore 回WinRAR 回Minitab Solutions Design-Expert 7.1.6 Trial @M7 Uninstall Design-Expert 7.: 电子廊件 回暴风影音 回附件 画PDP2Word 国绿色软件 VeryPDF PDF2Word v3.0 鱼启动 Foxit PDF Editor ,台理取值,求得使 >
7 【例】(摘自食品科学,2008,vol29,No.08:菊粉酶提取优化) 变量 1 2 3 y x x x 与因素 , , 有关系,设为: ( ) 2 2 1 2 3 1 3 1 3 Ey f x x x a bx cx dx ex = + + + + + + + , , 1 2 2 3 + + + fx x gx x 希望知道在下表范围的响应面: 表1 中心组合试验设计因素水平及编码 x 下限 平均 上限 标准差 Δ x1 1.318 2 3 4 4.682 1 x2 1.318 2 3 4 4.682 1 x3 21.59 25 30 35 38.41 5 编码 -1.682 -1 0 1 1.682 编码是数据标准化: x x ' ' x x x x − = = + 。 采用Central Composite试验设计
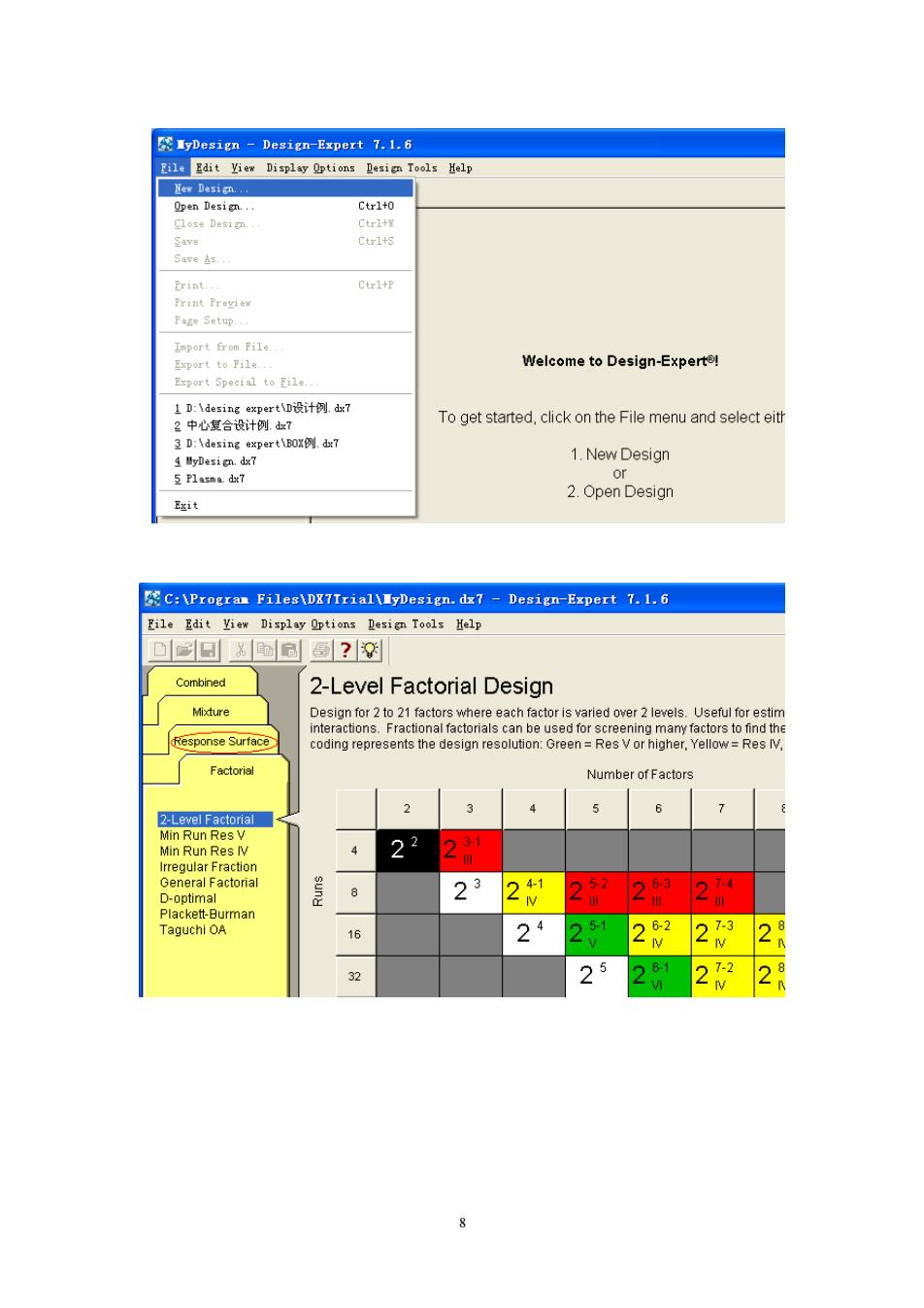
IyDesign -Design-Expert 7.1.6 Edit View Display Options Design Tools Help New Desicn... Open Design... Ctr1+0 Close Design. Ctrl+W Save Ctri+S Save As Print.. Ctrl+P Print Preview Page Setup.. Import from File Export to File... Welcome to Design-Experte! Export Special to File. 1D:\desing expert\D设计例.dx7 2中心复合设计例.7 To get started,click on the File menu and select eith 3 D:\desing expert\BOX.dx7 4 MyDesign.dx7 1.New Design 5 Plasma.dx7 or 2.Open Design B巡it C:\Progran Files\DX7Trial\lyDesign.dx7 -Design-Expert 7.1.6 Eile Edit View Display Options Design Tools Help 口回国圆?到 Combined 2-Level Factorial Design Mixture Design for 2 to 21 factors where each factor is varied over 2 levels.Useful for estim interactions.Fractional factorials can be used for screening many factors to find the Response Surface coding represents the design resolution:Green Res V or higher,Yellow=Res IV, Factorial Number of Factors 2 3 5 7 2-Level Factorial Min Run Res V Min Run Res IV 22 231 Irregular Fraction General Factorial 8 23 241 52 263 D74 D-optimal Plackett-Burman Taguchi OA 16 24 261 6-2 7-3 28 6-1 7-2 32 5 8 8
8
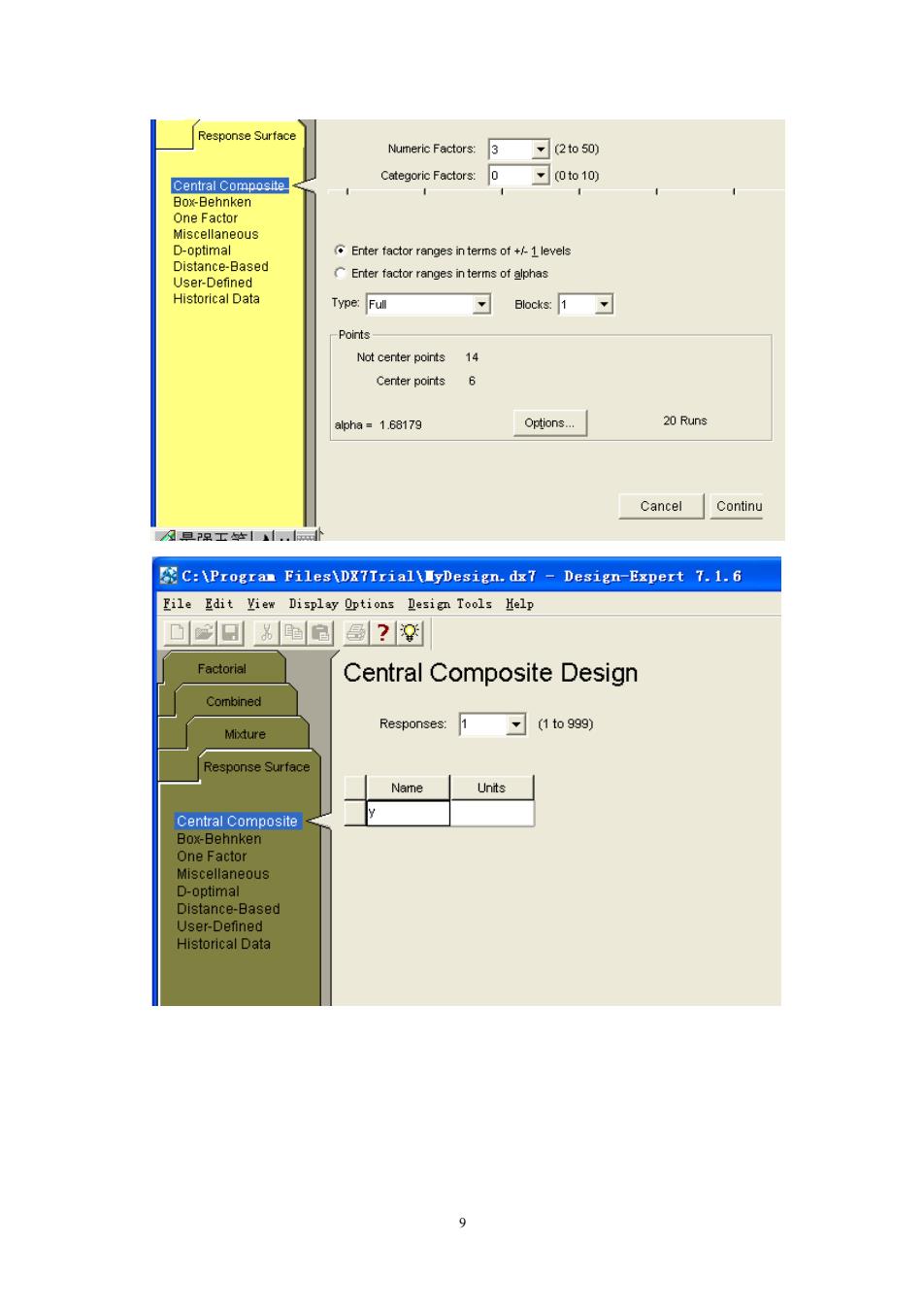
Response Surface Numeric Factors: 3 -(2to50) Categoric Factors: 0 0to10) Central Composite Box-Behnken One Factor Miscellaneous D-optimal Enter factor ranges in terms of +/-1 levels Distance-Based CEnter factor ranges in terms of alphas User-Defined Historical Data Type:Full Blocks:1 -Points Not center points 14 Center points alpha=1.68179 Options... 20 Runs Cancel Continu 旦2早工.,N C:\Progran Files\DX7Irial\yDesign.dx7 Design-Expert 7.1.6 File Edit View Display Options Design Tools Help 口回幽 曼?窖 Factorial Central Composite Design Combined Mixture Responses: 1to999) Response Surface Name Units Central Composite Box-Behnken One Factor Miscellaneous D-optimal Distance-Based User-Defined Historical Data
9