
第三章 平均数、标准差 与变异系数 第一节平均数 上一张下一张主页退出
第三章 平均数、标准差 与变异系数 第一节 平均数 上一张 下一张 主 页 退 出

平均数是统计学中最常用的统计量,用来表明 资料中各观测值相对集中较多的中心位置。平均数 主要包括有: 算术平均数(arithmetic mean) 中位数(median) 众数(mode) 几何平均数(geometric mean) 调和平均数(harmonic mean) 上一张下一张主页退出
平均数是统计学中最常用的统计量,用来表明 资料中各观测值相对集中较多的中心位置。平均数 主要包括有: 算术平均数(arithmetic mean) 中位数(median) 众数(mode) 几何平均数(geometric mean) 调和平均数(harmonic mean) 上一张下一张主 页 退 出

一、算术平均数 算术平均数是指资料中各观测值的总和除 以观测值个数所得的商,简称平均数或均数 记为。 算术平均数可根据样本大小及分组情况而 采用直接法或加权法计算。 (一)直接法 主要用于样本含量n≤30以下、未经分组 资料平均数的计算。 上一张下一张主页退出
一、算术平均数 算术平均数是指资料中各观测值的总和除 以观测值个数所得的商,简称平均数或均数, 记为。 算术平均数可根据样本大小及分组情况而 采用直接法或加权法计算。 (一)直接法 主要用于样本含量n≤30以下、未经分组 资料平均数的计算。 上一张 下一张 主 页 退 出

设某一资料包含n个观测值:X1、X2、.、Xn, 则样本平均数可通过下式计算: x- X1+x2+…+n i=1 (3-1) n n 其中,Σ为总和符号;x 表示从第一个观测 值X1累加到第n个观测值x。当 在意义上已明 确时,可简写为X, (3-1)式可改写为: x= 上一张下一张主页退出
设某一资料包含n个观测值: x1、x2、…、xn, 则样本平均数可通过下式计算: (3-1) 其中,Σ为总和符号; 表示从第一个观测 值x1累加到第n个观测值xn。当 在意义上已明 确时,可简写为Σx,(3-1)式可改写为: n x n x x x x n i i n = = + + + = 1 2 1 = n i i x 1 n x x = 上一张 下一张 主 页 退 出

【例3.1】某种公牛站测得10头成年公牛的体 重分别为500、520、535、560、585、600、 480、510、505、490(kg),求其平均数。 由于 Σx=500+520+535+560+58 +600+480+510+505+49 =5285, n=10 上一张下一张主页退出
【例3.1】 某种公牛站测得10头成年公牛的体 重分别为500、520、535、560、585、600、 480、510、505、490(kg),求其平均数。 由于 Σx=500+520+535+560+58 +600+480+510+505+49 =5285, n=10 上一张 下一张 主 页 退 出

得: = 5285 528.5kg n 10 即10头种公牛平均体重为528.5kg。 (二)加权法 对于样本含量n≥30以上且已分组的资 料,可以在次数分布表的基础上采用加权法计 算平均数,计算公式为: 天=+出++f&=兰 ∑尔 (3-2) f+f2+…+f i=l 上一张下一张主页退出
得: 即10头种公牛平均体重为528.5 kg。 (二)加权法 对于样本含量 n≥30 以上且已分组的资 料,可以在次数分布表的基础上采用加权法计 算平均数,计算公式为: (3-2) 528.5(kg) 10 ∑ 5285 = = = n x x = = + + + + + + = = = f f x f f x f f f f x f x f x x k i i k i i i k k k 1 1 1 2 1 1 2 2 上一张 下一张 主 页 退 出

式中:x;一第组的组中值; f一第组的次数; 飞一分组数 第组的次数f是权衡第组组中值x在资料 中所占比重大小的数量,因此将f,称为是x的 “权”,加权法也由此而得名。 【例3.2】 将100头长白母猪的仔猪一月 窝重(单位:kg)资料整理成次数分布表如 下,求其加权数平均数。 上一张下一张主页退出
式中: —第i组的组中值; —第i组的次数; —分组数 第i组的次数fi是权衡第i组组中值xi在资料 中所占比重大小的数量,因此将fi 称为是xi的 “权”,加权法也由此而得名。 【例3.2】 将100头长白母猪的仔猪一月 窝重(单位:kg)资料整理成次数分布表如 下,求其加权数平均数。 i x i f k 上一张 下一张 主 页 退 出
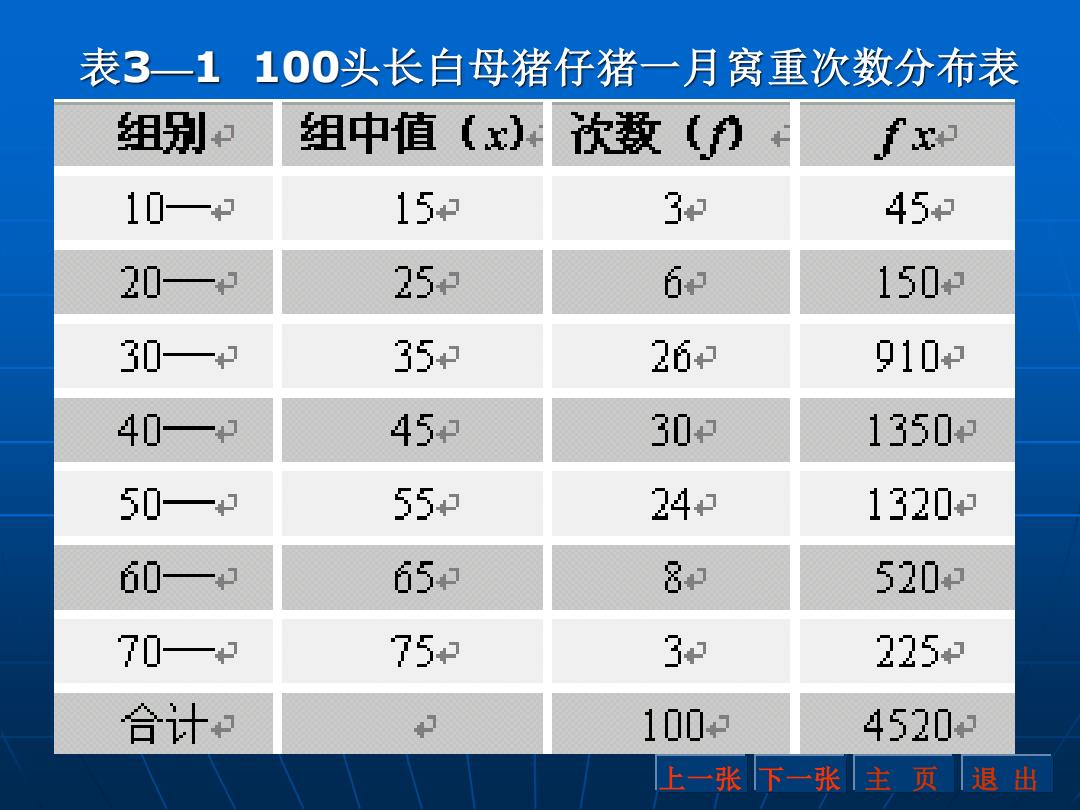
表3一1100头长白母猪仔猪一月窝重次数分布表 组别 组中值(x次数(力+ f 10- 15 3 45 20—1 25 6 150 30一1 35 26和 910 40一2 45 30 1350 50一4 55 24 1320 60一中 65e 8和 520 70一 75 3和 225 合计 100+ 4520 上一张下一张主页退出
表3—1 100头长白母猪仔猪一月窝重次数分布表 上一张 下一张 主 页 退 出

利用(3一2)式得: Σ 4520 x= f 45.2(kg 100 即这100头长白母猪仔猪一月龄平均窝重 为45.2kg。 计算若干个来自同一总体的样本平均数的 平均数时,如果样本含量不等,也应采用加权 法计算。 上一张下一张主页退出
利用(3—2)式得: 即这100头长白母猪仔猪一月龄平均窝重 为45.2kg。 计算若干个来自同一总体的样本平均数的 平均数时,如果样本含量不等,也应采用加权 法计算。 45.2( ) 100 4520 k g f f x x = = = 上一张 下一张 主 页 退 出

【例3.3 某牛群有黑白花奶牛1500 头,其平均体重为750kg,而另一牛群有黑 白花奶牛1200头,平均体重为725kg,如 果将这两个牛群混合在一起,其混合后平均体 重为多少? 此例两个牛群所包含的牛的头数不等,要 计算两个牛群混合后的平均体重,应以两个牛 群牛的头数为权,求两个牛群平均体重的加权 平均数,即 上一张下一张主页退出
【例3.3】 某牛群有黑白花奶牛 1500 头,其平均体重为750 kg ,而另一牛群有黑 白花奶牛1200头,平均体重为725 kg,如 果将这两个牛群混合在一起,其混合后平均体 重为多少? 此例两个牛群所包含的牛的头数不等,要 计算两个牛群混合后的平均体重,应以两个牛 群牛的头数为权,求两个牛群平均体重的加权 平均数,即 上一张 下一张 主 页 退 出