
第七章混料试验设计与分析 在工农业生产和科学研究中,时常会遇到配方配比问题。比如,将若干种成分 (component),按百分比混合在一起形成混料,如饲料由A、B、C三种原料组成,三种原 料各占百分比是多少动物生长更有利,又例如,某种不锈钢由铁、镍、铜和铬四种元素 组成,我们想知道每种元素所占百分比与抗拉强度的数量关系。这些都是混料问题。对 于上述问题,要进行试验,探索混料各成分的百分比与试验研究指标之间的关系,进而 来回答上述问题。 混料设计(mixture design)就是要合理地选择少量的试验点,通过不同百分比成分的 混料试验,得到试验指标与混料中各种成分所占百分比的回归方程,通过回归方程和其 图形一响应曲面给出统计结论。 自从H.Scheffe1958年提出单纯形格子设计以来,混料回归设计的理论和它的应 用都有很大发展。混料设计在工业、农业和科学试验中都得到广泛的应用。汽油混合物、 混凝土、食品、饲料、医药等产品的研发上都会遇到混料设计问题。本文着重介绍 H.Scheffe提出的混料的单纯形格子设计和单纯形重心设计。 第一节混料设计模型 设p种成分的混料中,p种成分各占的百分比是,…,x。,其对应的试验指 标是y,表示为(x,…,xp,y),其中 2x=1,0≤x≤1,i=1,…p 如果x,…,xpy有关系,设为E(y)=(,…,x) 现要估计它,用多项式去估计,可以用一次、二次、高次多项式进行估计, 一般用二次多项式去估计,如果估计达不到要求,则用高次多项式进行估计。 (1)用二次多项式去估计,即设E(y)=∫(x,…,xn)的估计是: =bx,+bop (7-1) i<i 现以p=3进行说明。三元二次多项式是 =6+∑bx+2b,xx+2bx (7-2) i<j 由x+x2+x3=1可得 -176-
- 176 - 第七章 混料试验设计与分析 在工农业生产和科学研究中,时常会遇到配方配比问题。比如,将若干种成分 (component)按百分比混合在一起形成混料,如饲料由 A、B、C 三种原料组成,三种原 料各占百分比是多少动物生长更有利,又例如,某种不锈钢由铁、镍、铜和铬四种元素 组成,我们想知道每种元素所占百分比与抗拉强度的数量关系。这些都是混料问题。对 于上述问题,要进行试验,探索混料各成分的百分比与试验研究指标之间的关系,进而 来回答上述问题。 混料设计(mixture design)就是要合理地选择少量的试验点,通过不同百分比成分的 混料试验,得到试验指标与混料中各种成分所占百分比的回归方程,通过回归方程和其 图形-响应曲面给出统计结论。 自从 H.Scheffe 1958 年提出单纯形格子设计以来,混料回归设计的理论和它的应 用都有很大发展。混料设计在工业、农业和科学试验中都得到广泛的应用。汽油混合物、 混凝土、食品、饲料、医药等产品的研发上都会遇到混料设计问题。本文着重介绍 H.Scheffe 提出的混料的单纯形格子设计和单纯形重心设计。 第一节 混料设计模型 设 p 种成分的混料中,p 种成分各占的百分比是 1 , , p x x ,其对应的试验指 标是 y ,表示为( 1 , , p x x ,y ),其中 1 1 p i i x = = , 0≤xi≤1,i=1,…,p 如果 1 , , p x x y 有关系,设为 E y f x x ( ) = ( 1 , , p ) 现要估计它,用多项式去估计,可以用一次、二次、高次多项式进行估计, 一般用二次多项式去估计,如果估计达不到要求,则用高次多项式进行估计。 (1)用二次多项式去估计,即设 E y f x x ( ) = ( 1 , , p ) 的估计是: 1 ˆ p p i i ij i j i i j y b x b x x = = + (7-1) 现以 p = 3 进行说明。三元二次多项式是 3 3 3 2 0 1 1 ˆ i i ij i j ii i i i j i y b b x b x x b x = = = + + + (7-2) 由 x1 + x2 + x3 =1 可得

bo box:box2 +box3 x=x(1-x3-x3)=x1-xx2-xx3 X2=X2-XX2-x2X3 x=X3-XX3-X2X3 将其代入回归方程(7-2),加以整理可得 =+∑xx (7-3) i0时,这种非线性混合关系是协调的: 而当b,<0时,则是对抗的。bx,xx也与bxx,一样。 目前,混料设计的方法已有多种,除了前面提到的单纯形格子设计,单纯形重心设 计外、有下界约束的混料设计、轴设计、凸多面体设计、C0x混料设计、混料均匀设计 等。本书只重点介绍单纯形格子设计和单纯形重心设计两种常用的设计方法。 第二节单纯形格子设计与统计分析 单纯形格子设计(simplex lattice design)是混料设计中最先出现的、最基本的一种设 计方法。 {P,d单纯形格子设计,试验点(X,,X)的选择是各成分X,在混料中所占百 分比 0a'a1,1=1,2,p 12 x=0 结合上x=1确定所有试验点。 al 如3,2单纯形格子设计,试验点(6,),=0,1,1=123, x1+x2+x3=1,x,0,i=1,2,3,所以试验点是 (LO.0)(C.L.O).o.)(--0.-o. 用图形表示 -177-
- 177 - ( ) 0 0 1 0 2 0 3 2 1 1 2 3 1 1 2 1 3 2 2 2 1 2 2 3 2 3 3 1 3 2 3 1 b b x b x b x x x x x x x x x x x x x x x x x x x x x x = + + = − − = − − = − − = − − 将其代入回归方程(7-2),加以整理可得 3 3 1 ˆ i i ij i j i i j y b x b x x = = + (7-3) (2)用一次多项式去估计,即设 E y f x x ( ) = ( 1 , , p ) 的估计是 = = p i i i y b x 1 ˆ (3)用三次多项式去估计,即设 E y f x x ( ) = ( 1 , , p ) 的估计是 1 ˆ ( ) p p p p i i ij i j ij i j i j ijk i j k i i j i j i j k y b x b x x r x x x x b x x x = = + + − + 或者是 1 ˆ p p p i i ij i j ijk i j k i i j i j k y b x b x x b x x x = = + + 用 {p,d} 表示 p 个成分 d 次多项式混料设计。试验点 ( x x 1 , , p ) 由 {p,d} 确定。 经试验所求回归方程可用,则可利用回归方程求出最大值点或最小值点、定值点等。需 要指出的是,以上回归方程中 ij i j b x x ,不能单纯理解为 i x 与 j x 的交互作用,它们只是表 示一种非线性混合的关系。Scheffe 认为,当 bij 0 时,这种非线性混合关系是协调的; 而当 bij 0 时,则是对抗的。 ijk i j k b x x x 也与 ij i j b x x 一样。 目前,混料设计的方法已有多种,除了前面提到的单纯形格子设计,单纯形重心设 计外、有下界约束的混料设计、轴设计、凸多面体设计、Cox 混料设计、混料均匀设计 等。本书只重点介绍单纯形格子设计和单纯形重心设计两种常用的设计方法。 第二节 单纯形格子设计与统计分析 单纯形格子设计(simplex lattice design)是混料设计中最先出现的、最基本的一种设 计方法。 {p,d} 单纯形格子设计,试验点 (x x 1 , , p ) 的选择是各成分 i x 在混料中所占百 分比 0 , i x i p = 1 2 , , , 1 , = 1,2, d d 结合 1 1 p i i x = = 确定所有试验点。 如{3,2}单纯形格子设计,试验点 ( 1 2 3 ) 1 , , 0, ,1 1,2,3 2 i x x x x i , = = , , 1 2 3 1 , 0 , 1,2,3 i x x x x i + + = = ≥ ,所以试验点是 ( )( )( ) 1 1 1 1 1 1 1,0,0 0,1,0 0,0,1 , ,0 ,0, 0, , 2 2 2 2 2 2 用图形表示

(0,0,1) x1+x2+5=1 (0,0,1) 丙十2+为=1 -X2 (0,1,0) (1,0,0) (0,1,0) 〔1,0,0) 图7-1单纯形格子设计试验点 图中三角形是x+x2+x=1,x,≥0,i=1,2,3的图形,黑心点表示试验点。图 中,3个顶点表示单一成分的混料,3条边上的点表示两种成分的混料,而三角形内的 点则表示三种成分的混料。 {P,{p,2{P,3}的试验点见表7-1~表7-3 表7-1p,1)单纯形格子设计表 试验号 x X2 … Xp 1 0 0 2… 0 0 0 0 1 表7-2{p,2;单纯形格子设计表 试验号 x X2 3 … Xp-1 子 1 1 0 0 0 0 2 0 0 0.… p 0 0 0 … 0 1 P+1 2 1-2 0 0 0 P+2 1-2 0 2 0 0 P+Ci 0 0 0 … 1-2 1 .178-
- 178 - 图 7-1 单纯形格子设计试验点 图中三角形是 1 2 3 1 0 1,2,3 i x x x x i + + = = , ≥ , 的图形,黑心点表示试验点。图 中,3 个顶点表示单一成分的混料,3 条边上的点表示两种成分的混料,而三角形内的 点则表示三种成分的混料。 p p p ,1 ,2 ,3 的试验点见表 7-1~表 7-3 表 7-1 {p ,1}单纯形格子设计表 试验号 1 x 2 x … p x 1 1 0 … 0 2 0 1 … 0 p 0 0 … 1 表 7-2 {p ,2}单纯形格子设计表 试验号 1 x 2 x 3 x … p−1 x p x 1 1 0 0 … 0 0 2 0 1 0 … 0 0 p 0 0 0 … 0 1 P+1 1 2 1 2 0 … 0 0 P+2 1 2 0 1 2 … 0 0 P+ 2 Cp 0 0 0 … 1 2 1 2

表7-3{p,3}单纯形格子设计表 试验号 X X2 X3 X … Xp-2 Xp-1 子 1 0 0 0 0 0 0 2 0 0 0 0 0 p 0 0 0 0 0 0 1 P+1 2 3 0 0 0 0 0 P+2 2 3 0 0 0 P43 0 0 0 0 P+4 0 0 0 1 2 3 3 1 p2 0 0 0 0 2-3 3 1 p2+1 3 0 0 0 0 p2+2 1-3 3 0 3 0 0 0 Pcp 0 1-3 1 0 0 3 3 下面用一实例来说明单纯形格子设计与试验结果的统计分析方法。 【例7-1】编制一个{3,2}单纯形格子设计的试验方案。 第一步,明确试验研究的目的,根据试验目的确定混料的各种成分(即试验因素)。 本例中混料成分的个数p=3。 第二步,按照专业知识的要求,根据各混料成分所占百分比的范围,确定出试验研 究范围内各成分百分比的最小值。用Z、Z2、Z,表示混料中3种成分的百分比,用a 42、4表示3种成分百分比的最小值。本设计就是要在条件 0≤4≤Z≤1,=1,2,3 Z+Z2+Z3=1 的限制下选择试验点进行试验。根据混料设计的特点,各混料成分百分比的最小值还应 满足条件 a<1 本例假设a1=0.3,42=0,43=0。 第三步,先从专业知识的角度确定需要估计的回归方程的次数d,然后依据混料成 分的个数p和回归方程的次数d山,选择适当的单纯形格子设计表。本例d=2。于是选 择{3,2}单纯形格子设计表,见表7-4。 表7-4{3,2}单纯形格子设计试验方案和试验结果 试验号 试验设计 试验方案 (处理) 女 古 X3 Z Z Z 试验指标 1 1 0 0 1 0 0 5.27 2 0 0 0.3 0.7 0 6.74 0 0 0.3 0 0.7 6.92 4 1/2 1/2 0 0.65 0.35 0 6.34 J 1/2 0 1/2 0.65 0 0.35 6.64 6 0 1/2 12 0.3 0.35 0.35 6.94 -179-
- 179 - 表 7-3 {p ,3}单纯形格子设计表 试验号 1 x 2 x 3 x 4 x … p −2 x p−1 x p x 1 1 0 0 0 … 0 0 0 2 0 1 0 0 … 0 0 0 p 0 0 0 0 … 0 0 1 P+1 3 1 3 2 0 0 … 0 0 0 P+2 3 2 3 1 0 0 … 0 0 0 P+3 3 1 0 3 2 0 … 0 0 0 P+4 3 2 0 3 1 0 … 0 0 0 P 2-1 0 0 0 0 … 0 3 1 3 2 P 2 0 0 0 0 … 0 3 2 3 1 P 2+1 3 1 3 1 3 1 0 … 0 0 0 P 2+2 3 1 3 1 0 3 1 … 0 0 0 P 2+ 3 p c 0 0 0 0 … 3 1 3 1 3 1 下面用一实例来说明单纯形格子设计与试验结果的统计分析方法。 【例 7-1】 编制一个{3,2}单纯形格子设计的试验方案。 第一步,明确试验研究的目的,根据试验目的确定混料的各种成分(即试验因素)。 本例中混料成分的个数 p = 3。 第二步,按照专业知识的要求,根据各混料成分所占百分比的范围,确定出试验研 究范围内各成分百分比的最小值。用 Z1 、Z2 、Z3 表示混料中 3 种成分的百分比,用 1 a 、 2 a 、 3 a 表示 3 种成分百分比的最小值。本设计就是要在条件 0≤ai≤Zi ≤1 , i=1,2,3 1 2 3 Z Z Z + + =1 的限制下选择试验点进行试验。根据混料设计的特点,各混料成分百分比的最小值还应 满足条件 1 1 = p i i a 本例假设 1 a = 0.3, 2 a = 0, 3 a = 0。 第三步,先从专业知识的角度确定需要估计的回归方程的次数 d,然后依据混料成 分的个数 p 和回归方程的次数 d,选择适当的单纯形格子设计表。本例 d = 2。于是选 择{3,2}单纯形格子设计表,见表 7-4。 表 7-4 {3,2}单纯形格子设计试验方案和试验结果 试验号 (处理) 试验设计 试验方案 试验指标 1 x 2 x 3 x Z1 Z2 Z3 1 1 0 0 1 0 0 5.27 2 0 1 0 0.3 0.7 0 6.74 3 0 0 1 0.3 0 0.7 6.92 4 1/2 1/2 0 0.65 0.35 0 6.34 5 1/2 0 1/2 0.65 0 0.35 6.64 6 0 1/2 1/2 0.3 0.35 0.35 6.94

第四步,确定各成分的实际百分比Z与编码值x之间的对应关系。其转换公式为 Z=(1->a)s +a j=l 将a=0.3,,=0,43=0代入,可得Z=0.7x1+0.3,Z=0.7x2,Z3=0.7x3 第五步,根据上式计算各试验点各成分的实际百分比,形成{3,2}单纯形格子设计 的试验方案,经试验得各点试验指标y,见表7-4。 第六步统计分析单纯形格子设计统计分析的主要内容是由试验结果计算回归方 程中的回归系数,从而得到确定的回归方程。 在单纯形格子设计中,回归方程的回归系数可以将表74试验点 (X,x2,x,y),i=1,…,6 分别代入回归方程求出,也可利用多元线性回归方程系数的求法,由试验点 (飞,x,x,X,X,xx,),i=1,…,6确定。本例的回归方程是 少=5.27x1+6.74x2+6.92x3+1.34x1x2+2.18x1x3+0.44x2x3(编码) (7-5) =5.27Z1+6.55Z2+6.29Z3+2.73ZZ2+4.45ZZ3+0.90Z2Z3 (实际)(7-6) 式(7-5)由编码试验点得出,式(7-6)由实际试验点得出。也可将灯=(21-0.3)/0.7, x2=z2/0.7,x3=23/0.7代入式(7-5)得 5.27(Z1-0.3),6.74226.92Z3 1.3432 0.71 ✉十 0.7 0.7 0.7 0.7 2.1833z (0.7 0.7 +044品 y2.26+7.53Z+8.81Z2+8.55Z3+2.73Z,Z2+4.45Z,乙3+0.9022Z3(实际) 方程(7-6)y的最大值是6.96,最大值点是 (Z1,Z2,Z3)=(0.34,0.15,0.51) 方程(7-5)y的最大值是6.96,最大值点(x,x2,x3)=(0.061,0.207,0.732)。由 Z=0.7x1+03,Z3=0.7x2,Z3=0.7x3变换成实际值是 (Z,Z2,Z3)=(0.70.061+0.3,0.7-0.207,0.7-0.732)=(0.34,0.15,0.51) 结论是:混料中的三种成分各占34%、15%、51%时,试验指标y最大,达到6.96。 y的等高线图7-2。 -180-
- 180 - 第四步,确定各成分的实际百分比 Zi 与编码值 i x 之间的对应关系。其转换公式为 1 (1 ) p i j i i j Z a x a = = − + 将 1 a = 0.3, 2 a = 0, 3 a = 0 代入,可得 Z1 = 0.7x1 + 0.3,Z2 = 0.7x2,Z3 = 0.7x3。 第五步,根据上式计算各试验点各成分的实际百分比,形成{3,2}单纯形格子设计 的试验方案,经试验得各点试验指标 y,见表 7-4。 第六步 统计分析 单纯形格子设计统计分析的主要内容是由试验结果计算回归方 程中的回归系数,从而得到确定的回归方程。 在单纯形格子设计中,回归方程的回归系数可以将表 7-4 试验点 ( x x x y i 1 2 3 i i i i , , , 1, ,6 ) , = 分别代入回归方程求出,也可利用多元线性回归方程系数的求法,由试验点 ( x x x x x x x x x y i 1 2 3 1 2 1 3 2 3 i i i i i i i i i i , , , , , , 1, ,6 ) , = 确定。本例的回归方程是: 1 2 3 1 2 1 3 2 3 y x x x x x x x x x ˆ = 5.27 +6.74 +6.92 +1.34 +2.18 +0.44 (编码) (7-5) 1 2 3 1 2 1 3 2 3 y = Z Z Z Z Z Z Z Z Z ˆ 5.27 + 6.55 + 6.29 + 2.73 + 4.45 + 0.90 (实际)(7-6) 式(7-5)由编码试验点得出,式(7-6)由实际试验点得出。也可将 x1=(z1- 0.3)/0.7, x2= z2 /0.7,x3= z3 /0.7 代入式(7-5)得 ( ) 1 2 1 2 3 1 3 2 3 y = + + ˆ -0.3 1.34 5.27 -0.3 6.74 6.92 0.7 + 0.7 0.7 0.7 0.7 -0.3 2.18 0.7 0.44 0.7 0.7 0.7 + + Z Z Z Z Z Z Z Z Z 1 2 3 1 2 1 3 2 3 y=-2.26+7.53 +8.81 +8.55 +2.73 ˆ Z Z Z ZZ +4.45 +0.90 ZZ ZZ (实际) 方程(7-6)y 的最大值是 6.96,最大值点是 (Z1, Z2, Z3)=(0.34,0.15 ,0.51) 方程(7-5)y 的最大值是 6.96,最大值点 ( x x x 1 2 3 , , 0.061,0.207,0.732 ) = ( ) 。由 Z1 = 0.7x1 + 0.3,Z2 = 0.7x2,Z3 = 0.7x3 变换成实际值是 (Z1, Z2, Z3)=(0.7·0.061 + 0.3,0.7·0.207,0.7·0.732)=(0.34,0.15,0.51) 结论是:混料中的三种成分各占 34%、15%、51%时,试验指标 y 最大,达到 6.96。 y 的等高线图 7-2

(1,0,0) 5.55217 5.83434 6.11651 6.39868 6.68085 (0,1,0) (0,0,1) 图7-2指标的等高线 说明: (1)最大值点可能有多个,根据实际选择:最值点可用Excel的规划求解算出: 利用多元线性回归方程求回归系数时,应不含常数项。 (2)成分下界。在{p,单纯形格子设计的混料试验中,绝大多数试验点混料的 成分中都有一个或几个成分为零。但在实际工作中,不等于零的成分是大多数,而且一 般情况下也不容许大多数成分为零,否则就失去了进行混料试验的意义。因此,【例7-1】 实质上属于有下界约束的混料设计,各混料成分的取值有最小值的限制。这就避免了混 料中部分成分为零的问题。 (3)方程的检验。通过混料试验的结果分析,可以得到相应的回归方程。该回归 方程是否能够描述所研究的整个混料系统,尚需进行检验。要完成检验,可能需要增加 试验点。 第三节单纯形重心设计与统计分析 在{p,d单纯形格子设计中,试验点各成分的编码值与回归方程的次数d有关, 为的整数倍。当d≥3时,在某些混料设计中部分试验点的非零成分的取值不相等, 这些不相等的成分对试验结果所起的作用不同,也直接对回归方程的估计产生不同程度 的影响。为了改进这一缺陷,Scheffe提出了单纯形重心设计(simplex centroid design)。 一、设计方法 对于{p,d}单纯形重心设计,试验点的组成如下: 以(1,0,0,,0)为代表的C。个点: 00..0 为代表的C个点: 00 为代表的C3个点: ,…,0,…0为代表的C个p点。注意试验次数等于回归方形 -181-
- 181 - 图 7-2 指标的等高线 说明: (1)最大值点可能有多个,根据实际选择;最值点可用 Excel 的规划求解算出; 利用多元线性回归方程求回归系数时,应不含常数项。 (2)成分下界。在 {p,d} 单纯形格子设计的混料试验中,绝大多数试验点混料的 成分中都有一个或几个成分为零。但在实际工作中,不等于零的成分是大多数,而且一 般情况下也不容许大多数成分为零,否则就失去了进行混料试验的意义。因此,【例 7-1】 实质上属于有下界约束的混料设计,各混料成分的取值有最小值的限制。这就避免了混 料中部分成分为零的问题。 (3)方程的检验。通过混料试验的结果分析,可以得到相应的回归方程。该回归 方程是否能够描述所研究的整个混料系统,尚需进行检验。要完成检验,可能需要增加 试验点。 第三节 单纯形重心设计与统计分析 在 {p,d} 单纯形格子设计中,试验点各成分的编码值与回归方程的次数 d 有关, 为 d 1 的整数倍。当 d ≥3 时,在某些混料设计中部分试验点的非零成分的取值不相等, 这些不相等的成分对试验结果所起的作用不同,也直接对回归方程的估计产生不同程度 的影响。为了改进这一缺陷,Scheffe 提出了单纯形重心设计(simplex centroid design)。 一、设计方法 对于 {p,d} 单纯形重心设计,试验点的组成如下: 以(1,0,0,…,0)为代表的 1 Cp 个点; 以 1 1, ,0,0, ,0 2 2 为代表的 2 Cp 个点; 以 111 , , ,0,0, ,0 333 为代表的 3 Cp 个点; …… 以 1 1 1 , , , ,0, ,0 d d d 为代表的 d Cp 个 p 点。(注意试验次数等于回归方程系数。)

表7-5、表7-6列出了、{3,3}、{4,3)单纯形重心设计编码表。 表7-5{3,3}单纯形重心设计编码表 试验号 X X2 0 0 2 0 0 3 0 0 1 4 1-2 2 0 5 0 1-2 6 0 1-2 1 1-3 1-3 表7-6{4,3}单纯形重心设计编码表 试验号 X2 X3 X4 1 1 0 0 0 0 0 0 3 0 0 1 0 4 0 0 0 5 1 0 0 6 1-2 0 7 1 0 0 1-2 8 0 1-2 1-2 0 9 0 2 0 10 0 1 1 11 1-3 1-3 0 12 1-3 1 3 13 0 1-5 14 {p,d}单纯形重心设计的回归方程为 =26x+,,+2xX++ bw…X i<j<k i<i<id 其需要计算的回归系数与试验次数相等。 二、统计分析 与单纯形格子设计一样,单纯形重心设计回归方程中回归系数的计算也很简便。 将试验点与试验指标y代入回归方程。如以(1,0,0,…,0)为代表的C。个试验 点各成分编码值及其相应的试验结果值y,代入回归方程,即可得到单一成分的回归系 b=y,等,也可利用多元线性回归方程系数的求法,由试验点 (,,…,Xx2,…,XxXh,…y)i=1,,n 确定。 -182-
- 182 - 表 7-5、表 7-6 列出了、{3,3}、{4,3}单纯形重心设计编码表。 表 7-5 {3,3}单纯形重心设计编码表 试验号 1 x 2 x 3 x 1 1 0 0 2 0 1 0 3 0 0 1 4 1 2 1 2 0 5 1 2 0 1 2 6 0 1 2 1 2 7 1 3 1 3 1 3 表 7-6 {4,3}单纯形重心设计编码表 试验号 1 x 2 x 3 x 4 x 1 1 0 0 0 2 0 1 0 0 3 0 0 1 0 4 0 0 0 1 5 1 2 1 2 0 0 6 1 2 0 1 2 0 7 1 2 0 0 1 2 8 0 1 2 1 2 0 9 0 1 2 0 1 2 10 0 0 1 2 1 2 11 1 3 1 3 1 3 0 12 1 3 1 3 0 1 3 13 1 3 0 1 3 1 3 14 0 1 3 1 3 1 3 {p,d} 单纯形重心设计的回归方程为 1 2 1 2 1 2 1 ˆ d d d p p p p i i ij i j ijk i j k i i i i i i i i j i j k i i i y b x b x x b x x x b x x x = = + + + + 其需要计算的回归系数与试验次数相等。 二、统计分析 与单纯形格子设计一样,单纯形重心设计回归方程中回归系数的计算也很简便。 将试验点与试验指标 y 代入回归方程。如以(1,0,0,…,0)为代表的 1 Cp 个试验 点各成分编码值及其相应的试验结果值 i y 代入回归方程,即可得到单一成分的回归系 i i b = y 等,也可利用多元线性回归方程系数的求法,由试验点 ( x x x x x x x y i n 1 2 1 2 1 2 i i i i i i di i , , , , , , 1, , ) = 确定

【例7-2】在某配合饲料生产中,有Z,、Z2、Z、Z,四种预混料,假定它们的 用量最小值分别为41=0.30,a2=0.16,a3=0.04,a4=0.20。试安排{4,3} 单纯形重心设计试验方案。 在{4,4}单纯形重心设计编码表(表7-7)中,选择前C+C+C=14号试验点 构成{4,3}单纯形重心设计的试验点,其设计编码见表7-7。 表7-7{4,3}单纯形重心设计试验方案和试验结果 试验号 试验设计(编码) 试验方案(实际) (处理) x X3 Z Z, Z, Z 试验指标 1 1 0 0 0 0.60 0.16 0.04 0.20 14.6 2 0 1 0 0 0.30 0.46 0.04 0.20 14.9 3 0 0 0 0.30 0.16 0.34 0.20 13.8 4 0 0 0 0.30 0.16 0.04 0.50 14.2 2 0 0 0.45 0.31 0.04 0.20 12.8 6 2 0 0 0.45 0.16 0.19 0.20 13.3 7 049 0.16 0.04 0.35 13.5 8 0 0.3 0.31 0.19 0.20 13.6 0.04 0.35 13.4 10 0 0.19 0.35 12.6 11 3 0.40 0.26 0.14 0.20 13.0 12 3 3 0.40 0.26 0.04 0.30 12.4 13 3 0 0.40 0.16 0.14 0.30 13.2 14 0 0.30 0.26 0.14 0.30 13.6 由乙,=1-2a,x+a(a≤z≤) 式可得各成分实际因素与编码因素之间的关 系为 Z1=0.3x1+0.30 Z2=0.32+0.16 Z3=0.3x+0.04 Z4=0.3x4+0.20 将各试验点编码值代入上式求得实际值,将编码值换为实际值即得到试验方案,见表 7-7。 按照【例7-2】编制的试验方案进行试验,结果见表7-7的最后一列。由各试验点 编码值与试验指标y得到用编码表示的回归方程 y=14.6r1+14.92+13.8x3+14.2x4-7.8x1x2-3.6x1x3-3.6x1x4-3.0xmx3-4.6x4 -5.6x3x4十4.5x1x2x3-10.5x1x2x4+11.4x13x4+20.7x2x4(编码) 将其转化成用实际因素表示的回归方程: y=-41.82+166.6721222-388.8912224+422.22z12324+766.67222324+64.13z +72.0222+133.64z3+61.31z4-15.56312-151.11z123+5.33z124-236.67222 +34.89-2z4-311.56z324(实际) 由各试验点实际值与试验指标y得到实际的回归方程: y=22.31z1+30.20z2+91.82z3+19.49z4-15.56a12-151.11z123+5.33z124 -236.67223+34.892224-311.56z324+166.67z12223-388.89z12224++422.22z12324 +766.67222324(实际) -183-
- 183 - 【例 7-2】 在某配合饲料生产中,有 Z1 、Z2 、Z3、 Z4 四种预混料,假定它们的 用量最小值分别为 a1 = 0.30,a2 = 0.16,a3 = 0.04,a4 = 0.20。试安排{4,3} 单纯形重心设计试验方案。 在{4,4}单纯形重心设计编码表(表 7-7)中,选择前 14 3 4 2 4 1 C4 + C +C = 号试验点 构成{4,3}单纯形重心设计的试验点,其设计编码见表 7-7。 表 7-7 {4,3}单纯形重心设计试验方案和试验结果 试验号 (处理) 试验设计(编码) 试验方案(实际) 试验指标 1 x 2 x 3 x 4 x Z1 Z2 Z3 Z4 1 1 0 0 0 0.60 0.16 0.04 0.20 14.6 2 0 1 0 0 0.30 0.46 0.04 0.20 14.9 3 0 0 1 0 0.30 0.16 0.34 0.20 13.8 4 0 0 0 1 0.30 0.16 0.04 0.50 14.2 5 1 2 1 2 0 0 0.45 0.31 0.04 0.20 12.8 6 1 2 0 1 2 0 0.45 0.16 0.19 0.20 13.3 7 1 2 0 0 1 2 0.45 0.16 0.04 0.35 13.5 8 0 1 2 1 2 0 0.30 0.31 0.19 0.20 13.6 9 0 1 2 0 1 2 0.30 0.31 0.04 0.35 13.4 10 0 0 1 2 1 2 0.30 0.16 0.19 0.35 12.6 11 1 3 1 3 1 3 0 0.40 0.26 0.14 0.20 13.0 12 1 3 1 3 0 1 3 0.40 0.26 0.04 0.30 12.4 13 1 3 0 1 3 1 3 0.40 0.16 0.14 0.30 13.2 14 0 1 3 1 3 1 3 0.30 0.26 0.14 0.30 13.6 由 ( ) 1 (1 ) 1 p i j i i i j Z a x a a = = − + Z 式可得各成分实际因素与编码因素之间的关 系为 Z1 = 0.3x1+0.30 Z2 = 0.3x2+0.16 Z3 = 0.3x3+0.04 Z4 = 0.3x4+0.20 将各试验点编码值代入上式求得实际值,将编码值换为实际值即得到试验方案,见表 7-7。 按照【例 7-2】编制的试验方案进行试验,结果见表 7-7 的最后一列。由各试验点 编码值与试验指标 y 得到用编码表示的回归方程 y ˆ = 14.6x1+14.9x2+13.8x3+14.2x4-7.8x1x2-3.6x1x3-3.6x1x4-3.0x2x3-4.6x2x4 -5.6x3x4+4.5x1x2x3-10.5x1x2x4+11.4x1x3x4+20.7x2x3x4(编码) 将其转化成用实际因素表示的回归方程: y ˆ = -41.82+166.67z1z2z3-388.89z1z2z4+422.22z1z3z4+766.67z2z3z4+64.13z1 + 72.02z2+133.64z3+61.31z4-15.56z1z2-151.11z1z3+5.33z1z4-236.67z2z3 +34.89z2z4-311.56z3z4(实际) 由各试验点实际值与试验指标 y 得到实际的回归方程: y ˆ = 22.31z1+30.20z2+91.82z3+19.49z4-15.56z1z2-151.11z1z3+5.33z1z4 -236.67 z2 z3+34.89 z2z4-311.56z3z4+166.67z1z2z3-388.89z1z2z4++422.22z1z3z4 +766.67z2z3z4(实际)
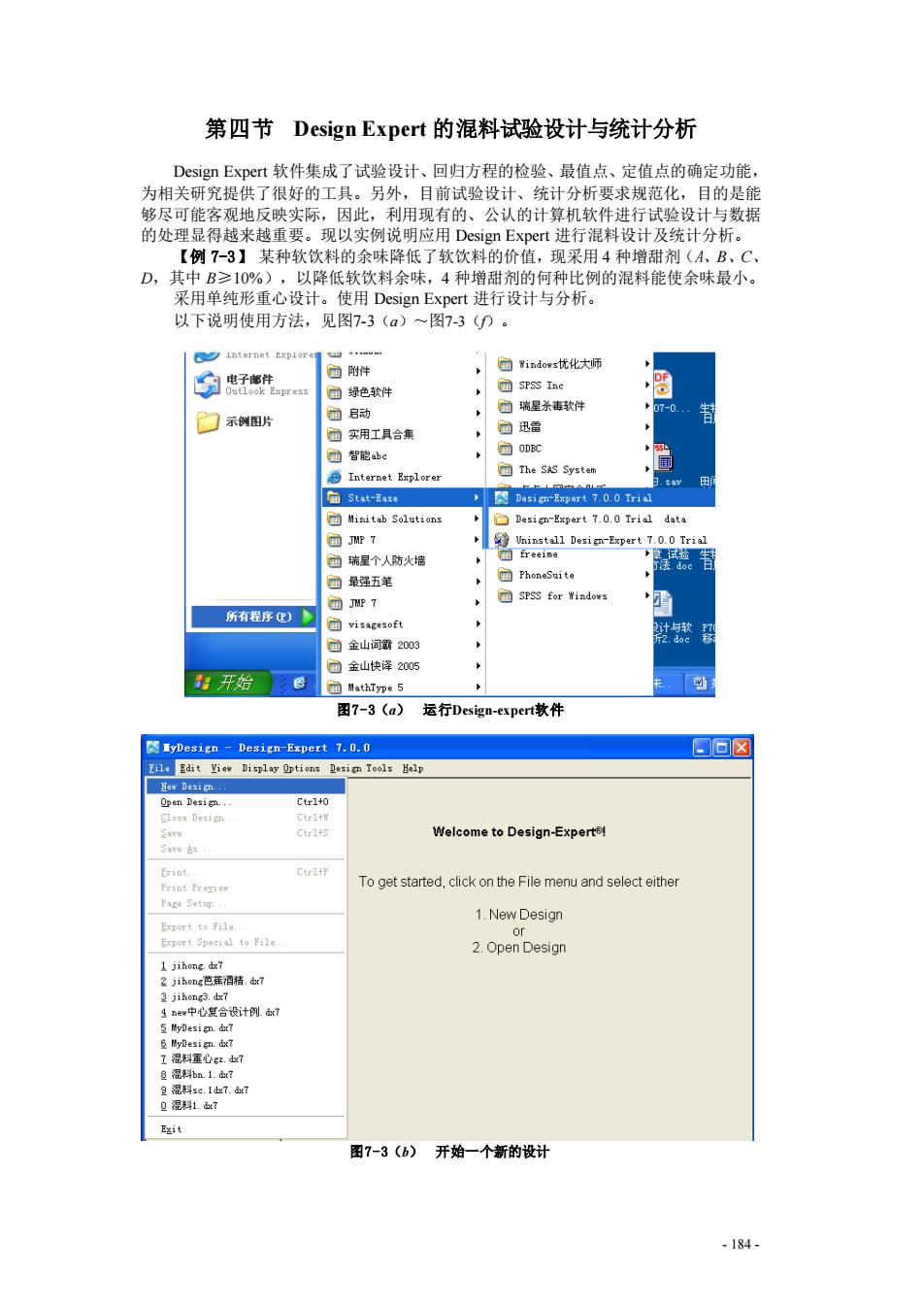
第四节Design Expert的混料试验设计与统计分析 Design Expert软件集成了试验设计、回归方程的检验、最值点、定值点的确定功能, 为相关研究提供了很好的工具。另外,目前试验设计、统计分析要求规范化,目的是能 够尽可能客观地反映实际,因此,利用现有的、公认的计算机软件进行试验设计与数据 的处理显得越来越重要。现以实例说明应用Design Expert进行混料设计及统计分析。 【例7-3】某种软饮料的余味降低了软饮料的价值,现采用4种增甜剂(A、B、C、 D,其中B≥10%),以降低软饮料余味,4种增甜剂的何种比例的混料能使余味最小。 采用单纯形重心设计。使用Design Expert进行设计与分析。 以下说明使用方法,见图7-3(a)~图7-3(f)。 internet Expiorem 匀电子生 面附伴 国Windowst忧化大师 回绿色软件 SPSS Ine Uut0 oK Expres写 回瑞星杀毒软件 门示例图片 园启动 血实用工具合集 @迅雷 智能abc 面ODEC ©The SAS System 国 Internet Explorer Stat-Ease Design-Expert 7.0.0 Trial Minitab Solutions D)Design-Expert 7.0.0 Trial data 鱼7 Uninstall Design-Expert 7.0.0 Trial 面瑞星个人防火墙 freeine @最强五笔 PhoneSuite 鱼JT ▣SPSS for Windows 所有程序) 回visag8soft 国金山词霸2003 鱼金山快译2005 开始 面MathType5 图7-3(a) 运行Design--expert软件 IyDesign-Design-Expert 7.0.0 日▣☒ Eil8里dit Viev Display Options卫esign Tools Help New Desien. Open Design... Ctr1+0 Close Design. Ctl+W Save Ctrl4S Welcome to Design-Expertel Sava年 Print.. Ctrl+P Print Preview To get started,click on the File menu and select either Page Setup. 1.New Design Export to Fila. or Export Special to File 2.Open Design 1 jihong.dx7 2 jihong芭蕉酒精.ds7 3 jihong3.dx7 4new中心复合设计例.dx7 5 MyDlesign.dx7 旦MyDesign.dx7 工混料重心g.dx7 8混料bn.1.x7 9混料sc.1d7.d7 Q混料1.d7 E继it 图7-3(b)开始一个新的设计 -184-
- 184 - 第四节 Design Expert 的混料试验设计与统计分析 Design Expert 软件集成了试验设计、回归方程的检验、最值点、定值点的确定功能, 为相关研究提供了很好的工具。另外,目前试验设计、统计分析要求规范化,目的是能 够尽可能客观地反映实际,因此,利用现有的、公认的计算机软件进行试验设计与数据 的处理显得越来越重要。现以实例说明应用 Design Expert 进行混料设计及统计分析。 【例 7-3】 某种软饮料的余味降低了软饮料的价值,现采用 4 种增甜剂(A、B、C、 D,其中 B≥10%),以降低软饮料余味,4 种增甜剂的何种比例的混料能使余味最小。 采用单纯形重心设计。使用 Design Expert 进行设计与分析。 以下说明使用方法,见图7-3(a)~图7-3(f)。 图7-3(a) 运行Design-expert软件 图7-3(b) 开始一个新的设计

图c:Documents and Settings\All Users\Documents\DX7 data\yDesign,dkT-Design--Expert-□▣☒ File Edit View Display Options Desien Tools Help Combined 2-Level Factorial Design Mixture 混料设计 3 where each factor is varied over 2 levels.Useful for estimating main effects and actorials 响应面设计 used for scree ning mary l ors to find the sig The color Response Surtace esign resolution:Green=Res V or higher,Yellow=Res IV,and Red=Res Ill. Factorial 因子设计 Number of Factors 5 2-Level Factorial☐ Min Run Res V Min Run Res IV 22 21 Ireqular Fraction General Factorial D-optimal 241 22 28 2 Plackett-Burman Taguchi OA 16 24 251 62 2 273 284 D95 2 106 5 2 61 32 2 8-3 9-4 2 10.5 26 9-3 10-4 64 128 27 2 92 103 Replicates: Blocks:1 Center points per block:门 Sovy Generators厂 Cancel Continue 图7-3(c)选择混料设计 C:\Documents and Settings\All Users\Documents\DX7 data\lyDesi Eile Edit Yiew Display Options Design Tools Help 回回多鱼宽 圖? 响应面设计 Response Surface Simplex Centroid Design 因子设计 Factorial Mixture design for 3 to 8 components where all components mu on the design space.The points chosen are the pure blends,b Combined centroid.By default,this design is augmented by adding check 混料设计 Mixture 料暖努界数he Total:1 Mixture Components: (3to) Units: 单纯形格子设计 Simplex Lattice 单纯形重心设计 Simplex Centroid Name Low High Screening D-最优设计 D-optimal A 0 7 Distance-Based 01 1 User-Defined Historical Data cc 0 1 D:D 鲁余筒卧毫鞋琴聚下界, 0 1 混料中4成分所占百分比 图7-3(d)选择重心设计、混料组成数、范围 -185-
- 185 - 图7-3(c) 选择混料设计 图7-3(d) 选择重心设计、混料组成数、范围