中国科学技术大学：《离散数学》课程教学资源（PPT课件讲稿）第二部分 集合论 第五章 函数

第五章函数 函数也叫映射，交换，是数学中的一个基本概念 在高数中，函数的概念是从变量的角度提出来的 这种函数一般是连续或间断连续的函数，这里将 连续函数的概念推广到离散量的讨论，即将函数 看作一种特殊的二元关系。 173

1/73 第五章 函数 函数也叫映射，交换，是数学中的一个基本概念， 在高数中，函数的概念是从变量的角度提出来的， 这种函数一般是连续或间断连续的函数，这里将 连续函数的概念推广到离散量的讨论，即将函数 看作一种特殊的二元关系

5.1函数的基本概念 定义5.，1：设f是集合A到B的关系，如果对每个x∈ A,都存在唯，一y∈B,,使得Ef,则称关系f 为A到B的函数(Funct ion),记为f:A+B。当∈f∧∈f→y=2； (4)|fl=|A; (5)f(x)仅表示一个变值，f表示一个集合，. f≠f(x) 2/73

2/73 5.1 函数的基本概念 • 定义5.1：设f是集合A到B的关系，如果对每个x A，都存在唯一y B，使得 f，则称关系f 为A到B的函数(Function)，记为f:A→B。当 f时，正常记为y=f(x)，x称为自变量，y为x 在f下的函数值。 (1)dom f=A，称为函数的定义域； (2)ran f B，称为函数的值域，ran f也可记为 f(A)，为A在f下的像； (3) ； (4)|f|=|A|； (5)f(x)仅表示一个变值，f表示一个集合， ∴       x, y  f   x,z  f  y = z f  f (x)

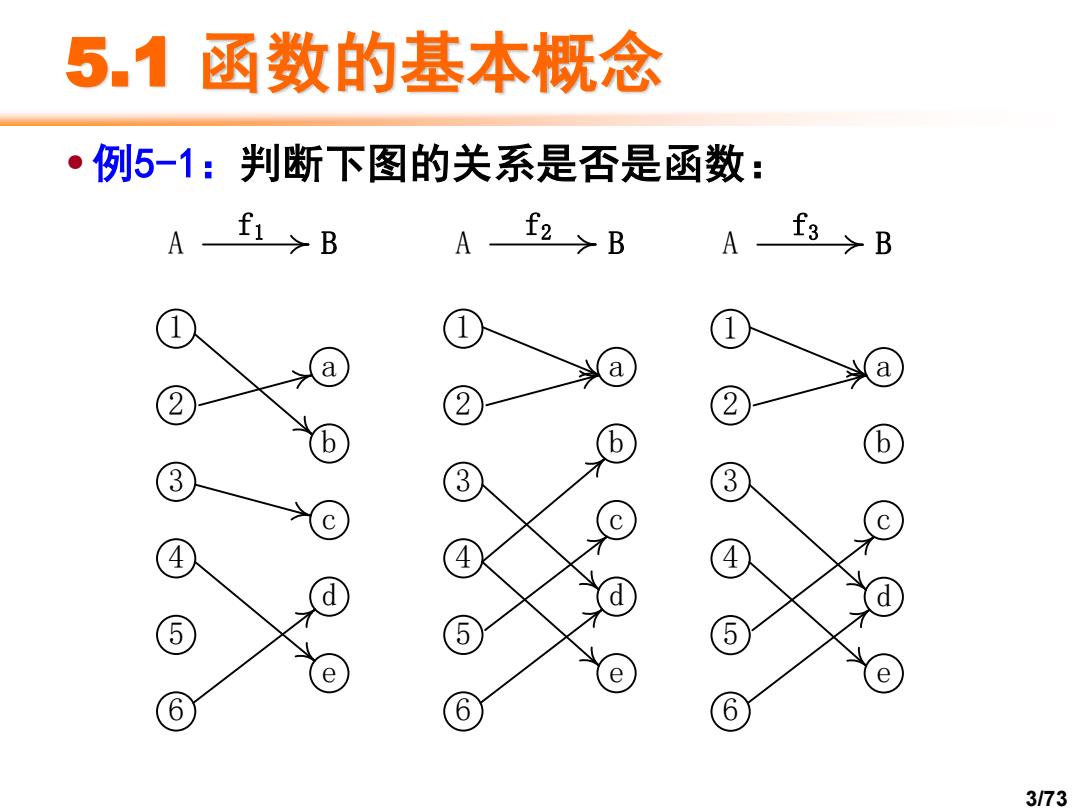
5.1函数的基本概念 例5-1：判断下图的关系是否是函数： A f1B A f2>B A a 2 3 5 e e 6 6 6 3/73

3/73 5.1 函数的基本概念 •例5-1：判断下图的关系是否是函数： 1 2 3 4 5 6 a b c d e A B f1 1 2 3 4 5 6 a b c d e A B f2 1 2 3 4 5 6 a b c d e A B f3

5.1函数的基本概念 例5-2：设A={a,b},B={1,2},则AXB={Ka,1>, ,,},此时A到B的不同关系有 16个；A到B的不同的函数有4个； f={,},f3={,}, f3={,},f4={,} ()AB的任何一个子集，都是A到B的关系，因此 从A到B的不同的关系有241个，但从A到B的不 同的函数却只有1BM个； ·(2)每个函数的基数为|A,但关系的基数可以为0 一直到AX B; 。(3)每个函数的第一个元素一定互不相同； ·(4)将A到B的一切函数构成的集合记为B={fIf:A→B; 4/73

4/73 5.1 函数的基本概念 •例5-2：设A={a，b}，B={1,2}，则A×B={， ，，}，此时A到B的不同关系有 16个；A到B的不同的函数有4个； • (1)A×B的任何一个子集，都是A到B的关系，因此 ，从A到B的不同的关系有 个，但从A到B的不 同的函数却只有 个； • (2)每个函数的基数为|A|，但关系的基数可以为0 一直到|A|×|B|； • (3)每个函数的第一个元素一定互不相同； • (4)将A到B的一切函数构成的集合记为 { ,2 , ,1 }, { ,2 , ,2 }. { ,1 , ,1 }, { ,1 , ,2 }, 3 4 1 2 =     =     =     =     f a b f a b f a b f a b | | | | 2 A B | | | | A B B { f | f : A B} A = →

5.2函数的性质 ·定义5.2：设f是从集合A到B的函数： (1)对x,x2∈A,若x≠x2,则f(x)≠f(x2),则称f为从A 到B的单射(Injection); (2)若ranf=B,则称f为A到B的满射(Sur jection); (3)若f既是单射，又是满射，则称f为从A到B的双射 (Bijection)或一一映射； (4)若A=B,则称f为A上的函数，当A上的函数f是双 射，称f为变换(Transform)。 >(1)f是单射的必要条件为|A≤B|,(2)f为满射 的必要条件为B|≤|A,(3)f为双射的必要条件 为A=B|。 5/73

5/73 5.2 函数的性质 •定义5.2：设f是从集合A到B的函数： (1)对 ，则称f为从A 到B的单射(Injection)； (2)若ran f=B，则称f为A到B的满射(Surjection); (3)若f既是单射，又是满射，则称f为从A到B的双射 (Bijection)或一一映射； (4)若A=B，则称f为A上的函数，当A上的函数f是双 射，称f为变换(Transform)。 ➢(1)f是单射的必要条件为|A|≤|B|，(2)f为满射 的必要条件为|B|≤|A|，(3)f为双射的必要条件 为|A|=|B|。 , , , ( ) ( ) 1 2 1 2 1 2 x x  A 若x  x 则f x  f x

5.2函数的性质 例5-3：确定下列关系哪些是函数，若是函数，是 否是单射，满射，双射。 (1)设A=B=R,f={x∈R),f2={x∈R, f3={kx,l/x>x∈R,f4={kx,e>lx∈R},f5={x∈R (2)A=R,B=R,f={xER). 解：(1)f:R到R的函数，：R到R的双射函数，f: 不是R到R的函数，f4:R到R的单射函数，f;:不是 R到R的函数； (2)f为R+到R的双射函数。 6/73

6/73 5.2 函数的性质 •例5-3：确定下列关系哪些是函数，若是函数，是 否是单射，满射，双射。 (1)设A=B=R， (2) 解：(1) ：R到R的函数， ：R到R的双射函数， ： 不是R到R的函数， ：R到R的单射函数， ：不是 R到R的函数； (2)f为 到R的双射函数。 { , | }, { , 1 | }, 2 2 f 1 =  x x  xR f =  x x +  xR { ,1/ | }, { , | }, { , | }. f 3 x x x R f 4 x e x R f 5 x x x R x =    =    =    A = R ,B = R, f ={ x,ln x | xR}. + 1 f 2 f 3 f 4 f 5 f + R

5.2函数的性质 例5-4：设是偏序集，对Va∈A,令f(a)= {x|x∈A∧x≤a},证()f是A到p(A)的单射函数 ,且(2)Ha,b∈A,a≤b则f(asf(b). 证明：（1)a∈A,f(a)={xlx∈AAx≤a}≤A,∴.f(a∈p(A) .f是A到p(A)的映射； Va,b∈A,a≠b :若a,b存在偏序关系，不妨设a ≤b,由于 66 ≤”是反对称的，：.ba,从而 b生f(a={x|x∈ANx≤a,而“≤”自反，.b ≤b,即b∈f(b)∴.f(a)≠f(b) 773

7/73 5.2 函数的性质 •例5-4：设是偏序集，对 ，证(1)f是A到ρ(A)的单射函数 ，且(2) 证明：(1) ∴f是A到ρ(A)的映射； ①：若a，b存在偏序关系，不妨设a ≤b，由于 “≤”是反对称的， ，从而 ，而“≤”自反， ∴ b ≤b，即 a A,令f (a) = {x | x A x  a} a,b A,a  b则f (a)  f (b)。 a A, f (a) ={x | x A x  a} A, f (a) (A) a,b A,a  b b  a b f (a) ={x | x A x  a} b f (b) f (a)  f (b)

5.2函数的性质 ②若a,b不存在偏序关系，则ab,从而 a生f(b)={x|x∈AAx≤b},而“≤”自反，即 a∈f(a∴.f(a)≠f(b) .f是A到p(A)的单射； (2)Va,b∈A,若a≤b,任取y∈f(a),则y≤a,而a≤b 由传递性，有y≤b,∴.y∈f(b),∴.f(asf(b) 定理5.1：设A,B是有限集合，且A=B,f是A 到B的函数，则f是单射当且仅当f是满射。 8/73

8/73 5.2 函数的性质 ②若a，b不存在偏序关系，则 ，从而 ，而“≤”自反，即 ∴f是A到ρ(A)的单射； (2) 由传递性，有y ≤b, • 定理5.1：设A，B是有限集合，且|A|=|B|，f是A 到B的函数，则f是单射当且仅当f是满射。 a  b a f (b) ={x | x A x  b} a f (a) f (a)  f (b) a,b A,若a  b，任取y f (a)，则y  a，而a  b  y  f (b), f (a)  f (b)

5.2函数的性质 证明：必要性：设f是单射，f是A到f(A)的满射， .f是A到f(A)的双射，因此A=f(A)|,由于| f(A)|=|B,且f(A)∈B,得f(A)=B, .f是A到B的满射； 充分性：设f是满射，x,x2∈A,x1≠x2,若f(x)=f(x2) 由于f是A到B的满射，∴.f也是A-{x}到B的满射，故 |A-{x}≥B,即川A-1B|,矛盾.f(x)≠f(x2) 即f是A到B的单射。 9/73

9/73 5.2 函数的性质 证明：必要性：设f是单射，f是A到f(A)的满射， ∴f是A到f(A)的双射，因此|A|=|f(A)|，由于| f(A)|=|B|，且 ，得f(A)=B， ∴f是A到B的满射； 充分性：设f是满射， 由于f是A到B的满射，∴f也是 到B的满射，故 即f是A到B的单射。 f (A)  B , , , ( ) ( ) 1 2 1 2 1 2 x x  A x  x 若f x = f x { }1 A− x | { }| | |, | | 1 | | ( ) ( ) 1 1 2 A− x  B 即 A −  B ，矛盾 f x  f x

5.3函数的复合运算 定义5.3：常函数，恒等函数，单调函数，特征函 数，自然映射。 定理5.2：设F，G是函数，则FoG也是函数，且满 足：（1)dom(FoG)={x|x∈domF∧F(x)∈domG (2)Vx∈dom(FoG)有FoG=G(F(x) 证明：(1)Hx,x∈dom(FoG)→3妇y(∈F∧∈G) →3t(x∈domF∧t=F(x)∧t∈domG) →x∈{x|x∈domFF(x)∈domG} (2)Vx,x∈domF∧F(x)∈domG →∈F∧∈G→∈FoG →x∈domFoG∧FoG(x)=G(F(x) 10/73

10/73 5.3 函数的复合运算 •定义5.3：常函数，恒等函数，单调函数，特征函 数，自然映射。 •定理5.2：设F，G是函数，则FοG也是函数，且满 足：(1) (2) dom(F G) ={x | xdomF  F(x)domG} xdom(F G)有F G = G(F(x)) ( ) ( ( )) , ( ) ( ), ( ( )) , ( ( )) (2) , ( ) { | ( ) } ( ( ) ) (1) , ( ) ( , , ) x domF G F G x G F x x F x F F x G F x G x G F x F G x x domF F x domG x x x domF F x domG t x domF t F x t domG x x dom F G t y x t F t y G    =                          =                  证明： 