
中国学我术大草 University of Science and Technology of China GAMES102在线课程:几何建模与处理基础 细分曲线
细分曲线 GAMES 102在线课程:几何建模与处理基础
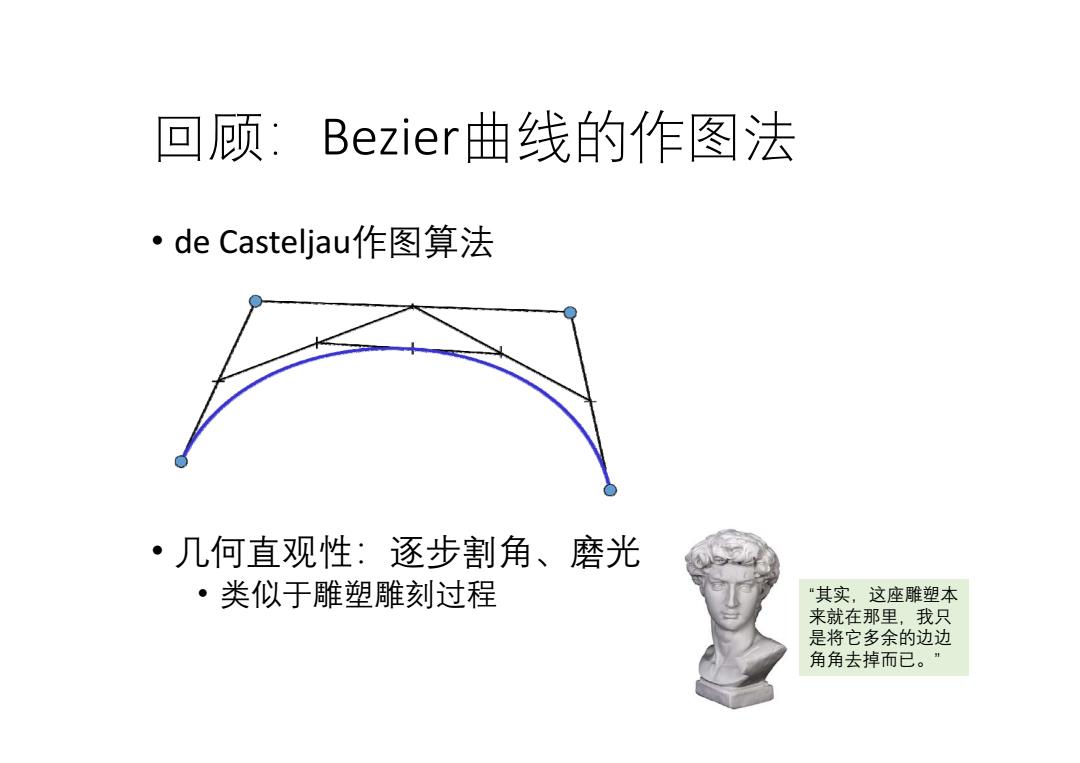
回顾:Bezier曲线的作图法 ·de Casteljau作图算法 ·几何直观性:逐步割角、磨光 ·类似于雕塑雕刻过程 “其实,这座雕塑本 来就在那里,我只 是将它多余的边边 角角去掉而已
回顾:Bezier曲线的作图法 • de Casteljau作图算法 • 几何直观性:逐步割角、磨光 • 类似于雕塑雕刻过程 “其实,这座雕塑本 来就在那里,我只 是将它多余的边边 角角去掉而已

问题 ·输入:一个简单多边形(控制多边形) ·输出:一条与之关联的光滑曲线
问题 • 输入:一个简单多边形(控制多边形) • 输出:一条与之关联的光滑曲线
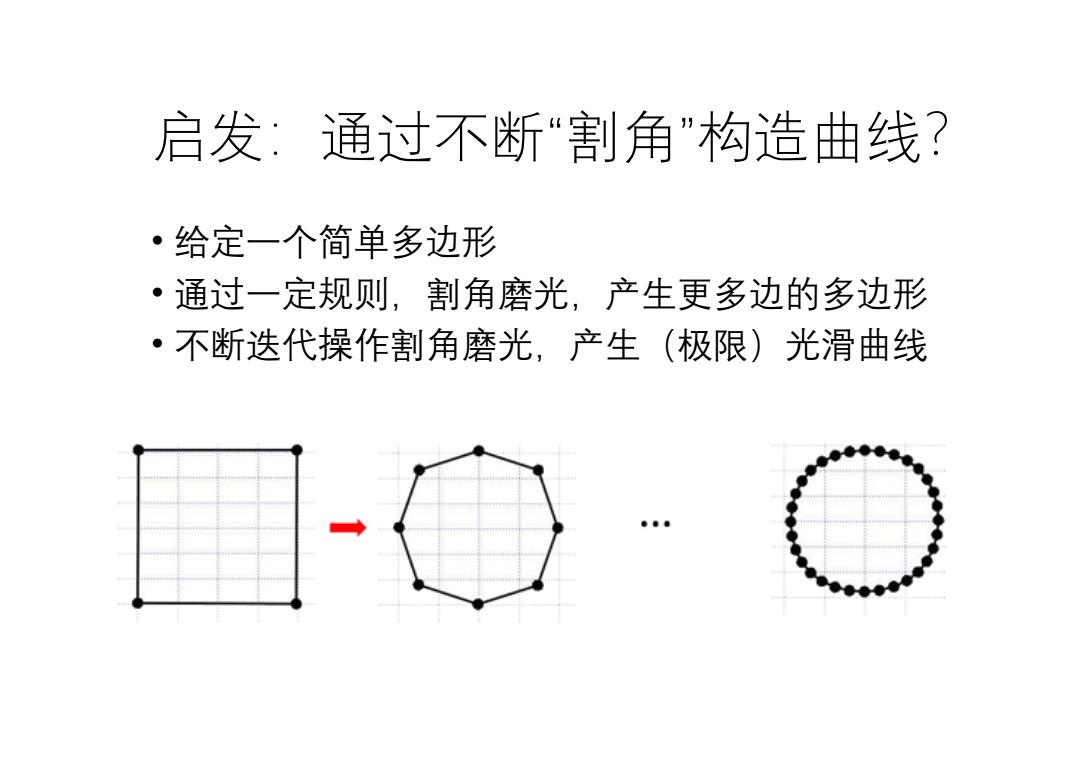
启发:通过不断“割角”构造曲线? ·给定一个简单多边形 ·通过一定规则,割角磨光,产生更多边的多边形 ·不断迭代操作割角磨光,产生(极限)光滑曲线
启发:通过不断“割角”构造曲线? • 给定一个简单多边形 • 通过一定规则,割角磨光,产生更多边的多边形 • 不断迭代操作割角磨光,产生(极限)光滑曲线
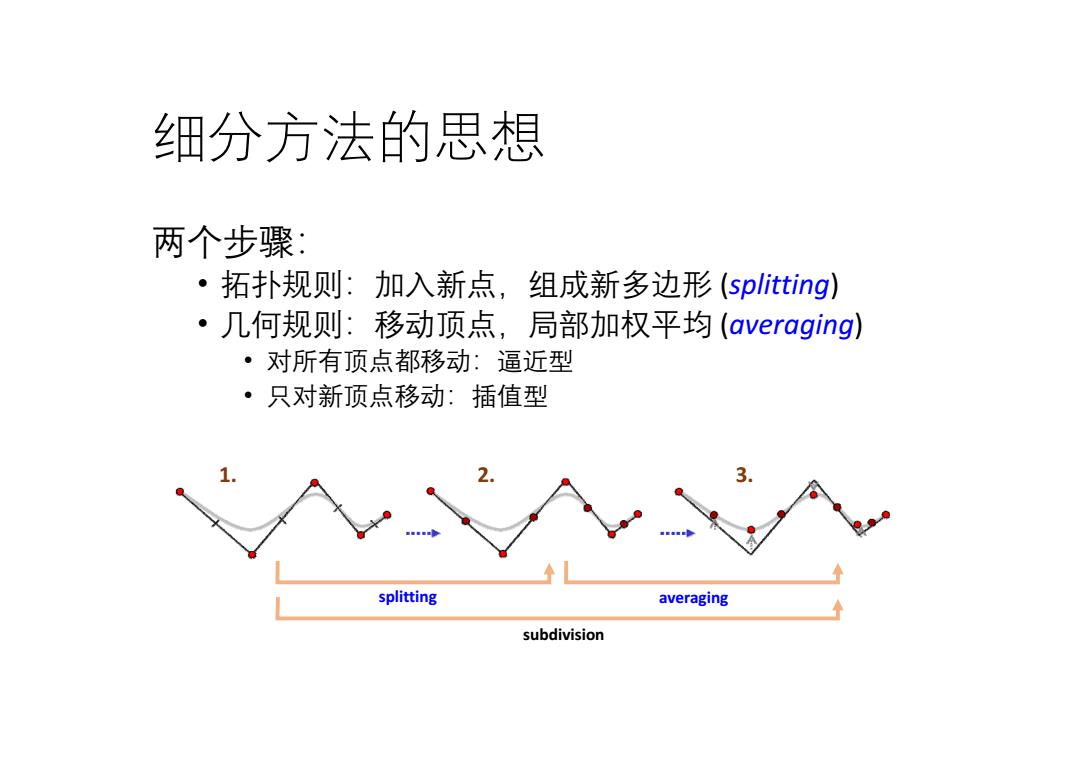
细分方法的思想 两个步骤: ·拓扑规则:加入新点,组成新多边形(splitting) ·几何规则:移动顶点,局部加权平均(averaging) ·对所有顶点都移动:逼近型 ·只对新顶点移动:插值型 splitting averaging subdivision
细分方法的思想 两个步骤: • 拓扑规则:加入新点,组成新多边形 (splitting) • 几何规则:移动顶点,局部加权平均 (averaging) • 对所有顶点都移动:逼近型 • 只对新顶点移动:插值型 1. 2. 3. splitting averaging subdivision

Chaikin细分方法
Chaikin细分方法
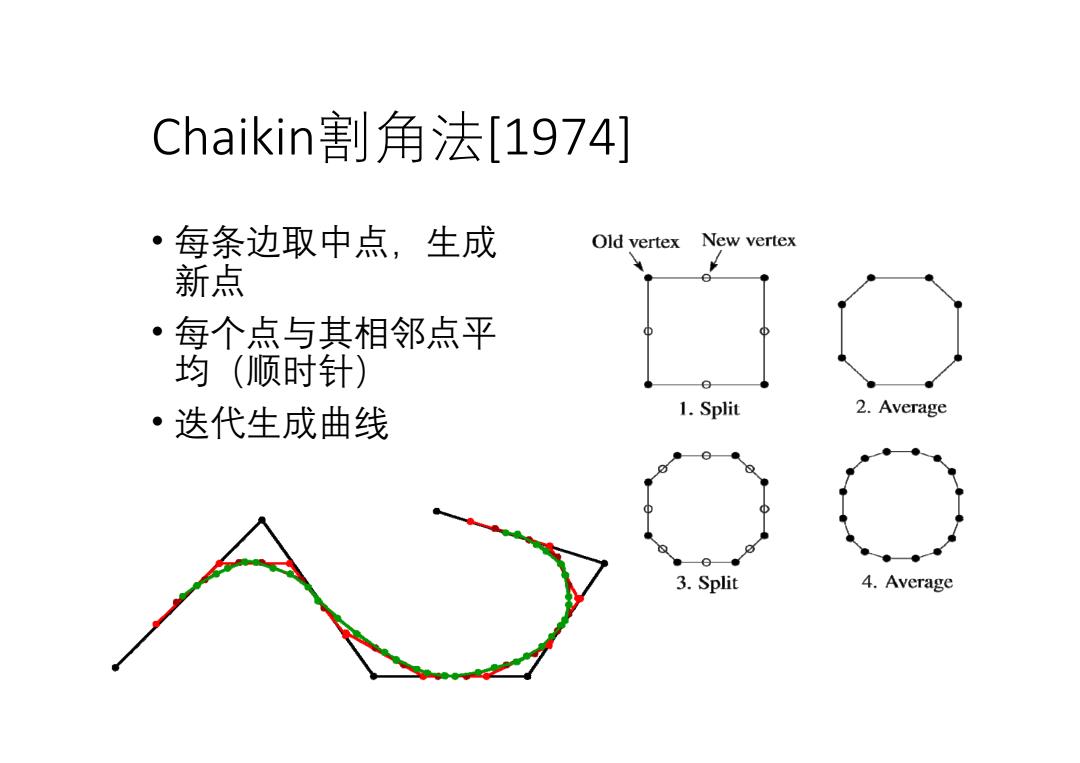
Chaikin割角法[1974] ·每条边取中点,生成 Old vertex New vertex 新点 ·每个点与其相邻点平 均(顺时针) ·迭代生成曲线 1.Split 2.Average 3.Split 4.Average
Chaikin割角法[1974] • 每条边取中点,生成 新点 • 每个点与其相邻点平 均(顺时针) • 迭代生成曲线
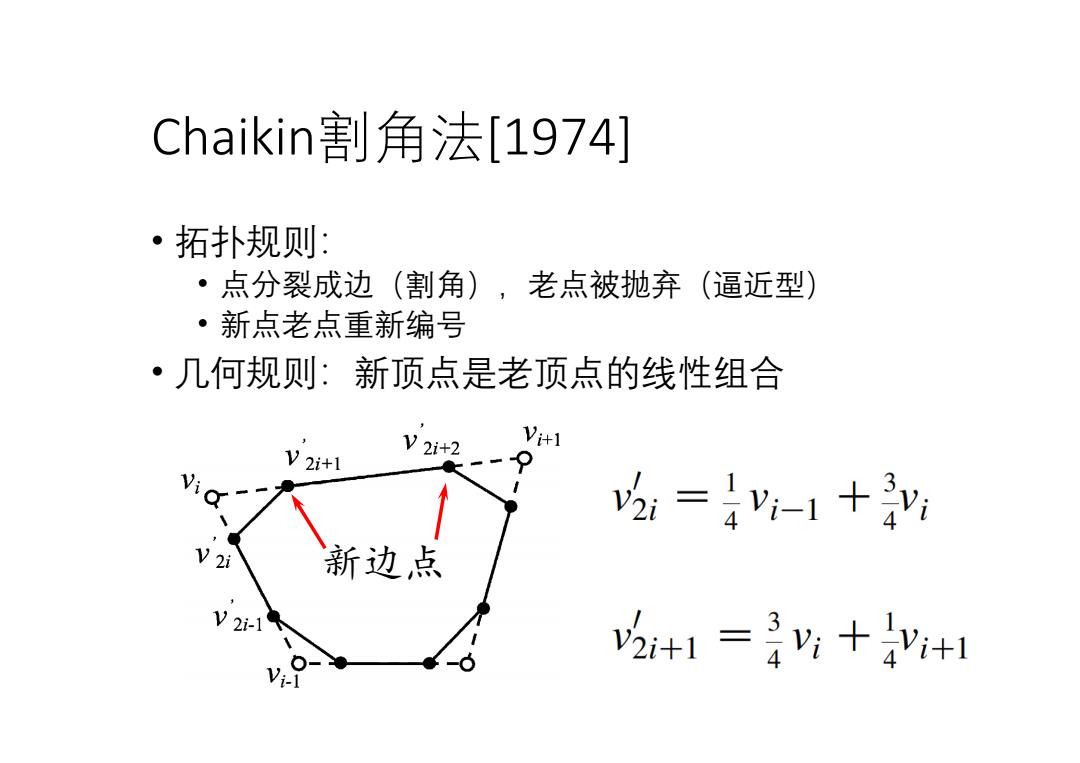
Chaikin割角法[1974] ·拓扑规则: ·点分裂成边(割角),老点被抛弃 (逼近型) ·新点老点重新编号 ·几何规则:新顶点是老顶点的线性组合 V2i+1 V2i+2 V+1 -9 2:=4-1+ V 2i 新边点 V2i-1 2+1=+4y+1
Chaikin割角法[1974] • 拓扑规则: • 点分裂成边(割角),老点被抛弃(逼近型) • 新点老点重新编号 • 几何规则:新顶点是老顶点的线性组合 新边点
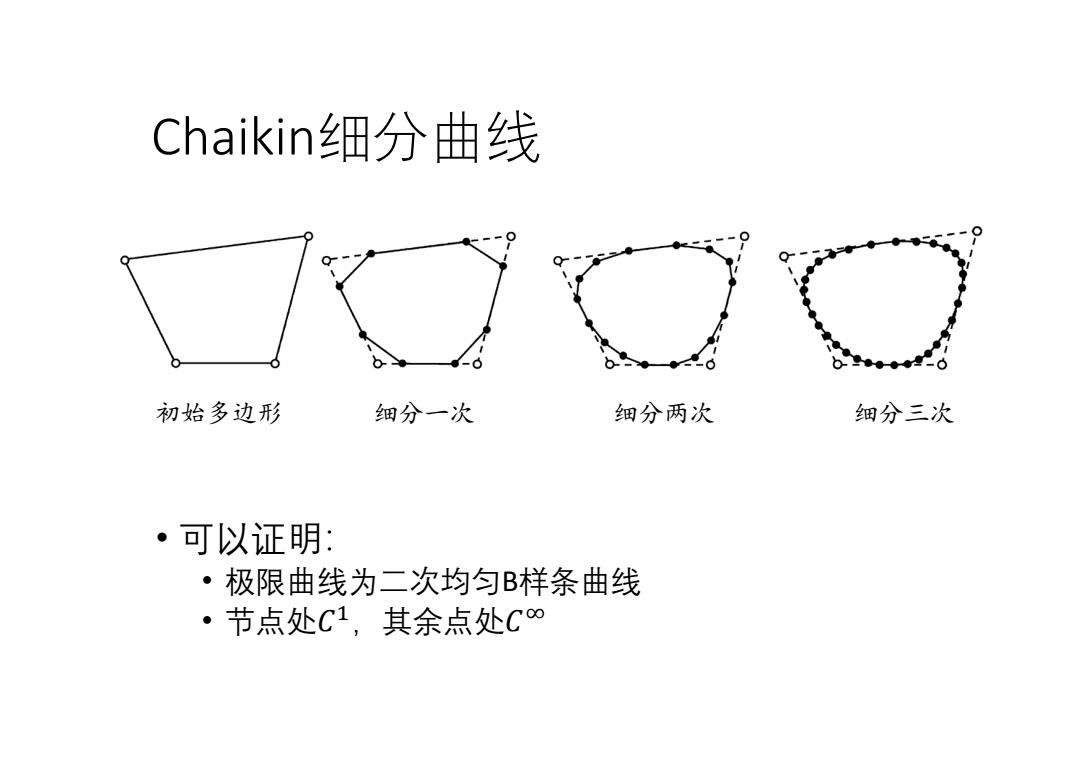
Chaikin细分曲线 初始多边形 细分一次 细分两次 细分三次 。可以证明: ·极限曲线为二次均匀B样条曲线 ·节点处C1,其余点处C∞
Chaikin细分曲线 • 可以证明: • 极限曲线为二次均匀B样条曲线 • 节点处𝐶ଵ,其余点处𝐶ஶ 初始多边形 细分一次 细分两次 细分三次
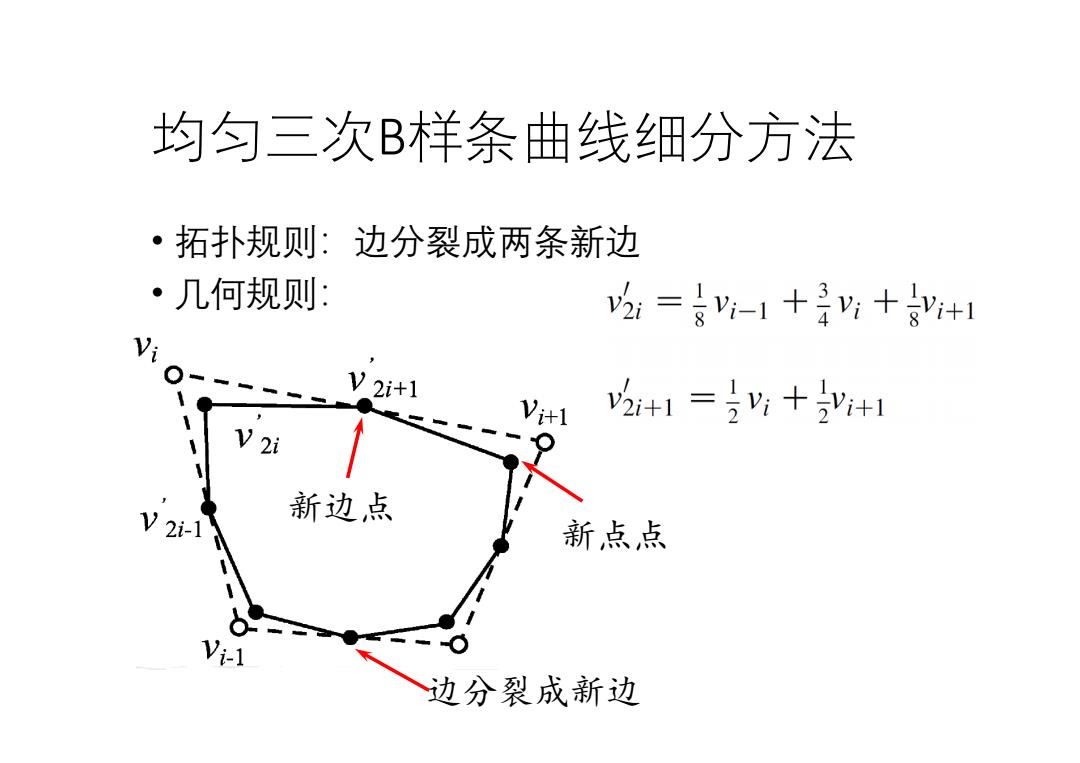
均匀三次B祥条曲线细分方法 ·拓扑规则:边分裂成两条新边 ·几何规则: 2=8y-1+:+gy+1 Vi V2i计1 V+1 2+1=)V?++1 V2i V2i-1 新边点 新点点 边分裂成新边
均匀三次B样条曲线细分方法 • 拓扑规则:边分裂成两条新边 • 几何规则: 边分裂成新边 新点点 新边点