
高等数学教案 第一章函数与极限 第三节函数的极限 教学内容:函数极限定义以及性质。 教学目标:使学生建立起函数极限的准确概念:会用函数极限的定义证明函数极限等有 关命题。 教学重点:函数极限的概念 教学难点:函数极限的ε-6定义及其应用 教学方法:新课讲授法 作业:p381,2,3,4. 教学过程: 一、函数极限的定义 函数的自变量有儿种不同的变化趋势: x无限接近x0:x→x0, x从xo的左侧(即小于xo)无限接近x0:x→x0, x从和的右侧(即大于xo)无限接近x0:xxo, x的绝对值无限增大:x→0, x小于零且绝对值无限增大:x→0, x大于零且绝对值无限增大:x→+o. 1.自变量趋于有限值时函数的极限 通俗定义: 如果当x无限接近于x0,函数)的值无限接近于常数A,则称当x趋于xo时,x)以A为极 限.记作 limx)=A或fx)→A(当x→xo)为 分析:在xxo的过程中,x)无限接近于A就是x少A能任意小,或者说,在x与xo接近到 一定程度(比如-x水6δ为某一正数)时,x)-A可以小于任意给定的(小的)正数,即 x)-AkE.反之,对于任意给定的正数£,如果x与接近到一定程度(比如-xk66为某 一正数)就有x)Aε,则能保证当xxo时,x)无限接近于A. 定义1设函数x)在点的某一去心邻域内有定义.如果存在常数A,对于任意给定的正数 ε(不论它多么小),总存在正数6使得当x满足不等式0<-x水kδ时,对应的函数值x)都满 足不等式x)-A<ε

高等数学教案 第一章函数与极限 那么常数A就叫做函数x)当xxo时的极限,记为 limf(x)=A或fx)>A(当xxo). x→n 定义的简单表述: l1imf(x)=A→>0,30,当00,可任取0,当00,要使x)-Ake,只要r-xdkE. 证明:因为Ve>0,38=6,当00,要使A水G,只婴x-号 证明:因为ve>0,3G628-号,当0-1k6时,有4(2x-1少-1=2-1ke 所以1im(2x-)=1. 2 例4.证明1im x2-1 分析:注意函数在x=1是没有定义的,但这与函数在该点是否有极限并无关系 当1陈,4小H2ve>0医使水e,只要-ke 证明因为ve>0,,当0-k6时,有4小告本-1c, 所以1im2- =2 1x-1 三、单侧极限: 2

高等数学教案 第一章函数与极限 若当xxo时,x)无限接近于某常数A,则常数A叫做函数x)当xxo时的左极限,记为 1imf(x)=A或xo)=A; x→a 若当xx时,x)无限接近于某常数A,则常数A叫做函数x)当xxo时的右极限,记为 limf(x)=A或x,)=A. 个1 x-.xo 讨论:1.左右极限的£-6定义如何叙述? 2.当xxo时函数x)的左右极限与当xxo =x+1 时函数x)的极限之间的关系怎样? 提示:左极限的E-6定义: lim f(x)=AV6>0,36>0,Vx:xo-&x0,38>0,x:xo0 这是因为, i/)=lim(x-1)--1. lim f(x)=lim (x+1)=1, ¥0+ x0+ limf(x)≠limf(x). X0- x0t 四、自变量趋于无穷大时函数的极限 设x)当x大于某一正数时有定义.如果存在常数A,对于任意给定的正数E,总存在着正数 X,使得当x满足不等式xPX时,对应的函数数值x)都满足不等式 f(x)-A<s 则常数A叫做函数x)当x→o时的极限,记为 limf(x)=A或x)→A(x→o). N》买 3
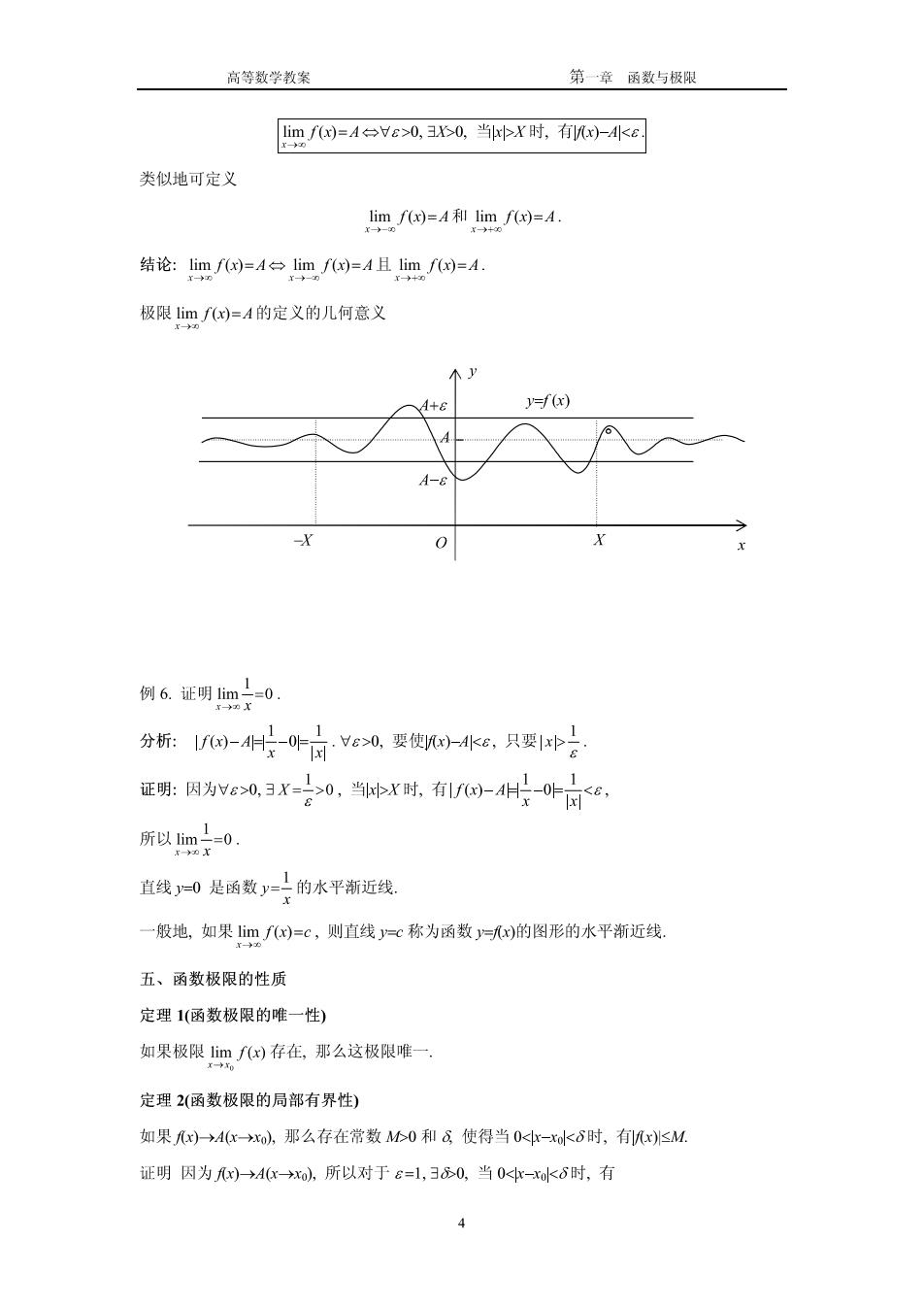
高等数学教案 第一章函数与极限 lim f(x)=A台Ve>0,3X0,当X时,有x)-<& 类似地可定义 lim f(x)=4 lim f(x)=4. N)+00 结论:limf(x)=A台lim f(x)=A且limf()=A. 十 极限limf(x)=A的定义的几何意义 0 A+6 y=f(x) A-8 X 例6.证明1im1=0 分折:4H司Y0医使水c,只中号 正明:因为N8x合0,当冲X时,有-付-8, 所以im上=0. xx 直线=0是函数y}的水平渐近线 一般地,如果Iimf(x)=c,则直线y=c称为函数=x)的图形的水平渐近线. 五、函数极限的性质 定理1(函数极限的唯一性) 如果极限imf(x)存在,那么这极限唯一. 定理2(函数极限的局部有界性) 如果x)→A(cxo),那么存在常数0和6使得当0<本-xdk6时,有x)≤M. 证明因为x)→Axxo),所以对于&=1,30,当0<本-xk6时,有 4

高等数学教案 第一章函数与极限 x)-A0(或A0(或 fx)0的情形证明. 因为mf=A,所以对于6=,36>0,当04-水8时,有 -4水6=号4fe-号0 定理3 如果)--040,那么存在点n的某一去心邻域,在该邻域内,有fpA利。 推论如果在的某一去心邻域内x)≥0(或x)s0),而且x)→Ax→xo),那么A≥0(或A≤0). 证明:设fx)≥0.假设上述论断不成立,即设A0,38>0,当00,3VeN,当>N时,有xw-xdk6. 由假设,xn≠xo(n∈N.故当>N时,0<m一xk6,从而x)-A<e,即 lim f(x)=lim f(x) 》x 5